代码随想录 NO52 | 动态规划_leetcode 647. 回文子串 516.最长回文子序列
动态规划_leetcode 647. 回文子串 516.最长回文子序列
今天是动态规划最后一天的题了,整个过程已经接近尾声了!
647. 回文子串

-
确定dp数组(dp table)以及下标的含义
本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
在判断字符串S是否是回文,那么如果知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。 -
确定递推公式
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。- 当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
- 当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
if s[i] == s[j]:if j - i <= 1:result += 1dp[i][j] = Trueelif dp[i + 1][j - 1]:result += 1dp[i][j] = True
-
dp数组如何初始化
dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹配上了。
所以dp[i][j]初始化为false。 -
确定遍历顺序
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:

所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。 -
举例推导dp数组

class Solution:def countSubstrings(self, s: str) -> int:dp = [[False] * len(s) for _ in range(len(s))]result = 0for i in range(len(s)-1, -1, -1): #注意遍历顺序for j in range(i, len(s)):if s[i] == s[j]:if j - i <= 1: #情况一 和 情况二result += 1dp[i][j] = Trueelif dp[i+1][j-1]: #情况三result += 1dp[i][j] = Truereturn result
516.最长回文子序列

- 确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。 - 确定递推公式
- 在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2; - 如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
- 在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
- dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。 - 确定遍历顺序
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:

所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。 - 举例推导dp数组

class Solution:def longestPalindromeSubseq(self, s: str) -> int:dp = [[0 for _ in range(len(s))] for _ in range(len(s))]for i in range(len(s)):dp[i][i] = 1for i in range(len(s)-1,-1,-1):for j in range(i+1,len(s)):if s[i] == s[j]:dp[i][j] = dp[i+1][j-1] +2else:dp[i][j] = max(dp[i][j-1], dp[i+1][j])return dp[0][-1]
今天这两道题还挺绕的,第一题数组定义不能再根据以往经验来以最后一个字符为限,另外遍历顺序也有所不同!
相关文章:

代码随想录 NO52 | 动态规划_leetcode 647. 回文子串 516.最长回文子序列
动态规划_leetcode 647. 回文子串 516.最长回文子序列今天是动态规划最后一天的题了,整个过程已经接近尾声了! 647. 回文子串 确定dp数组(dp table)以及下标的含义 本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp…...
【数据挖掘】1、综述:背景、数据的特征、数据挖掘的六大应用方向、有趣的案例
目录一、背景1.1 学习资料1.2 数据的特征1.3 数据挖掘的应用案例1.4 获取数据集1.5 数据挖掘的定义二、分类三、聚类四、关联分析五、回归六、可视化七、数据预处理八、有趣的案例8.1 隐私保护8.2 云计算的弹性资源8.3 并行计算九、总结一、背景 1.1 学习资料 推荐书籍如下&a…...
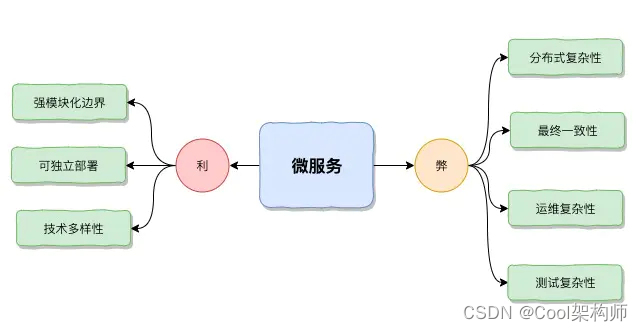
【架构师】零基础到精通——康威定律
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...

Could not extract response: no suitable HttpMessageConverter
版本:spring-cloud-openfeign-core-2.1.1.RELEASE.jar,spring-webmvc-5.1.14.RELEASE.jar,jetty-server-9.4.41.v20210516.jar,tomcat-embed-core-9.0.48.jar 问题背景 生产服务请求下游服务时偶发抛出下面的异常,下…...

文献计量三大定律之一---洛特卡定律及普赖斯定律
科学生产率是洛特卡定律的基础,科学生产率”(Scientific Productivity))是指科学家(科研人员)在科学上所表现出的能力和工作效率,通常用其生产的科学文献的数量来衡量。 1926年,洛特卡在一篇论文中提出了科…...
2023年软考高级网络规划设计师
网络规划设计师是软考高级考试科目之一,也是比较难的科目,据官方数据统计网规每年的通过率很低,而且每年只有下半年11月份考一次,如果是直接裸考,估计很悬哦~ 但是你参加考试获得证书的过程就是一个学习网络规划系统知…...

数据治理驱动因素 -报考题
数据治理并不是到此为止,而是需要直接与企业战略保持一致。数据治理越显著地帮助解决组织问题,人们越有可能改变行为、接受数据治理实践。数据治理的驱动因素大多聚焦于减少风险或者改进流程。(1)减少风险1)一般性风险…...
2023淘宝天猫38节红包满减优惠活动时间是从几月几号什么时候开始?
2023年淘宝天猫38节活动将于2023年3月2日中午12点正式开始,活动将持续至2023年3月8日晚上23点59分。届时,淘宝天猫将推出一系列的优惠活动和红包福利,为广大女性用户送上节日的祝福和福利。在这个特别的节日里,淘宝天猫为女性用户…...
、数据压缩、存储优化)
Hive表优化、表设计优化、Hive表数据优化(ORC)、数据压缩、存储优化
文章目录Hive表优化Hive表设计优化分区表结构 - 分区设计思想分桶表结构 - Join问题Hive中的索引Hive表数据优化常见文件格式TextFileSequenceFileParquetORC数据压缩存储优化 - 避免小文件生成存储优化 - 合并输入的小文件存储优化 - ORC文件索引Row Group IndexBloom Filter …...

LearnOpenGL-入门-着色器
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject LearnOpenGL中文官网:https://learnopengl-cn.github.io/ 文章目录着色器GLSL数据类型输入与输…...
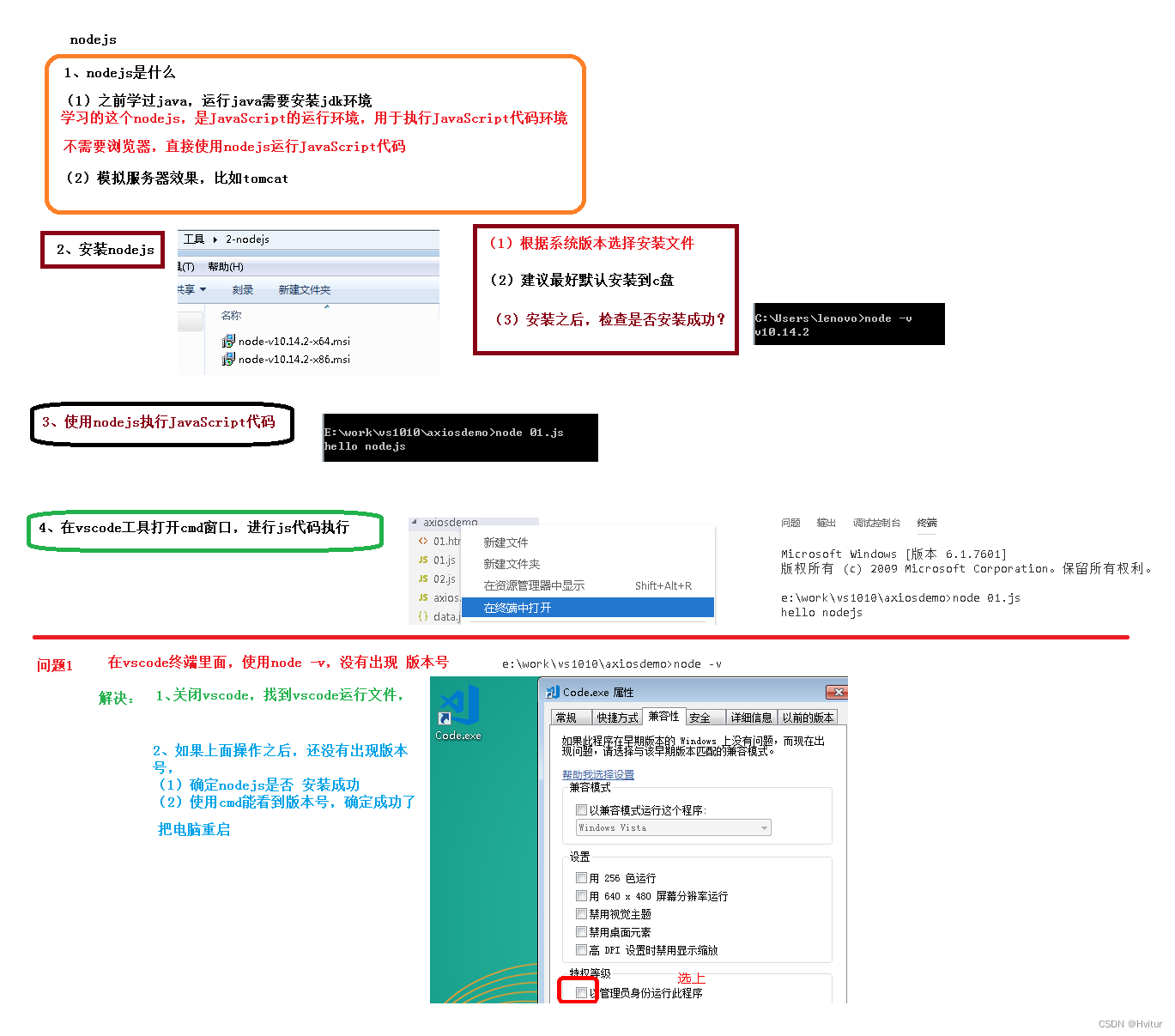
【谷粒学院】vue、axios、element-ui、node.js(44~58)
44.前端技术-vue入门 🧨Vue.js 是什么 Vue (读音 /vjuː/,类似于 view) 是一套用于构建用户界面的渐进式框架。 Vue 的核心库只关注视图层,不仅易于上手,还便于与第三方库或既有项目整合。另一方面,当与现代化的工具…...

【一些回忆】2022.02.26-2023.02.26 一个普通男孩的365天
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:一些回忆 为什么选择在这个时间节点回忆一下呢? 一是因为今天距离2023高考仅剩1…...
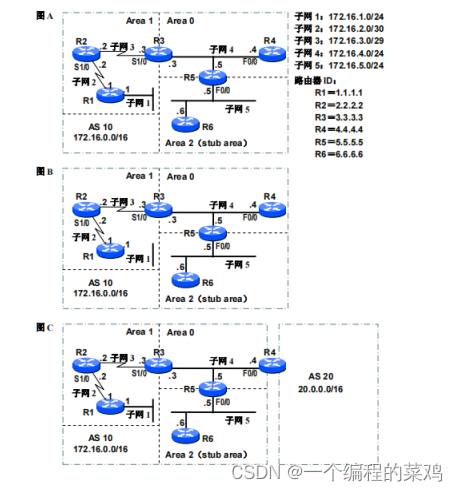
OSPF的多区域特性 (电子科技大学TCP/IP实验三)
一.实验目的 1、掌握OSPF 协议中区域的类型、特征和作用 2、掌握OSPF 路由器的类型、特征和作用 3、掌握OSPF LSA 分组的类型、特征和作用 4、理解OSPF 区域类型、路由器类型和OSPF LSA 分组类型间的相互关系 二.预备知识 1、静态路由选择和动态路…...
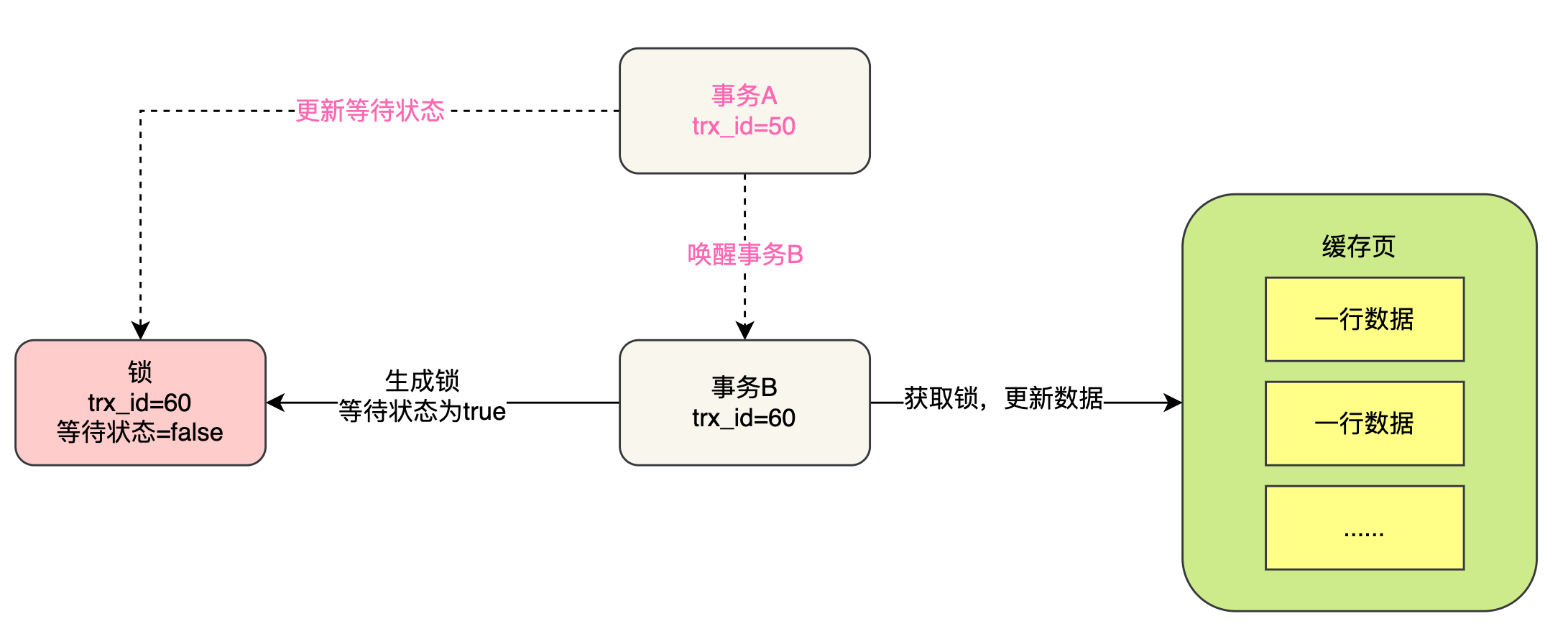
(四十四)多个事务更新同一行数据时,是如何加锁避免脏写的?
之前我们已经用很多篇幅给大家讲解了多个事务并发运行的时候,如果同时要读写一批数据,此时读和写时间的关系是如何协调的,毕竟要是你不协调好的话,可能就会有脏读、不可重复读、幻读等一系列的问题。 简单来说,脏读、…...

【数据库】第十二章 数据库管理
第12章 数据库管理 数据库的物理存储 关于内存、外存、磁盘、硬盘、软盘、光盘的区别_Allenzyg的博客-CSDN博客_磁盘和硬盘的区别 数据库记录在磁盘上的存储 定长,变长跨块,非跨快 文件的组织方方法: 无序记录文件(堆文件heap或pile file…...
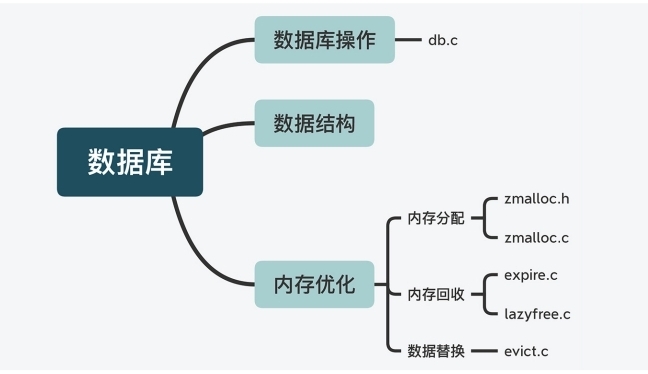
Redis源码---整体架构
目录 前言 Redis目录结构 前言 deps目录 src 目录 tests 目录 utils 目录 重要的配置文件 Redis 功能模块与源码对应 前言 服务器实例 数据库数据类型与操作 高可靠性和高可扩展性 辅助功能 前言 以先面后点的方法推进无特殊说明,都是基于 Redis 5.0.…...
基于springboot+vue的校园招聘系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...
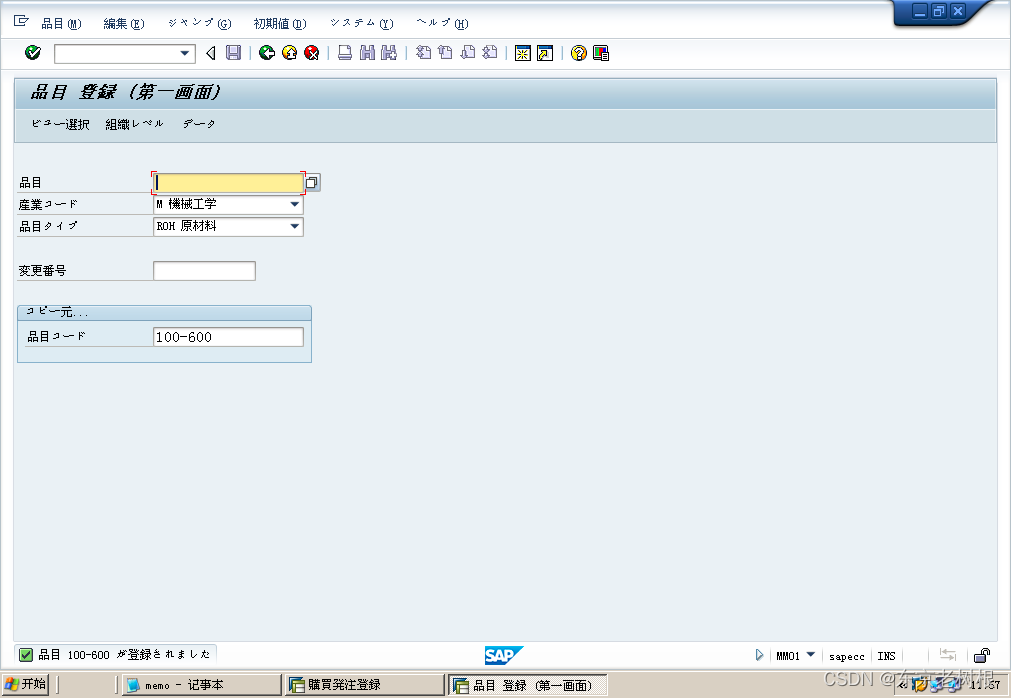
SAP MM学习笔记1-SAP中扩张的概念,如何将一个物料从工厂A扩张到工厂B
MM中在创建物料的时候,最低也得创建如下5个view。 基本数据1 基本数据2 购买管理 会计1 会计2 1,扩张是什么 有时候,你想增加其他的View,比如保管场所 等,你不能用MM02来做编辑,要用MM01来做扩张。这就是扩…...
【Python】Numpy数组的切片、索引详解:取数组的特定行列
【Python】Numpy数组的切片、索引详解:取数组的特定行列 文章目录【Python】Numpy数组的切片、索引详解:取数组的特定行列1. 介绍2. 切片索引2.1 切片索引先验知识2.1 一维数组的切片索引2.3 多维数组的切片索引3. 数组索引(副本)…...

2023年全国最新交安安全员精选真题及答案6
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 51.安全生产资金保障制度建立后关键在于落实,各施工企业在落实安全生…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
