当前位置： 首页 > news >正文

Ensemble Methods集成学习大比拼：性能、应用场景和可视化对比总结

news 2026/2/8 0:01:04

集成学习（Ensemble Learning）是一种机器学习范式，其中多个模型（通常称为“弱学习器”）被训练以解决相同的问题，并且通过某种方式结合它们的预测以提高整体性能。这种方法的核心思想是，多个模型比单一模型更能准确地预测未知数据。在本文中，我们将探讨多种集成学习算法，并从性能、应用场景、数据可视化选择、优缺点和性能评估等多个方面进行对比。

这种方法的核心思想是，多个模型的集合通常比单一模型更能准确地预测未知数据。这种方法在各种应用中都有广泛的应用，从自然语言处理和图像识别到金融风险评估和医疗诊断。本文旨在深入探讨各种集成学习算法，包括但不限于HistGradientBoostingClassifier、RandomForestRegressor和AdaBoostClassifier等。通过从性能、应用场景、数据可视化选择、优缺点和性能评估等多个方面进行全面的比较，本文将为读者提供一个全面的视图，以便根据具体的应用需求和限制来选择最适合的模型。

文章目录

  • 性能对比
  • 应用场景对比
  • 数据可视化选择
  • 优缺点对比
  • 性能评估
  • sklearn零基础入门
  • 结论

性能对比

在性能方面，HistGradientBoosting系列算法在训练和预测速度上都表现出色，准确性也很高，但在可扩展性和内存消耗方面表现一般。Voting系列算法在各方

相关文章：

Ensemble Methods集成学习大比拼：性能、应用场景和可视化对比总结

集成学习（Ensemble Learning）是一种机器学习范式，其中多个模型（通常称为“弱学习器”）被训练以解决相同的问题，并且通过某种方式结合它们的预测以提高整体性能。这种方法的核心思想是，多个模型比单一模型更能准确地预测未知数据。在本文中，我们将探讨多种集成学习算法，…...

编程日记 2023/10/29 10:09:31

【2024秋招】2023-9-16 贝壳后端开发二面

1 自我介绍 2 秒杀系统 2.1 超卖怎么解决 3 redis 3.1 过期策略 3.2 过期算法 4 kafka 4.1 说一说你对kafka的了解 4.2 如何保证事务性消息 4.3 如何保证消息不丢失 4.4 消息队列的两种通信方式 点对点模式 如上图所示，点对点模式通常是基于拉取或者轮询…...

编程日记 2023/10/29 10:07:29

SpringCloud 微服务全栈体系（七）

第九章 Docker 一、什么是 Docker 微服务虽然具备各种各样的优势，但服务的拆分通用给部署带来了很大的麻烦。 分布式系统中，依赖的组件非常多，不同组件之间部署时往往会产生一些冲突。在数百上千台服务中重复部署，环境不一定一致…...

编程日记 2023/10/29 10:06:27

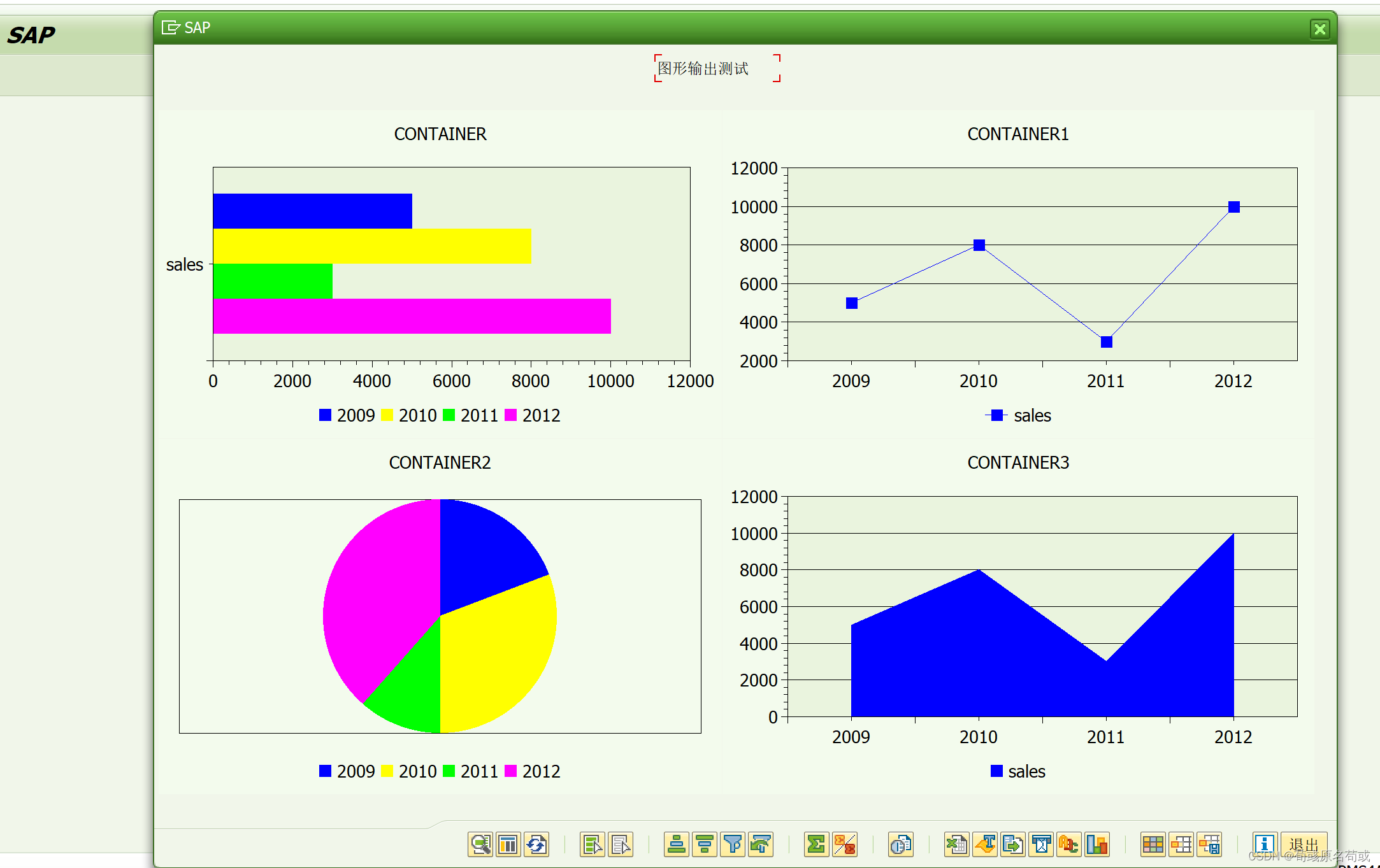
SAP ABAP 报表输出成 excel 统计图形 （RFC : GFW_PRES_SHOW_MULT）

SAP 预设了一个类型组 GFW ，做简单的excel图形输出 话不多说，直接上代码： *&---------------------------------------------------------------------* *& Report ZCYCLE057 *&----------------------------------------------…...

编程日记 2023/10/29 10:05:26

微信小程序如何获取地理位置

在微信小程序中，可以通过以下步骤获取用户的地理位置： 在小程序的app.json文件中配置权限： json "permission": {"scope.userLocation": {"desc": "你的位置信息将用于获取附近的服务"} }这样配置后…...

编程日记 2023/10/29 10:04:25

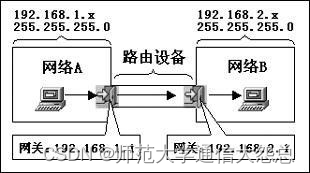
计算机网络相关硬件介绍

计算机相关硬件 计算机由运算器、控制器、存储器、输入设备和输出设备等五个逻辑计算机硬件部件组成。 一、中央处理器（CPU）（运算器、控制器） （1）运算器 运算器是对数据进行加工处理的部件&#xff…...

编程日记 2023/10/29 10:02:21

Megatron-LM GPT 源码分析（三） Pipeline Parallel分析

引言 本文接着上一篇【Megatron-LM GPT 源码分析（二） Sequence Parallel分析】，基于开源代码 GitHub - NVIDIA/Megatron-LM: Ongoing research training transformer models at scale ，通过GPT的模型运行示例，从三个维…...

编程日记 2023/10/29 10:01:20

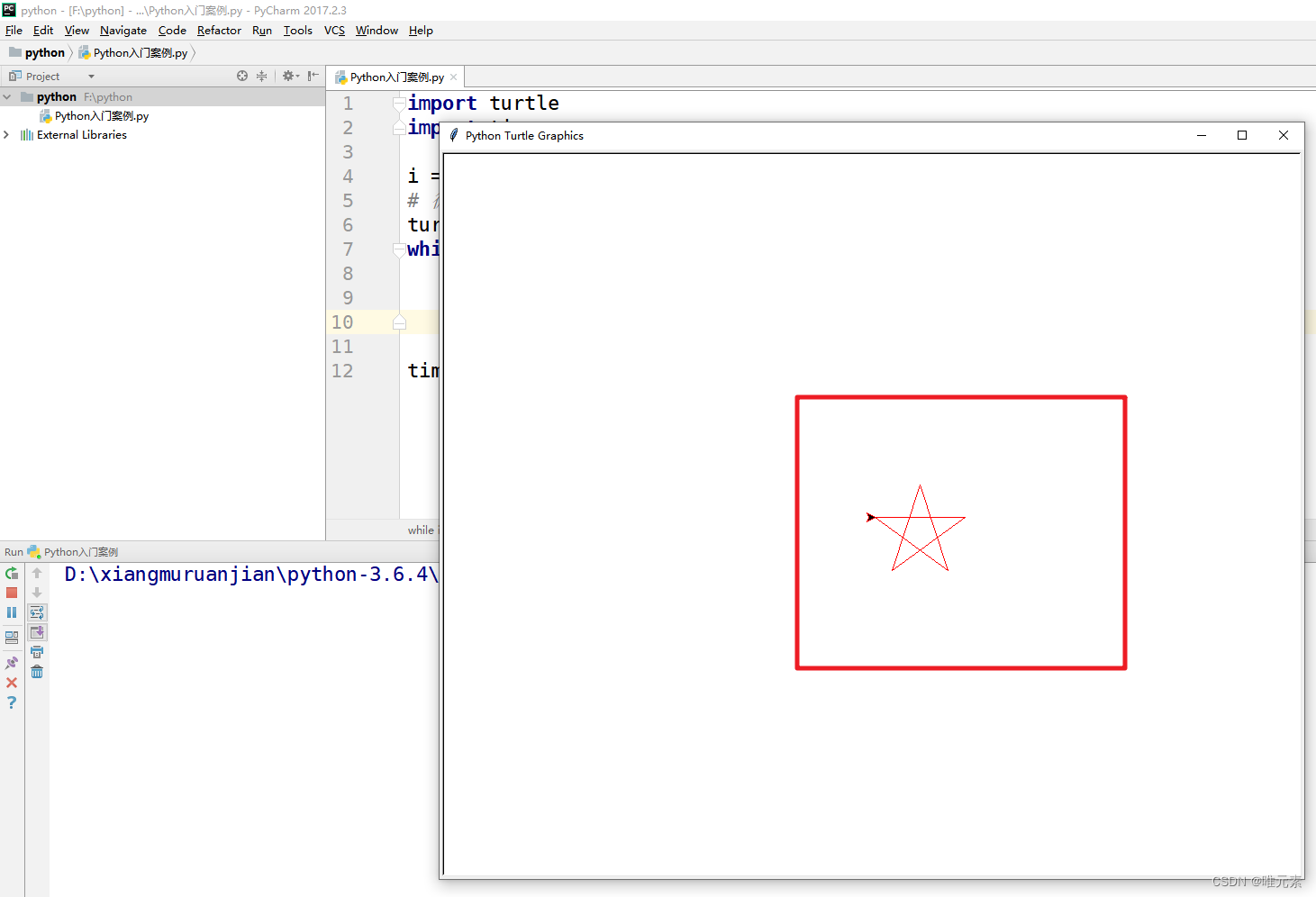
Python---使用turtle模块+for循环绘制五角星---利用turtle（海龟）模块

首先了解涉及的新词汇，编程外国人发明的，所以大部分是和他们语言相关，了解对应意思，可以更好理解掌握。 import 英 /ˈɪmpɔːt/ n. 进口，进口商品；输入，引进；重要性；…...

编程日记 2023/10/29 10:00:19

Python的比较运算符查询表

据个人的编程开发经验，Python的比较运算符最常于条件判断，而条件判断是python编程中最常用的语法之一，与for或while的循环一样，功能十分强大！ 在机器学习当中，或深度学习当中，在运用算法对统计…...

编程日记 2023/10/29 9:59:19

C/C++面试常见问题——const关键字的作用和用法

首先我们需要一下const关键字的定义，const名叫常量限定符，当const修饰变量时，就是在告诉编译器该变量只可访问不可修改，而编译器对于被const修饰的变量有一个优化，编译器不会专门为其开辟空间，而是将变量名…...

编程日记 2023/10/29 9:58:17

Vue3.3指北(四)

Vue3.3指北 1、WebPack - VueCLI1.1、WebPack安装VueCli1.2、vue create 创建项目1.3、项目目录结构介绍 2、ViteVue32.1、认识create-vue2.2、使用create-vue创建项目2.3、项目目录剖析2.4、ESlint代码规范及手动修复2.5、通过eslint插件来实现自动修正 3、VueRouter43.1、单页…...

编程日记 2023/10/29 9:57:17

vue如何使用路由拦截器

在 Vue 中使用路由拦截器需要使用 Vue Router 提供的 beforeEach 方法。beforeEach 方法会在每个路由切换前，对路由进行拦截处理。可以在这个方法中进行一些验证或者权限认证，如果满足条件则继续跳转，否则取消跳转并进行相应处理。 下面是一…...

编程日记 2023/10/29 9:56:16

Docker 深度清除镜像缓存 （overlay2）

Docker 深度清除镜像缓存 （overlay2） 一般情况下，运维清理镜像是通过命令 docker rm i 删除镜像的。但是这条命令不会删除docker build命令产生的缓存文件。 这个时候需要使用 docker system 的系列命令来做相关处理。 docker system --hel…...

编程日记 2023/10/29 9:55:15

刷题笔记（第三天）

1.给定二进制字符串&#xff0c;将其换算成对应的十进制数字 输入&#xff1a;11000000 输出&#xff1a;192 function base10(str) {let sum 0;let a str.split().reverse(); // 个位是第一个元素for (var i 0; i < a.length; i) {suma[i]*Math.pow(2, i);}return sum;…...

编程日记 2023/10/29 9:54:14

Linux常用命令——chown命令

在线Linux命令查询工具 chown 用来变更文件或目录的拥有者或所属群组 补充说明 chown命令改变某个文件或目录的所有者和所属的组&#xff0c;该命令可以向某个用户授权&#xff0c;使该用户变成指定文件的所有者或者改变文件所属的组。用户可以是用户或者是用户D&#xff0…...

编程日记 2023/10/29 9:53:12

浅谈Docker原理

文章目录 前言命名空间控制组分层存储镜像和容器Docker EngineDocker Registry 前言 Docker 是一种容器化技术&#xff0c;它通过利用 Linux 内核提供的虚拟化技术和隔离机制&#xff0c;实现了更轻量级的应用程序虚拟化方案 命名空间 Docker 使用了 Linux 的命名空间特性&a…...

编程日记 2023/10/29 9:52:11

Rt-Thread 移植5--空闲线程和线程阻塞（KF32）

5.1原因 线程延时是浪费CPU资源&#xff0c;受否可以考虑延时的时候放弃CPU使用权&#xff0c;这样就充分利用了CPU的资源。 如果线程进入阻塞状态&#xff0c;没有其他线程运行&#xff0c;是否可以运行一个空闲线程来做一些内存的清理等系统工作呢&#xff1a;5.2 实现 5.2…...

编程日记 2023/10/29 9:51:10

Web3 治理实践探讨：如何寻找多元化发展路径？

Web3 领域变革正崭露头角&#xff0c;而社区治理开始成为行业热议话题。Web3 项目如何探寻多元化建设的解困路径&#xff0c;究竟是治理模型的精进成为首要问题&#xff0c;还是吸纳更多资金与组织教育培训&#xff0c;让开发者成为项目建设的中坚力量&#xff1f;本期 TinTinW…...

编程日记 2023/10/29 9:50:09

探索Vue 3和Vue 2的区别

目录 响应式系统 性能优化 Composition API TypeScript支持 总结 Vue.js是一款流行的JavaScript框架&#xff0c;用于构建用户界面。Vue 3是Vue.js的最新版本&#xff0c;相较于Vue 2引入了许多重大变化和改进。在本文中&#xff0c;我们将探索Vue 3和Vue 2之间的区别。 …...

编程日记 2023/10/29 9:49:07

中微爱芯74逻辑兼容替代TI/ON/NXP工规品质型号全

这里写自定义目录标题 工业级型号全产品线概述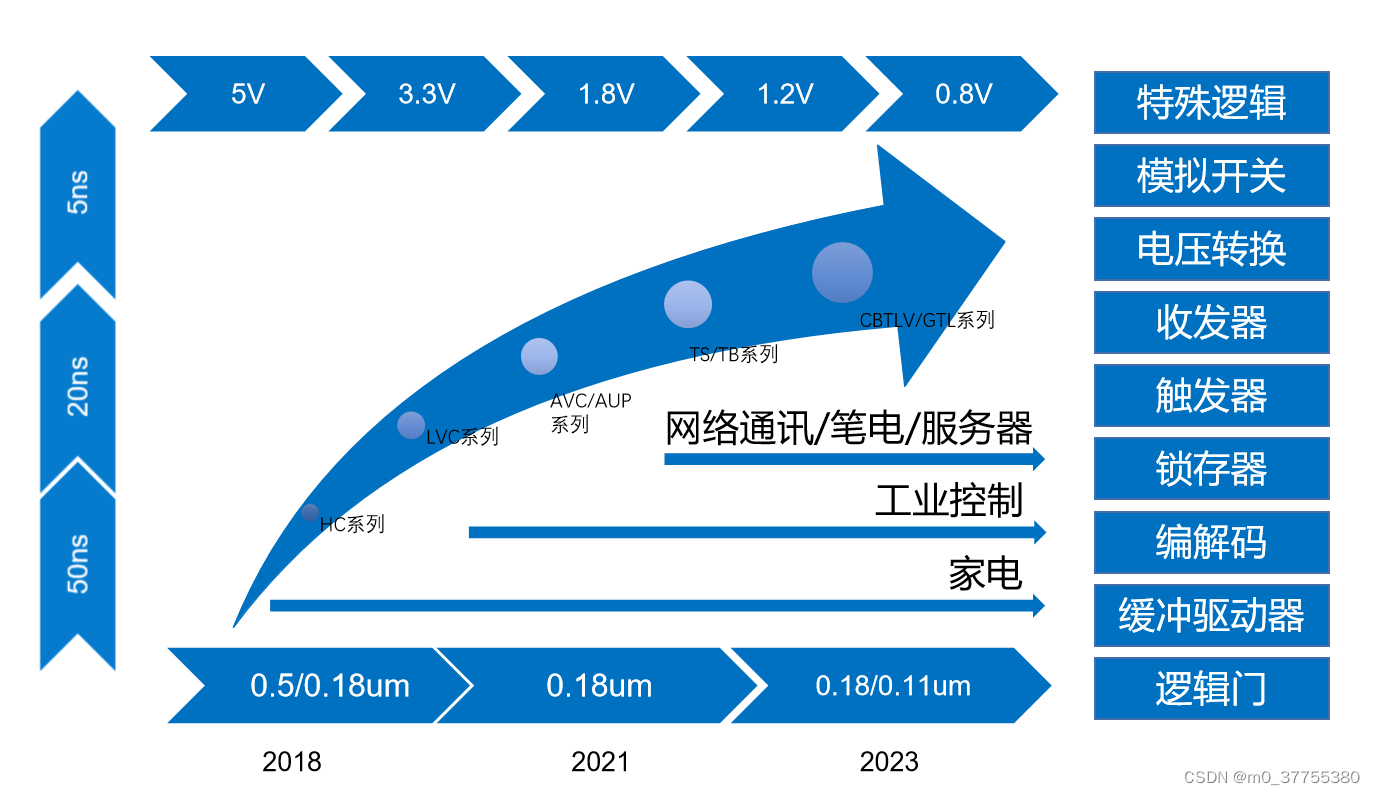![在这里插入图片描述](https://img-blog.csdnimg.cn/097ef810b2234f07b0c0c1e962a73761.png)批量应用行业头部客户兼容替代封装对照逻辑参数对比电平转换系列型号对照HC/HCT 系列型号对照AHC/AHCT 系列型号对照LV/LVC 系列型号对照…...

编程日记 2023/10/29 9:47:04

铭豹扩展坞 USB转网口 突然无法识别解决方法

当 USB 转网口扩展坞在一台笔记本上无法识别，但在其他电脑上正常工作时，问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤，帮助你快速找到故障原因： 背景： 一个M-pard（铭豹）扩展坞的网卡突然无法识别了，扩展出来的三个USB接口正常。…...

编程新知 2026/2/5 10:34:36

微信小程序之bind和catch

这两个呢&#xff0c;都是绑定事件用的&#xff0c;具体使用有些小区别。 官方文档&#xff1a; 事件冒泡处理不同 bind&#xff1a;绑定的事件会向上冒泡&#xff0c;即触发当前组件的事件后&#xff0c;还会继续触发父组件的相同事件。例如&#xff0c;有一个子视图绑定了b…...

编程新知 2026/2/5 5:05:56

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销&#xff0c;平衡网络负载&#xff0c;延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

编程新知 2026/2/6 5:38:46

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例

使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件&#xff0c;常用于在两个集合之间进行数据转移&#xff0c;如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model&#xff1a;绑定右侧列表的值&…...

编程新知 2026/2/4 4:25:40

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括&#xff1a;采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中&#xff0c;设置任务排序规则尤其重要&#xff0c;因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

聊聊 Pulsar：Producer 源码解析

一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台&#xff0c;以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中&#xff0c;Producer&#xff08;生产者&#xff09; 是连接客户端应用与消息队列的第一步。生产者…...

编程新知 2026/2/5 21:34:41

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2026/2/1 5:24:17

3403. 从盒子中找出字典序最大的字符串 I

3403. 从盒子中找出字典序最大的字符串 I 题目链接&#xff1a;3403. 从盒子中找出字典序最大的字符串 I 代码如下&#xff1a; class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

编程新知 2025/10/31 5:18:02

深度学习习题2

1.如果增加神经网络的宽度&#xff0c;精确度会增加到一个特定阈值后&#xff0c;便开始降低。造成这一现象的可能原因是什么&#xff1f; A、即使增加卷积核的数量&#xff0c;只有少部分的核会被用作预测 B、当卷积核数量增加时&#xff0c;神经网络的预测能力会降低 C、当卷…...

编程新知 2026/1/26 5:53:30

《C++ 模板》

目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板&#xff0c;就像一个模具&#xff0c;里面可以将不同类型的材料做成一个形状&#xff0c;其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式&#xff1a;templa…...

编程新知 2025/6/11 3:20:47