C语言浮点型在内存中的存储
目录
前言:
引言:
浮点数存储规则
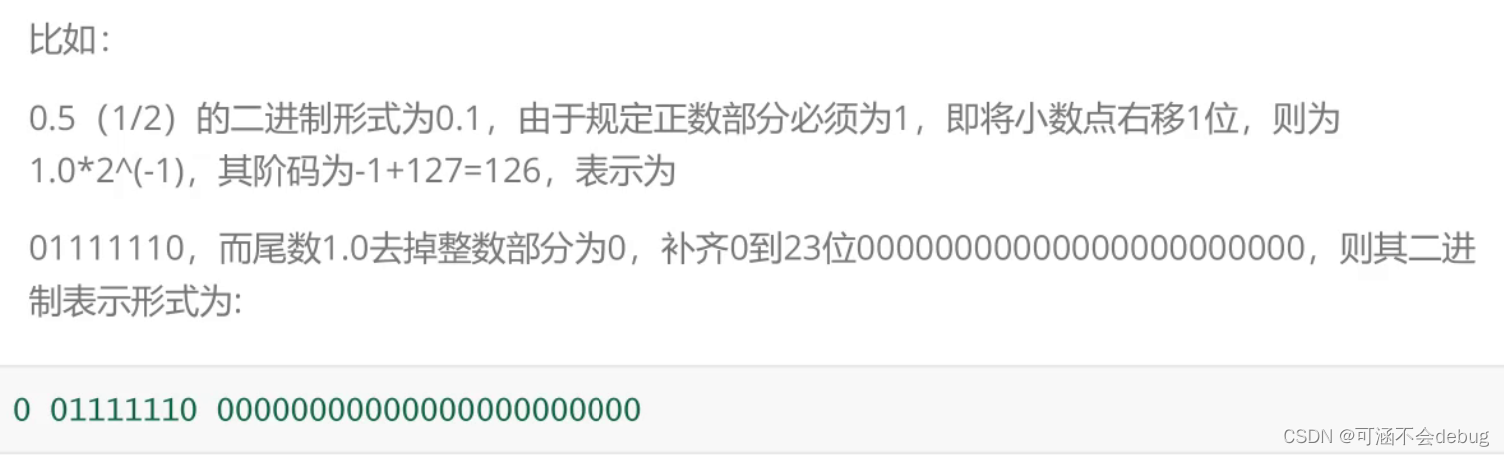
举个栗子:
TIP:
单精度浮点数存储的模型(float)
双精度浮点数存储的模型(double)
IEEE对 M 的特殊规定
IEEE对 E 的特殊规定
小试牛刀
先看第一段代码
再看第二段代码
前言:
我们首先需要知道什么是浮点型,以下是两种常见的浮点型。
3.14159 ------------- 这是最常见的浮点型,也就是小数。
1E10 ------------- 这个也表示浮点型,E表示底数10,而E后面的数表示指数,所以E10就是10^10,而E前面的1是数量级,综上,1E10就是1*10^10。
引言:
我们先看一段代码
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}输出结果:

我们不难发现,当n以整型的方式存进去,然后分别以整型和浮点型的方式取出,发现以浮点型的方式打印结果有问题;对应的,当n以浮点型的方式存进去,再以整型的方式取出,结果也是跟我们想象的不一样。
由此,可以得出一个结论,浮点型在内存中的存储和整型在内存中的存储是不一样的。
浮点数存储规则
根据国际标准IEEE,任意一个二进制浮点数V可以表示成下面的形式:
- (-1)^ S * M * 2 ^ E
- (-1) ^ S表示符号位,当S=0,V是正数,当S=1,V是负数。
- M表示有效数字,大于等于1,小于2
- 2^E表示指数位。
举个栗子:
十进制表示的5.5
首先5的二进制位就是101,而小数部分0.5我们就用1来表示,最终结果就是101.1
为何小数部分用1表示就可以呢?
因为整数部分个位数的权重是2^0,十位数的权重是2^1,百位数的权重是2^2,以此类推,小数部分的第一位表示2^(-1),也就是0.5,小数部分的第二位就是2^(-2)……
因此我们用IEEE表示就是
(-1)^ 0 * 1.011 * 2 ^ 2
所以S=0,M=1.011,E=2
TIP:
理论上任何一个浮点型都可以用IEEE表达形式表示,但如果浮点数过于复杂,就不能精准的表示出来。
比如3.14,小数部分想要表示出0.14,需要我们一直凑,但大概率是凑不出来,会有一些误差!
单精度浮点数存储的模型(float)
对于32位的浮点数,最高的1位是符号位S,接着的8位是指数E,剩下的23位比特位是有效数字M
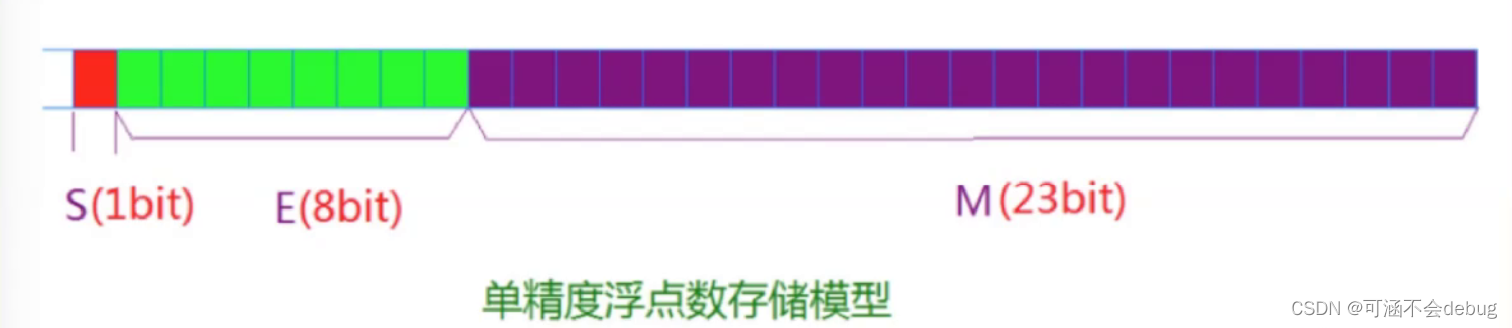
双精度浮点数存储的模型(double)
对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M

IEEE对 M 的特殊规定
前面说过,1<=M<2,所以,M可以写成1.xxxxxxxx的形式,其中xxxxxxxxx表示小数部分。
IEEE规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxxx小数部分。
比如保存1.01时,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的是,节省1位有效数字,是的表达小数部分更精确。
IEEE对 E 的特殊规定
首先,E作为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围是0~255,如果是11位,他的取值范围是0~2047。
但是,我们知道,科学技术法中是可以出现负数的。
所以IEEE规定,存入内存时E的真实值必须加上一个中间数,对于8位的E来说,这个中间数的值就是127,对于11位的E来说,这个中间值就是1023。
我们取出来时,还是需要减去中间数的。
上面讲的内容是讲E如何存储到内存中的,下面开始讲解如何把E取出来。
- E不为全0或不全为1
这是最普遍的情况,我们将指数E的值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1
- E全为0
表示原有的真实值是-127,2^-127是一个非常小的数字,无限接近于0,所以有效数字M不再加上第一位的1,而是还原0.xxxxxxxx的小数,使得接近于0。
- E全为1
表示是2^128次方,是一个非常大的数字,所以表示正负无穷大(正负取决于符号位S)。
小试牛刀
我们现在已经大致掌握了浮点型在内存如何存储和取出,让我们来解决一下引言的问题吧!
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);
//分为两段,我们一段一段去解决*pFloat = 9.0;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}先看第一段代码
9在整型n中的存储形式是
00000000000000000000000000001001
然后我们照搬,将其存储在浮点型
0 00000000 00000000000000000001001
S E M
可以看出E是全0,根据IEEE规定,当E为全0时,我们对于M不需要补数字1,而现在的M也是一个非常小的数字,当我们用%f打印时,只能保留6位有效数字,因此打印结果就是0.000000
再看第二段代码
我们首先是将9.0存储再一个浮点型中
9.0在浮点型中存储的二进制位表达形式是
1001.0
1.001*2^3 (注意一定要表示成科学技术法的形式!再找S、M、E)
S=0 M=1.001(存储在内存就是001) E=3(3+127)
0 10000010 0010000000000000000000
注意M = 001存储直接放在最前面
而将这一部分照搬到整型,发现结果就是一个非常大的数字!1091567616
相关文章:

C语言浮点型在内存中的存储
目录 前言: 引言: 浮点数存储规则 举个栗子: TIP: 单精度浮点数存储的模型(float) 双精度浮点数存储的模型(double) IEEE对 M 的特殊规定 IEEE对 E 的特殊规定 小试牛刀 先…...

elementPlus | el-tabs 标签管理路由页面
<script setup> import { useRouter } from vue-router const router useRouter()const tabClick (tab)>{const idx tab.indexif(idx 0){router.push(/)}... } </script> <template><!-- 撑开 stretch"true" --><el-tabs type&quo…...

如何使用ffmpeg制作透明背景的视频
最近我们尝试在网页上叠加数字人讲解的功能,发现如果直接在网页上放一个矩形的数字人视频,效果会很差,首先是会遮挡很多画面的内容,其次就是不管使用任何任务背景,画面都和后面的网页不是很协调,如图所示&a…...

C#中对于using的使用方式
导入命名空间 使用list需要导入 System.Collections.Generic;这个命名空间 using System.Collections.Generic; using UnityEngine;public class UsingTest : MonoBehaviour {void Start(){List<int> intlist new List<int>();} }省略类名 using UnityEngine; …...
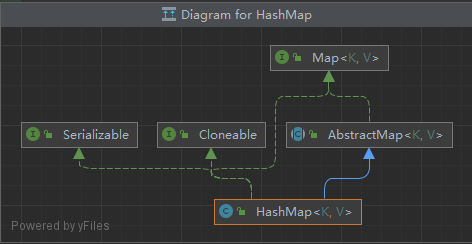
【Java】HashMap集合
Map集合概述和使用 Map集合概述 Interface Map<k,v> k:键值类型 v:值的类型 Map集合的特点 键值对 映射关系 Key 和 Value一个键(Key)对应一个值(Value)键不允许重复,值可以重复如…...

百度网盘使用指南
文章目录 备份篇手机文件备份电脑文件备份 查找篇移动端PC端 文件操作文件解压文件扫描PDF工具图片工具音频操作 备份篇 手机文件备份 在百度网盘APP种点击 我的–设置–自动备份设置 里边有相册备份, 文档备份, 微信文件备份, 手机通讯录, 短信, 通话备份等功能 电脑文件备…...
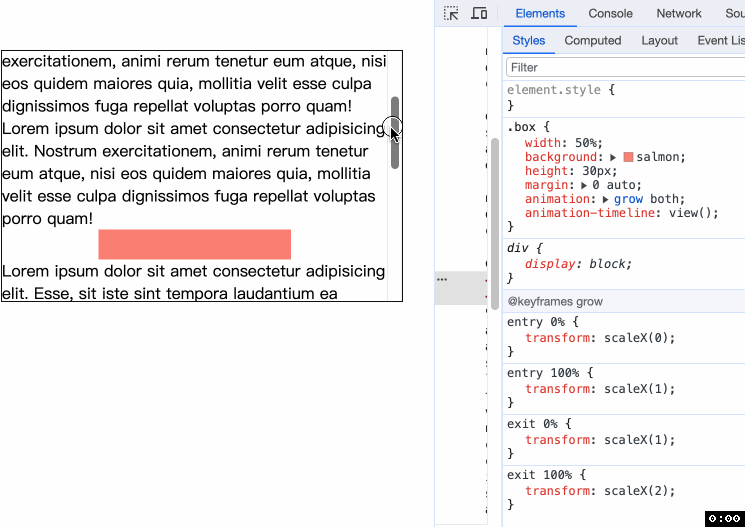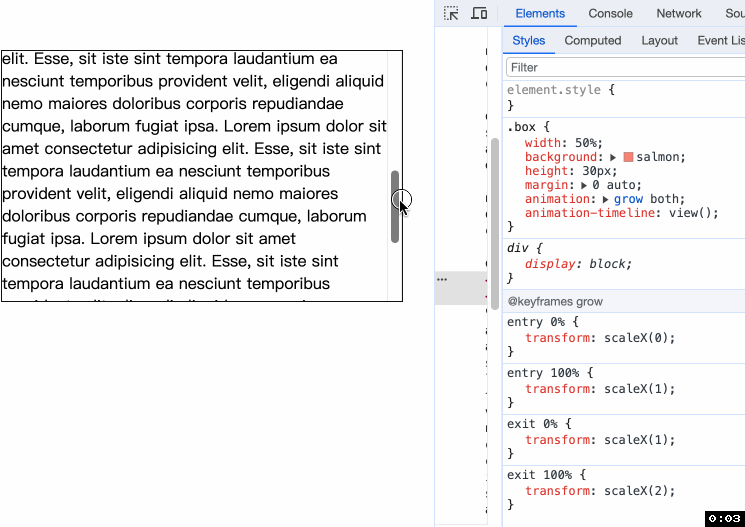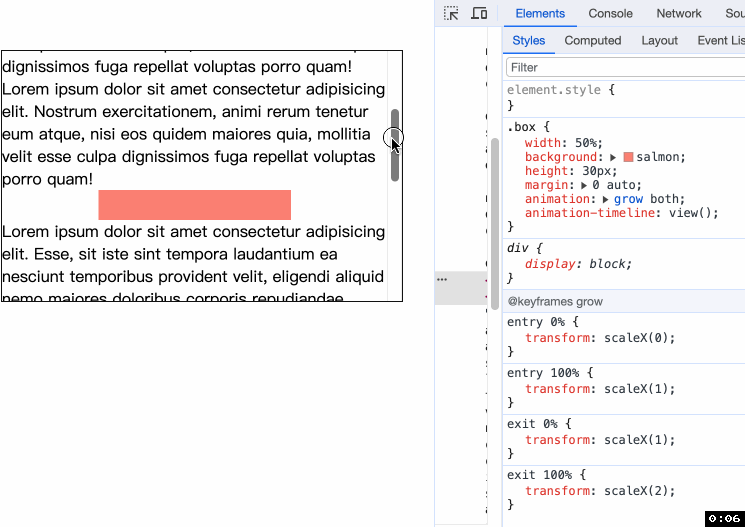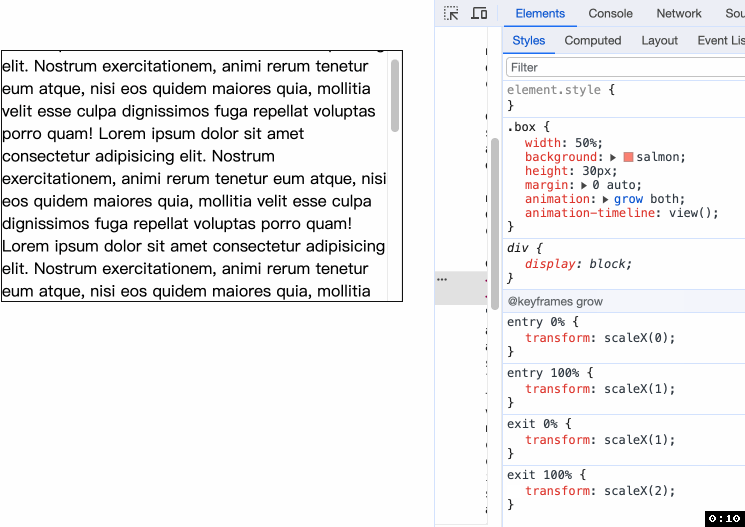
CSS 滚动驱动动画与 @keyframes 新语法
CSS 滚动驱动动画与 keyframes 在 CSS 滚动驱动动画相关的属性出来之后, keyframes 也迎来变化. 以前, keyframes 的值可以是 from, to, 或者百分数. 现在它多了一种属性的值 <timeline-range-name> <percentage> 建议先了解 animation-range 不然你会对 timeli…...

二十三种设计模式全面解析-原型模式进阶之原型管理器:集中管理对象原型的设计模式之道
在软件开发中,我们经常需要创建和复制对象。然而,有时候直接创建对象可能会导致性能下降或代码重复。为了解决这些问题,原型模式应运而生。而使用原型管理器(Prototype Manager)来集中管理原型对象可以进一步提高灵活性…...

【微信小程序开发】学习小程序的网络请求和数据处理
前言 网络请求是微信小程序中获取数据和与服务器交互的重要方式。微信小程序提供了自己的API来处理网络请求,使得开发者可以轻松地在微信小程序中实现数据的获取和提交。本文将介绍微信小程序中的网络请求,包括使用wx.request发起GET和POST请求…...
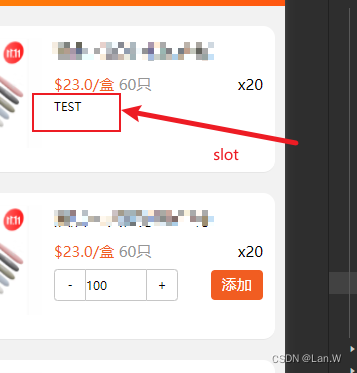
微信小程序 slot 不显示
问题:创建组件,使用带名字的slot,页面调用组件使用slot不显示 源码: 组件xml <view class"p-item br24" style"{{style}}"><slot name"right" wx:if"{{!custBottom}}"></slot>&l…...

Spring Boot 优雅配置yml配置文件定义集合、数组和Map
一、value 获取配置文件 在平时的yml配置文件中,我们经常使用到配置基本数据类型的字符串,比如配置日志文件的写法如下: # 配置日志输出级别 logging:# 指定logback配置文件的位置 config: classpath:logback-spring.xml# 文件日志要输出的路…...
java+springboot+vue开发的大学生健康检测小程序
主要功能测试身体健康指数,添加病历,添加日历清单等,管理员导出学生健康电子档案表等。前端小城程序,后端管理员vue开发,接口Java springboot开发。 小程序演示视频 https://www.bilibili.com/video/BV1Kc411d7bb/?s…...
从零开始的LINUX(四)
1.yum: 功能:软件包管理器,功能类似与手机上的应用商店。通过yum可以获取指令的下载地址,然后一键式安装指令。由于yum中的地址一般都是外网的,所以需要镜像源(即国内的下载地址)。 相关指令&…...

组播应用层收不到问题-接收网卡绑定
问题背景: 平台:Android 设备A:组播发送者,发送组播数据 设备B:组播接受者,接收组播数据 设备A与设备B通过有线连接,连接在设备B的eth0网卡上 问题: 设备B在没有通讯模块网卡的情况…...

回流重绘零负担,网页加载快如闪电
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、回…...
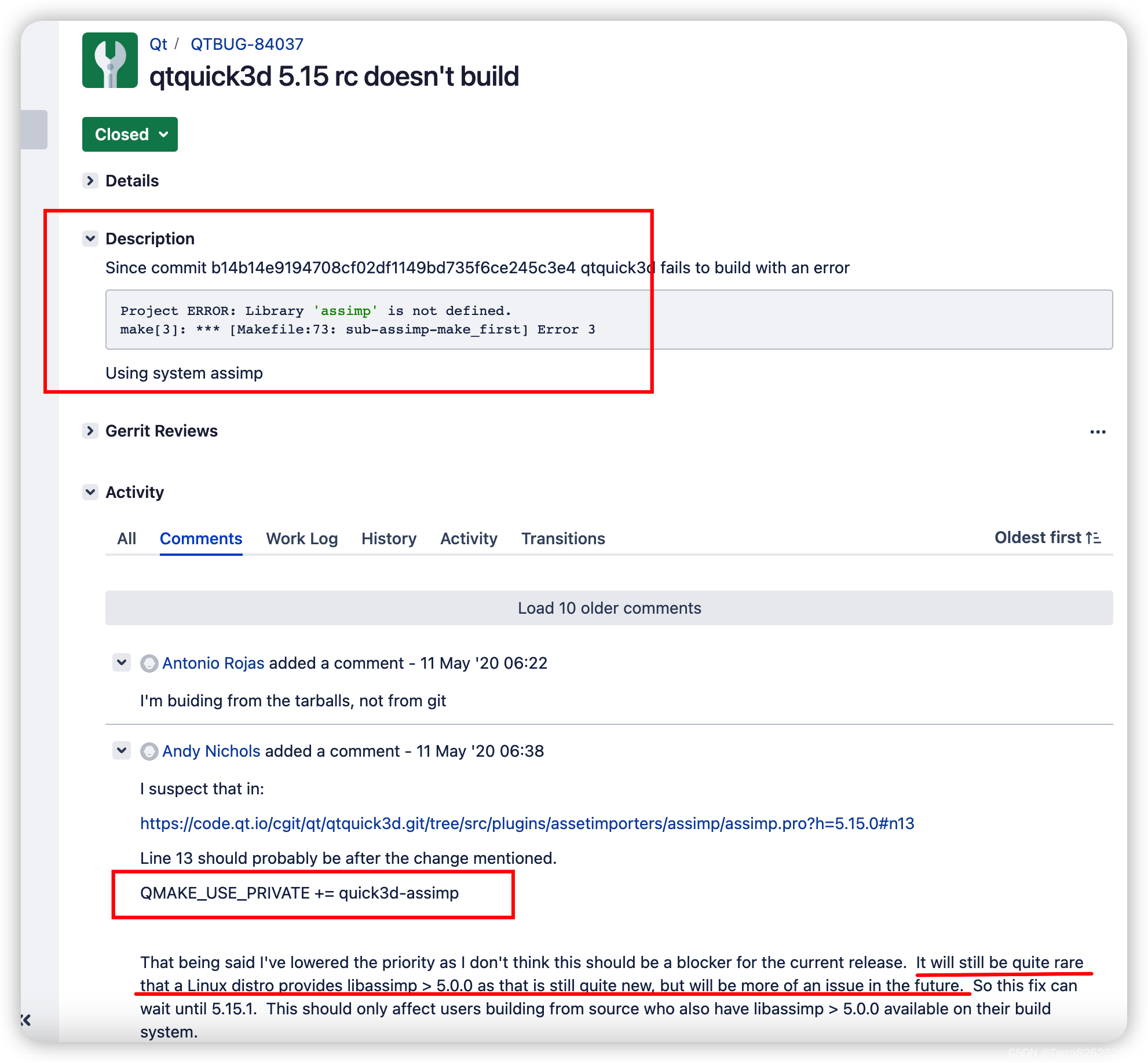
QT5.15在Ubuntu22.04上编译流程
在我们日常遇到的很多第三方软件中,有部分软件针对开发人员,并不提供预编译成果物,而是需要开发人员自行编译,此类问题有时候不是问题(编译步骤的doc详细且清晰时),但有时候又很棘手(…...
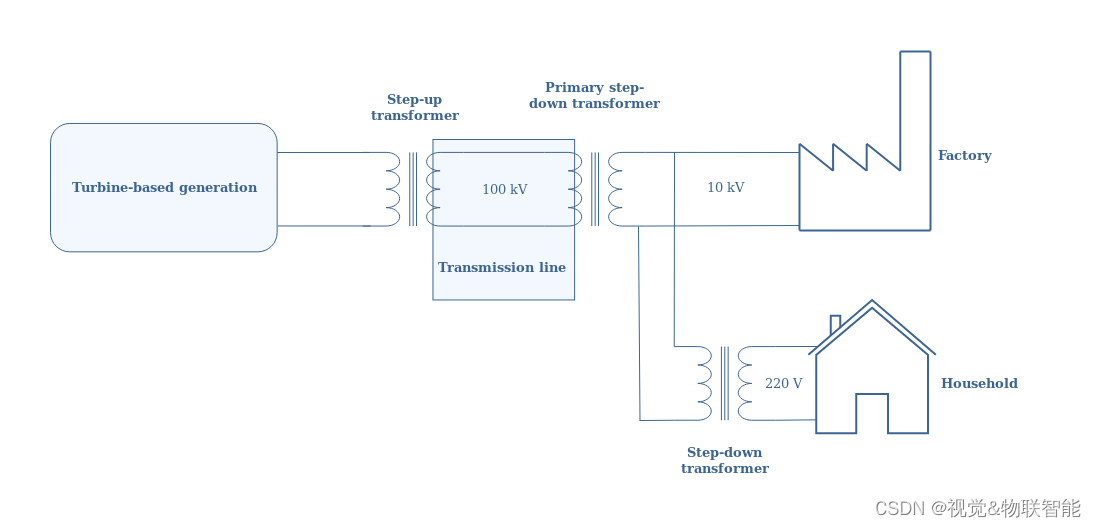
【电路笔记】-交流波形和交流电路理论
交流波形和交流电路理论 文章目录 交流波形和交流电路理论1、概述2、交流发电2.1 涡轮发电2.2 变压器 3、交流功率3.1 RMS值3.2 功率分配 4、总结 当谈论电流或电压时,这些信号可以分为两大类:直流和交流。 DC 状态为“直流电”,该定义重新组…...

vue2 系列:自定义 v-model
1. input 中的 v-model <!-- 表单双向绑定 --> <input :value"username" input"username $event.target.value" /> <!-- 等于 --> <input v-model"username" /> 2. 自定义组件 v-model <!-- 组件双向绑定 -->…...

广东木模板批发,建筑桥梁工程专用组合木模板
作为广东地区的木模板批发商,我们致力于为建筑行业提供高品质的木模板产品。在众多产品中,我们特别推荐我们的建筑桥梁工程专用组合木模板,为桥梁工程提供卓越的支持和出色的性能。 我们的组合木模板是专为桥梁工程设计的,以满足对…...
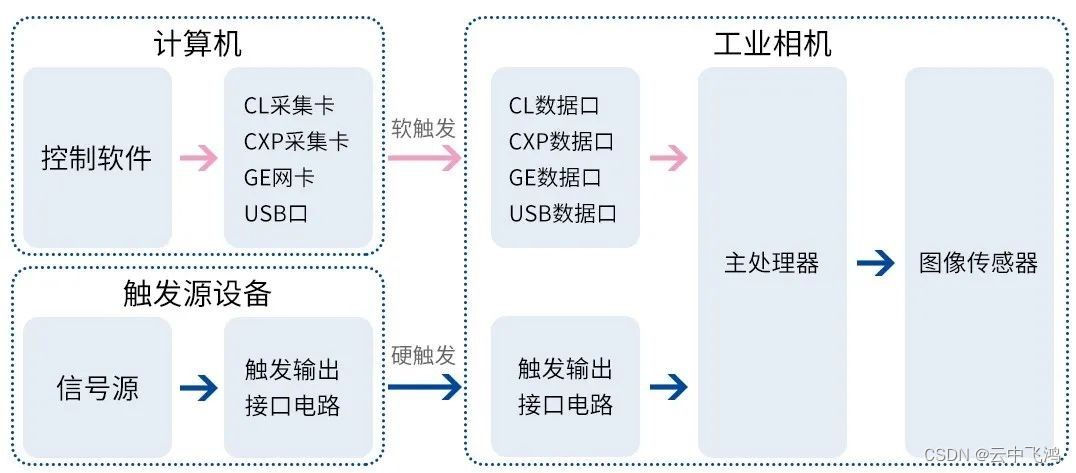
工业相机常见的工作模式、触发方式
参考:机器视觉——工业相机的触发应用(1) - 知乎 工业相机常见的工作模式一般分为: 触发模式连续模式同步模式授时同步模式 触发模式:相机收到外部的触发命令后,开始按照约定时长进行曝光,曝光结束后输出一帧图像。…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
