深入浅出排序算法之堆排序
目录
1. 算法介绍
2. 执行流程⭐⭐⭐⭐⭐✔
3. 代码实现
4. 性能分析
1. 算法介绍
堆是一种数据结构,可以把堆看成一棵完全二叉树,这棵完全二叉树满足:任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值。若父亲大孩子小,则这样的堆叫作大顶堆;若父亲小孩子大,则这样的堆叫作小顶堆。
根据堆的定义知道,代表堆的这棵完全二叉树的根结点的值是最大(或最小)的,因此将一个无序序列调整为一个堆,就可以找出这个序列的最大(或最小)值,然后将找出的这个值交换到序列的最后(或最前),这样,有序序列关键字增加1个,无序序列中关键字减少1个,对新的无序序列重复这样的操作,就实现了排序。这就是堆排序的思想。
堆排序中最关键的操作是将序列调整为堆。整个排序的过程就是通过不断调整,使得不符合堆定义的完全二叉树变为符合堆定义的完全二叉树。
2. 执行流程⭐⭐⭐⭐⭐✔
建堆是先从自下而上,从右往左建
初始堆的每一个结点都要满足堆的定义,也就是父节点的值大于左右孩子结点的值!!!
选出最大值,是将根结点和最后一个结点互换,然后继续构建大顶堆!!!
⭐⭐⭐堆顶和最后一个元素交换,才算一趟,也是该趟的最终序列结果!!!
建堆和排序结果是两个阶段,但同属于一趟中。
图示如下:


3. 代码实现
为了三个步骤:
步骤一:先建堆(大根堆或者小根堆)
步骤二:交完堆顶和最后一个元素,然后堆的大小减一
步骤三:向下调整堆
步骤一只需实现一次,步骤二和步骤三循环执行,得到最终的有序序列。
//开始排序:堆排序分为三个功能 ①开始建堆,②交换,③向下调整,重复②和③步public static void heapSort(int[] array,int len){int end = len - 1;//确定最后一个结点的下标createHeap(array);//建堆//当只剩下一个结点的时候,就不需要交换while(end > 0){//交换swap(array,0,end);//向下调整shiftDown(array,0,end);//调整完一个结点,下一个end--;}}//交换数据public static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}//堆排序(大根堆)//从上往下建堆,所以先找父节点,再找孩子结点public static void createHeap(int[] array){for(int parent = (array.length - 1 - 1) / 2;parent >= 0;parent--){shiftDown(array,parent,array.length);}}//向下调整public static void shiftDown(int[] array,int parent,int len){//定义一个记录孩子下标的变量(左孩子)int child = 2 * parent + 1;//判断父节点和孩子结点的大小,至少左孩子要存在while(child < len){//比较左右孩子if((child + 1) < len && array[child] < array[child + 1]){child++;}//判断父节点和孩子节点if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = 2 * parent + 1;}else{break;}}}
public static void main(String[] args) {int[] a = {5,4,3,2,1};Sort.heapSort(a, a.length);for (int x : a) {System.out.print(x + " ");}}
4. 性能分析
| 时间辅助度 | 空间复杂度 |
| O(N*logN) | O(1) |
| 数据不敏感 | 数据不敏感 |
稳定性:不稳定。
来上解析,怎么计算这个时间复杂度。
(1)步骤一的时间复杂度:首先知道有N个结点开始建堆,这个时间复杂度就是O(N),大家可以去看看这篇文章,里面有讲建堆的时间复杂度。链接如下:
数据结构——堆、堆排序和优先级队列(代码为Java版本)
(2)步骤二和步骤三循环的时间复杂度:那么我第一个结点交换时,需要向下调整为log(N - 1)层;交换第二个结点后,需要向下log(N - 2),接下来就是log(N - 3),log(N - 4),……,log1。所以总的调整次数是log(N - 1) + log(N - 2) + log(N - 3) + log(N - 4) + …… + log1 = log((N - 1)!)。
我们可以在网上看到堆排序的时间复杂度是O(N*logN),这是堆排序的大致估算(我们算时间复杂度都是算个大概),其实log((N - 1)!) 约等于 NlogN。下面是我的证明结果:
① 使用夹逼准则证明:
先求上限:
再求下限:
因为
所以
当 时,
② 则有:
③结论: 既是
的低阶函数,又是
的高阶函数,因此是
的同阶函数!
(3)由于上面的证明步骤,我们可以知道堆排序的时间复杂度是 。
相关文章:
深入浅出排序算法之堆排序
目录 1. 算法介绍 2. 执行流程⭐⭐⭐⭐⭐✔ 3. 代码实现 4. 性能分析 1. 算法介绍 堆是一种数据结构,可以把堆看成一棵完全二叉树,这棵完全二叉树满足:任何一个非叶结点的值都不大于(或不小于)其左右孩子结点的值。若父亲大孩子小&#x…...
—— tcpdump)
Linux 命令(11)—— tcpdump
文章目录 一、命令简介二、使用方法三、命令选项四、基本语法和使用方法1. 显示 ASCII 字符串2. 抓取特定协议的数据3. 抓取特定主机的数据4. 将抓取的数据写入文件5. 行缓冲模式 五、理解tcpdump的输出六、过滤表达式1. Host 过滤2. Network 过滤3. Proto 过滤4. Port 过滤5. …...
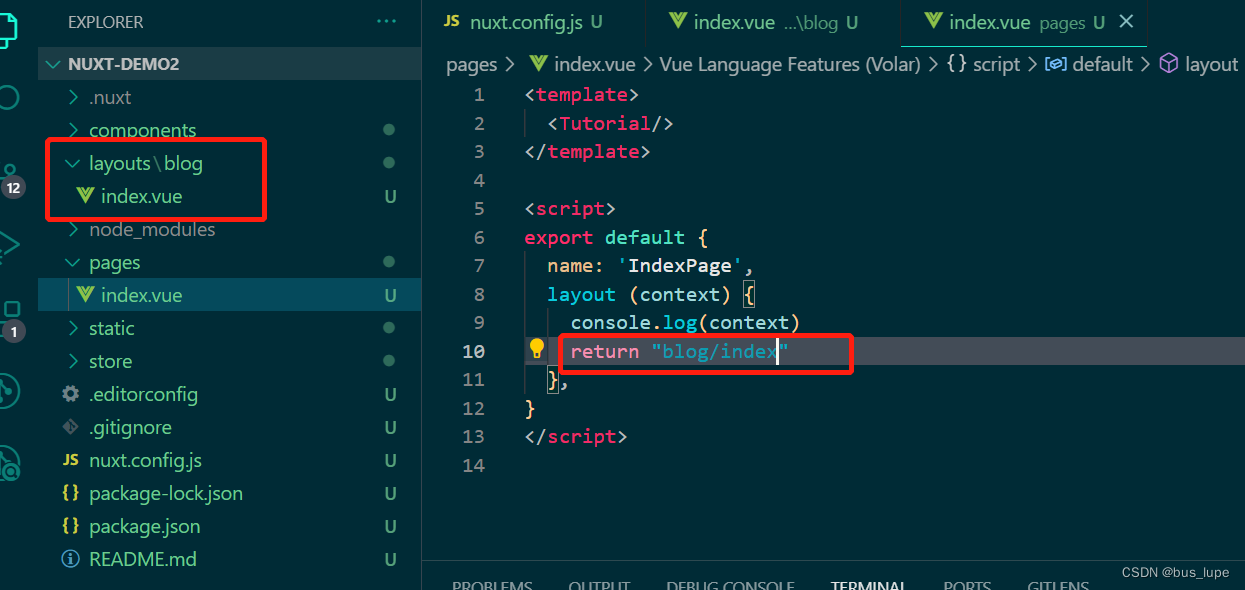
8.自定义组件布局和详解Context上下文
pages/index.vue layout布局运行在服务端 1、在项目的目录下新建layout文件夹,并新建一个blog.vue布局文件 2、在页面中的layout函数里,返回刚才新建布局文件的名字blog就可以使用了 export default {...layout (context) {console.log(context)retu…...
几个Web自动化测试框架的比较:Cypress、Selenium和Playwright
介绍:Web自动化测试框架对于确保Web应用程序的质量和可靠性至关重要。它们帮助开发人员和测试人员自动执行重复性任务,跨多个浏览器和平台执行测试,并在开发早期发现问题。 以下仅代表作者观点: 本文探讨来3种流行的Web自动化测…...
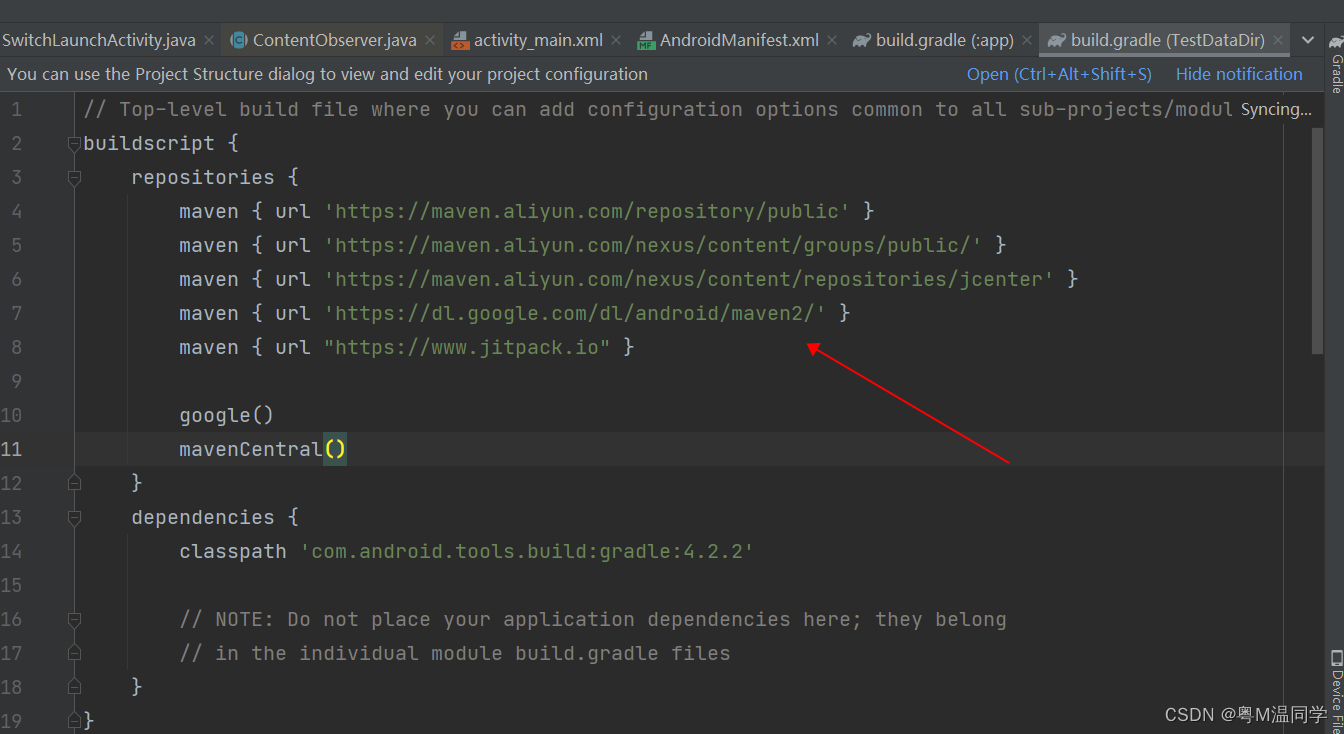
Android Studio中配置aliyun maven库
当下载第三方库失败的时候,通过Android Studio中配置aliyun maven库,达到正常下载库效果 在项目的根build.gradle里面(不是module)buildscriptde对应位置添加配置: maven { url https://maven.aliyun.com/repository/…...

记录使用阿里 ARoute 遇到的坑
1.按照官方一个配置好之后 尝试使用 跳转出现 Aroute Theres no route matched path"" 我这边遇到的坑是配置问题 kotiln 使用了 Java的配置 plugins {id("com.android.application")id("org.jetbrains.kotlin.android")id("kotlin-kapt&…...

lesson2(补充)关于const成员函数
个人主页:Lei宝啊 愿所有美好如期而遇 前言: 将const 修饰的 “ 成员函数 ” 称之为 const 成员函数 , const 修饰类成员函数,实际修饰该成员函数 隐含的 this 指针 ,表明在该成员函数中不能对类的任何成员进行修改…...
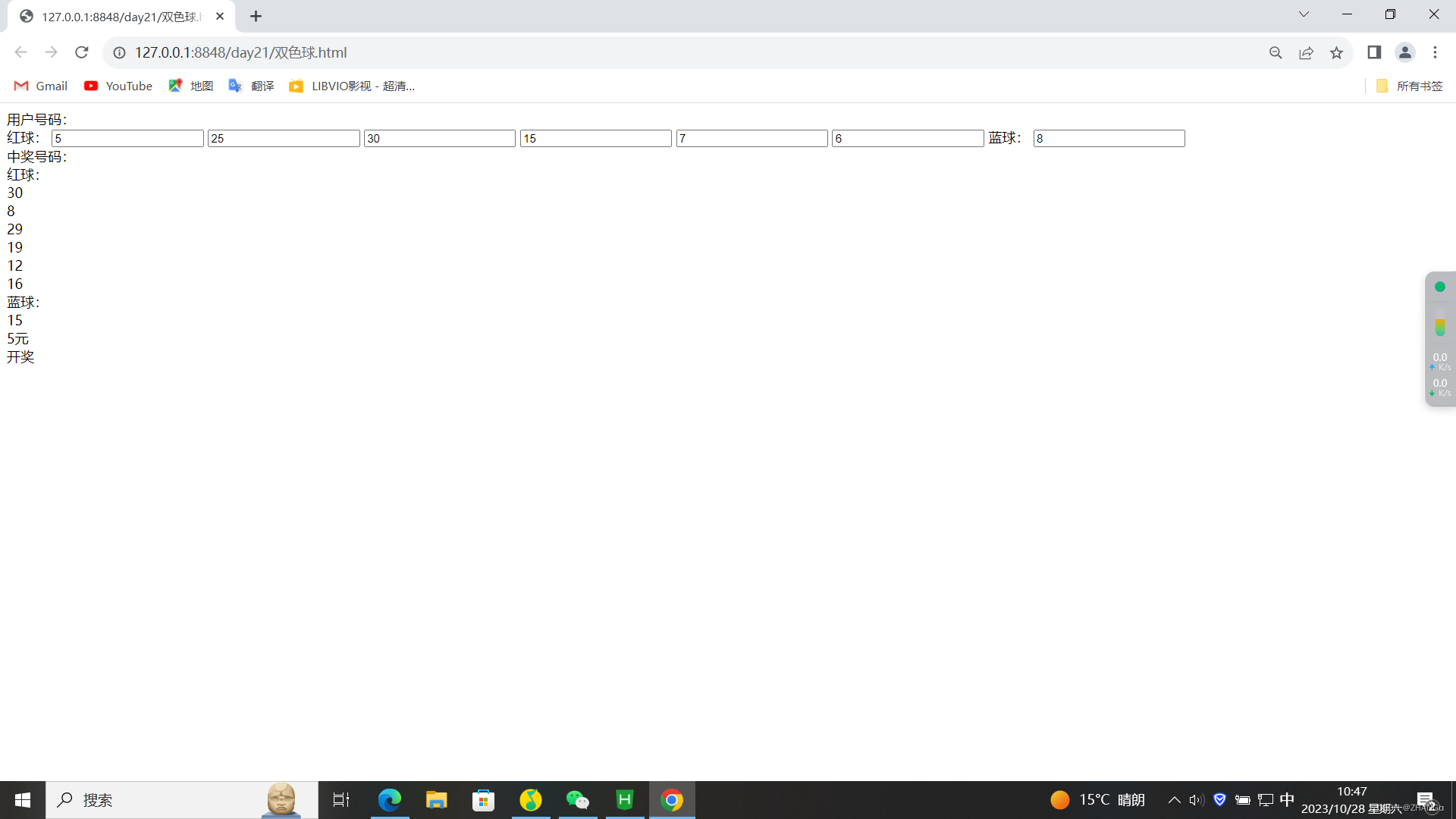
前端 :用HTML ,JS写一个 双色球彩票中将机制,因为时间不够,加上本人懒没有用CSS美化界面,多包涵
1.HTML <body><div id"content"><div id "top"><div id "username">用户号码:</div><div id "qiu"><span id "red">红球:</span><input id…...

前端页面如何自适应--4种方法
前端页面有很多方法可以实现。这里我将介绍五种常用的方法,并提供相应的代码示例。 1. 使用CSS媒体查询 通过CSS媒体查询,可以根据不同的屏幕尺寸应用不同的样式。在Vue组件中,可以在样式部分使用媒体查询,使排版根据屏幕大小进…...
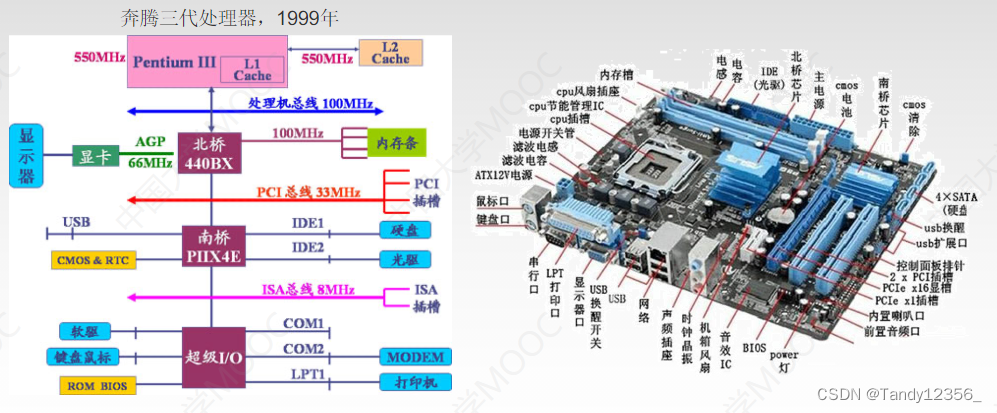
2024王道考研计算机组成原理——总线
6.1 总线概述 每一个外设都通过IO接口和DB、CB、AB相连 三系统总线结构: 桥有总线仲裁的功能,就是把某一总线的使用权分给哪个设备? 6.1.2 总线的性能指标 总线复用:分时传输地址&数据 6.2 总线仲裁 通过控制总线来发送使…...

【Linux】进程概念(下)
进程概念 一、环境变量1. 命令行参数2. 常见的环境变量(1)PATH(2)PWD(3)HOME(4)env 查看所有的环境变量 3. 获取环境变量(1)通过代码获取环境变量(…...
基于Spring Boot的本科生就业质量设计与实现
摘 要 信息化爆炸的时代,互联网技术的指数型的增长,信息化程度的不断普及,社会节奏在加快,每天都有大量的信息扑面而来,人们正处于数字信息化世界。数字化的互联网具有便捷性,传递快,效率高&am…...

238. 除自身以外数组的乘积 --力扣 --JAVA
题目 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请不要使用除法,且在 O(n) 时间复…...

如何判断一个类是线程安全的
线程安全 一个类或者程序提供的接口,多个线程之间的切换不会导致该接口的执行结果存在二义性,也就是不必考虑同步问题。 或者说一段代码可能会被多个线程同时执行,如果每次运行的结果和单线程执行的结果是一样的,并且其他变量的…...

MyBatis的各种查询功能
文章目录 情景查询一个实体类对象查询一个List集合查询单个数据查询一条数据为map集合查询多条数据为map集合方法一方法二 情景 如果查询出的数据只有一条,可以通过 实体类对象接收List集合接收Map集合接收,结果{password123456, sex男, id1, age23, us…...

【Tomcat】如何在idea上部署一个maven项目?
目录 1.创建项目 2.引入依赖 3.创建目录 4.编写代码 5.打包程序 6.部署项目 7.验证程序 什么是Tomcat和Servlet? 以idea2019为例: 1.创建项目 1.1 首先创建maven项目 1.2 项目名称 2.引入依赖 2.1 网址输入mvnrepository.com进入maven中央仓库->地址…...

Three.js 材质的 blending
Three.js 材质的 blending // blending modes export type Blending | typeof NoBlending| typeof NormalBlending| typeof AdditiveBlending| typeof SubtractiveBlending| typeof MultiplyBlending| typeof CustomBlending;// custom blending destination factors export t…...

关于pcl 给new出的数据赋值报错问题
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>); for (size_t i 0; i < cloud->points.size (); i) //填充数据 { cloud->points[i].x 1024 * rand () / (RAND_MAX 1.0f); cloud->points[i].y 1024…...
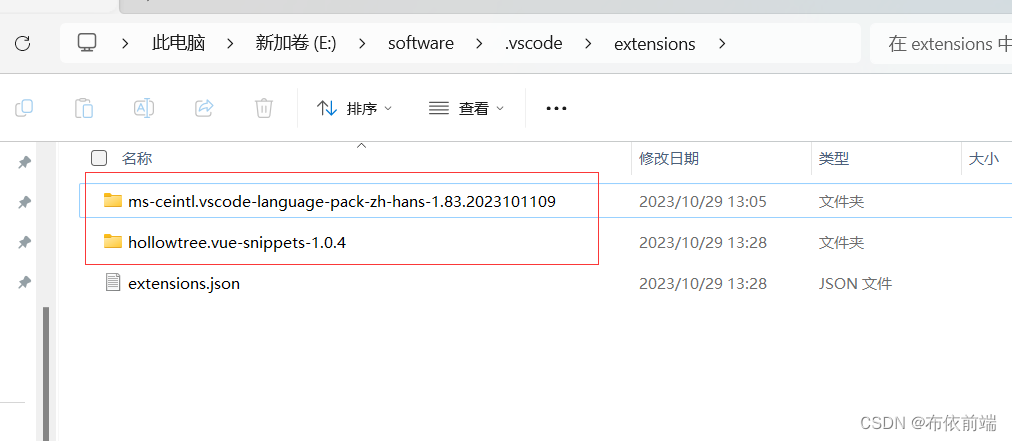
window11 更改 vscode 插件目录,释放C盘内存
由于经常使用vscode开发会安装一些代码提示插件,然后C盘内容会逐渐缩小,最终排查定位到vscode。这个吃内存不眨眼的家伙。 建议:不要把插件目录和vscode安装目录放在同一个位置,不然这样vscode更新后,插件也会消失。 v…...
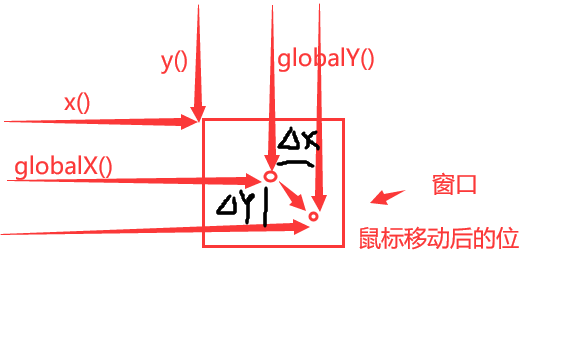
【PyQt学习篇 · ⑥】:QWidget - 事件
文章目录 事件消息显示和关闭事件移动事件调整大小事件鼠标事件进入和离开事件鼠标按下和释放事件鼠标双击事件鼠标按下移动事件 键盘事件焦点事件拖拽事件绘制事件改变事件右键菜单输入法 事件转发机制案例一案例二案例三 事件消息 显示和关闭事件 showEvent(QShowEvent)方法…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
