笔记本电脑搜索不到wifi6 无线路由器信号
路由器更换成wifi6 无线路由器后,手机能搜索到这个无线信号,但是笔记本搜索不到这个无线信号,后网上搜索后发现是无线网卡驱动问题,很多无线网卡使用的是Intel芯片,Intel就此发布了公告,升级驱动就可以彻底解决。
下载Intel无线网卡驱动链接地址
下载 英特尔® PROSet/无线软件 和 Wi-Fi 驱动程序

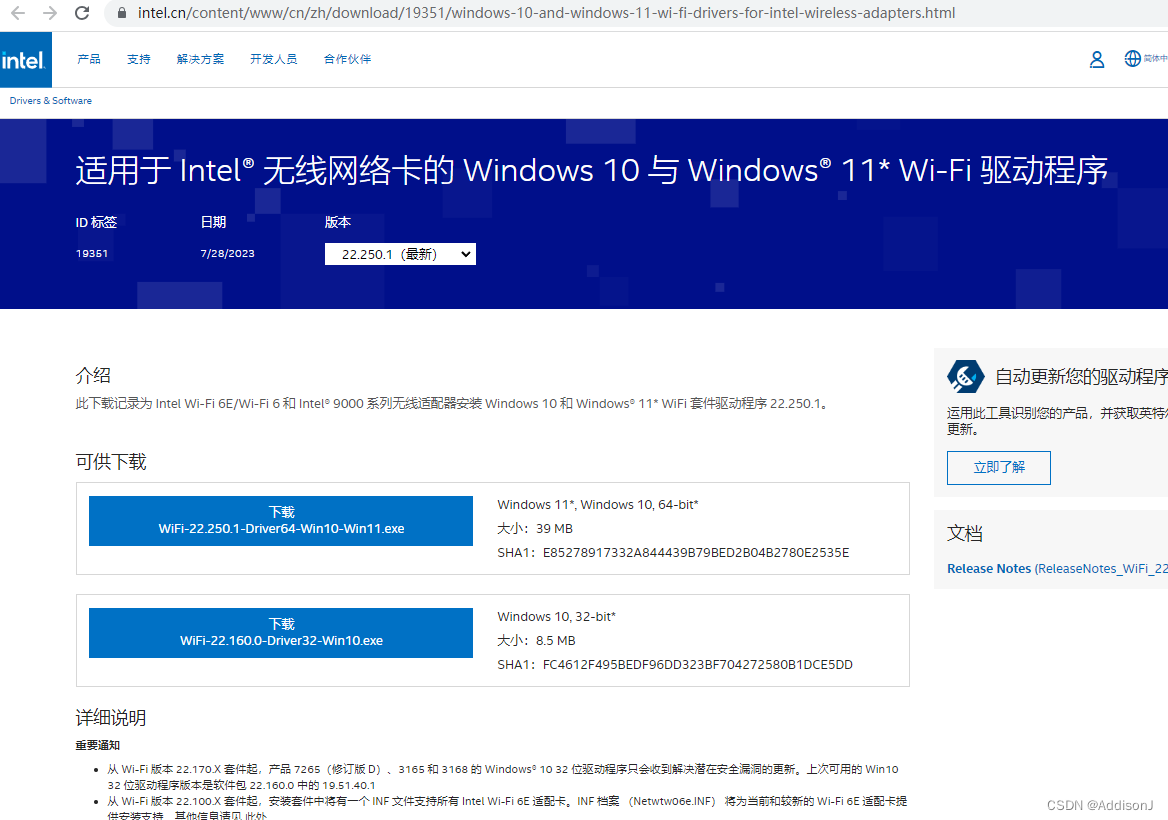
安装好后就可以搜索到这个wifi6无线路由器信号了
相关文章:

笔记本电脑搜索不到wifi6 无线路由器信号
路由器更换成wifi6 无线路由器后,手机能搜索到这个无线信号,但是笔记本搜索不到这个无线信号,后网上搜索后发现是无线网卡驱动问题,很多无线网卡使用的是Intel芯片,Intel就此发布了公告,升级驱动就可以彻底…...

js获取input?
在JavaScript中,获取输入框(通常指的是HTML的<input>元素)的值有多种方法。以下是其中的一些: 通过ID获取: javascriptvar inputValue document.getElementById(inputId).value; 这里,inputId 是…...
STM32 CAN使用
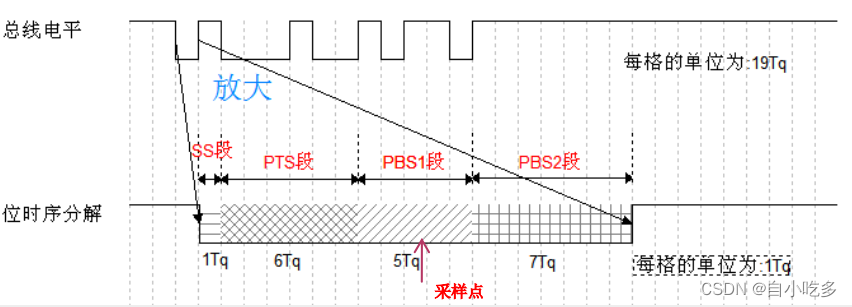
STM32 CAN使用 简介各种通讯接口对比报文总线上的报文信息表示为几种固定的赖类型数据帧列表模式掩码模式配置CAN配置参数位时序 简介 控制器局域网CAN(Controller Area Network)是由德国博世公司为汽车应用而开发的多主机局部网络,用于汽车的监测和控制…...

安全和便捷:如何将运营商二要素API应用于实名制管理中
引言 随着互联网的快速发展,数字化身份验证和实名制管理变得越来越重要。在金融、电子商务、社交媒体等领域,确保用户身份的安全和准确性至关重要。运营商二要素核验API成为了实名制管理的有力工具,它不仅能够提供高水平的安全性,…...
leetcode-二叉树
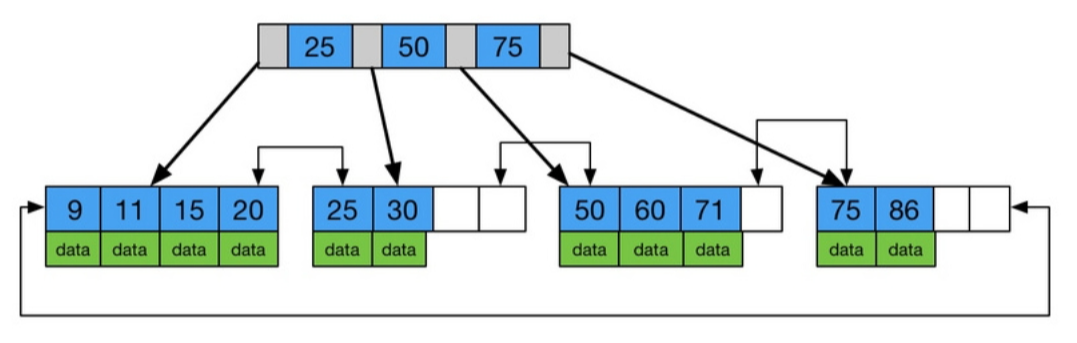
B树和B树的区别 B树,也即balance树,是一棵多路自平衡的搜索树。它类似普通的平衡二叉树,不同的一点是B树允许每个节点有更多的子节点。 B树内节点不存储数据,所有关键字都存储在叶子节点上。B树: B树: 二叉…...
【鸿蒙软件开发】ArkTS基础组件之TextTimer(文本显示计时)、TimePicker(时间选择)
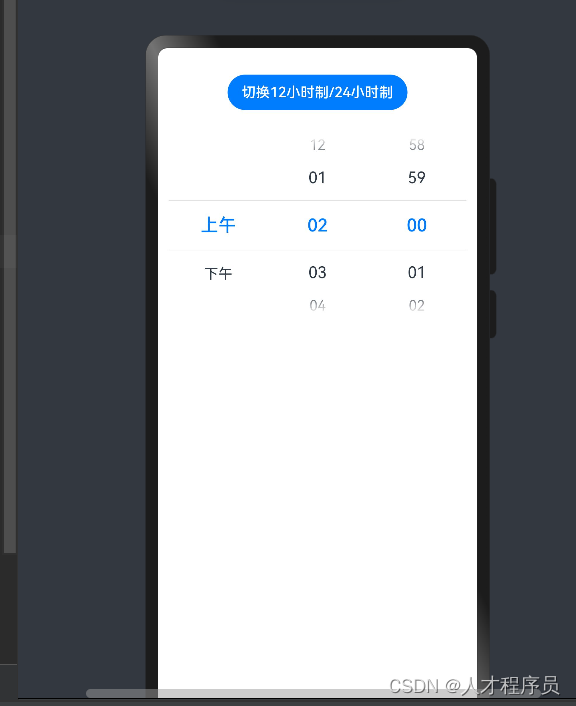
文章目录 前言一、TextTimer1.1 子组件1.2 接口参数TextTimerController 1.3 属性1.4 事件1.5 示例代码 二、TimePicker2.1 子组件2.2 接口参数 2.3 属性2.4 事件TimePickerResult对象说明 2.5 示例代码 总结 前言 通过文本显示计时信息并控制其计时器状态的组件。 时间选择组…...

pytorch 笔记:KLDivLoss
1 介绍 对于具有相同形状的张量 ypred 和 ytrue(ypred 是输入,ytrue 是目标),定义逐点KL散度为: 为了在计算时避免下溢问题,此KLDivLoss期望输入在对数空间中。如果log_targetTrue,则目标…...
父子项目打包发布至私仓库
父子项目打包发布至私仓库 1、方法一 在不需要发布至私仓的模块上添加如下代码: <plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-deploy-plugin</artifactId><configuration><skip>true</s…...

汽车网络安全--ECU的安全更新
目前,汽车ECU的软件更新可以总结分成三大类: 工厂刷写模式:工厂大批量刷写或者升级,一般在出厂用; 工程模式:4S店、工厂等专业人员进行的ECU固件更新,通常是动力、转向、车控等; 车主模式:车主根据云端推送信息,通过IVI进行应用软件更新;目前也有趋势通过这种方式刷…...

NLP之搭建RNN神经网络
文章目录 代码展示代码意图代码解读知识点介绍1. Embedding2. SimpleRNN3. Dense 代码展示 # 构建RNN神经网络 from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, SimpleRNN, Embedding import tensorflow as tfrnn Sequential() …...

Android问题笔记四十三:JNI 开发如何快速定位崩溃问题
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
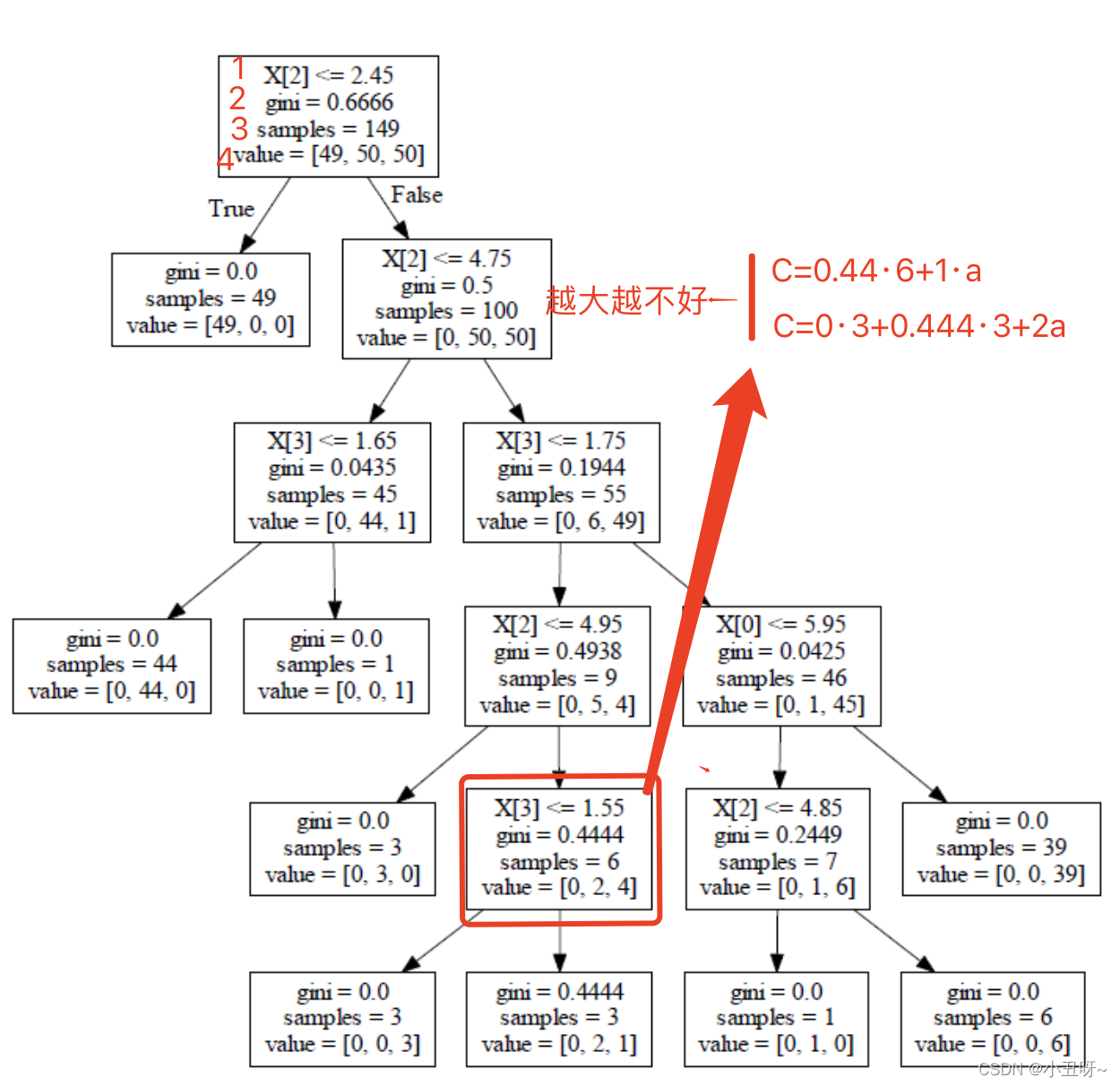
机器学习 | 决策树算法
一、决策树算法概述 1、树模型 决策树:从根节点开始一步步走到叶子节点(决策)。所有的数据最终都会落到叶子节点,既可以做分类也可以做回归。 在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合࿰…...

javascript中各种风骚的代码
1.判断数值符号是否相同 function numericSymbolsIsEqual(x: number, y: number): boolean {return (x ^ y) > 0}console.log(numericSymbolsIsEqual(1, 1))console.log(numericSymbolsIsEqual(-1, 1))console.log(numericSymbolsIsEqual(1, -1))console.log(numericSymbols…...

el-tree横向纵向滚动条
el-tree未展开时样式 el-tree展开时样式 给容器一个高度,然后样式加上overflow: scroll,这样纵向滚动条就出来了。 <el-card style"height: 528px;overflow: scroll"><el-inputplaceholder"输入关键字进行过滤"v-model&…...

STM32G030F6P6 芯片实验 (一)
STM32G030F6P6 芯片实验 (一) 淘宝搞了几片, 没试过 G系列, 试试感觉. 先搞片小系统版: 套 STM32F103C8T6小系统板格式. 原理图: (1) Ref 有点跳, 从 STM32F103C8T6 系统板改的, 没重编号. (2) Type-C 纯给电, 砍了 16pin的, 直接换 6pin的。 (3) 测试LED放 B2。 (4) 测试底…...
Wpf 使用 Prism 实战开发Day01
一.开发环境准备 1. VisualStudio 2022 2. .NET SDK 7.0 3. Prism 版本 8.1.97 以上环境,如有新的版本,可自行选择安装新的版本为主 二.创建Wpf项目 1.项目的名称:MyToDo 项目名称:这里只是记录学习,所以随便命名都无所谓,只要觉得合理就…...

6G关键新兴技术- 智能超表面(RIS)技术演进
摘要: 根据欧盟5G公私联盟协会定义,可重构智慧表面技术是由能够任意塑造电磁波面的材料组成,几乎是被动设备,可以适应或改变发射器和接收器之间的无线电信号。 一、产品定义及范围 根据欧盟5G公私联盟协会(5G Infrastructure P…...
【redhat9.2】搭建Discuz-X3.5网站
步骤 1.配置软件仓库 2.安装对应的软件 httpd php* mariadb* 3.启动服务 httpd mariadb 4.配置数据库 创建数据库 修改root密码 数据库的 5.传源码包(Discuz-X3.5) 解压 6.web页面初始化 关闭防火墙 允许http服务通过 修改权限 实…...

算法篇 : 并查集
介绍 英文名:union find set 作用:合并集合,查询集合 合并:将有直接关系的顶点放在一个集合里面 查找:查询某个顶点所属的集合 集合的标志:用祖先点的标号作为每个集合的标识 案例 如果说将下图的集合2合并…...

AM@微积分基本定理@微积分第二基本定理
文章目录 abstract微积分第二基本定理微积分基本公式公式书写例 结合不定积分的方法求定积分定积分换元法证明 定积分换元公式逆用例 和不定积分第二类换元法的差别定积分分部积分法例 abstract 微积分第一基本定理告诉我们,总是能够通过积分法构造(表达)一个连续函数的原函数…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
