【电路笔记】-交流电阻和阻抗
交流电阻和阻抗
文章目录
- 交流电阻和阻抗
- 1、概述:电阻率
- 2、交流状态与直流状态近似性
- 3、交流状态与直流状态的差异性
- 3.1 趋肤效应(The Skin Effect)
- 3.2 靠近效应(The Proximity Effect)
- 4、总结
电阻是一种特性,用于表征当电压差施加到其端子时,特定组件如何对电流产生阻力。 在本文中,我们将重点关注施加交流电压时电阻器产生的阻力。
在第一部分中,为了进一步了解欧姆定律,我们做了一个简单的演示,详细介绍了电阻和电阻器组件的概念。 我们将在第二节中看到交流状态和直流状态下的电阻之间的行为相似性。
剩余的部分将重点介绍导致电阻器的交流和直流电阻之间存在差异的两种现象,特别是当频率增加时。
1、概述:电阻率
在本节中,我们将更清楚地定义阻力是什么以及它取决于什么。 正如标题所示,主要概念称为电阻率。 让我们考虑一种横截面为 A、长度为 L、具有两个端子的平行六面体材料,如图 1 所示:

电阻率 ρ \rho ρ 以 Ω . m \Omega.m Ω.m 表示,它是材料的固有属性。 这意味着电阻率不依赖于几何形状。 任何材料的电阻率值都可以轻松地在在线表格或书籍中找到。
此外,电阻率是罕见的变化如此之多的数量级的物理量之一。 例如,铜是电阻较小的材料之一,其电阻率为 ρ c o p p e r = 1.7 × 10 − 8 Ω . m \rho_{copper}=1.7×10-8\Omega.m ρcopper=1.7×10−8Ω.m。 另一方面,特氟龙是电阻率最高的材料之一,电阻率 ρ T e f l o n > 1 0 23 Ω . m \rho_{Teflon}>10^{23} \Omega.m ρTeflon>1023Ω.m。
对于特定的几何形状,如图 1 所示,电阻率和电阻 R R R通过公式1中给出的以下公式联系起来:

我们可以用这个公式来理解电阻如果受到几何形状和材料固有电阻率的影响:
- 如果长度增加,电子必须穿过电阻更大的材料,因此电阻增加。
- 如果横截面减小,电子可用的路径就会减少(例如简单的道路或 4 车道高速公路),因此电阻会增加。
- 如果电阻率增加,则材料本质上电阻更大,因此电阻再次增加。
电阻器通常由陶瓷或碳粉制成,电阻率为 ρ c a r b o n ≅ 10 − 3 Ω . m \rho_{carbon}≅10-3\Omega.m ρcarbon≅10−3Ω.m。 例如,如果我们选择比率 L / A = 1000 L/A=1000 L/A=1000,我们会得到几欧姆的电阻。
2、交流状态与直流状态近似性
在直流状态下,电阻器产生的电阻非常容易描述,可以用欧姆定律来描述。 电压 V 和电流 I 之间存在线性关系,其中这两个量通过称为电阻的因子 R R R 联系起来,例如 U = R × I U=R×I U=R×I。

那么,如果我们将图 2 中的直流电源替换为交流电源,会发生什么情况呢? 欧姆定律仍然适用吗?
答案很简单,在正常的频率和幅度(不太高)条件下,电阻器的行为与直流状态下完全相同。 因此,电阻的复阻抗是实数 Z = R + j × 0 = U / I Z=R+j×0=U/I Z=R+j×0=U/I。
在直流状态下,加热产生的功率由电压和电流的乘积给出: P = U × I P=U×I P=U×I。 对于瞬时功率的交流状态也是如此: P ( t ) = U ( t ) × I ( t ) P(t)=U(t)×I(t) P(t)=U(t)×I(t)。 然而,焦耳加热所消耗的平均功率 P a v g P_{avg} Pavg 更值得关注。 P a v g P_{avg} Pavg的公式如下面的公式 2 所示,其中 ϕ \phi ϕ 表示电压和电流之间的相移:

由于电阻的阻抗是实数,我们可以参考复数教程来理解相移Φ等于0。 下标“RMS”表示均方根,其定义在交流波形和交流电路理论有完整解释。
对于纯电阻电路的特殊情况,平均功率的表达式因此简化为 P a v g = U R M S × I R M S P_{avg}=U_{RMS}×I_{RMS} Pavg=URMS×IRMS。
3、交流状态与直流状态的差异性
我们在最后一节中指出了当交流电源的频率大幅增加时,与直流电阻相比,交流电阻会发生变化的两种效应。 本节分为两个小节来独立处理这些现象。
3.1 趋肤效应(The Skin Effect)
在谈论这个现象之前,我们需要先了解一下它的起源。 第一个效应是由于我们在交流波形和交流电路理论中提到的电磁感应定律造成的。
感应定律或楞次定律指出,考虑到可变磁场 B 1 ( t ) B_1(t) B1(t) 穿过的闭合电路 C C C,会产生电流 I I I,以产生相反的磁场 B 2 ( t ) B_2(t) B2(t),以缓和 B 1 ( t ) B_1(t) B1(t)的变化。

这种电磁效应广泛存在于许多技术中,并且可以以不同的方式使用,这就是电感器、涡轮机、变压器或电磁炉的工作原理。
现在让我们回到如图1所示的电阻材料。与交变磁场生成电流环路的方式相同,交变电流 I ( t ) I(t) I(t) 也会生成磁环 B ( t ) B(t) B(t)。 由于磁环是在电阻材料内生成的,因此会产生如图3所示的电流环。 这些电流环路有一个特定的名称:它们被称为涡流(Eddy Currents)或傅科电流( Foucault Currents)。

此类电流集中在电阻材料的边界处,如上图 4 所示。 当交流电 I ( t ) I(t) I(t) 的频率增加时,这种称为集肤效应的现象往往变得更加重要。
描述趋肤效应的最重要参数称为趋肤深度,并记为 δ \delta δ。 它表示从大部分涡流集中的电阻材料边界开始的厚度。
该值与 1 / f 1/\sqrt f 1/f 成正比,其中 f f f 是频率。 因此,增加频率往往会减少趋肤深度。 当交流电的频率变得非常高时,大部分电流位于电阻材料边界附近的小区域内,如图 5 所示:

材料的有效横截面 A 变得更小,因此,根据公式1,电阻增加。
对于特定的频率值(取决于材料),与直流电阻相比,集肤效应倾向于增加交流电阻: R A C > R D C R_{AC}>R_{DC} RAC>RDC。
3.2 靠近效应(The Proximity Effect)
电磁感应也是另一种称为靠近效应的效应的原因,这种效应会极大地影响电路的交流电阻。 当两个或多个附近的导体承载电流时,就会观察到靠近效应。
为了简单起见,我们考虑两条平行电线 W 1 W_1 W1 和 W 2 W_2 W2 承载相同的交流电流 I(t)。 如果电流的频率足够高, W 1 W_1 W1(也由 W 2 W_2 W2,但未在图 6 中表示)将在自身周围产生磁环 B ( t ) B(t) B(t)。 如果导线足够近,磁环将穿过第二根导线并在 W 2 W_2 W2 中产生涡流(如前所述):

由于效果是对称的, W 2 W_2 W2 也会在 W 1 W_1 W1中感应出涡流。 对于本例,当前浓度分布如下图7 所示:

例如,对于趋肤效应,靠近效应是电阻材料内电流分布改变的结果,这种改变往往会通过减小有效横截面来增加电阻。 当频率增加时,这种效应也会增强,并可能导致交流电阻和直流电阻之间出现一个或多个数量级的差异。
4、总结
本文重点讨论直流和交流状态下电阻材料的电阻值之间的相似性和差异。
- 首先,我们通过介绍电阻率的概念来介绍电阻到底由什么组成。 我们已经看到,电阻取决于这种固有属性以及所考虑材料的几何形状。
- 在第二部分中,我们研究正常工作条件(频率不太高)下的交流电阻。 欧姆定律可以应用于交流电制,例如直流电制。 此外,由于没有观察到相移,因此功率的表达式与使用电压和电流量的 RMS 值的直流状态相似。
- 在上一节中,两个现象指出了这样一个事实:当频率增加时,交流电阻会比直流电阻高得多。
- 第一种效应称为趋肤效应,是由于导体边界附近电流的重新分布造成的。 这会减小电流通过的有效横截面,从而增加电阻。
- 第二个效应是靠近效应,当两个附近的导体同时承载频率足够高的交流电时,就会发生这种效应。 它还会导致靠近其边界之一的两个导体内的电流重新分布,这与趋肤效应类似,会增加电线的电阻。
- 然而,只有当频率非常高时,这些效应才会开始对电路产生很大影响。 例如,在 50 Hz 时,铜线的半径不需要宽于 8 毫米,因为该频率下的集肤深度约为 9 毫米。 在 10 MHz 时,该深度变为约 21 μm,这对于宽度可降至 10 μm 的印刷电路板 (PCB) 来说仍然不是设计问题。 我们可以说,在 100 MHz 以上,与该深度相关的趋肤效应和靠近效应会限制正确设计电路。
相关文章:

【电路笔记】-交流电阻和阻抗
交流电阻和阻抗 文章目录 交流电阻和阻抗1、概述:电阻率2、交流状态与直流状态近似性3、交流状态与直流状态的差异性3.1 趋肤效应(The Skin Effect)3.2 靠近效应(The Proximity Effect) 4、总结 电阻是一种特性,用于表征当电压差施…...
android开发使用OkHttp自带的WebSocket实现IM功能
一、背景 android app开发经常会有IM需求,很多新手不晓得如何入手,难点在于通讯不中断。其实android发展到今天,很多技术都很完善,有很多类似框架可以实现。例如有:okhttp自带的websocket框架、easysocket等等。本文主…...

前端小技巧: TS实现柯里化函数
实现 curry 函数,把其他函数柯里化 curry 返回一个函数fn执行fn, 中间状态返回函数,如 add(1), 或者 add(1)(2)最后返回执行结果,如 add(1)(2)(3) function curry(fn:Function) {const fnArgsLen fn.length // 传入函数的参数长度let args…...

【算法-数组2】有序数组的平方 和 长度最小的子数组
今天,带来数组相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 有序数组的平方 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输…...

H5游戏源码分享-接苹果游戏拼手速
H5游戏源码分享-接苹果游戏拼手速 看看在20秒内能接多少个苹果 <html> <head><title>我是你的小苹果</title><meta charset"utf-8"/><meta name"viewport" content"initial-scale1, user-scalableno, minimum-scale…...
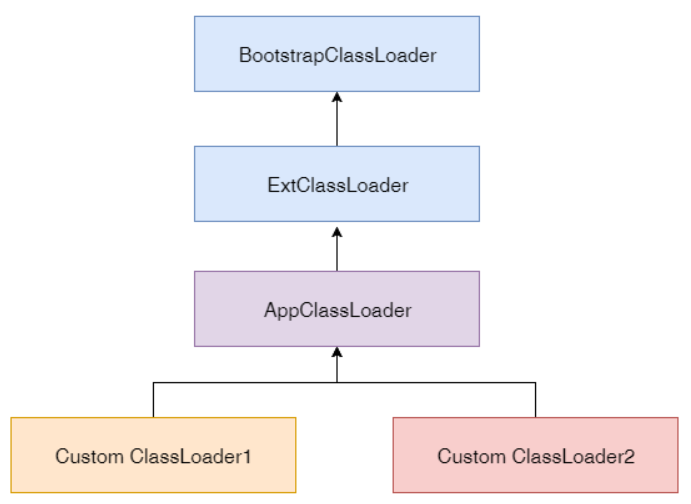
详解类生到死的来龙去脉
类生命周期和加载过程 一个类在 JVM 里的生命周期有 7 个阶段,分别是加载(Loading)、校验(Verification)、准备(Preparation)、解析(Resolution)、初始化(Ini…...
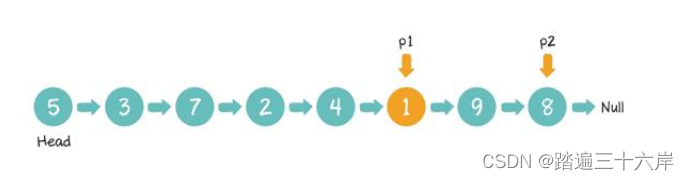
寻找倒数第K个节点
这篇文章也是凑数的 ... 寻找倒数第K个节点 描述 : 找出单向链表中倒数第 k 个节点。返回该节点的值。 题目 : LeetCode 返回倒数第K个节点 : 面试题 02.02. 返回倒数第 k 个节点 说明 : 给定的 k 保证是有效的。 分析 : 我们给出个例子 : 首先,我们创建两个…...
)
[ROS系列]ubuntu 20.04 从零配置orbslam3(无坑版)
目录 背景: 结果展示: 一、配置虚拟机 二、 同步网络时间 三、ping网络 四、 安装ros 五、下载源码 六、下载orb_slam3 error1:Pangolin error2: ./HelloPangolin: error while loading shared libraries: libpango_windowing.so: cannot open shared object file…...

网络协议--TCP的保活定时器
23.1 引言 许多TCP/IP的初学者会很惊奇地发现可以没有任何数据流通过一个空闲的TCP连接。也就是说,如果TCP连接的双方都没有向对方发送数据,则在两个TCP模块之间不交换任何信息。例如,没有可以在其他网络协议中发现的轮询。这意味着我们可以…...
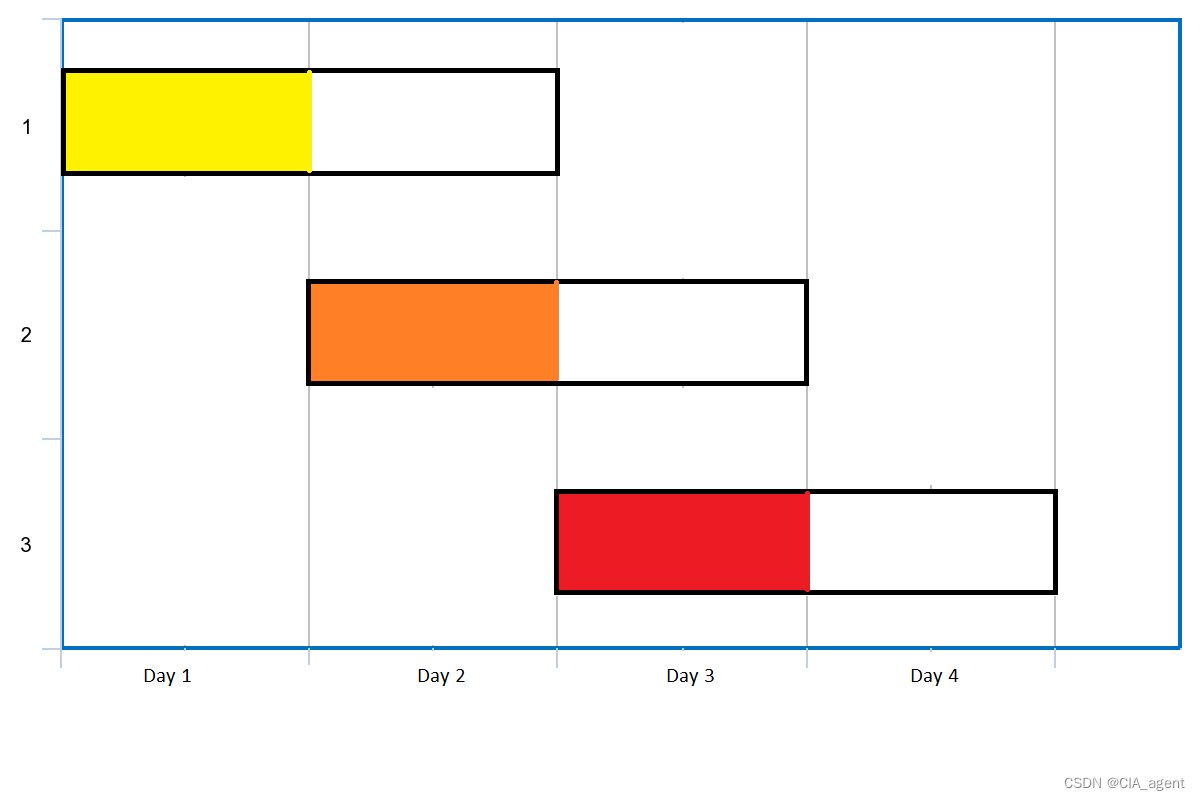
leetcode 1353. 最多可以参加的会议数目
给你一个数组 events,其中 events[i] [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。 你可以在满足 startDayi < d < endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。 请你返回…...
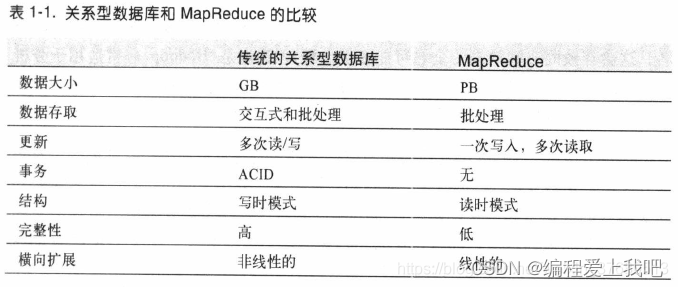
hadoop权威指南第四版
第一部分 HaDOOP基础知识 1.1 面临的问题 存储越来越大,读写跟不上。 并行读多个磁盘。 问题1 磁盘损坏 – 备份数据HDFS 问题2 读取多个磁盘用于分析,数据容易出错 --MR 编程模型 1.2 衍生品 1 在线访问的组件是hbase 。一种使用hdfs底层存储的模型。…...

LeetCode75——Day20
文章目录 一、题目二、题解 一、题目 2215. Find the Difference of Two Arrays Given two 0-indexed integer arrays nums1 and nums2, return a list answer of size 2 where: answer[0] is a list of all distinct integers in nums1 which are not present in nums2. an…...

搭建微信小程序环境及项目结构介绍
一、注册 访问微信公众平台,将鼠标的光标置于账号分类中的小程序上, 点击‘查看详情’ 点击“前往注册” 下方也可以点击注册: 小程序注册页面: 步骤a:进入小程序注册页,根据指引填写信息和提交相应的资料&#x…...
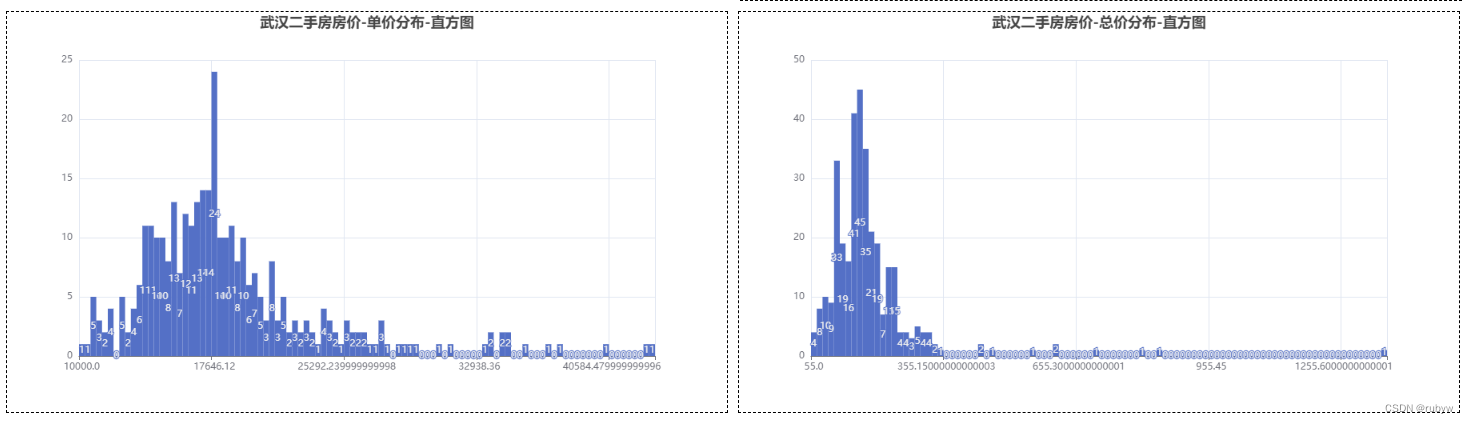
Python通过pyecharts对爬虫房地产数据进行数据可视化分析(一)
一、背景 对Python通过代理使用多线程爬取安居客二手房数据(二)中爬取的房地产数据进行数据分析与可视化展示 我们爬取到的房产数据,主要是武汉二手房的房源信息,主要包括了待售房源的户型、面积、朝向、楼层、建筑年份、小区名称…...
关于测试组件junit切换testng的示例以及切换方式分享
文章目录 概要首先看看junit和testng的区别实践篇摸拟业务逻辑代码简单对象数据层摸拟类业务逻辑层摸拟类后台任务摸拟类 基于springmockjunit基于springmocktestng 示例的差异点junit与testng的主要变动不大,有以下几个点需要注意注解部分在before,after中testng多出按配置执行…...

nginx 内存管理(二)
共享内存 共享内存结构与接口定义nginx共享内存在操作系统上的兼容性设计互斥锁锁的结构体锁的一系列操作(core/ngx_shmtx.c)创建锁 原子操作nginx的上锁操作尝试加锁获取锁释放锁强迫解锁唤醒等待进程 slab共享内存块管理nginx的slab大小规格内存池结构…...

【DevChat】智能编程助手 - 使用评测
写在前面:博主是一只经过实战开发历练后投身培训事业的“小山猪”,昵称取自动画片《狮子王》中的“彭彭”,总是以乐观、积极的心态对待周边的事物。本人的技术路线从Java全栈工程师一路奔向大数据开发、数据挖掘领域,如今终有小成…...
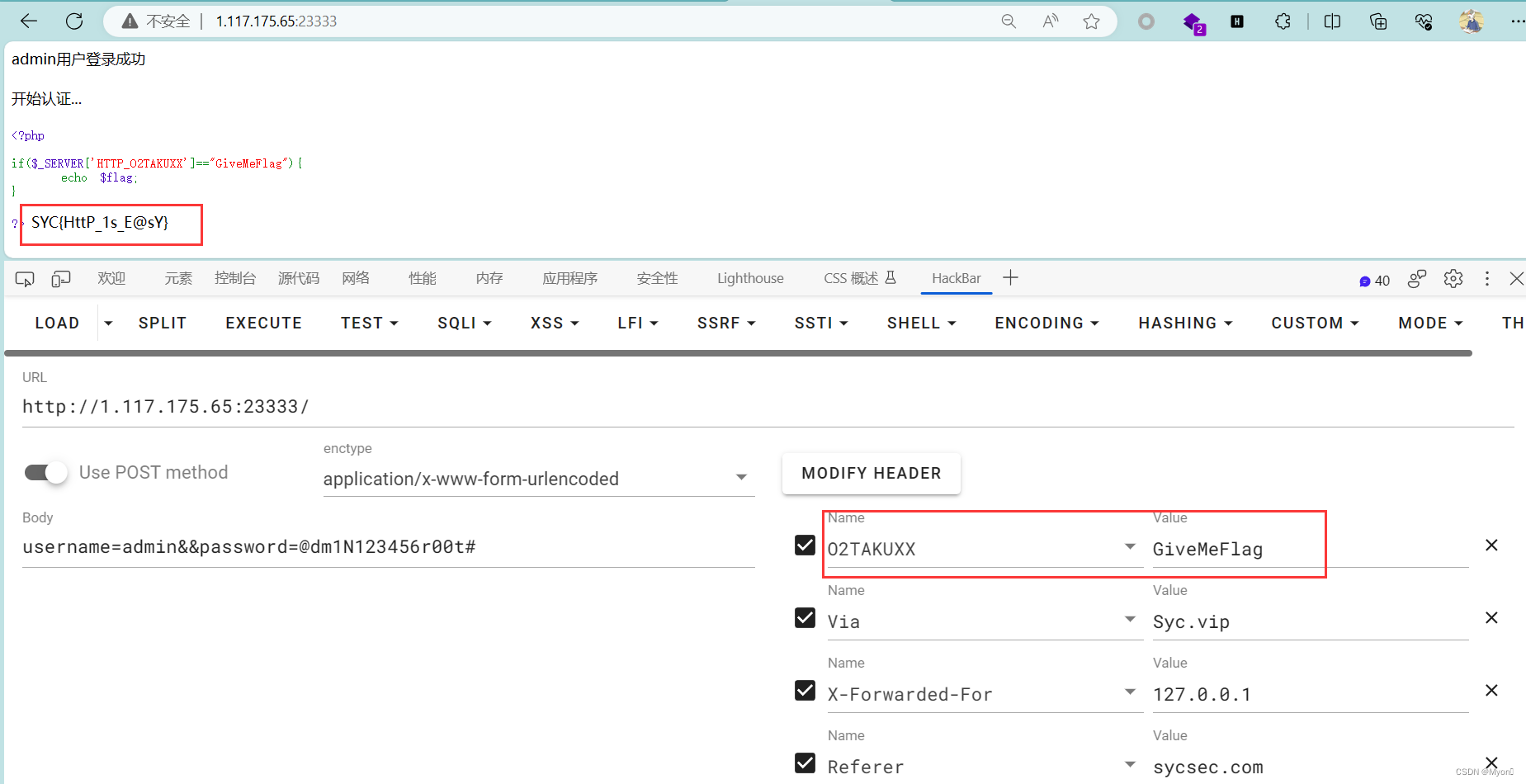
Geek challenge 2023 EzHttp
打开链接需要使用post请求提交username和password 查看源码得到提示,爬虫想到robots协议 访问robots.txt 访问得到的路径:/o2takuXXs_username_and_password.txt 拿到用户名和密码: username:admin password:dm1N123456r00t# 进行post传参…...
matlabR2021a正版免费使用
目录 matlab介绍: 安装: matlab介绍: MATLAB(Matrix Laboratory的缩写)是一种高级技术计算和编程环境,由MathWorks公司开发。它在科学、工程、数据分析和数学建模领域中广泛应用,为用户提供了…...
天气数据可视化平台-计算机毕业设计vue
天气变幻无常,影响着我们生活的方方面面,应用天气预报信息可以及时了解天气的趋势,给人们的工作、生活等带来便利,也可以为我们为未来的事情做安排和打算,所以一个精准的、易读 通过利用 程序对气象网站大量的气象信息…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
