82.二分查找
目录
什么是二分查找
一、左闭右闭写法[left,right]
代码演示:
二、左闭右开写法[left,right]
代码演示:
今天进行了二分查找的学习。
什么是二分查找
二分查找(Binary Search)是一种常用的搜索算法,也被称为折半查找。它用于在已排序的数组中查找特定元素的位置,通过反复将待查找范围缩小为一半来提高效率。
以下是二分查找的一般步骤:
确定搜索范围:首先,确定要搜索的数组的起始和结束位置。通常,这是整个数组的起始和结束。
计算中间位置:计算中间位置的索引,即 (start + end) / 2。
比较中间元素:将要查找的元素与中间位置的元素进行比较。
- 如果要查找的元素等于中间位置的元素,那么找到了目标,返回中间位置的索引。
- 如果要查找的元素小于中间位置的元素,那么说明目标在左半部分,将搜索范围缩小为左半部分。
- 如果要查找的元素大于中间位置的元素,那么说明目标在右半部分,将搜索范围缩小为右半部分。
重复步骤2和步骤3,直到找到目标元素或搜索范围为空。如果搜索范围为空,说明目标元素不在数组中。
二分查找的时间复杂度为O(log n),其中n是数组的长度。这是因为每次迭代都将搜索范围缩小为一半,所以在最坏情况下,需要进行log n次迭代才能找到目标元素。
二分查找通常用于已排序的数组,例如升序排列的整数数组或字母表中的单词。它是一种高效的查找算法,适用于大型数据集。
一、左闭右闭写法[left,right]
定义target是在区间[left,right]里面的,所以有如下两点:middle=(left+right)/2;
- while( left <= right ),应该使用<=,因为是一个左闭右闭的区间。例:[1,1],此时while循环应当用<=.
- if( nums[middle] > target ),此时right应该赋值为middle-1;因为当前这个nums[middle]⼀定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
代码演示:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0; // 定义左边界int right = nums.size() - 1; // 定义右边界while (left <= right) {int middle = left + (right - left) / 2; // 计算中间位置,避免整数溢出if (nums[middle] == target) {return middle; // 找到目标,返回索引} else if (nums[middle] > target) {right = middle - 1; // 目标在左半部分,更新右边界} else {left = middle + 1; // 目标在右半部分,更新左边界}}return -1; // 如果未找到目标元素}
};
在计算中间位置时,一种最直观的方法是使用
(left + right) / 2。然而,这种方式在极端情况下,当left和right很大时,可能会导致整数溢出问题,这会导致程序错误。为了避免整数溢出,我们使用了
(right - left) / 2,而不是(left + right) / 2来计算中间位置。这样做的原因是,(right - left)表示了左边界和右边界之间的距离,然后除以2,得到的结果就是中间位置相对于左边界的偏移量。这个偏移量被加到左边界上,从而得到中间位置。这种方式确保了中间位置的计算不会导致整数溢出,因为它始终处理整数边界的相对偏移量,而不是绝对值。这在处理大数组时特别重要,以确保算法的正确性。
二、左闭右开写法[left,right]
定义 target 是在⼀个在左闭右开的区间⾥,也就是[left, right) ,那么二分法的边界处理⽅式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下⼀个查询区间不会去比较nums[middle],
代码演示:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0; // 定义左边界int right = nums.size(); // 定义右边界,注意这里是 nums.size(),不再减1while (left < right) {int middle = left + (right - left) / 2; // 计算中间位置,避免整数溢出if (nums[middle] == target) {return middle; // 找到目标,返回索引} else if (nums[middle] > target) {right = middle; // 目标在左半部分,更新右边界,不再减1} else {left = middle + 1; // 目标在右半部分,更新左边界}}return -1; // 如果未找到目标元素}
};
写在最后:以上就是本篇文章的内容了,感谢你的阅读。如果感到有所收获的话可以给博主点一个赞哦。如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~
tips:学于代码随想录
相关文章:

82.二分查找
目录 什么是二分查找 一、左闭右闭写法[left,right] 代码演示: 二、左闭右开写法[left,right] 代码演示: 今天进行了二分查找的学习。 什么是二分查找 二分查找(Binary Search)是一种常用的搜索算法,也被称为折…...
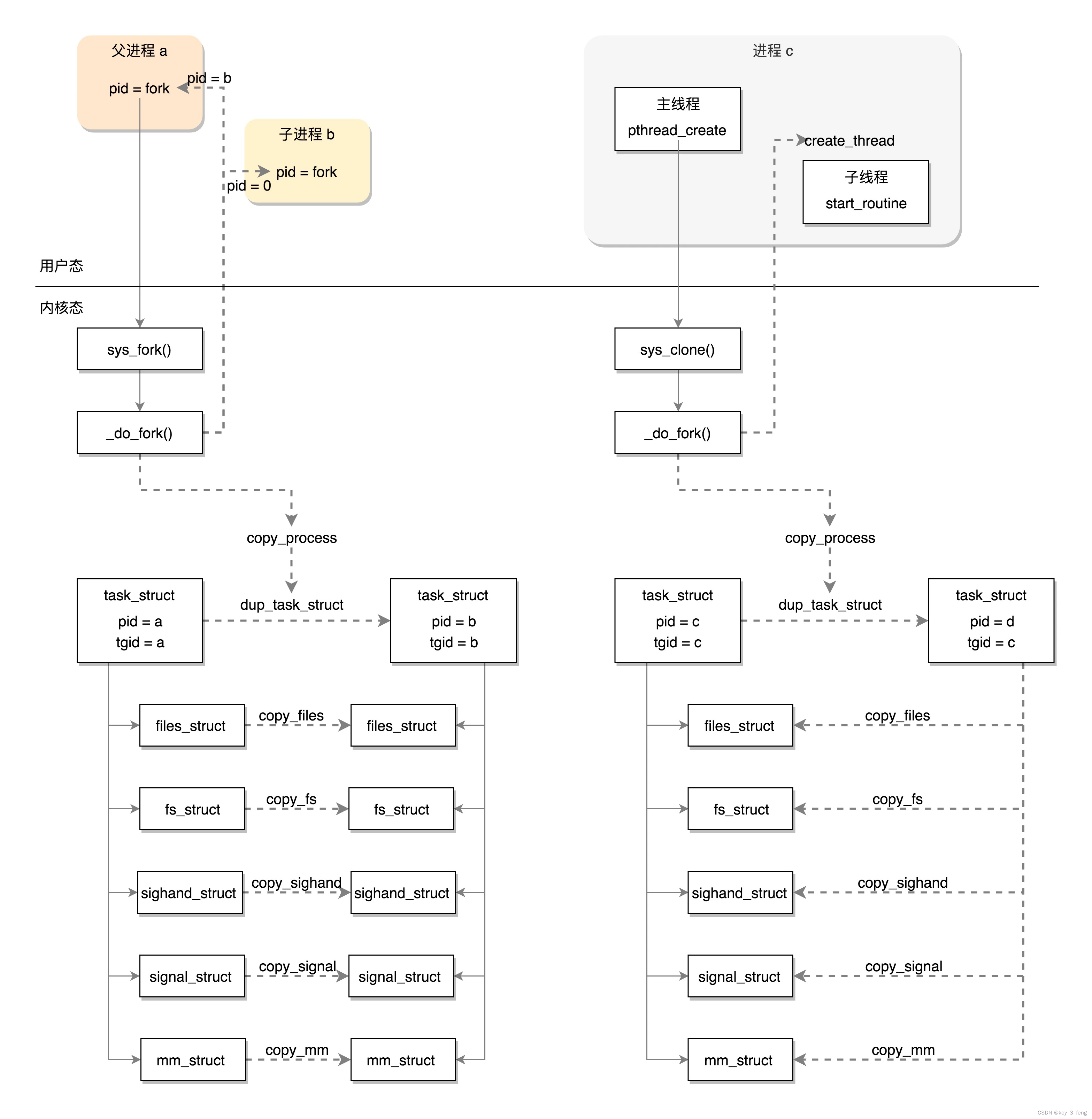
线程是如何创建的
线程不是一个完全由内核实现的机制,它是由内核态和用户态合作完成的。pthread_create 不是一个系统调用,是 Glibc 库的一个函数,所以我们还要去 Glibc 里面去找线索。 首先处理的是线程的属性参数。例如前面写程序的时候,我们设置…...

owl_vit安装步骤
owl项目的clip目录与openai的clip重名了,import时容易找不到文件simple_tokenizer。 from clip import simple_tokenizer解决办法: 把clip项目下的simple_tokenizer.py拷贝到owl项目下的clip文件夹 cp simple_tokenizer.py /{project_dir}/scenic/scenic/projects…...

运行real.exe时出现NUM_METGRID_SOIL_LEVELS=0
本人在运行real.exe时,发现出现这样的报错: d01 2020-01-01_00:00:00 ---- ERROR: Mismatch between namelist and global attribute NUM_METGRID_SOIL_LEVELS NOTE: 2 namelist vs input data inconsistencies found. -------------- FATAL CALL…...

【数值计算方法】Gauss消元法及其Python/C实现
文章目录 一、基础理论1. 线性方程组2. Gauss消元法的详细步骤3. 注意事项 二、具体计算过程1. 用Gauss 消元法求A的LU分解,并由此求解方程组 Ax ba. 将A进行LU分解。b. 使用LU分解求解方程组Axb 三、代码实现1. Python代码实现2. C语言代码实现 Gauss消元法&#x…...

ins老被封禁?快来看看这些雷区你踩了没!
做外贸的小伙伴应该都运营或者接触过Instagram,但是忽视平台规则和操作不当很容易出现ins被封号的情况,今天就给大家介绍ins封禁原因,大家在运营过程中就可以很好避免了! Instagram 封禁原因 1.短时间内大量关注和点赞操作 为了封…...
)
《Effective Java》读书笔记(1-2章)
第一章 创建和销毁对象 1. 考虑用静态代替构造方法 想要获取一个类的实例,一种传统的方式是通过共有的构造器,当然还可以使用另一种技术:提供共有的静态工厂方法。 什么是静态工厂? public static Boolean valueOf(boolean b) …...
函数)
C++版split(‘_‘)函数
目录 1 使用stringstream2 使用双指针算法 1 使用stringstream #include <iostream> #include <sstream> #include <string> #include <vector>using namespace std;vector<string> split(string str, char separator) {vector<string> …...

Leaky singletons的一种使用场景
Leaky singletons的一种使用场景 文章目录 Leaky singletons的一种使用场景场景问题本质如何解决Leaky singletons 场景 最近遇到了这个问题,正好想记录下。 比如你有一段代码,如下(伪代码): static std::map<int…...

TensorFlow图像多标签分类实例
接下来,我们将从零开始讲解一个基于TensorFlow的图像多标签分类实例,这里以图片验证码为例进行讲解。 在我们访问某个网站的时候,经常会遇到图片验证码。图片验证码的主要目的是区分爬虫程序和人类,并将爬虫程序阻挡在外。 下面…...

Python程序设计期末复习笔记
文章目录 一、数据存储1.1 倒计时1.2 os库1.3 字符串操作1.4 文件操作1.5 列表操作1.6 元组1.7 字典 二、文本处理及可视化2.1 jieba分词2.2 集合操作2.3 pdf文件读取2.4 参数传递2.5 变量作用域 三、数据处理分析3.1 Sumpy3.2 Matplotlib3.3 Numpy 四、Pandas4.1 索引操作4.2 …...

人大与加拿大女王大学金融硕士—与您共创辉煌
生活的本质就是有意识的活着,而生活的智慧就是活出了自己想要的样子,那些真正厉害的人,从来都在默默努力,伴随着金融人才的需求日益增长,中国人民大学与加拿大女王大学联合推出了人大女王金融硕士项目,旨在…...
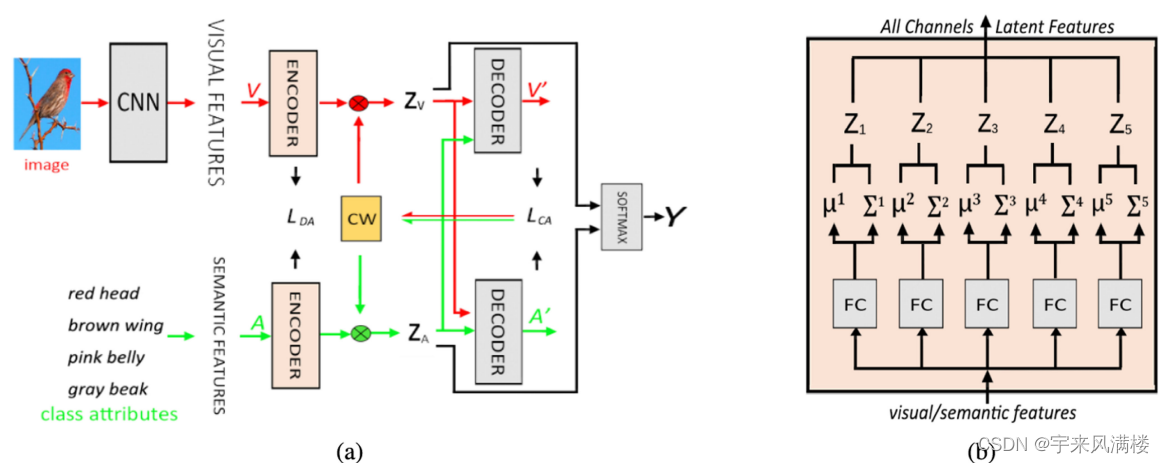
Generalized Zero-Shot Learning With Multi-Channel Gaussian Mixture VAE
L D A _{DA} DA最大化编码后两种特征分布之间的相似性 辅助信息 作者未提供代码...
)
10.30 知识总结(标签分类、css介绍等)
一、 标签的分类 1.1 单标签 img br hr <img /> 1.2 双标签 a h p div <a></a> 1.3 按照标签属性分类 1.3.1 块儿标签 即自己独自占一行 h1-h6 p div 1.3.2 行内(内联)标签 即自身文本有多大就占多大 a span u i b s 二、 标签的嵌套 标签之间是可以互相…...
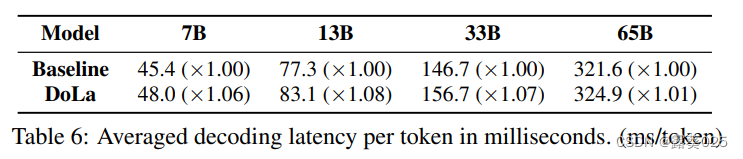
DoLa:对比层解码提高大型语言模型的事实性
DoLa:对比层解码提高大型语言模型的事实性 摘要1 引言2 方法2.1 事实知识在不同层级上演化2.2 动态早期层选择2.3 预测对比 3 实验3.1 任务3.2 实验设置3.3 多项选择3.3.1 TruthfulQA:多项选择3.3.2 FACTOR:维基、新闻 3.4 开放式文本生成3.4…...

解决由于找不到mfc140u.dll无法继续执行此代码问题的4个方法
mfc140u.dll是Microsoft Foundation Class(微软基础类库)中的一个动态链接库文件,它包含了许多用于实现Windows应用程序的基本功能。当我们在编写或运行基于MFC的程序时,如果系统中缺少这个文件,就会出现“找不到mfc14…...

MySQL高性能优化规范建议
当涉及到MySQL数据库的性能优化时,有许多方面需要考虑。以下是一些通用的MySQL性能优化规范建议: 合适的索引: 确保表中的字段使用了适当的索引。这能大幅提升检索速度。但避免过多索引,因为它会增加写操作的成本。 优化查询语句…...
pytorch 入门 (五)案例三:乳腺癌识别-VGG16实现
本文为🔗小白入门Pytorch内部限免文章 🍨 本文为🔗小白入门Pytorch中的学习记录博客🍦 参考文章:【小白入门Pytorch】乳腺癌识别🍖 原作者:K同学啊 在本案例中,我将带大家探索一下深…...

vue中electron与vue通信(fs.existsSync is not a function解决方案)
electron向vue发送消息 dist/main.js (整个文件配置在另一条博客里) win new BrowserWindow({width:1920,height:1080,webPreferences: {// 是否启用Node integrationnodeIntegration: true, // Electron 5.0.0 版本之后它将被默认false// 是否在独立 JavaScript 环境中运行…...

LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译
论文《LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks》翻译 LSTM-Based Anomaly Detection of Process Instances Benchmark and Tweaks翻译...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
