学习笔记|配对样本均数T检验|SPSS常用的快捷键|规范表达|《小白爱上SPSS》课程:SPSS第六讲 | 配对样本均数T检验
目录
- 学习目的
- 软件版本
- 原始文档
- 配对样本均数T检验
- 一、实战案例
- 二、案例解析
- 三、统计策略
- 四、SPSS操作
- 1、正态性检验
- 2、配对样本T检验
- 五、结果解读
- 六、规范报告
- 1、规范表格
- 2、规范文字
- 划重点
- Tips:SPSS常用的快捷键
学习目的
SPSS第六讲 | 配对样本均数T检验
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
配对样本均数T检验
配对样本均数T检验,指的是使受试对象在某一或者某些状况、特征因素上相同或者基本相同的试验设计。
上一讲的两独立样本T检验的两组数据是独立的,无关联的。而配对样本T检验中,两组样本数据是匹配的,存有关联的。
配对样本T检验常常用于实验性研究设计中,主要有三种方案。
两种同质受试对象分别接受两种不同的处理(异体配对)
同一受试对象接受两组不同的处理(自身平行配对)
同一对象处理前后的结果进行比较(自身前后配对)
一、实战案例
小白想研究长时间持续运动对血尿酸浓度(mg%)的影响,让10名大侠在自行车功力计上持续运动上两个小时(负荷为100W/min),问长时间持续运动对大侠的血尿酸浓度有无影响?
读取数据:
GET FILE='E:\*************\小白爱上SPSS\小白数据\第六讲 配对样本t 检验.sav'.

二、案例解析
看到两组数据,小白比较迷惑:到底是采用两独立样本T检验还是配对样本T检验?答案很简单,关键看两样本是独立还是关联。两独立样本均数T检验主要是两组【独立】样本比较,比如男生和女生的身高比较。而配对样本均数T检验的两组样本是有关联的。比如本案例是同一样本进行前后比较,个体的运动前和运动后的血尿酸浓度存有关联,属于自身前后配对。因此,初步判断,可采用配对样本均数的T检验。
三、统计策略
统计分析策略口诀“目的引导设计,变量确定方法”。
针对上述案例,扪心六问。
Q1:本案例研究目的是什么?
A:比较差异。比较运动干预前后两组的总体均数是否存有差异
Q2:比较的组数是多少呢?
A:两组数据,且这两组数据前后匹配
Q3:本案例属于什么研究设计?
A:实验性研究
Q4:有几个变量?
A:两个变量。其中,测试次序是分组变量,血尿酸浓度是结局变量
Q5:变量类型是什么?
A:一个分组(分类)变量,分成前测和后测两组;另一个连续型变量,血尿酸浓度
Q6:连续型变量服从正态分布么?
A:需要对前后测量的差值进行检验,而不是两组的正态性检验。若服从,采用配对样本T检验;若不服从正态,采用配对秩和检验。
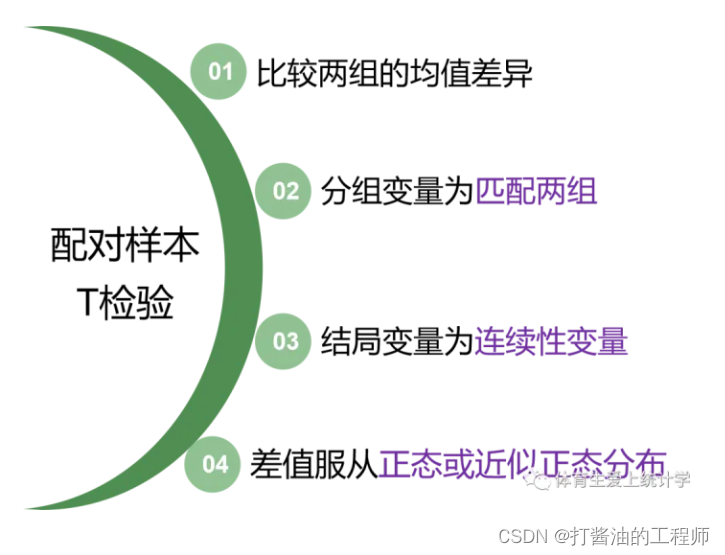
概括而言,如果数据满足以下条件,则采用配对样本T检验。
四、SPSS操作
1、正态性检验
配对样本T检验的主要检验两组差值数据是否服从正态分布,为此,首先要计算运动干预前减去干预后的血尿酸的差值。
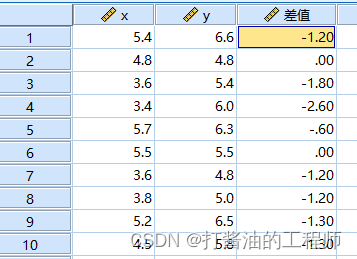
Step1:计算差值。
打开SPSS后,依次点击“转换”—“计算变量”,弹出对话框后,在目标变量中输入【差值】,在数据表达方式中,输入(x-y)【运动前-运动后】,注意:“运动前”和”运动后”可从类型和标签中放入。

点击确定后,在SPSS界面中就增加【差值】这一变量。
命令行:
COMPUTE 差值=x-y. /*计算差值(转换-计算变量)*/
EXECUTE /*执行*/.
Step2:对差值进行正态性检验
正态性检验的SPSS操作步骤请点击《第三讲 | 正态分布怎么检验?看这篇文章就够了》,这里只呈现检验结果。
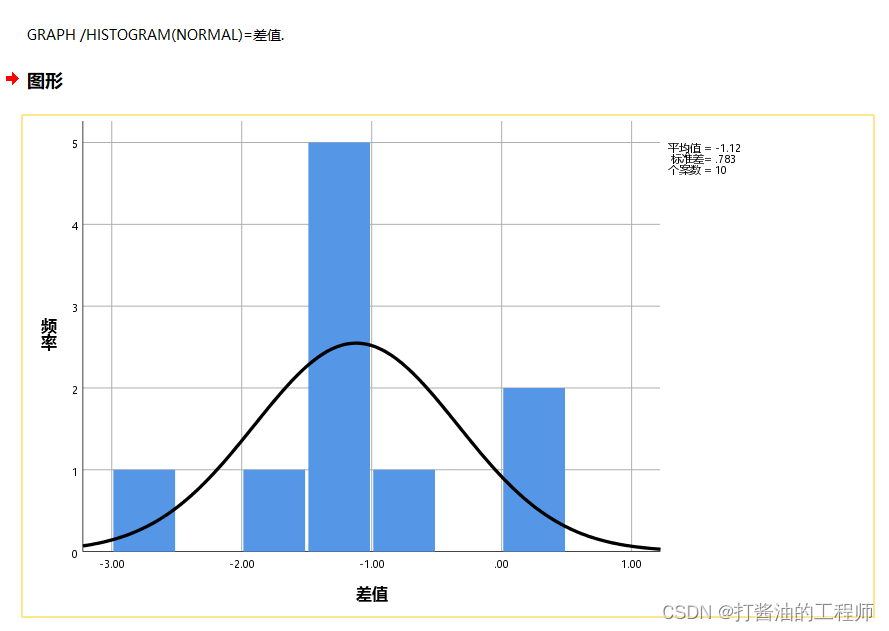
直方图绘制:
GRAPH /HISTOGRAM(NORMAL)=差值.
正态性检验:
EXAMINE VARIABLES=差值/PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.

本案例样本量≤50时,以夏皮洛-威尔克(S-W)检验为准,p=0.314>0.05,无统计学意义(接受原假设:数据按正态分布)。同时结合直方图,可认为差值数据服从正态性分布。
2、配对样本T检验
原始假设:两组数据无相关性。
Step1:打开SPSS,依次点击:分析→比较平均值→成对样本T检验
Step2:会出现配对数据框Variable1与Variable2,把【运动前】和【运动后】分别放进对应位置
Step3: 点击确定,就可呈现统计结果。
命令行:
T-TEST PAIRS=x WITH y (PAIRED) /CRITERIA=CI(.9500) /MISSING=ANALYSIS.
五、结果解读
配对t检验结果有3张表。
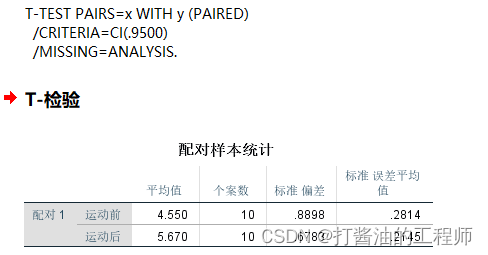
第1表:配对样本统计,运动前血尿酸浓度为4.55±0.89(mg%),运动后的浓度为5.67±0.68(mg%)。

第2表为两组数据相关性的统计学检验。本表不重要,它描述了配对数据的相关性程度和p值,本例相关性系数为0.529(该值范围从0-1,越大相关性越强,0.529属于具有一定的相关性,对原始假设存疑),P=0.116,表明它们相关系数没有达到显著性水平,其原因可能是样本量太少。事实上,受样本数量限制,在这里的P值没啥价值,关注相关系数即可。
第3表为配对t检验的结果,配对差值中的标准误差平均值为(.2814+.2415)/2=0.2476,(95%CI: -1.68,-0.56);检验统计量t=-4.524,p=0.001<0.05。配对差值与0值相比,差异具有统计学意义(不接受原始假设:两组数据无相关性)。
六、规范报告
规范报告有多种方式,本公众号只提供一种方式供参考。
1、规范表格
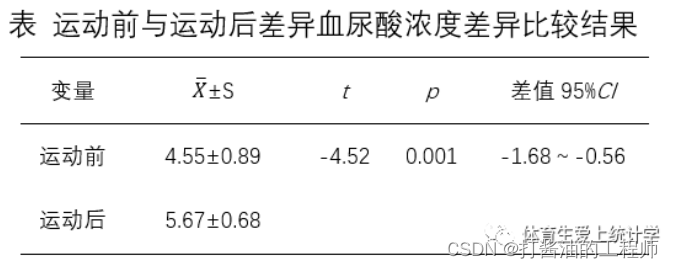
2、规范文字
由于数据服从正态分布,故采用配对样本均数的T检验。结果显示,长时间持续运动能显著提升血尿酸浓度t=-4.52,p=0.001,95%CI为(-1.68~-0.56)
小白将运动干预结果向主任报告,主任看后说:“看样子,给大侠们进行一次性运动干预还是有效果的,咱们就这么干,逐步扩大范围,让更多的组别参与干预”
小白心里嘀咕着 “更多组别,这怎么分析呀?”
主任看了小白一眼,“怎么啦,有难度吗?”
小白又一次挺直腰板说“没问题,不就是两两比较吗?”
主任向他诡异一笑,说“小白,你还是好好学习下一讲:单因素方差分析”
划重点
1、配对样本t检验来比较两个匹配样本的总体均数是否存有差异,一般用于实验性研究。
2、配对设计实验方案包括:异体配对、自身前后匹配、自身平行匹配。
3、配对样本t检验统计策略:分组变量为匹配两组、结局变量满足连续性、两组差值满足正态或近似正态分布。
Tips:SPSS常用的快捷键
引自:新手如何使用SPSS。
1.新建语法文件:Ctrl + N
2.打开数据文件:Ctrl + O
3.保存数据文件:Ctrl + S
4.关闭当前数据文件:Ctrl + F4
5.撤销上一步操作:Ctrl + Z
6.复制选中的内容:Ctrl + C
7.剪切选中的内容:Ctrl + X
8.粘贴内容:Ctrl + V
9.选择所有内容:Ctrl + A
10.运行选定项:Ctrl+R
11.关闭当前语法文件:Ctrl + F4
12.打开“数据编辑器”:Ctrl +1
13.打开“变量视图”:Ctrl +2
14.打开“输出视图”:Ctrl +3
15.打开“语法视图”:Ctrl +4
相关文章:

学习笔记|配对样本均数T检验|SPSS常用的快捷键|规范表达|《小白爱上SPSS》课程:SPSS第六讲 | 配对样本均数T检验
目录 学习目的软件版本原始文档配对样本均数T检验一、实战案例二、案例解析三、统计策略四、SPSS操作1、正态性检验2、配对样本T检验 五、结果解读六、规范报告1、规范表格2、规范文字 划重点Tips:SPSS常用的快捷键 学习目的 SPSS第六讲 | 配对样本均数T检验 软件版本 IBM S…...

python内置模块smtplib、email 发送电子邮件
一、简介 smtplib 是 Python 的标准库之一,用于发送电子邮件。它提供了一个简单的接口来连接到 SMTP(Simple Mail Transfer Protocol)服务器,并通过该服务器发送电子邮件。 email 是 Python 的标准库之一,用于处理电子…...

Qt使用QWebEngineView一些记录
1.关闭软件警告: Release of profile requested but WebEnginePage still not deleted. Expect troubles! 原因,系统退出关闭view,没有释放page。 解决办法:手动释放page 顺便把view也释放了。 Widget::~Widget() {updateIni…...

【2023.10.30练习】C语言-判断等式成立
计算机能力挑战初赛2020.20题 题目描述: 输入正整数A、B、C(0<A,B,C<10000),若用、-、*、/、%之一组成等式(即ABC,是上述运算符之一,),则输出“YES”,否则输出“NO”; 输入: 第一行输入…...
Wpf 使用 Prism 实战开发Day03
一.实现左侧菜单绑定 效果图: 1.首先需要在项目中创建 mvvm 的架构模式 创建 Models ,放置实体类。 实体类需要继承自Prism 框架的 BindableBase,目的是让实体类支持数据的动态变更! 例如: 系统导航菜单实体类 / <summary>/// 系统导航菜单实体类…...

JavaEE-cookie和session
本部分内容包括 cookie基本概念,sendcookies和getcookies代码; session基本概念,session实现登陆界面; 上述过程中涉及的代码如下: 1 import javax.servlet.ServletException; import javax.servlet.annotation.WebSe…...

Java设计模式之命令模式
目录 定义 结构 案例 优点 缺点 使用场景 JDK源码解析 Thread中start与run方法的区别 定义 将一个请求封装为一个对象,使发出请求的责任和执行请求的责任分割开。这样两者之间通过命令对象进行沟通,这样方便将命令对象进行存储、传递、调用、增…...

记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求 已知公式: t G A B F r B r 2 2 F A 2 B G A F ln ( r − A ) C o n s t t\frac{GAB}{F}r\frac{Br^2}{2F}\frac{A^2BGA}{F}\ln (r-A)Const tFGABr2FBr2FA2BGAln(r−A)Const 其中 t 的值为0-1000,每间隔25取一次值A2.12941E-10B0.…...

滑动窗口限流算法实现一
固定算法 原理:固定算法是将时间线分隔成固定大小的时间窗口,每个窗口都会有个计数器,用来记录窗口时间范围内的请求总数,如果窗口的请求总数达到最大限定值,会认定流量超限。比如将窗口大小设为1分钟,每分…...

简单明了!网关Gateway路由配置filters实现路径重写及对应正则表达式的解析
问题背景: 前端需要发送一个这样的请求,但出现404 首先解析请求的变化: http://www.51xuecheng.cn/api/checkcode/pic 1.请求先打在nginx,www.51xuecheng.cn/api/checkcode/pic部分匹配到了之后会转发给网关进行处理变成localho…...

EMQX内置Web管理控制台-Dashboard
一、Dashboard概述 EMQX Dashboard官网文档:https://docs.emqx.com/zh/enterprise/v5.1/dashboard/introduction.html 1、简介 EMQX 为用户提供了一个功能强大的内置管理控制台,即 EMQX Dashboard。通过这个控制台的 Web 界面,用户可以轻松监…...
计算机网络重点概念整理-第四章 网络层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言四、网络层4.1 网络层功能4.1.1 电路交换、报文交换与分组交换4.1…...

数组转树形数据
const nodes [{ id: 3, name: 节点C, pid: 1 },{ id: 6, name: 节点F, pid: 3 },{ id: 0, name: root, pid: null },{ id: 1, name: 节点A, pid: 0 },{ id: 8, name: 节点H, pid: 4 },{ id: 4, name: 节点D, pid: 1 },{ id: 2, name: 节点B, pid: 0 },{ id: 5, name: 节点E, p…...

react动态插入样式
在开发组件过程中,偶尔需要动态的插入css,比如在在iframe中渲染组件后,iframe中是没有样式的,所以需要手动插入样式。 插入样式 通常是在useLayoutEffect中动态创建style标签 useLayoutEffect(() > {if (!ref.current) {cons…...
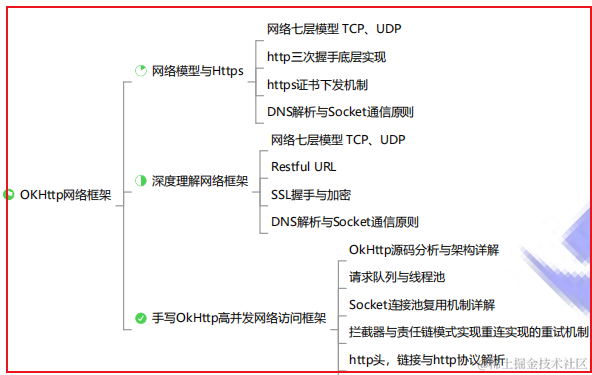
OkHttp网络框架深入理解-SSL握手与加密
OkHttp简介 由Square公司贡献的一个处理网络请求的开源项目,是目前Android使用最广泛的网络框架。从Android4.4开始HttpURLConnection的底层实现采用的是OkHttp。 特点: 支持HTTP/2并允许对同一主机的所有请求共享一个套接字通过连接池,减少了请求延迟…...
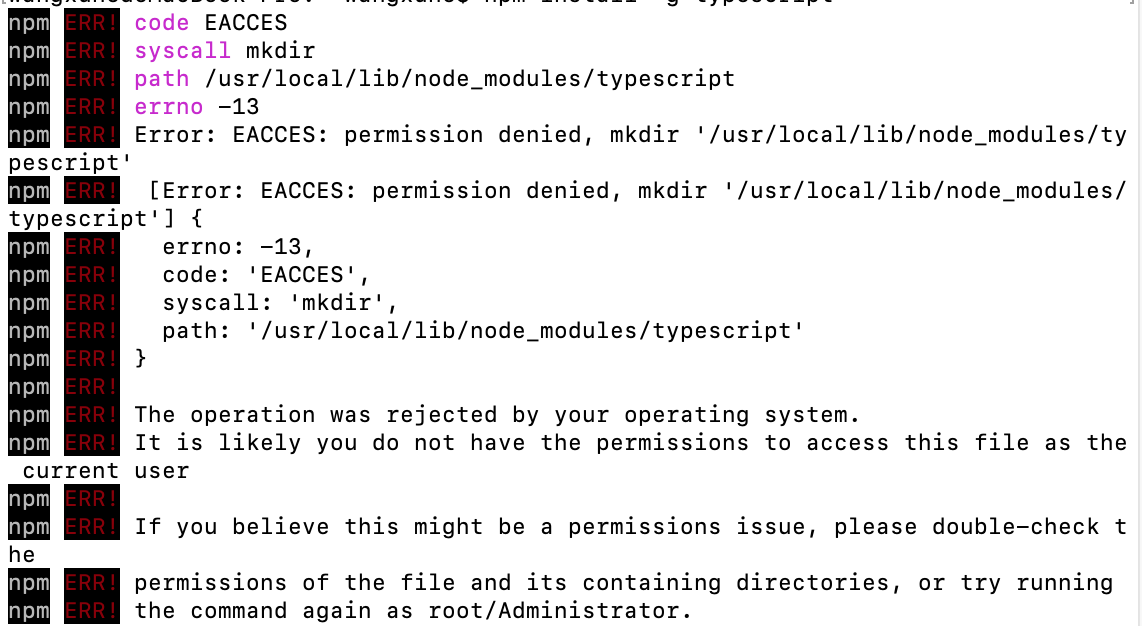
Mac 安装使用NPM及常用命令
环境: Mac 工具: NPM 可通过官网查询一些模块相关 NPM Doc 通过官网文档了解更多的关于NPM的使用 安装 NPM是Node.js的包管理工具,可用于解决 Node.js在代码部署上的问题。 新版本的Node.js已经集成了NPM, 因此可通过下载 Nod…...

利用 JSqlParser 防止 SQL 注入
高手文章《jsqlparser:实现基于SQL语法分析的SQL注入攻击检查》介绍了利用 JSqlParser 防止 SQL 注入,写得很好,只不过有两个问题,代码比较复杂,我于是作了简化,只有两个类;其次检测比较严格,连…...

10.27~10.29数电第三次实验分析与问题
实验要求 分析 寄存器 D触发器有两个输出口,一个输入口,一个时钟信号,一个复位信号 同步异步就是说复位信号在不在always里 给它加一个load就成了一位寄存器, 寄存器堆 8个8位的寄存器堆,每个寄存器都有两读一写…...
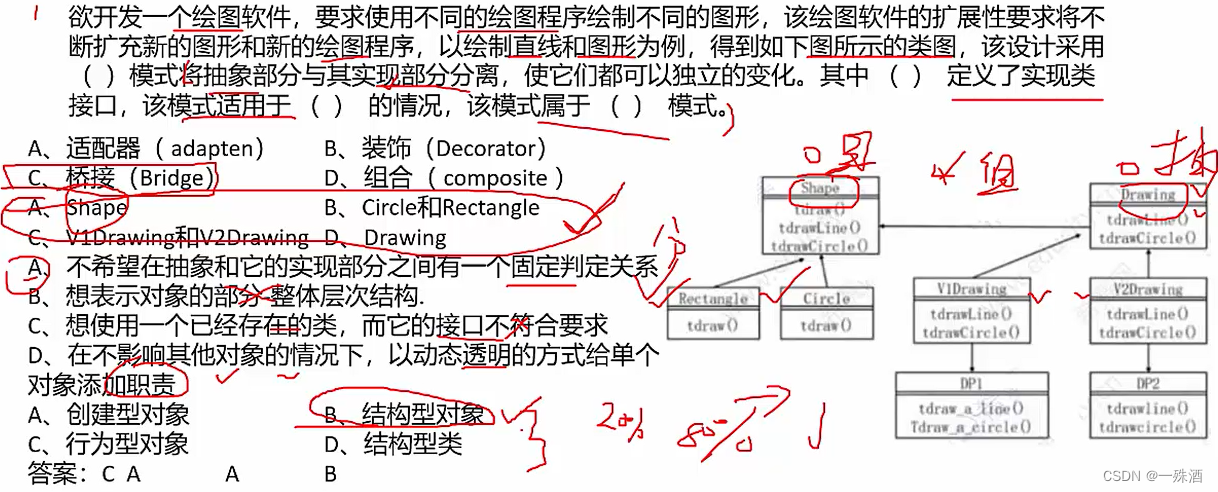
【软考】14.3 设计模式
《设计模式》 有下划线:类模式 / 对象模式无下划线:对象模式 创建型 设计模式 创建对象 构建器(Builder):类和构造分离抽象工厂(Abstract Factory):抽象接口工厂(Factor…...

Mac docker+vscode
mac 使用docker vs code 通过vscode 可以使用docker容器的环境。 可以在容器安装gdb, 直接调试代码。 创建容易时候可以指定目录和容易目录可以共享文件。...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
