Python稀疏矩阵最小二乘法
文章目录
- 最小二乘法
- 返回值
- 测试
最小二乘法
scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。
这两个函数可以求解Ax=bAx=bAx=b,或arg minx∥Ax−b∥2\argmin_x\Vert Ax-b\Vert^2argminx∥Ax−b∥2,或arg minx∥Ax−b∥2+d2∥x−x0∥2\argmin_x\Vert Ax-b\Vert^2+d^2\Vert x-x_0\Vert^2argminx∥Ax−b∥2+d2∥x−x0∥2,其中AAA必须是方阵或三角阵,可以有任意秩。
通过设置容忍度at,bta_t, b_tat,bt,可以控制算法精度,记r=b−Axr=b-Axr=b−Ax为残差向量,如果Ax=bAx=bAx=b是相容的,lsqr在∥r∥⩽at∗∥A∥⋅∥x∥+bt∥b∥\Vert r\Vert\leqslant a_t*\Vert A\Vert\cdot\Vert x\Vert + b_t\Vert b\Vert∥r∥⩽at∗∥A∥⋅∥x∥+bt∥b∥时终止;否则将在∥ATr∥⩽at∥A∥⋅∥r∥\Vert A^T r\Vert\leqslant a_t\Vert A\Vert \cdot\Vert r\Vert∥ATr∥⩽at∥A∥⋅∥r∥。
如果两个容忍度都是10−610^{-6}10−6,最终的∥r∥\Vert r\Vert∥r∥将有6位精度。
lsmr的参数如下
lsmr(A, b, damp=0.0, atol=1e-06, btol=1e-06, conlim=100000000.0, maxiter=None, show=False, x0=None)
参数解释:
A可谓稀疏矩阵、数组以及线性算子b为数组damp阻尼系数,默认为0atol,btol截止容忍度,是lsqr迭代的停止条件,即at,bta_t, b_tat,bt。conlim另一个截止条件,对于最小二乘问题,conlim应该小于10810^8108,如果Ax=bAx=bAx=b是相容的,则conlim最大可以设到101210^{12}1012iter_limint迭代次数show如果为True,则打印运算过程calc_var是否估计(A.T@A + damp**2*I)^{-1}的对角线x0阻尼系数相关
lsqr和lsmr相比,没有maxiter参数,但多了iter_lim, calc_va参数。
上述参数中,damp为阻尼系数,当其不为0时,记作δ\deltaδ,待解决的最小二乘问题变为
[AδI]x=[bδx0]\begin{bmatrix}A\\\delta I\end{bmatrix} x=\begin{bmatrix}b\\\delta x_0 \end{bmatrix} [AδI]x=[bδx0]
返回值
lsmr的返回值依次为:
x即Ax=bAx=bAx=b中的xxxistop程序结束运行的原因itn迭代次数normr∥b−Ax∥\Vert b-Ax\Vert∥b−Ax∥normar∥AT(b−Ax)∥\Vert A^T(b-Ax)\Vert∥AT(b−Ax)∥norma∥A∥\Vert A\Vert∥A∥condaA的条件数normx∥x∥\Vert x\Vert∥x∥
lsqr的返回值为
x即Ax=bAx=bAx=b中的xxxistop程序结束运行的原因itn迭代次数r1norm∥b−Ax∥\Vert b-Ax\Vert∥b−Ax∥r2norm∥b−Ax∥2+δ2∥x−x0∥2\sqrt{\Vert b-Ax\Vert^2+\delta^2\Vert x-x_0\Vert^2}∥b−Ax∥2+δ2∥x−x0∥2anorm估计的Frobenius范数Aˉ\bar AAˉacondAˉ\bar AAˉ的条件数arnorm∥ATr−δ2(x−x0)∥\Vert A^Tr-\delta^2(x-x_0)\Vert∥ATr−δ2(x−x0)∥xnorm∥x∥\Vert x\Vert∥x∥var(ATA)−1(A^TA)^{-1}(ATA)−1
二者的返回值较多,而且除了前四个之外,剩下的意义不同,调用时且须注意。
测试
下面对这两种算法进行验证,第一步就得先有一个稀疏矩阵
import numpy as np
from scipy.sparse import csr_arraynp.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)
然后用这个稀疏矩阵乘以一个xxx,得到bbb
xs = np.arange(500)
b = mat @ xs
接下来对这两个最小二乘函数进行测试
from scipy.sparse.linalg import lsmr, lsqr
import matplotlib.pyplot as plt
mx = lsmr(csr, b)[0]
qx = lsqr(csr, b)[0]
plt.plot(xs, lw=0.5)
plt.plot(mx, lw=0, marker='*', label="lsmr")
plt.plot(qx, lw=0, marker='.', label="lsqr")
plt.legend()
plt.show()
为了对比清晰,对图像进行放大,可以说二者不分胜负

接下来比较二者的效率,500×500500\times500500×500这个尺寸显然已经不合适了,用2000×20002000\times20002000×2000
from timeit import timeitnp.random.seed(42) # 设置随机数状态
mat = np.random.rand(500,500)
mat[mat<0.9] = 0
csr = csr_array(mat)
timeit(lambda : lsmr(csr, b), number=10)
timeit(lambda : lsqr(csr, b), number=10)
测试结果如下
>>> timeit(lambda : lsqr(csr, b), number=10)
0.5240591000001587
>>> timeit(lambda : lsmr(csr, b), number=10)
0.6156221000019286
看来lsmr并没有更快,看来斯坦福也不靠谱(滑稽)。
相关文章:

Python稀疏矩阵最小二乘法
文章目录最小二乘法返回值测试最小二乘法 scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。 这两个函数可以求解AxbAxbAxb,或arg minx∥Ax−b…...

mac本前端Homebrew下载,操作
1、打开电脑终端 2、下载Homebrew,在终端中输入 /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"开始下载Homebrew,因为这个地址是国外网站,下载失败的话,输入…...

Linux系统之查看进程监听端口方法
Linux系统之查看进程监听端口方法一、端口监听介绍二、使用netstat命令1.netstat命令介绍2.netstat帮助3.安装netstat工具4.列出所有监听 tcp 端口5.显示TCP端口的统计信息6.查看某个服务监听端口三、使用ss命令1.ss命令介绍2.ss命令帮助3.查看某个服务监听端口四、使用lsof命令…...
使用命令别名一键启动arthas
1. 使用命令别名启动arthas 确保单板上有jdk和arthas jdk目录:/home/xinliushijian/arthas/jdk arthas目录;/home/xinliushijian/arthas su xinliushijian编写脚本messi.sh cd /home/xinliushijian/arthas vi messi.sh 内容如下: #!/bin/ba…...

python+pytest接口自动化(2)-HTTP协议基础
HTTP协议简介HTTP 即 HyperText Transfer Protocol(超文本传输协议),是互联网上应用最为广泛的一种网络协议。所有的 WWW 文件都必须遵守这个标准。设计 HTTP 最初的目的是为了提供一种发布和接收 HTML 页面的方法。HTTP 协议在 OSI 模型中属…...

操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 注:阅读本编文章前,请先阅读系列文章,以…...
非常好看的html网页个人简历
一. 前言 文末获取gitee链接 在前几天逛b站的时候,发现了个比较实用的东西-----个人简介网页版,相当于网页版的个人简历,相较于PDF形式的,网页版所能呈现内容更加丰富,而且更加美观,在BOOS上被HR小姐姐要…...
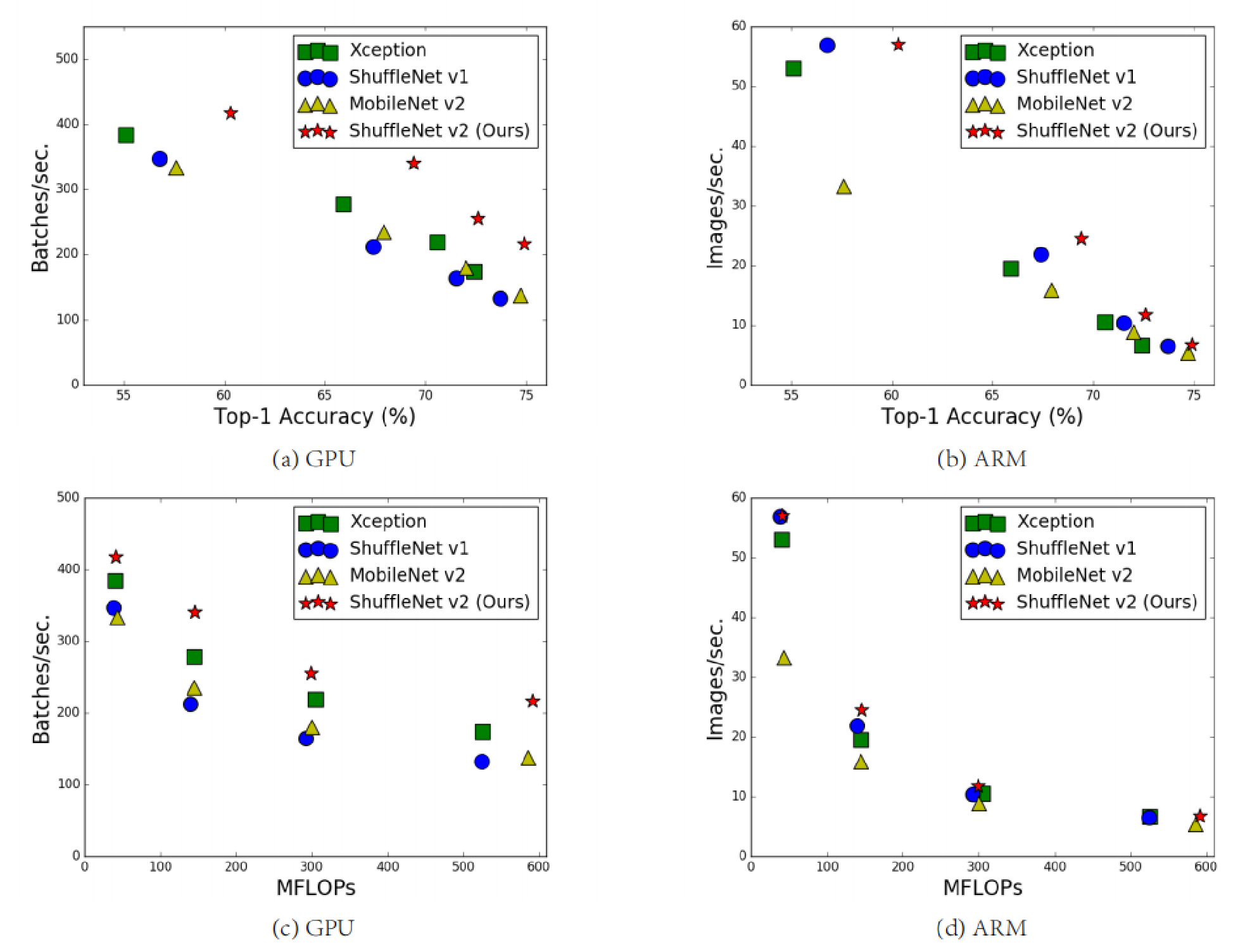
轻量级网络模型ShuffleNet V2
在学习ShuffleNet V2内容前需要简单了解卷积神经网络和MobileNet,以及Shuffnet V1的相关内容,大家可以出门左转,去看我之前的几篇博客MobileNet发展脉络(V1-V2-V3),轻量级网络模型ShuffleNet V1🆗ÿ…...
分享美容美发会员管理系统功能的特点_美容美发会员管理系统怎么做
人们越来越关心美发,美发行业发展迅速,小程序可以连接在线场景,许多美发院也开发了会员卡管理系统。那么一个实用的美发会员管理系统怎么制作呢?它有什么功能?我们一起来看看~(干货满满,耐心看完…...

Oracle-05-DCL篇
🏆一、简介 Oracle的DCL代表数据库控制语言,用于管理数据库对象的访问和安全性。DCL的两个主要命令是GRANT和REVOKE。 GRANT命令用于授予用户或角色对数据库对象的访问权限,例如表、视图或存储过程。GRANT命令的语法如下: GRANT privilege_name [, privilege_name]... …...

tess4j简单使用入门
tess4j下载 下载地址: https://sourceforge.net/projects/tess4j/ 不要直接下载,点击files,然后下载最新版 下载解压后放到指定的目录即可,这里放到d:\jar目录下 tess4j根目录: d:\jar\tess4j tess4j使用 把test4j项目目录中dist和lib目录下的所有jar包导入到需要的项目中…...

WebGPU学习(4)---使用 UniformBuffer
接下来让我们使用 UniformBuffer。UniformBuffer 是一个只读内存区域,可以在着色器上访问。 这次,我们将传递给着色器的矩阵存储在 UniformBuffer 中。演示示例 1.在顶点着色器中的 UniformBuffer 这次我们在顶点着色器里定义一个名为Uniforms的新结构体…...

Http客户端Feign-远程调用
Feign的使用步骤 引入依赖添加EnableFeignClients注解编写FeignClient接口使用FeignClient中定义的方法代替RestTemplate Feign的日志配置 1.方式一是配置文件,feign.client.config.xxx.loggerLevel 如果xxx是default则代表全局如果xxx是服务名称,例如userservi…...

RK3568镜像的拆包和打包
文章目录 前言一、window上分包和打包分包打包二、Linux上分包和打包分包打包总结前言 本文记录在win10上利用瑞芯微提供的工具进行分包和打包,同样也有Linux教程 提示:以下是本篇文章正文内容,下面案例可供参考 一、window上分包和打包 分包 window下一般直接利用工具即…...

《设计模式》适配器模式
《设计模式》适配器模式 适配器(Adapter)是一种结构型设计模式,它允许我们将一个类的接口转换成另一个类的接口,从而使得原本由于接口不兼容而无法合作的类能够一起工作。适配器模式通常用于以下情况: 在已有的类中添…...

linux 随笔 5-服务管理
0. 装到虚拟机与物理机,感觉各有各的不方便 Linux下systemctl命令和service、chkconfig命令的区别 1. service 根据/etc/init.d目录下的配置,做服务相关的: 启动停止重新启动关闭系统服务 2. chkconfig 用于维护 /etc/rc[0-6].d 的命令…...
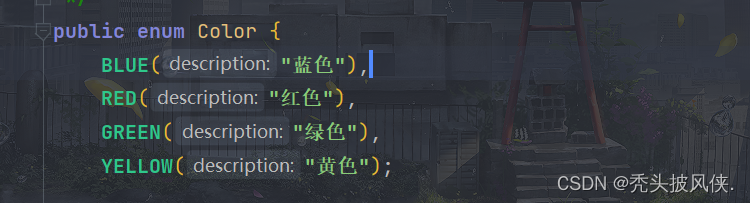
【java基础】枚举类(enum)
文章目录基本介绍快速使用字段、方法、构造器枚举类方法toString方法valueOf方法values方法ordinal方法基本介绍 在java中有一种特殊的类型就是枚举类,对于一个有限的有固定值的集合,我们就可以考虑使用枚举类来进行表示,例如服装的大小为 小…...

Linux2
(1)root用户的主目录: (3)查看 (4)远程登陆系统:CentOS7上使用ifconfig查看IP,使用putty远程登陆 (5)查询目前用户登录情况:who命令…...

C语言基础应用(二)数据的转换与输入输出
学习了C语言的基本数据类型后,我们可能会想这些数据如何进行运算,是否可以让不同类型的数据直接进行运算呢? 一、数据类型转换 1.1 int类型与float类型之间的转换 int i 5; // j值为2.000000 因为左右操作数均为整型float j i/2; // …...
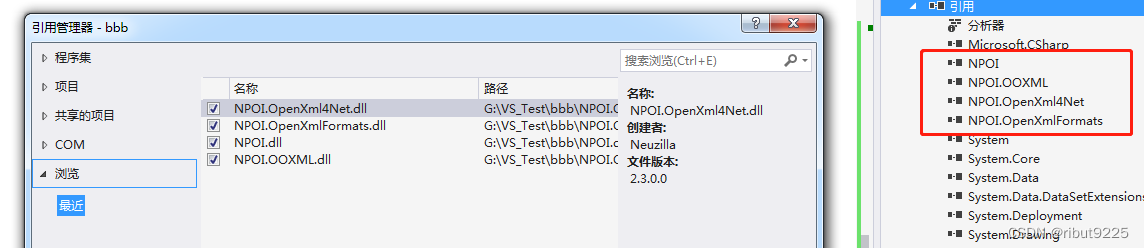
C# 用NPOI读取EXCEL
1. 复制DLL文件 ICSharpCode.SharpZipLib.dll NPOI.dll NPOI.OOXML.dll NPOI.OpenXml4Net.dll NPOI.OpenXmlFormats.dll 2. 在工程中添加引用 3. using System.IO; using NPOI.HSSF.UserModel; using NPOI.XSSF.UserModel; using NPOI.SS.UserModel; using NPOI.OpenXml4Ne…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...
