Leetcode100-两数之和
参见官方题解
一、学到的知识
-
正面寻找两个数之和相加等于某个数,如 a+b = c,不如反过来寻找 a = c - b
正面寻找需要两层 for 循环,把每个数都进行遍历,所以时间复杂度较高
反过来则可以通过维护一个 a 的集合,每次通过查询 c - b 是否在集合中,判断是否存在 a = c - b
存在,则返回答案;不存在,则将 a 插入集合中, 待下次查询
-
想一下,我们为什么把 a 插入集合中,而不是 c - b呢?
如果把 c - b 插入集合,意味着我们将判断 a 是否在集合中,总之就是要判断是否存在 a = c - b,两者写法其实都可以
二、代码
-
版本1
时间复杂度 O(N)
空间复杂度 O(1)比较好想到的一个方法是先使用一层 for 循环枚举 a,再使用一层 for 循环枚举 b,判断 a + b == c 是否为真即可
而且也容易想到一点优化,对于位于 x 位置的元素,1…x-1次循环的时候,nums[x]已经被匹配过,所以无需再匹配,所以在代码中,可以看到,第二层枚举 b 的循环,从 i + 1 开始class Solution { public:vector<int> twoSum(vector<int>& nums, int target){const int Size = nums.size();for (int i = 0; i < Size; ++i){for (int j = i + 1; j < Size; ++j){if (nums[i] + nums[j] == target){return {i, j};}}}return {0, 0};} }; -
版本2
时间复杂度 O(NlogN)
空间复杂度 O(N)这是版本1的优化, 前文提过,需要寻找 a + b = c,我们可以把 b 移至右侧,寻找 a = c - b,我们很自然的想到,可以维护一个数的集合,再从中寻找元素是否存在
而这个集合的查找的复杂度,就决定了我们算法的复杂度,在代码中,我们使用了标准库中的 map,它的查找效率是 LogN
class Solution { public:std::vector<int> twoSum(std::vector<int>& nums, int target){const int size = nums.size();map<int, int> Map;for (int i = 0; i < size; ++i){const int gap = target - nums[i];auto iterator = Map.find(gap);if (iterator != Map.end()){return {iterator->second, i};}Map.insert({nums[i], i});}return {-1, -1};} };
相关文章:

Leetcode100-两数之和
参见官方题解 一、学到的知识 正面寻找两个数之和相加等于某个数,如 ab c,不如反过来寻找 a c - b 正面寻找需要两层 for 循环,把每个数都进行遍历,所以时间复杂度较高 反过来则可以通过维护一个 a 的集合,每次通过…...

4565: 删除中间的*
描述规定输入的字符串中只包含字母和*号,除了字符串前导和尾部的*号之外,将串中其他*号全部删除输入输入数据包括一串字符串,只包含字母和*,总长度不超过80。输出输出删除中间*后的字符串。样例输入*******A*BC*DEF*G****样例输出*******ABCD…...

VUE组件示例说明
<!-- * Author: xxx.xx * Date: 2021-07-20 14:33:41 * LastEditors: xxx.xx * LastEditTime: 2021-07-20 18:22:37 * PageTitle: 上拉加载组件 * Description: 描述... * FilePath: /wxapp-view/components/loadmore.vue --> <template><view class"c-mor…...
Widget中的State-学习笔记
Widget 有 StatelessWidget 和 StatefulWidget 两种类型。StatefulWidget 应对有交互、需要动态变化视觉效果的场景,而 StatelessWidget 则用于处理静态的、无状态的视图展示。StatefulWidget 的场景已经完全覆盖了 StatelessWidget,因此我们在构建界面时…...
)
股市实战技巧(知行合一)
投资策略 长线:优质核心股票大仓位核心标的票,小仓位短线投资投机小储蓄可加大投机仓位价值投资也要去做仓位控制 行情好,总体大仓位,行情小,小仓位个股根据走势调整个股仓位(布林线的20%原则)…...

k8s-资源限制-探针检查
文章目录一、资源限制1、资源限制的使用2、reuqest资源(请求)和limit资源(约束)3、Pod和容器的资源请求和限制4、官方文档示例5、资源限制实操5.1 编写yaml资源配置清单5.2 释放内存(node节点,以node01为例…...

一文让你彻底了解Linux内核文件系统
一,文件系统特点 文件系统要有严格的组织形式,使得文件能够以块为单位进行存储。文件系统中也要有索引区,用来方便查找一个文件分成的多个块都存放在了什么位置。如果文件系统中有的文件是热点文件,近期经常被读取和写入…...

解决前端组件下拉框选择功能失效问题
问题: 页面下拉框选择功能失效 现象: 在下拉框有默认值的情况下,点击下拉框的其他值,发现并没有切换到其他值 但是在下拉框没默认值的情况下,功能就正常 原因 select 已经绑定选项(有默认值) 在…...

Linux_vim编辑器入门级详细教程
前言(1)vim编辑器其实本质上就是对文本进行编辑,比如在.c文件中改写程序,在.txt文件写笔记什么的。一般来说,我们可以在windows上对文本进行编译,然后上传给Linux。但是有时候我们可能只是对文本进行简单的…...

TCP 的演化史-TCP 是一个过渡
TCP 诞生于 1970 年代早期,彼时没有分组交换网的大规模应用,彼时绝大多数通信都在使用电话,电报,电挂等电路交换技术。 诞生在这种环境下的技术不可能脱离时代的影响,如果一个孩子出生在一个父母关系冷漠的家庭&#x…...

Flask
Flask第三方组件非常全,适合小型 API服务类项目,但第三方组件运行稳定性相对Django差。 基础知识 Flask安装 pip install flask2.0.3Flask库文件 Jinjia2:模板渲染库Markupsafe:返回安全标签 只要Flask返回模板或者标签时都会…...

SAP系统与MES系统的数据协同技术方案
1.MES介绍 本文中提到的MES系统是在西门子公司的SIMATIC IT平台上开发完成。所有的应用子系统进行统一分析、统一设计、统一开发,利用统一的开发平台和数据库系统,保证了管理系统的集成性、高效性。 2.数据协同接口包含的…...
2018年蓝桥杯省赛试题-5道(Python)
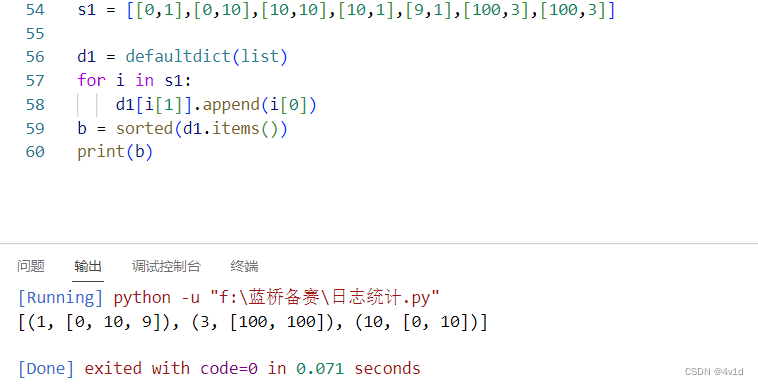
文章目录一、日志统计思考二、递增三元组思考三、螺旋折线思考四、乘积最大思考五、全球变暖思考尾声提示:以下是本篇文章正文内容,下面案例可供参考 一、日志统计 题目描述 小明维护着一个程序员论坛。 现在他收集了一份"点赞"日志…...

Python稀疏矩阵最小二乘法
文章目录最小二乘法返回值测试最小二乘法 scipy.sparse.linalg实现了两种稀疏矩阵最小二乘法lsqr和lsmr,前者是经典算法,后者来自斯坦福优化实验室,据称可以比lsqr更快收敛。 这两个函数可以求解AxbAxbAxb,或arg minx∥Ax−b…...

mac本前端Homebrew下载,操作
1、打开电脑终端 2、下载Homebrew,在终端中输入 /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"开始下载Homebrew,因为这个地址是国外网站,下载失败的话,输入…...

Linux系统之查看进程监听端口方法
Linux系统之查看进程监听端口方法一、端口监听介绍二、使用netstat命令1.netstat命令介绍2.netstat帮助3.安装netstat工具4.列出所有监听 tcp 端口5.显示TCP端口的统计信息6.查看某个服务监听端口三、使用ss命令1.ss命令介绍2.ss命令帮助3.查看某个服务监听端口四、使用lsof命令…...
使用命令别名一键启动arthas
1. 使用命令别名启动arthas 确保单板上有jdk和arthas jdk目录:/home/xinliushijian/arthas/jdk arthas目录;/home/xinliushijian/arthas su xinliushijian编写脚本messi.sh cd /home/xinliushijian/arthas vi messi.sh 内容如下: #!/bin/ba…...

python+pytest接口自动化(2)-HTTP协议基础
HTTP协议简介HTTP 即 HyperText Transfer Protocol(超文本传输协议),是互联网上应用最为广泛的一种网络协议。所有的 WWW 文件都必须遵守这个标准。设计 HTTP 最初的目的是为了提供一种发布和接收 HTML 页面的方法。HTTP 协议在 OSI 模型中属…...

操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 注:阅读本编文章前,请先阅读系列文章,以…...
非常好看的html网页个人简历
一. 前言 文末获取gitee链接 在前几天逛b站的时候,发现了个比较实用的东西-----个人简介网页版,相当于网页版的个人简历,相较于PDF形式的,网页版所能呈现内容更加丰富,而且更加美观,在BOOS上被HR小姐姐要…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
