GPS学习(一):在ROS2中将GPS经纬度数据转换为机器人ENU坐标系,在RVIZ中显示坐标轨迹
文章目录
- 一、GPS模块介绍
- 二、坐标转换
- 转换原理
- 参数解释:
- 增加回调函数
- 效果演示
本文记录在Ubuntu22.04-Humbel中使用NMEA协议GPS模块的过程,使用国产ROS开发板鲁班猫(LubanCat )进行调试。
一、GPS模块介绍
在淘宝找了款性价比较高的轮趣科技GPS北斗双模定位模块作为入门学习使用,支持GNSS系统(北斗、GPS、GLONASS、日本的QZSS以及卫星增强系统SBAS),定位精度在2.5m左右,属于民用级别。引出了常用的几个外部接口,主要用type-c调试比较方便,售后技术也相当给力。接线示意图如下,注意:测试时需要将GPS天线放置在室外,否则模块将没有GPS信号

二、坐标转换
机器人基于Ubuntu-ROS平台做开发调试,所以需要将GPS模块的经纬度和高度信息转化为机器人所能认识的本地坐标系(局部笛卡尔坐标系)。参考其他博主案例,使用半正矢公式来将经纬度转为xyz坐标值。
转换原理
半正矢公式介绍:
半正矢公式是一种根据两点的经度和纬度来确定大圆上两点之间距离的计算方法,在导航有着重要地位。它是球面三角学中“半正矢定理”公式的特例,该定理涉及了球面三角形的边和角。
对于任何球面上的两点,圆心角的半正矢值可以通过如下公式计算:
hav( d r \frac{d}{r} rd)=hav( ψ 2 \psi_{2} ψ2- ψ 1 \psi_{1} ψ1)+cos( ψ 1 \psi_{1} ψ1)cos( ψ 2 \psi_{2} ψ2)hav( λ 2 \lambda_{2} λ2- λ 1 \lambda_{1} λ1)
hav 是半正矢函数的缩写:
haversin( θ \theta θ)= s i n 2 sin^{2} sin2( ( θ ) 2 \frac{(\theta)}{2} 2(θ))= 1 − c o s ( θ ) 2 \frac{1-cos(\theta)}{2} 21−cos(θ)
参数解释:
d :两点之间的距离(沿大圆,见球面距离);
r :球的半径;
ψ 1 \psi_{1} ψ1 ψ 2 \psi_{2} ψ2 :点 1 的纬度和点 2 的纬度,以弧度制度量;
λ 1 \lambda_{1} λ1 λ 2 \lambda_{2} λ2:点 1 的经度和点 2 的经度,以弧度制度量。
等号左边的 d r \frac{d}{r} rd:圆心角,单位是弧度。
所以,可以通过应用反半正矢函数(如果可以查到值)或通过使用反正弦函数来解出d :
d = r ∗ a r c h a v ( h ) d=\sqrt[]{r*archav(h)} d=r∗archav(h) = 2r*arcsin h \sqrt[]{h} h)
将h=hav d r \frac{d}{r} rd代入后可得:

对于中短距离来说,半正矢公式是计算地球表面 GPS 坐标之间距离的有用且相对准确的方法,在距离较长时其准确性可能会降低。
增加回调函数
这里简单解释一下gpsCallback回调函数的内容,此处订阅sensor_msgs::msg::NavSatFix数据格式的GPS话题进行数据处理。
//将纬度和经度值从度数转换为弧度。
double rad(double d)
{return d * 3.1415926 / 180.0;
}
void gps_callback(const sensor_msgs::msg::NavSatFix::SharedPtr gps_msg)
{if (!pose_init){// Initialization code remains the same.//使用接收到的 GPS 消息中的纬度、经度和高度false进行初始化,只初始化一次init_pose.latitude = gps_msg->latitude;init_pose.longitude = gps_msg->longitude;init_pose.altitude = gps_msg->altitude;init = true;}else{//计算当前 GPS 位置与初始 GPS 位置之间的纬度和经度变化double radLat1 ,radLat2, radLong1,radLong2,delta_lat,delta_long,x,y;double deltaLat_y ,deltaLong_x;deltaLat_x = 0; deltaLong_y = 0;radLat1 = rad(init_pose.latitude);//初始化位置的纬度radLong1 = rad(init_pose.longitude);//初始化位置的经度radLat2 = rad(gps_msg->latitude);//当前位置的纬度radLong2 = rad(gps_msg->longitude);//当前位置的经度deltaLat = radLat2 - radLat1; deltaLong = radLong2 - radLong1;// 代入公式进行计算x的坐标值x = 2 * asin(sqrt(pow(sin(delta_lat / 2), 2) + cos(radLat1) * cos(radLat2) * pow(sin(deltaLong_y / 2), 2));//公式计算结果默认为弧度,所以这里要转换成m的单位x = x * EARTH_RADIUS * 1000; // 代入公式进行计算y的坐标值y = 2 * asin(sqrt(pow(sin(deltaLat_x / 2), 2) + cos(radLat2) * cos(radLat2) * pow(sin(deltaLong / 2), 2));y = y * EARTH_RADIUS * 1000; // Convert to meters.// 将高度差计算为z的坐标值double z = gps_msg->altitude - init_pose.altitude;//将计算得到的xyz值发布为ROS中的PoseStamped数据,作为路径发布ros_path_.header.frame_id = "path";ros_path_.header.stamp = rclcpp::Node::now();geometry_msgs::msg::PoseStamped pose;pose.header = ros_path_.header;pose.pose.position.x = x;pose.pose.position.y = y;pose.pose.position.z = z;ros_path_.poses.push_back(pose);state_pub_.publish(ros_path_);}
}效果演示
使用nmea_navsat_driver驱动启动GPS模块,源码链接:https://github.com/ros-drivers/nmea_navsat_driver/tree/ros2
ros2 launch nmea_navsat_driver nmea_serial_driver.launch.py
然后启动坐标转换节点,将经纬度数据从WGS-84 坐标转换到机器人真实世
界 xyz 坐标系下(一般为东北天方向),以第一个经纬度数据为原点,不断描绘实时经纬度数据的位移方向,显示为机器人运行轨迹图。
ros2 launch gps_path gps_path.launch.py
打开rviz2,修改 Fixed Frame 为path,电机左下角[add],根据topic添加[gps_path]->path后,显示效果为:

相关文章:

GPS学习(一):在ROS2中将GPS经纬度数据转换为机器人ENU坐标系,在RVIZ中显示坐标轨迹
文章目录 一、GPS模块介绍二、坐标转换转换原理参数解释: 增加回调函数效果演示 本文记录在Ubuntu22.04-Humbel中使用NMEA协议GPS模块的过程,使用国产ROS开发板鲁班猫(LubanCat )进行调试。 一、GPS模块介绍 在淘宝找了款性价比较高的轮趣科技GPS北斗双…...

chatgpt生成文本的底层工作原理是什么?
文章目录 🌟 ChatGPT生成文本的底层工作原理🍊 一、数据预处理🍊 二、模型结构🍊 三、模型训练🍊 四、文本生成🍊 总结 📕我是廖志伟,一名Java开发工程师、Java领域优质创作者、CSDN…...

javaEE -11(10000字HTML入门级教程)
一: HTML HTML 代码是由 “标签” 构成的. 例如: <body>hello</body>标签名 (body) 放到 < > 中大部分标签成对出现. 为开始标签, 为结束标签.少数标签只有开始标签, 称为 “单标签”.开始标签和结束标签之间, 写的是标签的内容. (h…...

LeetCode75——Day21
文章目录 一、题目二、题解 一、题目 1207. Unique Number of Occurrences Given an array of integers arr, return true if the number of occurrences of each value in the array is unique or false otherwise. Example 1: Input: arr [1,2,2,1,1,3] Output: true Ex…...

学习笔记---更进一步的双向链表专题~~
目录 1. 双向链表的结构🦊 2. 实现双向链表🐝 2.1 要实现的目标🎯 2.2 创建初始化🦋 2.2.1 List.h 2.2.2 List.c 2.2.3 test.c 2.2.4 代码测试运行 2.3 尾插打印头插🪼 思路分析 2.3.1 List.h 2.3.2 List.…...

vscode格式化代码, 谷歌风格, 允许短if同行短块同行, tab = 4舒适风格
ctrl ,输入format, 点开C风格设置 在这块内容输入{ BasedOnStyle: Chromium, IndentWidth: 4, ColumnLimit: 200, AllowShortIfStatementsOnASingleLine: true, AllowShortLoopsOnASingleLine: true} C_Cpp: Clang_format_fallback Style 用作回退的预定义样式的名称&#x…...
百度富文本上传图片后样式崩塌
🔥博客主页: 破浪前进 🔖系列专栏: Vue、React、PHP ❤️感谢大家点赞👍收藏⭐评论✍️ 问题描述:上传图片后,图片会变得很大,当点击的时候更是会顶开整个的容器的高跟宽 原因&#…...

autoware.ai中检测模块lidar_detector caffe
lidar_apollo_cnn_seg_detect模块:该模块主要是调用百度apollo的目标分割。 1.需要安装caffe进行实现: caffe安装步骤: git clone https://github.com/BVLC/caffecd caffe && mdkir build && cd buildcmake ..出现报错: CM…...

CentOS安装Ruby环境
安装依赖项 sudo yum install -y perl zlib-devel openssl-devel安装git sudo yum install -y git git config --global http.sslVerify falsecurl取消ssl认证 echo "insecure" >> ~/.curlrc安装rbenv https://github.com/rbenv/rbenv git clone https://…...
 c++)
力扣第509题 斐波那契数 新手动态规划(推荐参考) c++
题目 509. 斐波那契数 简单 相关标签 递归 记忆化搜索 数学 动态规划 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0&a…...

canvas绘制签名并保存
实现签名的三个关键方法: 1.mousedown:当鼠标按下时开始绘制签名。 2.mousemove:鼠标移动时持续绘制。 3.mouseup:鼠标抬起时结束绘制。 html: <div class"setSign"><canvasref"canvas&q…...
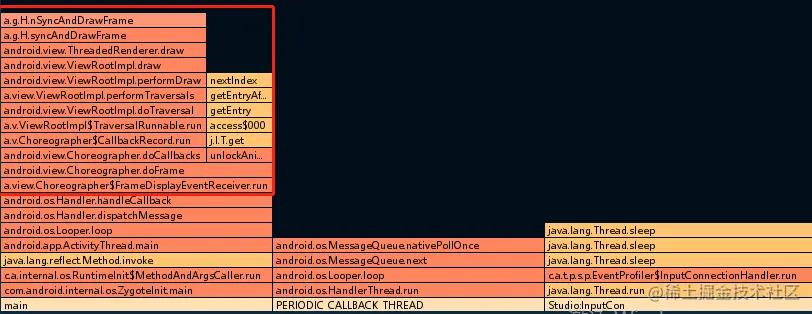
Android渲染流程
目录 缓冲区的不同生命周期代表当前缓冲区的状态: 多个源 ViewRootImpl: Android4.0: Android5.0: Android应用程序调用SurfaceFliger将测量,布局,绘制好的Surface借助GPU渲染显示到屏幕上。 一个Acti…...

牛客-【237题】算法基础精选题单-第二章 递归、分治
第二章 递归、分治 递归NC15173 The Biggest Water ProblemNC22164 更相减损术 递归 NC15173 The Biggest Water Problem 简单递归,直接暴力 #include <math.h> #include <stdio.h> #include <algorithm> #include <cstring> #include &…...

leetcode-字符串
1.反转字符串LeetCode344. 20230911 难度为0,此处就不放代码了 注意reverse和swap等一系列字符串函数什么时候该用,记一记库函数 swap可以有两种实现,涨知识了,除了temp存值还可以通过位运算:s[i] ^ s[j]; s[j] ^ s[i…...

多线程---synchronized特性+原理
文章目录 synchronized特性synchronized原理锁升级/锁膨胀锁消除锁粗化 synchronized特性 互斥 当某个线程执行到某个对象的synchronized中时,其他线程如果也执行到同一个对象的synchronized就会阻塞等待。 进入synchronized修饰的代码块相当于加锁 退出synchronize…...
Qt实现卡牌对对碰游戏
效果 闲来无事,实现一个对对碰游戏,卡牌样式是火影动漫。 先上效果: 卡牌对对碰_火影主题 玩法 启动游戏,进入第一关卡,所有卡牌都为未翻开状态,即背面朝上;点击卡牌,则将卡牌翻开…...

【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割7(数据预处理)
在上一节:【3D 图像分割】基于 Pytorch 的 VNet 3D 图像分割6(数据预处理) 中,我们已经得到了与mhd图像同seriesUID名称的mask nrrd数据文件了,可以说是一一对应了。 并且,mask的文件,还根据结…...

极米科技H6 Pro 4K、H6 4K高亮定焦版——开启家用投影4K普及时代
智能投影产业经过几年发展,市场规模正在快速扩大。洛图数据显示,预计今年中国投影出货量有望超700万台,2027年达950万台,可见智能投影产业规模将逐渐壮大,未来可期。2023年,投影行业呈现出全新面貌…...
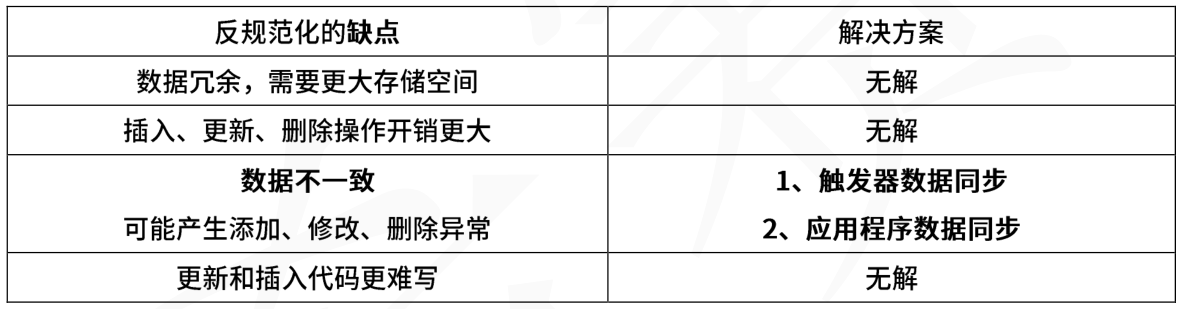
软考系统架构师知识点集锦九:数据库系统
一、考情分析 二、考点精讲 2.1数据库概述 2.1.1数据库模式 (1)三级模式:外模式对应视图,模式(也称为概念模式)对应数据库表,内模式对应物理文件。(2)两层映像:外模式-模式映像,模式-内模式映像;两层映像可以保证数据库中的数据具有较高的…...

IOC课程整理-6 Spring IoC 依赖注入
1 依赖注入的模式和类型 模式 类型 2 自动绑定(Autowiring) 官方定义 “自动装配是Spring框架中一种机制,用于自动解析和满足bean之间的依赖关系。通过自动装配,Spring容器可以根据类型、名称或其他属性来自动连接协作的bean&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
