Leetcode 542. 01 矩阵
542. 01 矩阵-中等
问题描述
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
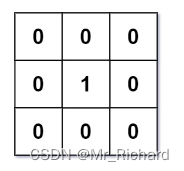
输入:mat = [[0,0,0],[0,1,0],[0,0,0]]
输出:[[0,0,0],[0,1,0],[0,0,0]]
示例 2:
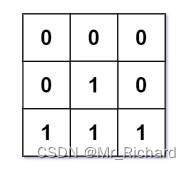
输入:mat = [[0,0,0],[0,1,0],[1,1,1]]
输出:[[0,0,0],[0,1,0],[1,2,1]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.mat中至少有一个0
解题思路与代码实现一
采用BFS搜索解题:
- 创建标记数组visited用于标记已访问过的元素,初始化均为Integer.MAX_VALUE(不小于可能的最大步长m+n-1),因为在BFS的过程中,先被访问的元素的步长一定小于等于后被访问的元素;创建队列queue用于实现BFS,初始化均为false;
- 扫描mat数组,需要把所有
mat[i][j]为0的元素加入队列并标记为已访问; - 接着扫描队列,当队列不为空时,队头元素出队,依次访问其上下左右的周围点,如果未发生数组越界且该周围点没被访问过,则将其入队并标记为已访问(true),同时更新周围点的步长 = 出队元素的步长 +1;
public int[][] updateMatrix2(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// 依次表示 上、左、下、右周围四个点的偏移量int[][] dirs = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}};// BFS用的队列Queue<int[]> queue = new LinkedList<>();// 标记数组boolean[][] visited = new boolean[m][n];for (int i = 0; i < m; i++) {// 标记数组初始化全为false,mat[i][j]为0的元素会被标记为trueArrays.fill(visited[i], false);for (int j = 0; j < n; j++) {if (mat[i][j] == 0) {// mat[j][j]为0的元素标记为true并优先入队visited[i][j] = true;queue.offer(new int[]{i, j});} else {mat[i][j] = Integer.MAX_VALUE;}}}while (!queue.isEmpty()) {// 从队列中取出访问过的一个元素作为当前点,访问其周围点int[] current = queue.poll();int currentX = current[0];int currentY = current[1];for (int[] dir : dirs) {// 依次表示 上、左、下、右周围四个点的x、y坐标int x = currentX + dir[0];int y = currentY + dir[1];// 如果坐标未越界,且该周围点mat[x][y]未被访问过(由BFS概念可知,先被访问的的mat[i][j]一定不会超过后访问的)// 也可以不使用标记数组,替换为判断 不越界 且 当前点的距离小于周围点(mat[currentX][currentY] < mat[x][y]),但效率却更低些if (x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {// 标记访问过,并入队visited[x][y] = true;queue.offer(new int[]{x, y});// 更新值mat[x][y] = mat[currentX][currentY] + 1;}}}return mat;
}
解题思路与代码实现二
采用动态规划:
先找最优子结构,很明显,一个点的最短距离应该是它周围上下左右四个点(如果存在的话)的最短距离+1,即:

dp[i][j]表示(i,j)到0的最短距离,但由于0所在位置不固定,所以先将dp数组初始化:mat[i][j]为0,则dp[i][j]取0,否则dp[i][j]取20000(最长距离:m+n-1=19999<20000)。然后为分两轮进行比较:
- 第一轮从左到右从上到下扫描mat数组,
dp[i][j]取mat[i-1][j]+1、mat[i][j-1]+1和dp[i][j]的最小值,需要注意下标越界; - 第二轮从右到左从下到上扫描mat数组,
dp[i][j]取mat[i][j+1]+1、mat[i+1][j]+1和dp[i][j]的最小值,需要注意下标越界;
两轮扫描结束后,dp[i][j]表示(i,j)到0的最短距离,即为所求
public int[][] updateMatrix(int[][] mat) {// m、n分别表示矩阵的行数和列数int m = mat.length, n = mat[0].length;// dp数组int[][] dp = new int[m][n];// dp数组初始化for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 19999为1 <= m, n <= 104条件下,可能出现的最大长度 m + n -1dp[i][j] = mat[i][j] == 0 ? 0 : 20000;}}// 先更新左边和上边的最小值for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 判断上边是否越界if (i - 1 >= 0) {dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j]);}// 判断左边是否越界if (j - 1 >= 0) {dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i][j]);}}}// 再更新右边和下边的最小值for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (i + 1 < m) {dp[i][j] = Math.min(dp[i + 1][j] + 1, dp[i][j]);}if (j + 1 < n) {dp[i][j] = Math.min(dp[i][j + 1] + 1, dp[i][j]);}}}return dp;}
参考链接:
【LeetCode】 542. 01 矩阵 动态规划 dp
LeetCode] 542. 01 Matrix 零一矩阵
相关文章:

Leetcode 542. 01 矩阵
542. 01 矩阵-中等 问题描述 给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。 两个相邻元素间的距离为 1 。 示例 1: 输入:mat [[0,0,0],[0,1,0],[0…...
分享一下微信小程序抽奖链接怎么做
标题:微信小程序抽奖链接制作全攻略,轻松玩转营销抽奖活动 一、引言 在当今的数字化时代,抽奖活动已经成为一种高效的市场营销策略,而微信小程序作为一个功能强大的移动端平台,为企业和个人提供了制作抽奖链接的便捷…...
MathType2024破解版激活序列号
MathType序列号是一款针对该软件而制作的激活工具,大家都知道这款软件在官方是需要花钱购买的,不然得话就只能试用。有很多功能都无法正常使用!而本序列号却可以完美的解决这一难题,因为它可以破解并激活“MathType”,…...

简述对 Spring MVC 的理解
SpringMVC 是一种基于 Java 语言开发,实现了 Web MVC 设计模式,请求驱动类型的轻量级 Web 框架。 Spring MVC组件 MVC 架构模式的思想,通过把 Model,View,Controller 分离,将 Web 层进行职责解耦࿰…...
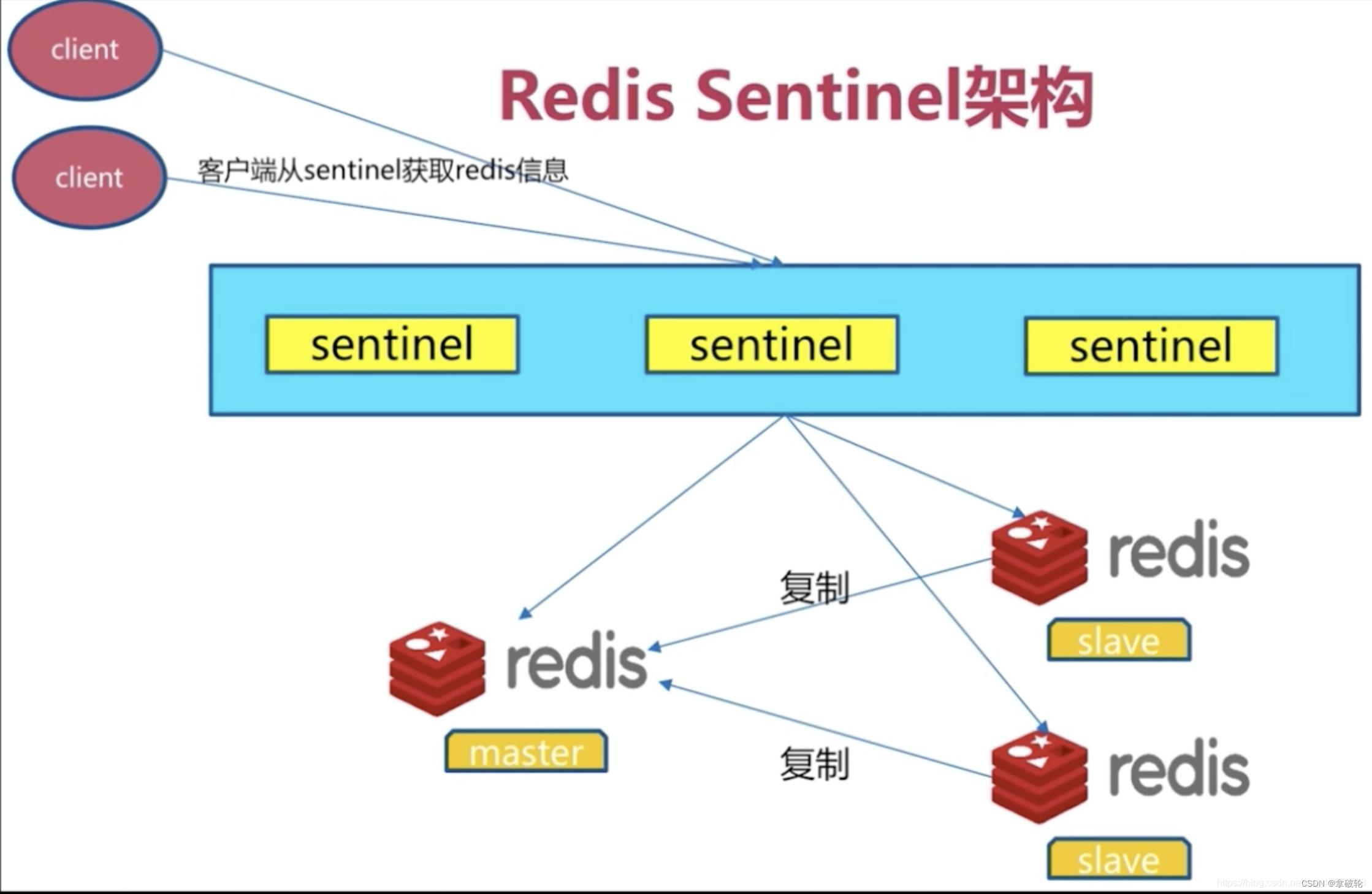
Redis——哨兵模式与Zookeeper选举的异同点
摘要 当我们使用主从复制出现的问题:手动故障转移:写能力和存储能力受限:主从复制 -master 宕机故障处理。 主从切换技术的方法是:当主服务器宕机后,需要手动把一台从服务器切换为主服务器,这就需要人工干…...

基于 Center 的 3D 目标检测和跟踪
论文地址:https://arxiv.org/abs/2006.11275 论文代码:https://github.com/tianweiy/CenterPoint 3D 目标通常表示为点云中的 3D Boxes。 CenterPoint 在第一阶段,使用关键点检测器检测对象的中心,然后回归到其他属性࿰…...
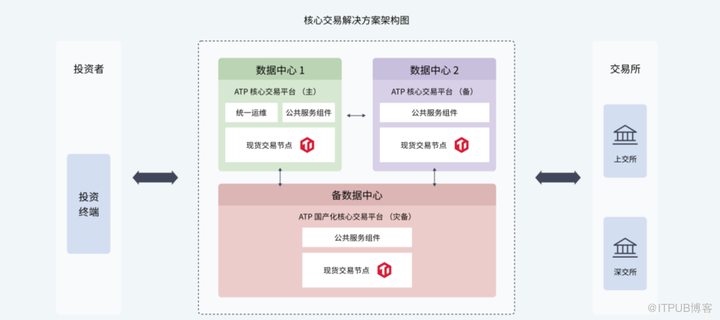
华锐技术何志东:证券核心交易系统分布式改造将迎来规模化落地阶段
近年来,数字化转型成为证券业发展的下一战略高地,根据 2021 年证券业协会专项调查结果显示,71% 的券商将数字化转型列为公司战略任务。 在落地数字化转型战略过程中,证券业核心交易系统面临着不少挑战。构建新一代分布式核心交易…...

数据结构 -- ArrayList与LinkedList的区别
一、二者的相同点 1,它们都是继承自List接口。 二、二者的区别 1,数据结构:ArrayList是(Array动态数组)的数据结构;而LinkedList是(Link双向链表)的数据结构。ArrayList 自由性较…...

豪车托运为什么选小板
小板运输是一种适用于豪车客户的高效运输方式。它提供了快速、安全、便捷的服务,并且相对经济实惠。以下是关于小板运输的时效和价格的介绍: 时效:小板运输通常能够在短时间内完成车辆的运输。具体时效取决于起点和目的地之间的距离ÿ…...

【base64加密】js/ts的基础加密
base64的字符串简单加密,主用于网页缓存数据的加密。 适用于常规html、小游戏(egret、cocos、laya)等 原文参考:JS基于base64编码加密解密文本和图片(修订)_js base64加密-CSDN博客 测试:JS实…...
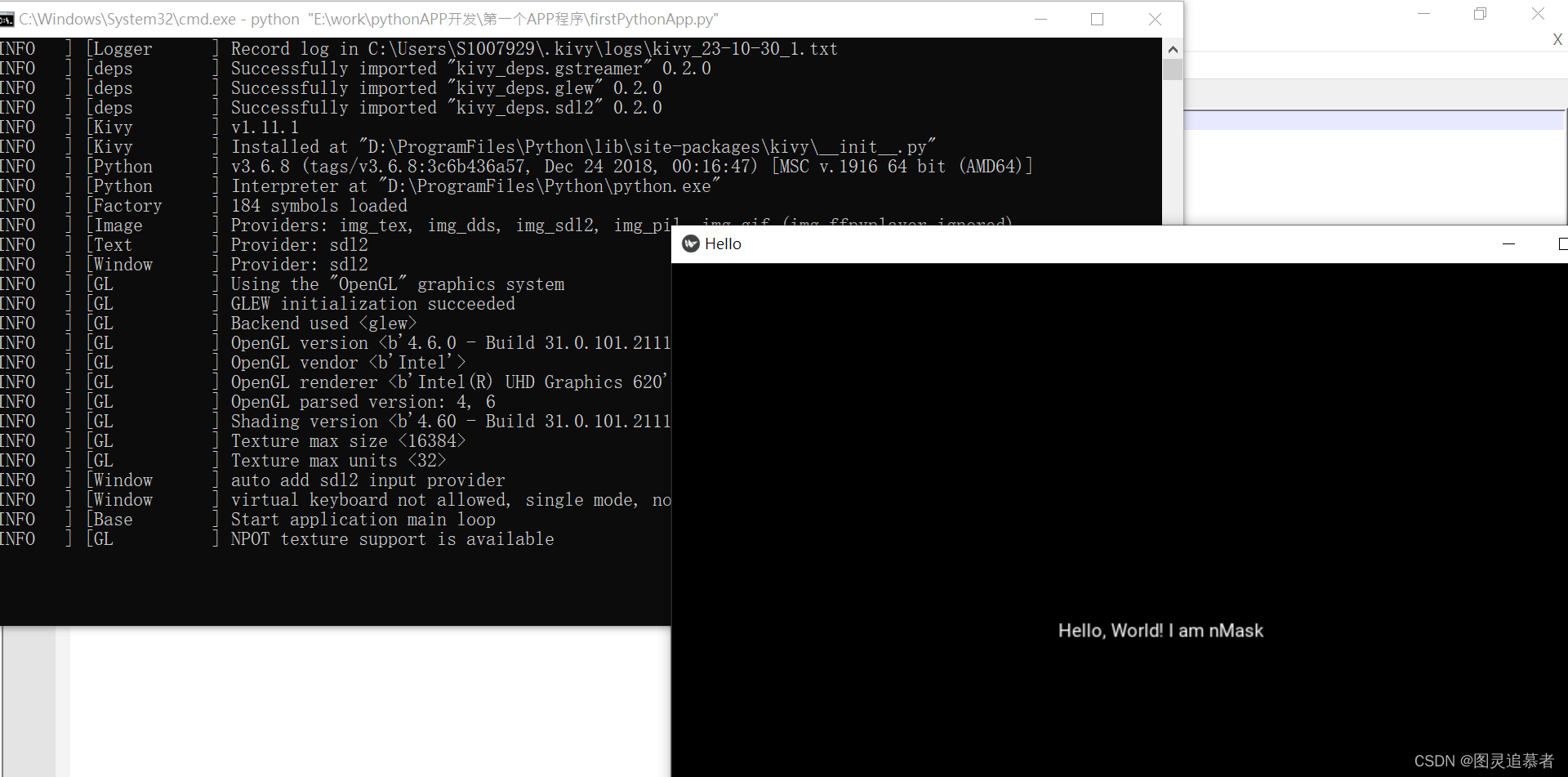
基于python的app程式开发
安装的库文件: 运行代码: # -*- coding:utf-8 -*- from kivy.app import App class HelloApp(App):pass if __name__ __main__:HelloApp().run() 结果画面:...

Spring Event学习
Spring Event学习 观察者模式是一种行为设计模式,它定义了对象之间的依赖关系,当一个对象的状态发生改变时,所有依赖于它的对象都会得到通知并被自动更新。在这个模式中,改变状态的对象被称为主题,依赖的对象被称为观…...

UE4 HLSL学习笔记
在Custom配置对应ush文件路径 在HLSL中写入对应代码 Custom里面增加两个Input,名字必须和ush文件内的未知变量名字一样 然后就对应输出对应效果的颜色 这就是简单的加法运算 减法同理: 乘法除法同理 HLSL取最小值 HLSL取最大值 绝对值: 取余…...
报文的路由过程
路由转发过程 记住路由转发过程结论:报文ip是不变,mac改变。 mac地址在同一个广播域传输过程中是不变的;在跨越广播域的时候会发生改变的;而IP地址在传输过程中是不会改变的(除NAT的时候)。 ip地址本质上是…...

【CPP】类和对象
1- Classes and Objects Structures A struct in C is a type consisting of a sequence of data membersSome functions/Statements are needed to operate the data members of an object of a struct type 不不小心操作错误,不小心越界 Classes You should b…...

【多线程面试题二十】、 如何实现互斥锁(mutex)?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:如何实现互斥锁…...

hypercube背景设置为白色,绘制高光谱3D立方体
import scipy pip install wxpython PyOpenGL和Spectral需要本地安装 可参考链接https://blog.csdn.net/qq_43204333/article/details/119837870 参考:https://blog.csdn.net/Tiandailan/article/details/132719745?spm1001.2014.3001.5506Mouse Functions:left-cl…...
Visual Studio(VS)C++项目 管理第三方依赖库和目录设置
发现很多程序员存在这种做法:把项目依赖的第三方库的lib和dll放在项目目录下,或者复制到输出目录,因为每种配置都有不同的输出目录,所以要复制多份(至少包括Debug和Release两个输出目录),这些做…...

leetCode 2578. 最小和分割 + 排序 + 贪心 + 奇偶分组(构造最优解)
2578. 最小和分割 - 力扣(LeetCode) 给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足: num1 和 num2 直接连起来,得到 num 各数位的一个排列。 换句话说,num1 和 num2 中所…...

自定义实现图片裁剪
要实现这个功能,首先需要创建一个自定义的View,然后在该View中绘制背景框和裁剪后的图片。以下是一个简单的实现: 1. 创建一个名为CustomImageView的自定义View类,继承自View: import android.content.Context; impor…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
