学习笔记|正态分布|图形法|偏度和峰度|非参数检验法|《小白爱上SPSS》课程:SPSS第三讲 | 正态分布怎么检验?看这篇文章就够了
目录
- 学习目的
- 软件版本
- 原始文档
- 为什么要假设它服从正态分布呢?
- t检验
- 一、图形法
- 1、频数分布直方图
- 解读
- 2、正态Q-Q图
- 操作
- 解读
- 3、正态P-P图
- SPSS实战操作
- 解读
- 二、偏度和峰度
- 解读:
- 三、非参数检验法
- 注意事项
- 四、规范表达
- 五、小结
- 划重点
学习目的
SPSS第三讲 | 正态分布怎么检验?看这篇文章就够了
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
为什么要假设它服从正态分布呢?
一方面,是由于正态分布非常普通平凡,所以假设一个随机事件服从正态分布,比假设其他分布的成功率更高。
另一方面,是因为正态分布能够指明探索的方向。比如,如果我们验证后发现,这个随机事件不服从正态分布,那它就一定不满足正态分布背后的中心极限定理。而不满足中心极限定理,我们就能知道——要么是它的影响因素不够多,要么是各种影响因素不相互独立,要么是某种影响因素的影响力太大等等…这时候,接下来的研究也就有了明确的方向。
t检验
正态分布是很多连续型数据比较分析的大前提,比如t检验、方差分析、相关分析以及线性回归等,均要求数据服从正态分布或近似正态分布。
但大多数人进行统计时容易忽略这一重要前提,导致统计效能下降和假阴性风险增加。
为此,在系统讲解推断性统计方法之前,本课程将呈现三种正态分布的检验方法,让我们一次性掌握正态分布的检验方法。
一、图形法
一提到正态分布,我们自然会想到一个钟型形状。如下图。特点是“中间多,两端少”。
那么,怎么检验一组数据是否服从正态分布呢?先呈现个案例。
案例:25名青少年数据如下表,请判断该组数据的身高是否服从正态?
导入数据,命令行:
GET FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第三讲 正态分布.sav'.
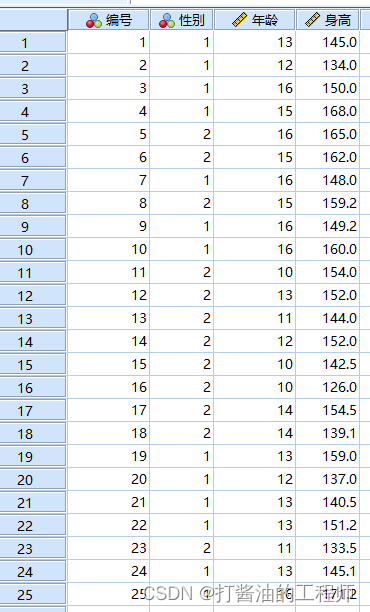
案例分析:身高数据明显属于连续型变量,可进行正态检验。
1、频数分布直方图
SPSS实战操作
第一步:【图形】→【旧对话框】→【直方图】
第二步:弹出直方图,将待分析变量移入【变量】框内,勾选显示正态曲线,本次我们考察“身高”数据,其他参数不用设置,直接【确定】命令执行。确定后,呈现如下直方图。
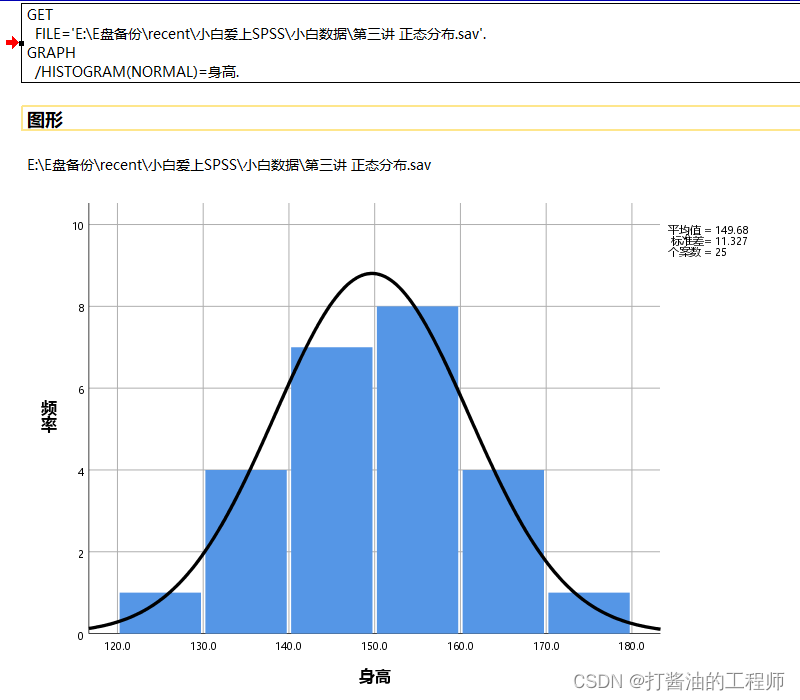
命令行:
GRAPH /*绘图*//HISTOGRAM(NORMAL)=身高. /*直方图(正态)*/
解读
观察直方图的分布形状是否为一个倒扣“钟”型的对称形状,如果接近或相似,则可认为数据服从正态分布。
本例中,“身高”数据频数分布直方图的形状比较接近于倒扣的“钟形”,左右两边具有对称性,可认为该数据为正态分布数据。
执行:GRAPH /HISTOGRAM(NORMAL)=年龄. 显示“年龄”变量的直方图:
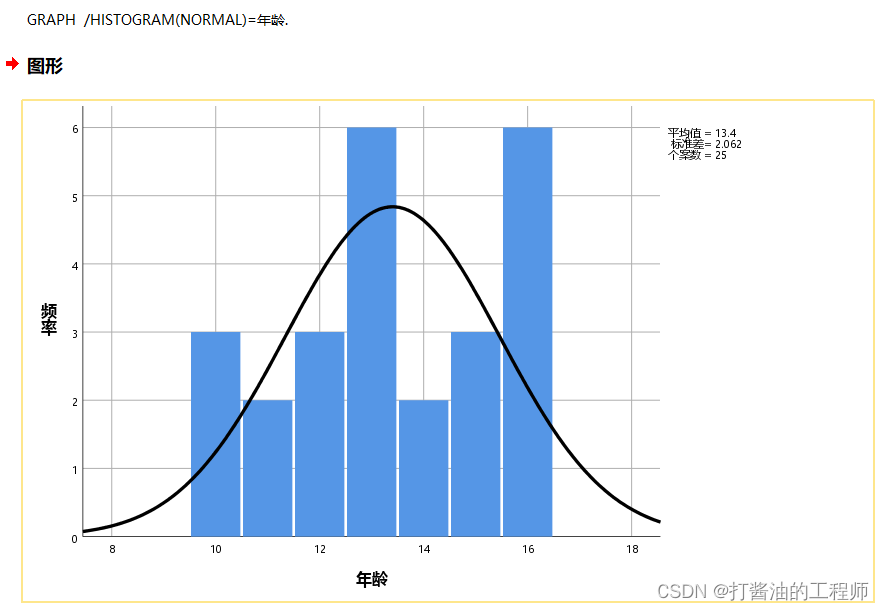
明显与正态曲线不重合。
2、正态Q-Q图
简介:Q-Q图反映了变量的实际分布与理论分布的符合程度,可以用来考察数据是否服从某种分布类型。若数据服从正态分布,则数据点应与理论直线基本重合。
操作
第一步:【分析】→【描述统计】→【QQ图】
第二步:将待分析的连续数据变量,如:身高,移入【变量】框内,软件默认是检验【正态分布】,其他参数不用设置,直接【确定】命令执行。
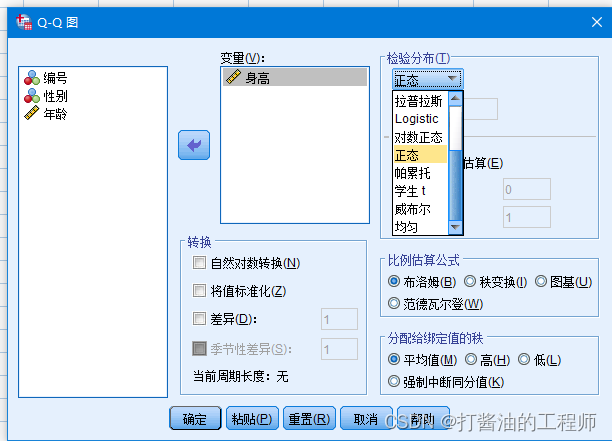
确定后,呈现如下Q-Q图。
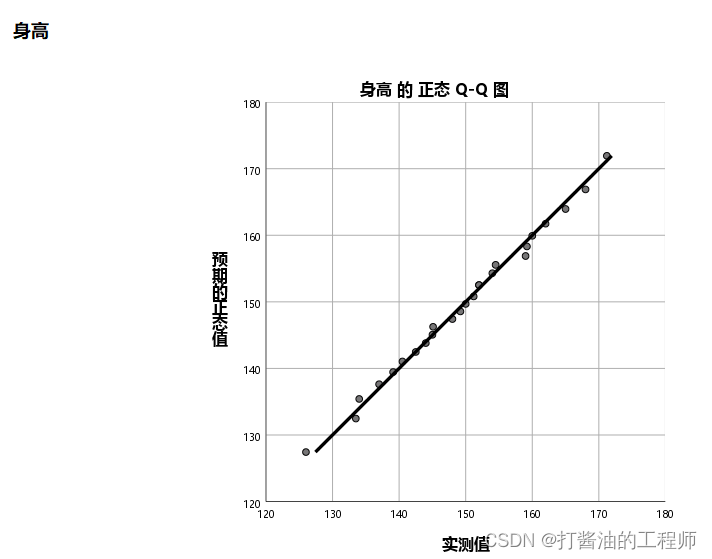
命令行:
···
PPLOT
/VARIABLES=身高 /核心变量,其他行为可选参数,有默认或初始值/
/NOLOG
/NOSTANDARDIZE
/TYPE=Q-Q
/FRACTION=BLOM
/TIES=MEAN
/DIST=NORMAL.
···
解读
观察Q-Q图上的点能否分布在一条直线上,分布在一条直线上则说明近似或服从正态分布。
本例中,身高绝大多数的点能分布在一条直线上,直线趋势明显,可认为该连续数据服从正态分布。
3、正态P-P图
简介:P-P图反映了变量的实际累积概率与理论累积概率的符合程度,可以用来考察数据是否服从某种分布类型。若数据服从正态分布,则数据点应与理论直线基本重合。与Q-Q图意义相似。
SPSS实战操作
第一步:【分析】→【描述统计】→【P-P图】
第二步:将待分析的连续数据变量移入【变量】框内,本例检测“身高”数据的正态分布,软件默认是检验【正态分布】,其他参数不用设置,直接【确定】命令执行。
命令行:
···
PPLOT
/VARIABLES=身高 /核心变量,其他行为可选参数,有默认或初始值/
/TYPE=P-P
/DIST=NORMAL.
···
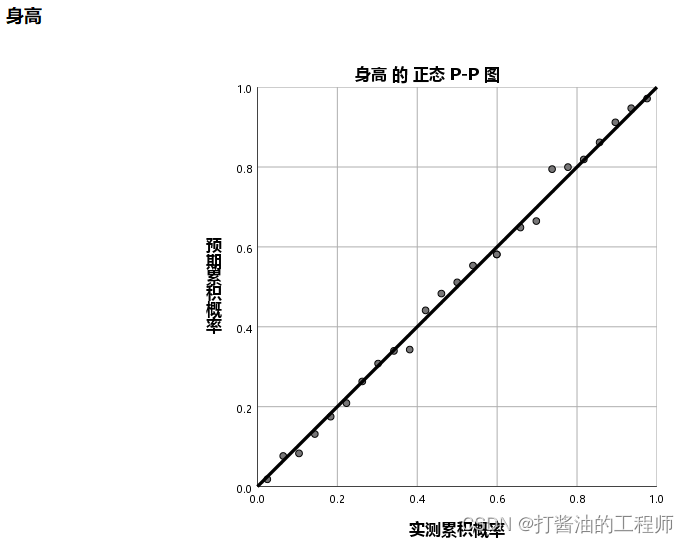
解读
观察P-P图上的点能否分布在理论分布的直线上,若基本分布在直线上则说明近似或服从正态分布。
本例中,“身高”的绝大多数的点能分布在一条直线上,直线趋势明显,可认为该连续数据服从正态分布。
二、偏度和峰度
简介:
[偏度]主要用于判定数据的对称性,整体数据偏左还是偏右,见下图。
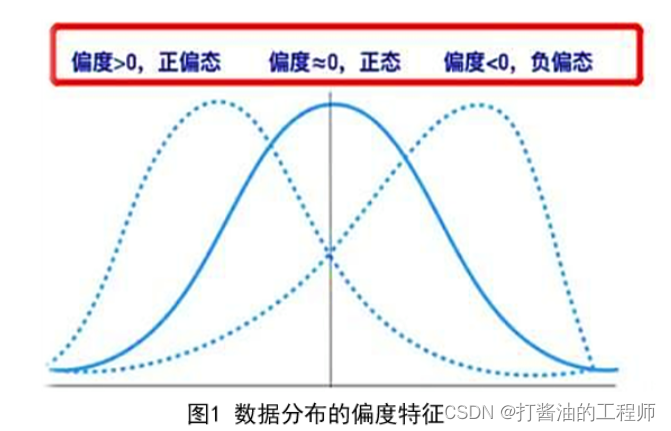
当偏度S≈0时,可认为分布是对称的,服从正态分布;
当偏度S>0时,分布为右偏,即拖尾在右边,峰尖在左边,也称为正偏态;
当偏度S<0时,分布为左偏,即拖尾在左边,峰尖在右边,也称为负偏态;
注意:数据分布的左偏或右偏,指的是数值拖尾的方向,而不是峰的位置。
[峰度]是用于判定数据分布的陡缓程度,见下图。
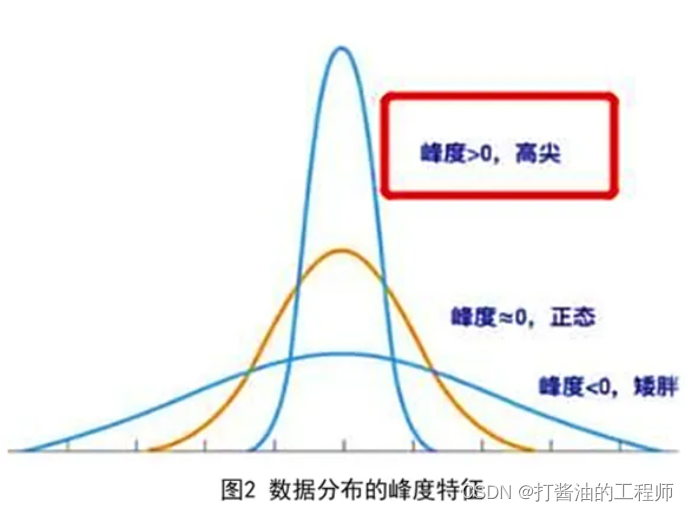
当峰度K≈0时,可认为分布的峰态合适,服从正态分布(不胖不瘦);
当峰度K>0时,分布的峰态陡峭(高尖);
当峰度K<0时,分布的峰态平缓(矮胖);
了解偏度和峰度这两个统计量的含义很重要,是检验数据正态分布的重要指标。
实际上,我们收集到很难能满足S≈0,K≈0, 因此,可采用K与S系数来检验,检验公式如下。
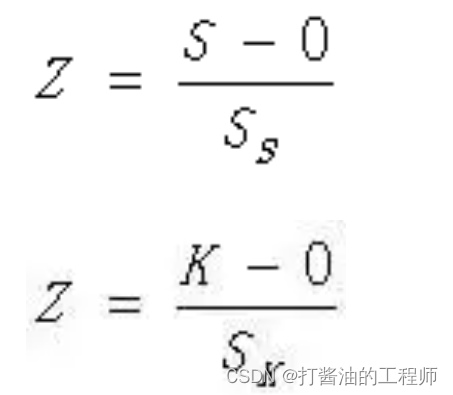
其中,SS和SK均为S系数和K系数的标准误。在α=0.05的情况下,Z值的绝对值大于1.96时,可认为K系数或S系数显著不等于0,即样本数据非正态。
SPSS实战操作
第一步:【分析】→【描述统计】→【描述】
第二步:将“身高”选入【变量】框中,点击【选项】,勾选“平均值”、“标准差”、“峰度”和“偏度”。
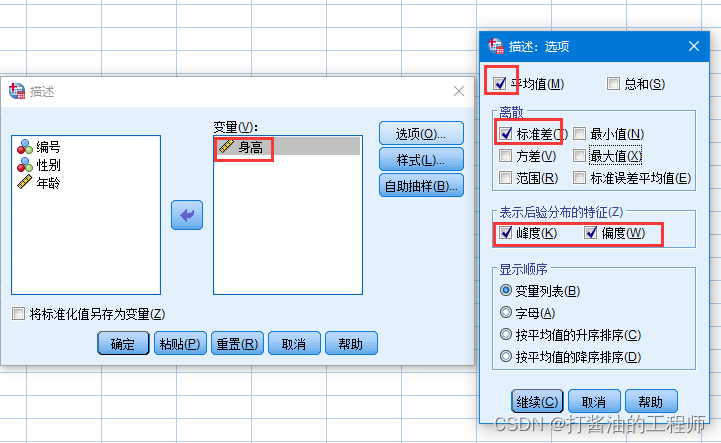
第三步:点击“继续”、“确定”,得到计算结果。
命令行:
···
DESCRIPTIVES VARIABLES=身高
/STATISTICS=MEAN STDDEV KURTOSIS SKEWNESS. /统计指标=平均值 标准差 峰度 偏度/
···
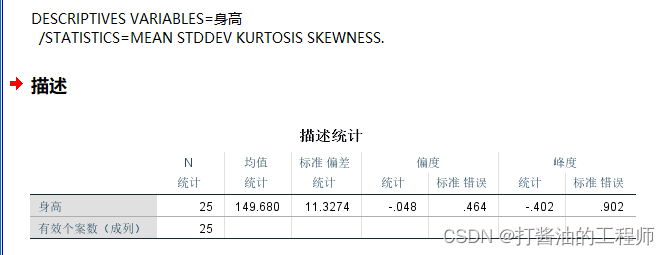
解读:
①计算偏度系数:
手算:
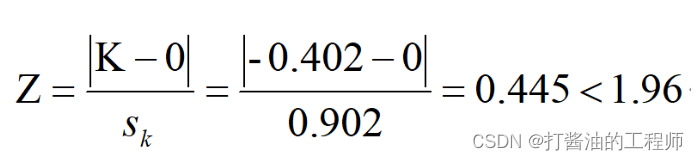
②计算峰度系数:
手算:
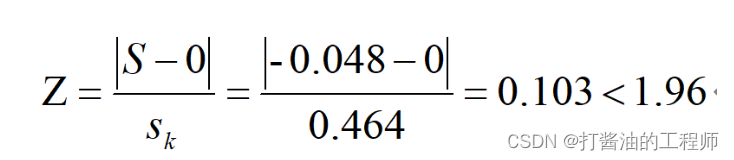
由以上结果可知,偏度系数和峰度系数的绝对值均小于1.96,可以认为该组样本数据符合正态分布。
需注意:当样本量过大(超过100)时,采用峰度和偏度系数会对正态性的情况有所偏误,此时,可以直接尝试采用图示法(直方图、P-P、Q-Q)的方法进行检验会更直观。
三、非参数检验法
简介:正态性检验属于非参数检验,原假设为“样本来自的总体与正态分布无显著性差异”,只有P>0.05才能接受原假设,即数据符合正态分布。
常见的正态性检验有Kolmogorov-Smirnov检验(即柯尔莫戈洛夫-斯米诺夫检验,简称K-S检验)和Shapiro-Wilk检验(即夏皮-威尔克检验,简称S-W检验),K-S检验适用于大样本数据,S-W检验适用于小样本数据,当检验结果的p值小于0.05,则认为数据不满足正态性。
SPSS实战操作
第一步:【分析】-【描述统计】-【探索】 打开探索对话框。
第二步:本例我们想分别检验男女两组的身高是否服从正态分布,故将身高选入【因变量】列表,将性别选入【因子列表】
点击 【图】 --勾选“直方图”“含检验的正态图”
点击【继续】–【确定】,得到探索性分析结果。输出结果有很多图表,我们只解释正态性检验结果。
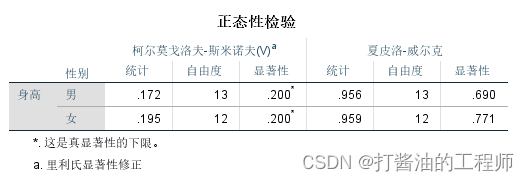
命令行:
EXAMINE VARIABLES=身高 BY 性别 /PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
结果解读:
当数据量≤50时,倾向于以夏皮洛-威尔克(S-W)检验结果为准;
当数据量>50时,倾向于以柯尔莫戈洛夫-斯米诺夫(K-S)检验结果为准;
当数据量>5000时,SPSS只会显示K-S检验结果。
本例中,我们比较25例男女中学生身高差异,需要分别看这两组的身高分布情况,上表显示,两组的样本量(可参考自由度那一列数值)均小于50,故以夏皮洛-威尔克(S-W)检验结果为准.
两组检验的p值(即显著性那一列)分别为0.690、0.771,均大于0.05,说明这两组身高均符合正态分布,故认为身高满足正态性。
注意事项
在使用S-W和K-S检验时需注意,当样本量较少的时候,检验结果不够敏感,即使数据分布有一定的偏离也不一定能检验出来;而当样本量较大的时候,检验结果又会太过敏感,只要数据稍微有一点偏离,P值就会<0.05,检验结果倾向于拒绝原假设,认为数据不服从正态分布。
所以,如果样本量足够多,即使检验结果P<0.05,数据来自的总体也可能是服从正态分布的。为此,我们要结合图直方图、P-P、Q-Q的图示法灵活使用。
四、规范表达
本次测量样本为25名,故采用夏皮洛-威尔克(S-W)检验,将SPSS输出结果整理为三线表,如下表1。
表1 身高的S-W正态性检验结果

从上表可知,男女生的正态性检验结果的统计分别为0.956和0.959,P值分别为0.690、0.771,均大于0.05。
同时结合直方图、P-P图和Q-Q图,可认为男生和女生的身高都服从正态分布。
五、小结
正态分布的检验方法包括图示法、偏度和峰度、非参数检验方法。
图形法检验正态分布往往是有效的,是实际应用中较为普遍的方式,是对正态分布显著性检验(如偏度和峰度的Z值、S-W及K-S检验)的有力辅助手段。
在实际的应用中,往往会出现明明直方图显示分布很对称,但参数检验的结果P值却<0.05,拒绝原假设认为不服从正态分布。
此时建议不要太刻意追求正态性检验的P值,一定要参考直方图、P-P图等图形工具来帮助判断。因此正态性检验三种方法均有重要实用意义。
很多统计学方法,如T检验、方差分析等,与其说要求数据严格服从正态分布,不如说“数据分布不要太偏态”更为合适。
小白学习完本节课内容之后,赶紧回去对40名大侠的数据进行正态性检验(第二讲数据),结果发现大侠们的身高、体重服从正态分布,而成绩不服从正态分布。
身高正态性检验(命令行):
EXAMINE VARIABLES=身高/PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
身高检验结果:
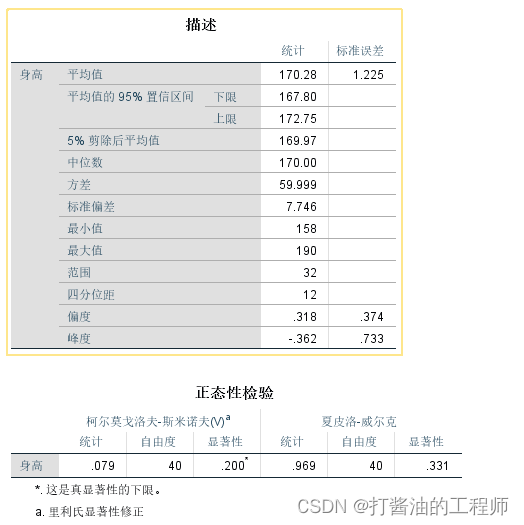
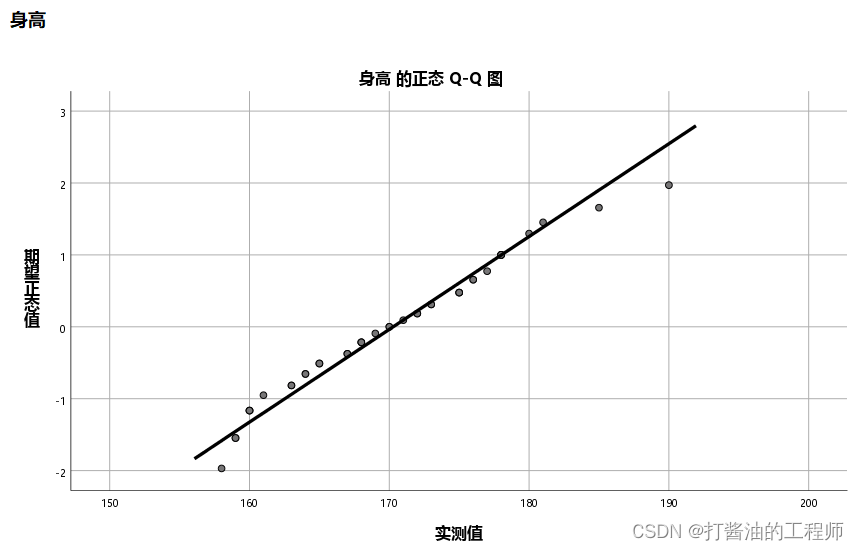
体重正态性检验(命令行):
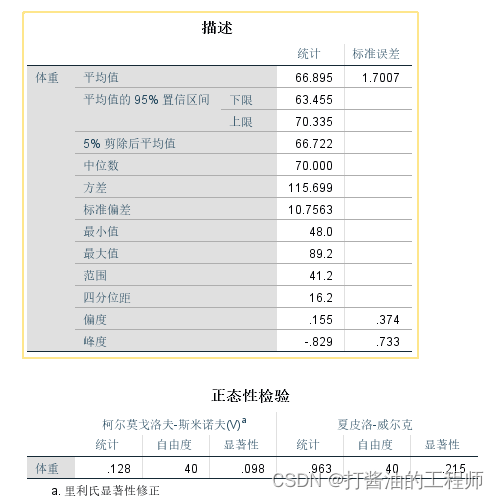
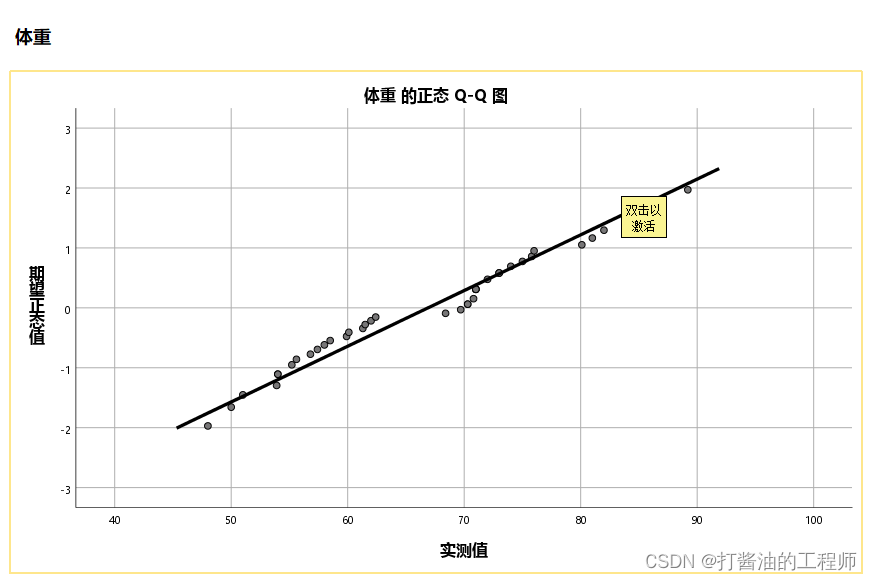
EXAMINE VARIABLES=体重/PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
体重检验结果:
成绩正态性检验(命令行):
EXAMINE VARIABLES=成绩/PLOT BOXPLOT NPPLOT /*若无此行,则不输出正态性检验表*//COMPARE GROUPS /STATISTICS DESCRIPTIVES /CINTERVAL 95 /MISSING LISTWISE /NOTOTAL.
成绩检验结果:
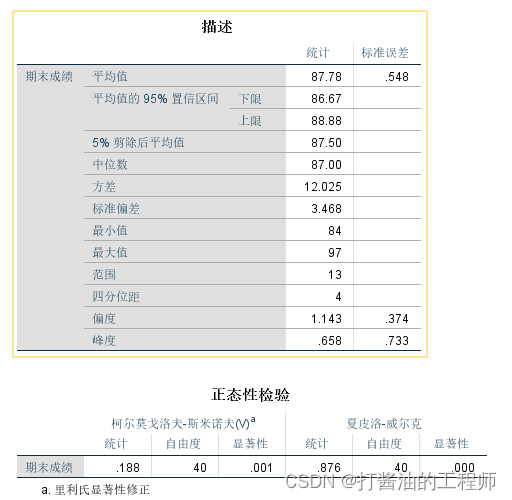
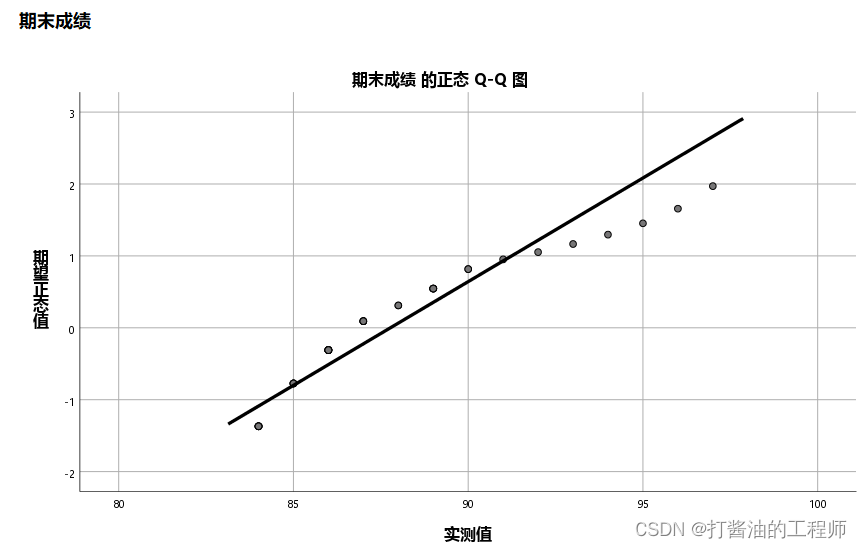
于是,大侠们的身高和体重采用平均数、标准差来描述,而成绩采用中位数和四分位距来描述。
小白把上次的描述性结果呈送给主任,主任看后,满意地点点头。
然后,转过头对小白说:“小白,我想了解下今年这些大侠们的体重是否超标了?如果超标,就要加强训练,减脂减重,你能比较出来吗?”
小白这时比较淡定了,因为他非常清楚,《小白爱上SPSS》课程下一讲,将开启假设检验,讲解差异比较的T检验。
所以,搬好小板凳,等待开课就好了!
划重点
1、正态分布的检验方法包括图示法、偏度和峰度、非参数检验方法。
2、实际应用不必太刻意追求偏峰度的Z值和S-W及K-S检验的P值,需要结合直方图、P-P图和Q-Q图来判断。
3、对于统计方法,与其说要求数据严格服从正态分布,不如说“数据分布不要太偏态”更为合适。
相关文章:

学习笔记|正态分布|图形法|偏度和峰度|非参数检验法|《小白爱上SPSS》课程:SPSS第三讲 | 正态分布怎么检验?看这篇文章就够了
目录 学习目的软件版本原始文档为什么要假设它服从正态分布呢?t检验一、图形法1、频数分布直方图解读 2、正态Q-Q图操作解读 3、正态P-P图SPSS实战操作解读 二、偏度和峰度解读: 三、非参数检验法注意事项 四、规范表达五、小结划重点 学习目的 SPSS第三讲 | 正态…...

Android NDK开发详解之ndk-build 脚本
Android NDK开发详解之ndk-build 脚本 内部原理从命令行调用选项可调试 build 与发布 build要求 ndk-build 脚本使用 NDK 的基于 Make 的构建系统构建项目。我们针对 ndk-build 使用的 Android.mk 和 Application.mk 配置提供了更具体的文档。 内部原理 运行 ndk-build 脚本相…...

应用于智慧矿山的皮带跑偏视频分析AI算法
一、引言 随着科技的发展,人工智能技术已经在各个领域得到广泛应用。而在智慧矿山领域,皮带跑偏视频分析是其中一个重要的应用方向。本文将详细介绍皮带跑偏视频分析AI算法的原理,以期为智慧矿山的发展提供有益的参考。 二、算法原理 1. 视…...

vue3 UI组件优化之element-plus按需导入
如果不在意项目打包体积大小,正常来讲element-plus 是这样用的 import ElementPlus from element-plus //引入样式 import "element-plus/dist/index.css";app.use(ElementPlus);但是呢要是项目就用了几个弹窗提示什么的,全局引入包体积很大 …...
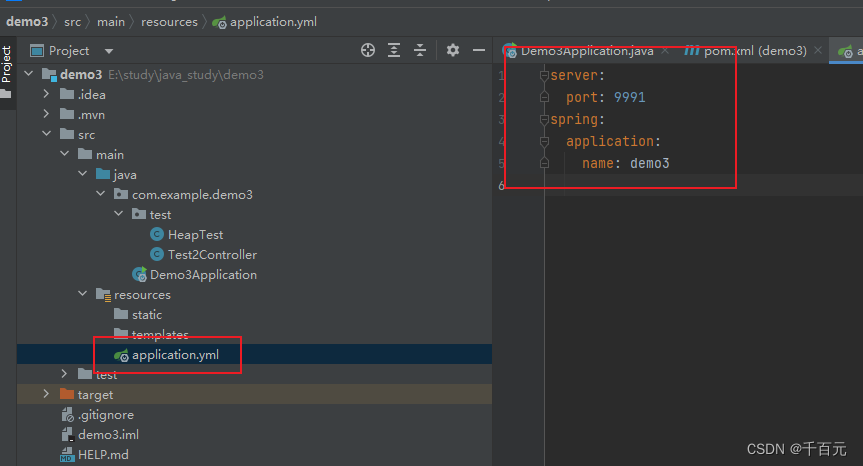
如何创建 Spring Boot 项目
如果有pom.xml有插件异常,可以先删除。 maven配置要配置好 然后yaml,再启动就行 server:port: 9991 spring:application:name: demo3参考 如何创建 Spring Boot 项目_创建springboot项目_良月初十♧的博客-CSDN博客...
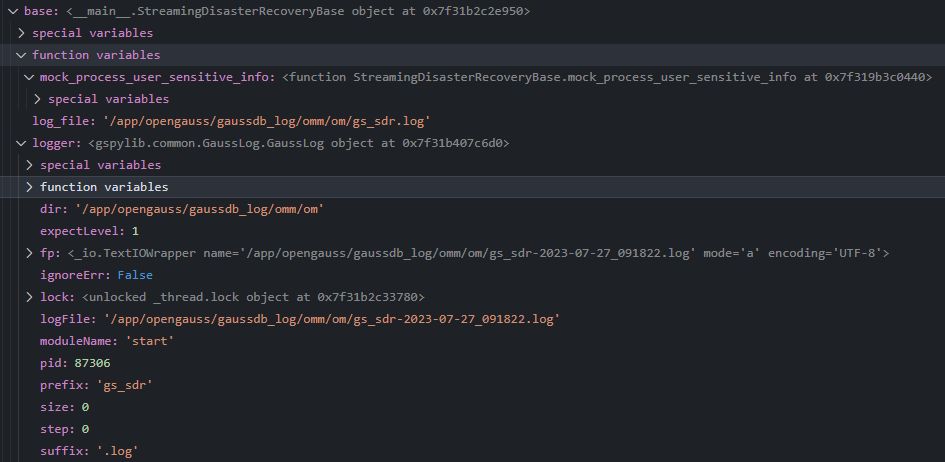
【经验分享】openGauss容灾集群搭建
gs_sdr命令代码解读 背景 openGauss推出了容灾架构,相比之前的一个集群主从架构,而容灾架构是两个集群间的数据同步。为了更深入了解其原理,本文试图通过阅读gs_sdr命令相关的代码来学习下相关的各种操作。 1.容灾搭建过程可以参考…...
)
互联网应用架构的演进(八大架构的演进过程)
文章目录 前言常见概念八大架构演进过程单机架构应用数据分离架构应用服务集群架构读写/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构 前言 博主最近在学中间件,理解互联网应用架构的演进过程,对于理解中间件在整体结构中的定位是十分重…...

ROS自学笔记二十六:导航中激光雷达消息
在ROS导航中,激光雷达(Laser Scanner)通常被用于感知机器人周围的环境,进行障碍物检测和建图,以支持导航。下面是激光雷达的详细介绍以及一个示例: 激光雷达简介: 激光雷达是一种传感器&#…...

分类模型的评价指标
评价指标: 1、准确率 2、精准率 3、召回率 4、f1-Score 5、auc曲线 在了解评价指标在hi前,首先需要了解一种叫做混淆矩阵的东西 混淆矩阵: 真正例TP:本来正确的,分类到正确的类型 伪正例FP:本来是错误的&a…...

第五章 I/O管理 八、缓冲区管理
目录 一、定义 二、缓冲区的作用 三、单缓冲 1、定义: 2、例子1 3、例子2 四、双缓冲 1、定义: 2、例子1: 3、例子2: 五、单缓冲和双缓冲的区别 六、循环缓冲区 1、定义: 七、缓冲池 1、定义:…...
笔记软件推荐!亲测好用的8款笔记软件!
在以往的生活中,我们都需要用纸和笔做笔记,但随着时代的发展,许多人已经不再选择用这种传统方式,来记录自己重要的笔记了,他们都选择将重要的笔记用软件记录下来,将笔记保存在电脑里,更不容易…...

MPJQueryWrapper 用法
// 创建QueryWrapper对象MPJQueryWrapper<WebEvaluation> queryWrapper new MPJQueryWrapper<>();// 设置要查询的字段queryWrapper.select("u.nick_name", "u.avatar_url").select("wu.nick_name as relayToUserName", "ta.c…...

50元买来的iPhone手机刷机经验
前段时间,家里的iPad被家人误操作,导致iPad变成不可使用状态。自己折腾了半天,没有找到解决办法。没有办法,只好拿到手机维修店去修理,很快就修理好了.其实也很简单--就是对iPad进行了刷机操作。当然我也看到了刷机的方法。今天&a…...
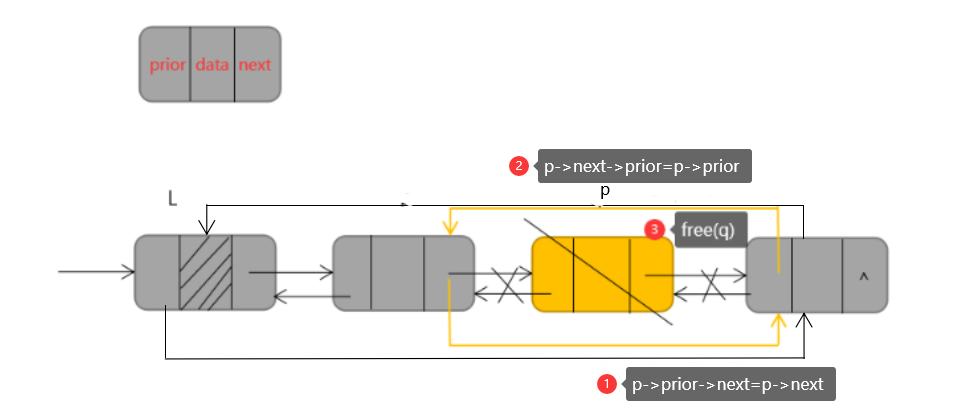
数据结构学习笔记——链式表示中的双链表及循环单/双链表
一、双链表 (一)双链表的定义 双链表是在单链表结点上增添了一个指针域prior,指针域prior指向当前结点的前驱结点,即此时链表的每个结点中都有两个指针域prior和next,从而可以很容易通过后继结点找到前驱结点&#x…...

DC电源模块去除输出电源中的高频噪声及杂波
BOSHIDA DC电源模块去除输出电源中的高频噪声及杂波 DC电源模块是电路中常用的部件,用于提供电子元器件的工作电源。然而,在使用DC电源模块的过程中,往往会出现一些问题,比如输出电源中产生的高频噪声和杂波。这些问题不仅会影响…...

【驱动开发】注册字符设备使用gpio设备树节点控制led三盏灯的亮灭
注册字符设备使用gpio设备树节点控制led三盏灯的亮灭 设备树: 头文件: #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct {unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int OD…...

面向制造企业的持续发展,2023数字化工单管理系统创新篇章-亿发
面向制造企业的持续发展,2023数字化工单管理系统开创新篇章-亿发 随着制造业的持续发展,运维工单管理日益成为关键环节,它设计客户管理、设备维护、服务商合作等多个业务领域,对运营效率和服务质量有着重要影响。然而,…...

mysql 元数据锁 MDL读锁与MDL写锁
事务一开启事务 begin; select * from tablename;--相当于加了MDL读锁 此时事务2执行alter table tablename add ... --会发生修改阻塞 commit; --提交事务 释放MDL读锁 此时事务二修改成功 如果事务一执行做dml操作,操作期间将加MDL写锁...

批量预处理哨兵2影像
批量预处理哨兵2影像 最近下载70多景哨兵2影像,平均每个影像在cmd中处理时间都需要半个小时。算下来我一景一景手动处理需要37个小时左右,每天在电脑前待8个小时也要4天多,很浪费时间。如果能够批处理,不需要我手动做的话&#x…...

Unity地面交互效果——2、动态法线贴图实现轨迹效果
Unity引擎动态法线贴图制作球滚动轨迹 大家好,我是阿赵。 之前说了一个使用局部UV采样来实现轨迹的方法。这一篇在之前的基础上,使用法线贴图进行凹凸轨迹的绘制。 一、实现的目标 先来回顾一下,上一篇最终我们已经绘制了一个轨迹的贴图…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
