没有上司的舞会(C++,树形DP)
题目描述
某大学有 nnn 个职员,编号为 1…n1\ldots n1…n。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 rir_iri
但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
输入格式
输入的第一行是一个整数 nnn。
第 222 到第 (n+1)(n + 1)(n+1) 行,每行一个整数,第 (i+1)(i+1)(i+1) 行的整数表示 iii 号职员的快乐指数 rir_iri。
第 (n+2)(n + 2)(n+2) 到第 2n2n2n 行,每行输入一对整数 l,kl, kl,k,代表 kkk 是 lll 的直接上司。
输出格式
输出一行一个整数代表最大的快乐指数。
样例 #1
样例输入 #1
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
样例输出 #1
5
提示
数据规模与约定
对于 100%100\%100% 的数据,保证 1≤n≤6×1031\leq n \leq 6 \times 10^31≤n≤6×103,−128≤ri≤127-128 \leq r_i\leq 127−128≤ri≤127,1≤l,k≤n1 \leq l, k \leq n1≤l,k≤n,且给出的关系一定是一棵树。
解题思路:
首先,注意题中说的是“如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。”
也就是说间接上司来不来是无所谓的
接下来讲解本题的解题思路
这道题可以算是树形DP的入门级题目了
树形DP,就是在树形结构中采用动态规划
(说了但好像什么都没说)
常规思路就是自顶向下递推,确定叶子节点后,逐级回归更新父节点
那么这道题为什么采用树形DP呢?
首先题目中给出的是一棵树
其次,我们想要知道舞会的最大快乐指数,除了遍历每一种可能外好像别无选择
那么降低时间复杂度就要想到DP,在本题中也就是树形DP
思路很简单,每个职员只有两种状态:来、不来
我们用dp[now][1]表示来,dp[now][0]表示不来
那么有
//树形DP
void dfs(int now) {//参加dp[now][1] = happy[now];//参加,初始化为自己的快乐指数//不参加for (int i = head[now]; i != -1; i = edges[i].next) {//遍历子节点int v = edges[i].v;dfs(v);//返回后更新dp[now][0] += max(dp[v][0], dp[v][1]);//不参加,需要累加子节点来的情况dp[now][1] += dp[v][0];//参加,需要累加子节点不来的情况}
}
最后,AC代码如下
#include <iostream>
#include <string.h>
using namespace std;
const int max_n = 6e3;
const int min_r = -128;
const int max_r = 127;int n, u, v;
int happy[max_n + 1];
int in[max_n + 1];
//链式前向星
struct edge { int v, next; }edges[max_n + 1];
int head[max_n + 1];
int tot = -1;
//树形DP
long long dp[max_n + 1][2];//存边
void add_edge(int u, int v) {edges[++tot] = { v,head[u] }; head[u] = tot;
}//树形DP
void dfs(int now) {//参加dp[now][1] = happy[now];//参加,初始化为自己的快乐指数//不参加for (int i = head[now]; i != -1; i = edges[i].next) {//遍历子节点int v = edges[i].v;dfs(v);//返回后更新dp[now][0] += max(dp[v][0], dp[v][1]);//不参加,需要累加子节点来的情况dp[now][1] += dp[v][0];//参加,需要累加子节点不来的情况}
}int main() {memset(head + 1, -1, sizeof(int) * max_n);cin >> n;for (int i = 1; i <= n; i++) cin >> happy[i];for (int i = 1; i < n; i++) {//存图cin >> u >> v;add_edge(v, u);//反向存边,自顶向下in[u]++;}for (int i = 1; i <= n; i++)if (!in[i]) {//从根节点开始dfs(i);cout << max(dp[i][0], dp[i][1]) << endl;break;}return 0;
}相关文章:
)
没有上司的舞会(C++,树形DP)
题目描述 某大学有 nnn 个职员,编号为 1…n1\ldots n1…n。 他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。 现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 ri…...
【java基础】static和final关键字的作用及其用法详解
文章目录static关键字静态字段静态方法静态代码块静态内部类final关键字final字段final方法final类static关键字 这个关键字表示静态的,用于不同地方意思不一样 静态字段 如果我们将其作用到字段上,那么该字段为类所拥有,我们使用new关键字…...

#集成学习#:bagging、boosting、stacking和blending
集成学习是一种机器学习方法,旨在提高单个模型的性能和鲁棒性。它基于这样一个假设:通过结合多个模型的预测结果,可以获得更好的预测性能,因为每个模型都可能从数据中提取不同的信息,因此他们的错误也可能是不同的&…...

NCRE计算机等级考试Python真题(一)
第一套试题1、关于数据的存储结构,以下选项描述正确的是A.数据所占的存储空间量B.数据在计算机中的顺序存储方式C.数据的逻辑结构在计算机中的表示D.存储在外存中的数据正确答案: C2、关于线性链表的描述,以下选项中正确的是A.存储空间不一定…...

C#协变逆变
文章目录协变协变接口的实现逆变里氏替换原则协变 协变概念令人费解,多半是取名或者翻译的锅,其实是很容易理解的。 比如大街上有一只狗,我说大家快看,这有一只动物!这个非常自然,虽然动物并不严格等于狗…...

算法设计与分析期末考试复习(四)
贪心算法(Greedy Algorithm) 找零钱问题 假设有4种硬币,面值分别为:二角五分、一角、五分和一分,现在要找给顾客六角三分钱,如何找使得给出的硬币个数最少? 首先选出1个面值不超过六角三分的最…...
)
qsort函数排序数据 and 模拟实现qosrt函数(详解)
前言:内容包括使用库函数qsort排序任意类型的数据,模拟实现qsort函数(冒泡排序的逻辑) 我们先了解qsort函数的语法:qsort函数默认按照升序排序数据 void qsort (void* base, size_t num, size_t size,int (*compar)(…...

Mysql视图,存储过程,触发器,函数以及Mysql架构
一,视图视图是基于查询的一个虚拟表 , 也就是将sql语句封装起来, 要用的时候直接调用视图即可, select语句查询的表称为基表, 查询的结果集称为虚拟表, 基本表数据发生了改变, 那么视图也会发生改变, 使用视图就是为了简化查询语句.1.CREATE VIEW view_admin AS SELECT * FROM…...
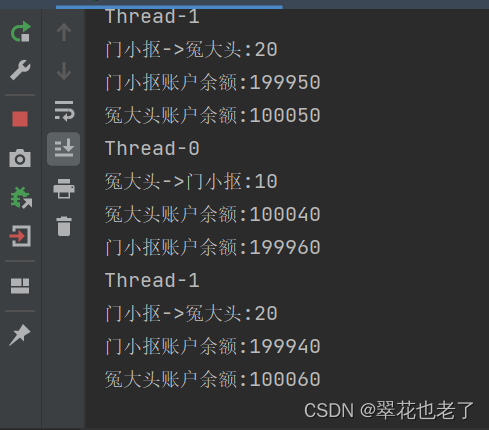
什么是线程死锁?如何解决死锁问题
死锁,一组互相竞争的资源的线程之间相互等待,导致永久阻塞的现象。 如下图所示: 与死锁对应的,还有活锁,是指线程没有出现阻塞,但是无限循环。 有一个经典的银行转账例子如下: 我们有个账户类…...
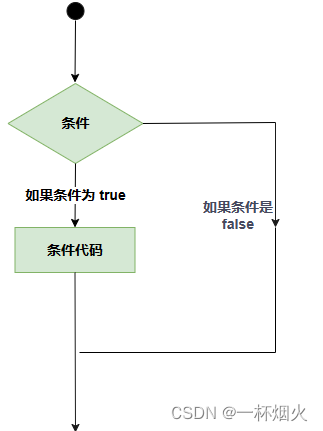
C语言几种判断语句简述
C 判断 判断结构要求程序员指定一个或多个要评估或测试的条件,以及条件为真时要执行的语句(必需的)和条件为假时要执行的语句(可选的)。 C 语言把任何非零和非空的值假定为 true,把零或 null 假定为 fals…...

【python学习笔记】:SQL常用脚本(二)
11、四舍五入ROUND函数 ROUND ( numeric_expression , length [ ,function ] ) function 必须为 tinyint、smallint 或 int。 如果省略 function 或其值为 0(默认值),则将舍入 numeric_expression。 如果指定了0以外的值,则将截…...

【Linux】进程地址空间
文章目录🎪 进程地址空间🚀1.写时拷贝与虚拟地址🚀2.地址空间引入🚀3.地址空间的意义⭐3.1 虚拟地址寻址⭐3.2 虚拟地址意义🎪 进程地址空间 地址空间(address space)表示任何一个计算机实体所…...

Qt音视频开发17-vlc内核回调拿图片进行绘制
一、前言 在众多播放器中,支持的种类格式众多,并支持DVD影音光盘,VCD影音光盘及各类流式协议,提供了sdk进行开发,这点是至关重要的,尽管很多优秀的播放器很牛逼,由于没有提供sdk第三方开发&…...

安装配置DHCP
本次实验采用CentOS71.检查在安装DHCP之前先使用rpm命令查看系统中已有的DHCP软件包rpm -qa | grep dhcp由此可知,系统中尚未安装DHCP软件包2.安装我们可以使用yum命令为系统安装DHCP软件包yum -y install dhcp安装完成后再次检查可以看到DHCP软件包3.配置dhcp配置文…...

MarkDown中写UML图的方法
目录序UML图之顺序图顺序图的四个要素关于消息箭头的语法Mermaid中顺序图的简单例子样例用小人表示对象为对象设置别名激活对象UML图之类图类图中常见的关系关于不同类型关系的语法Mermaid中类图的简单例子样例类定义的两种方式为类定义成员双向关系的表示多重性关系的表示UML之…...

Axure8设计—动态仪表盘
本次分享的的案例是Axure8制作的动态仪表盘,根据设置的数值,仪表盘指针旋转到相应的值位置 预览地址:https://2qiuwg.axshare.com 下载地址:https://download.csdn.net/download/weixin_43516258/87502161 一、制作原型 1、首先创建空白页…...
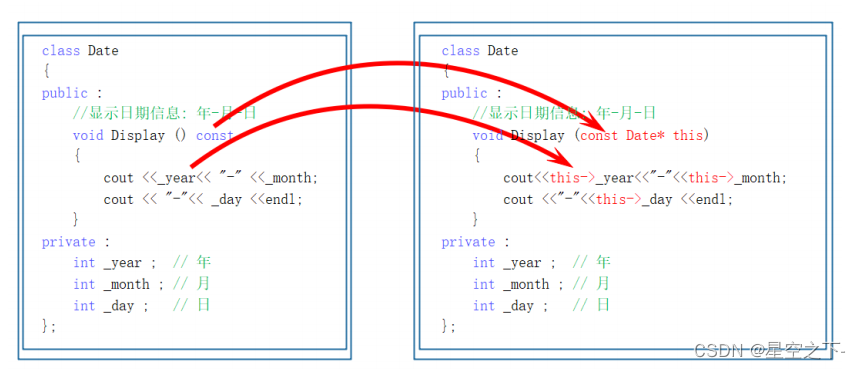
【C++】类和对象的六个默认成员函数
类的6个默认成员函数构造函数概念特性析构函数概念特性拷贝构造函数概念特征拷贝构造函数典型调用场景:赋值运算符重载运算符重载赋值运算符重载取地址及const取地址操作符重载类的6个默认成员函数 到底什么是类的6个默认成员函数呢?相信大家一定对此怀…...
4、算法MATLAB---认识矩阵
认识矩阵1、矩阵定义和基本运算1.1 赋值运算符:1.2 等号运算符:1.3 空矩阵1.4 一行一列矩阵1.5 行矩阵(元素用空格或逗号分隔)1.6 列矩阵(分号表示换行)1.7 m行n列的矩阵:行值用逗号间隔&#x…...
vue3+rust个人博客建站日记2-确定需求
反思 有人说过我们正在临近代码的终结点。很快,代码就会自动产生出来,不需要再人工编写。程序员完全没用了,因为商务人士可以从规约直接生成程序。 扯淡!我们永远抛不掉代码,因为代码呈现了需求的细节。在某些层面上&a…...

Linux安装云原生网关Kong/KongA
目录1 概述2 创建服务器3 安装postgres4 安装kong5 安装node6 安装KONGA1 概述 Kong Kong是一款基于OpenResty(NginxLua模块)编写的高可用、易扩展的开源API网关,专为云原生和云混合架构而建,并针对微服务和分布式架构进行了特别…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
