4、算法MATLAB---认识矩阵
认识矩阵
- 1、矩阵定义和基本运算
- 1.1 赋值运算符:=
- 1.2 等号运算符:==
- 1.3 空矩阵
- 1.4 一行一列矩阵
- 1.5 行矩阵(元素用空格或逗号分隔)
- 1.6 列矩阵(分号表示换行)
- 1.7 m行n列的矩阵:行值用逗号间隔,换列用分号间隔
- 1.8 生成矩阵
- 使用冒号运算符
- 使用linspace函数
- 1.9 矩阵的拼凑
- 行拼接
- 列拼接
- 1.10 矩阵的变形
- 2、特殊矩阵
- 2.1 单位矩阵
- 2.2 全0矩阵
- 2.3 全1矩阵
- 2.4 三维矩阵
- 3、随机矩阵
- 3.1 随机数矩阵
- 3.2 随机整数矩阵
- 3.3 randn用法同rand
1、矩阵定义和基本运算
1.1 赋值运算符:=
a = 1;
b = 2;
c = a+b;
1.2 等号运算符:==
逻辑运算符:返回0或1
a == 1;
a == b;
1.3 空矩阵
m = [];
1.4 一行一列矩阵
m= [1];
1.5 行矩阵(元素用空格或逗号分隔)
m2 =[1 2 3];
或
m3 = [4,5,6];
1.6 列矩阵(分号表示换行)
m4 = [1;2;3];
1.7 m行n列的矩阵:行值用逗号间隔,换列用分号间隔
m5 = [1,2,3; 4 5 6];

1.8 生成矩阵
使用冒号运算符
m=初始值:步长:终值(步长默认为1)
m6=1:10;

m7=1:0.5:10;

使用linspace函数
m = linspace(初始值,终值,点数)(点数默认是100)
linspace(1,10,100)

1.9 矩阵的拼凑
行拼接
m2 =[1 2 3];
m3 = [4,5,6];
m8=[m2,m3];
运行m8的值如下

列拼接
m2 =[1 2 3];
m3 = [4,5,6];
m8=[m2;m3];
运行m8的值如下

1.10 矩阵的变形
reshape(矩阵,要变成的形状)
m6=1:10;
reshape(m6,[2,5])

2、特殊矩阵
2.1 单位矩阵
eye(n)
n为阶数
n = 3;
eye(n);

2.2 全0矩阵
zeros(n) ----------------------------------- n为阶数%
zeros( m,n) 或zeros( [m,n]) ---------- m为行数,n为列数
n = 3;
zeros(n);

zeros(3,5);
zeros([3,5]);

2.3 全1矩阵
ones(n)------------------n为阶数%
ones([m,n])------------- m为行数,n为列数
ones(n);
ones([2,3]);

2.4 三维矩阵
应用:
黑白图像(二维矩阵)
彩色图像(三维矩阵,RGB三个通道,每个通道都是一个二维矩阵)
ones([3,5,2]);
%行、列、页

3、随机矩阵

3.1 随机数矩阵
rand:0-1之间的随机数(返回的数服从城分布)
rand(n): n阶
rand([m,n]): m为行数,n为列数



3.2 随机整数矩阵
randi(max): [1,max]的整数
randi(max, n): n阶矩阵,元素范围1-max
randi(max,[m,n]): m*n矩阵,元素范围1-max



3.3 randn用法同rand

相关文章:

4、算法MATLAB---认识矩阵
认识矩阵1、矩阵定义和基本运算1.1 赋值运算符:1.2 等号运算符:1.3 空矩阵1.4 一行一列矩阵1.5 行矩阵(元素用空格或逗号分隔)1.6 列矩阵(分号表示换行)1.7 m行n列的矩阵:行值用逗号间隔&#x…...
vue3+rust个人博客建站日记2-确定需求
反思 有人说过我们正在临近代码的终结点。很快,代码就会自动产生出来,不需要再人工编写。程序员完全没用了,因为商务人士可以从规约直接生成程序。 扯淡!我们永远抛不掉代码,因为代码呈现了需求的细节。在某些层面上&a…...

Linux安装云原生网关Kong/KongA
目录1 概述2 创建服务器3 安装postgres4 安装kong5 安装node6 安装KONGA1 概述 Kong Kong是一款基于OpenResty(NginxLua模块)编写的高可用、易扩展的开源API网关,专为云原生和云混合架构而建,并针对微服务和分布式架构进行了特别…...
)
Vue学习笔记(2)
2.1 事件处理 2.1.1 事件监听器 JavaScript:通过获取DOM对象再往DOM对象上使用addEventListener注册监听事件 const btn document.querySelector(#my-button) btn.addEventListener(click, function() {alert(点击事件!) })jQuery:通过$选择器绑定对象…...

2023年三月份图形化四级打卡试题
活动时间 从2023年3月1日至3月21日,每天一道编程题。 本次打卡的规则如下: 小朋友每天利用10~15分钟做一道编程题,遇到问题就来群内讨论,我来给大家答疑。 小朋友做完题目后,截图到朋友圈打卡并把打卡的截图发到活动群…...

Python操作Excel
Python中对Excel文件的操作包括:读、写、修改。如果要对其进行如上的操作需要导入Python的第三方模块:xlrd、xlwd、xlutils,其分别对应Python的读、写、修改的操作 一、安装Python的第三方模块 二、操作Excel的基本步骤 1、导入响对应的模…...
 C. Serval and Toxel‘s Arrays【统计次数,算贡献】)
Codeforces Round #853 (Div. 2) C. Serval and Toxel‘s Arrays【统计次数,算贡献】
链接 传送门 分析 这道题想法其实很简单,样例的计算方法一定要看懂。以样例1为例,根据他的操作方法可以得到两个新的数组,和一个原来的数组,总共三个数组。 1 2 3 4 2 3 4 5 3 他们两两配对去重,求出总的value。由于每…...
微信小程序-1:比较两数的大小
程序来源》微信小程序开发教程(第二章) 主编:黄寿孟、易芳、陶延涛 ISBN: 9787566720788 程序运行结果: <!--index.wxml--> <view class"container"> <text>第一个数字:&…...
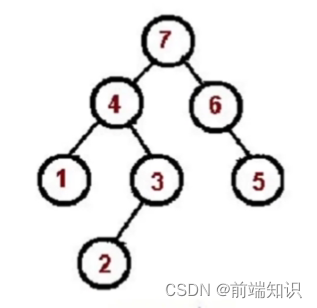
数据结构——树
深度优先/广度优先遍历深度优先:访问根节点对根节点的 children 挨个进行深度优先遍历const tree {val: "a",children: [{val: "b",children: [{val: "d",children: [],},{val: "e",children: [],},],},{val: "c&quo…...

【华为OD机试模拟题】用 C++ 实现 - 找到它(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1) 文章目录 最近更新的博客使用说明找到它题目输入输出示例一输入输出示例二输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD …...

python中yield的使用
在 Python 中,yield 是一个关键字,它用于定义生成器函数。生成器函数是一个特殊的函数,可以返回一个迭代器,当生成器函数被调用时,它不会立即执行,而是返回一个生成器对象,通过迭代生成器对象可…...
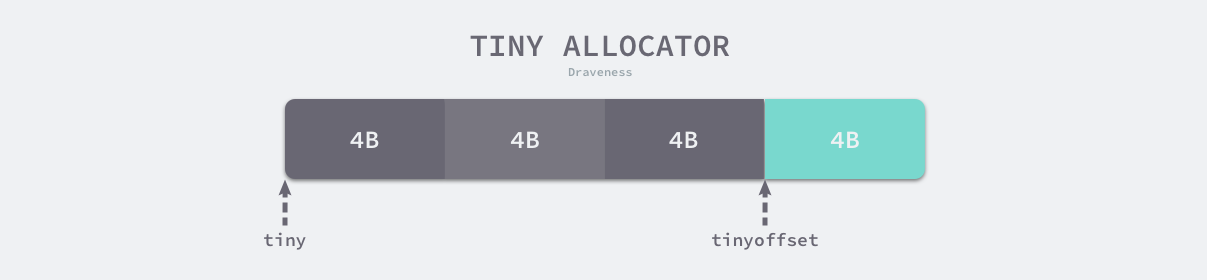
GO进阶(4) 深入Go的内存管理
Go语言成为高生产力语言的原因之一自己管理内存:Go抛弃了C/C中的开发者管理内存的方式,实现了主动申请与主动释放管理,增加了逃逸分析和GC,将开发者从内存管理中释放出来,让开发者有更多的精力去关注软件设计ÿ…...
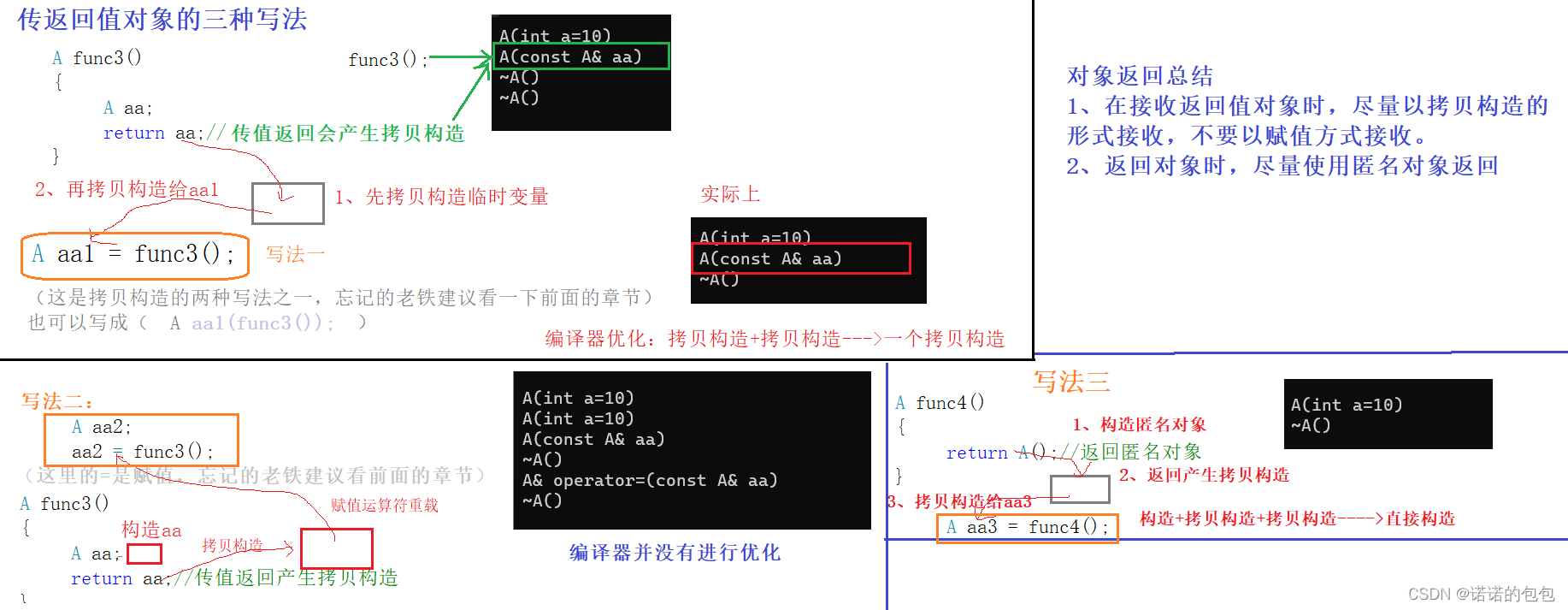
【C++】类与对象理解和学习(下)
放在专栏【C知识总结】,会持续更新,期待支持🌹建议先看完【C】类与对象理解和学习(上)【C】类与对象理解和学习(中)本章知识点概括Ⅰ本章知识点概括Ⅱ初始化列表前言在上一篇文章中,…...

【Neo4j】Spring Data Neo4j APi阅读随笔
引言 关于Spring boot整合Neo4j的官方api翻译&学习随笔 (TOC) 一、准备工作 1.注入依赖 <dependency><groupId>org.springframework.data</groupId><artifactId>spring-data-jpa</artifactId></dependency>2.配置yml文件 这里是本…...

JVM内存模型简介
1 程序计数器 程序计数器是一块较小的内存空间,可以看作是当前线程所执行的字节码的行号指示器。字节码解释器工作时通过改变这个计数器的值来选取下一条需要执行的字节码指令,分支、循环、跳转、异常处理、线程恢复等功能都需要依赖这个计数器来完。 ja…...

k8s如何给node添加标签
一、为什么需要标签? k8s集群如果由大量节点组成,可将节点打上对应的标签,然后通过标签进行筛选及查看,更好的进行资源对象的相关选择与匹配 二、怎么查看目前node上具有的标签 [rootmaster01 ~]# kubectl get node --show-labels NAME …...
【大数据Hive】Hive ddl语法使用详解
一、前言 使用过关系型数据库mysql的同学对mysql的ddl语法应该不陌生,使用ddl语言来创建数据库中的表、索引、视图、存储过程、触发器等,hive中也提供了类似ddl的语法。本篇将详细讲述hive中ddl的使用。 二、hive - ddl 整体概述 在Hive中,DA…...
)
Connext DDS录制服务 Recording Service(2)
2.4 远程管理 控制客户端(如RTI管理控制台)可以使用此接口远程控制录制服务。 注:记录服务远程管理基于第10.3节中描述的RTI远程管理平台。有关录制服务中远程管理工作的详细讨论,请参阅该手册 下面是所有支持操作的API引用。 2.4.1 启用远程管理 默认情况下,在录制服务中…...

mysql数据类型选择
数据类型选择 完整性约束 是完整性约束是为保证数据库中数据的正确性和相容性,对关系模型提出的某种约束条件或规则。 通常包括:实体完整性约束、参照完整性约束、域完整性约束、用户自定义完整性约束。 实体完整性(Entity integrity)是指主键必须非空…...

【Java】Spring Boot 配置文件
文章目录SpringBoot 配置文件1. 配置文件的作用2. 配置文件的格式3. properties配置文件说明3.1 properties基本语法3.2 读取配置文件3.3 properties缺点分析4. yml配置文件说明4.1 yml基本语法4.2 yml使用进阶4.2.1 yml配置不同的数据类型及null4.2.1 yml配置的读取4.2.2 配置…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
