51单片机复位电容计算与分析(附带Proteus电路图)
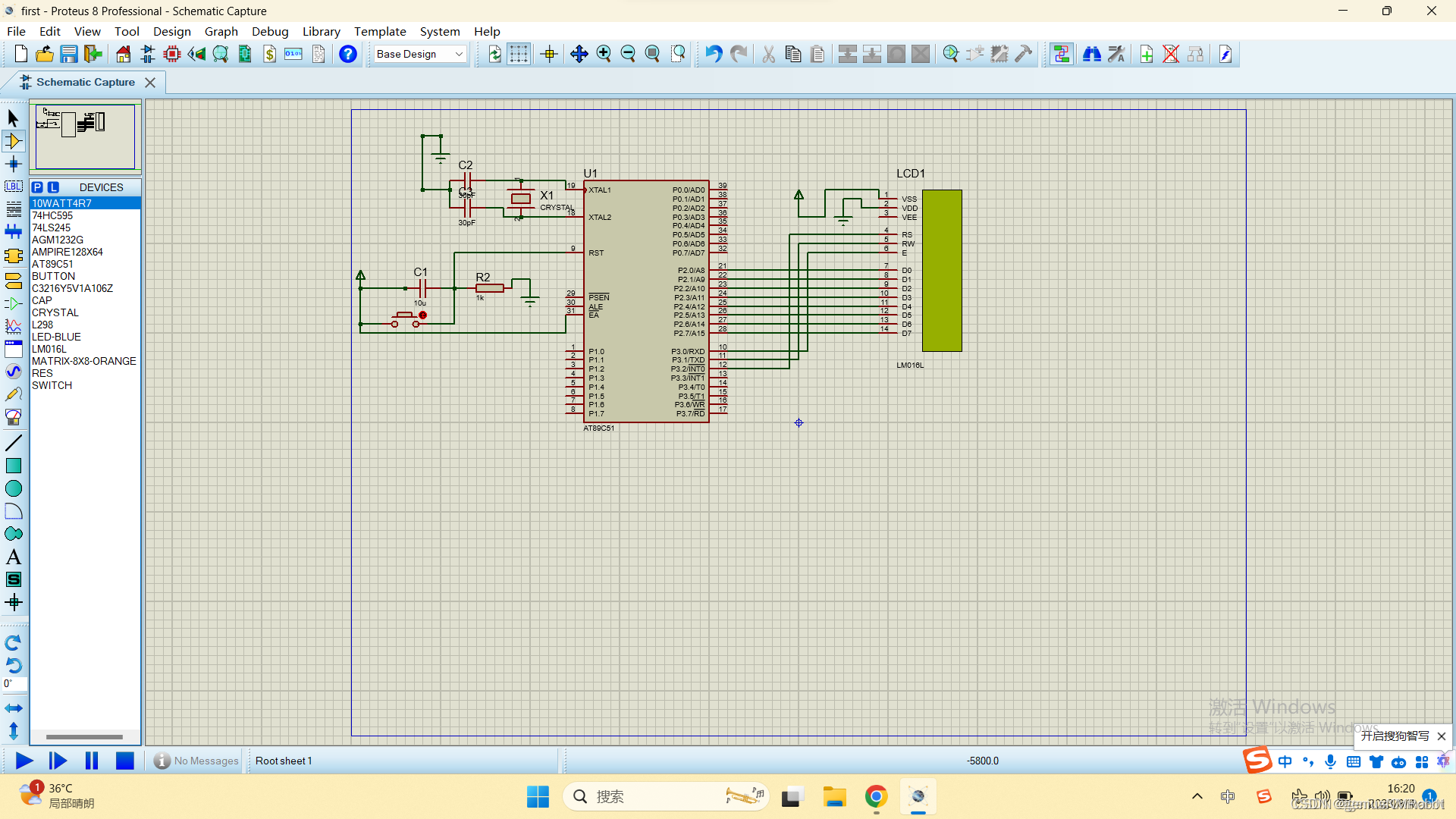
因为i=C x (dU/dt).在上电瞬间,U从0变化到U,所以这一瞬间就是通的,然后这就是一个直流回路,因为电容C直流中是断路的,所以就不通了。
然后来分析一下这个电容的电压到底是能不能达到单片机需要的复位电压。
这是一个线性电容,所以电压变化率是一条直线:

上面那个曲线是我搞错了,对不起啊。
因为我们不知道单片机内部结构。所以来假设一下:
假设电路图是这样的:
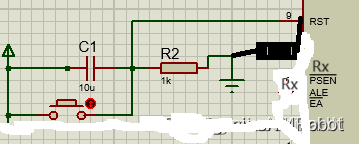
那么可以通过分析电路知道:
R2与Rx并联的电阻为Ra=(R2 X Rx)/(R2+Rx);
单片机此刻电压为:U=电流I x Ra=5-电容电压Uc;
而电容电压Uc在趋近于0的时间点,是近视与0的即Uc=0;
所以此刻单片机感受到的电压U=供电电源的电压=5V;
证明完毕谢谢
相关文章:

51单片机复位电容计算与分析(附带Proteus电路图)
因为iC x (dU/dt).在上电瞬间,U从0变化到U,所以这一瞬间就是通的,然后这就是一个直流回路,因为电容C直流中是断路的,所以就不通了。 然后来分析一下这个电容的电压到底是能不能达到单片机需要的复位电压。 这是一个线性电容&…...

前端性能瓶颈崩溃项目?Webpack助力解决!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、背…...

纷享销客BI,助力企业激活数据价值,科学企业决策
10月25日上午,国家数据局正式挂牌成立,这标志着我国数字经济发展将进入新的发展阶段,也将有力促进数据要素技术创新、开发利用和有效治理,以数据强国支撑数字中国的建设。伴随数据作为企业新的生产要素的意义不断凸显,…...
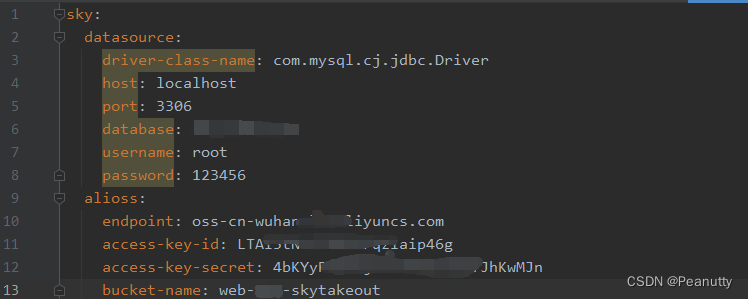
SpringBoot整合阿里云OSS对象存储
文章目录 1、OSS介绍及开通1.1、阿里云OSS简介1.2、开通OSS 2、创建存储空间bucket及密钥获取2.1、创建存储空间2.2、获取密钥 3、OSS快速入门案例4、在springboot项目中整合4.1、将oss配置放到yml文件中4.2、创建Oss属性类,接收yml文件中的属性4.3、封装文件上传功…...
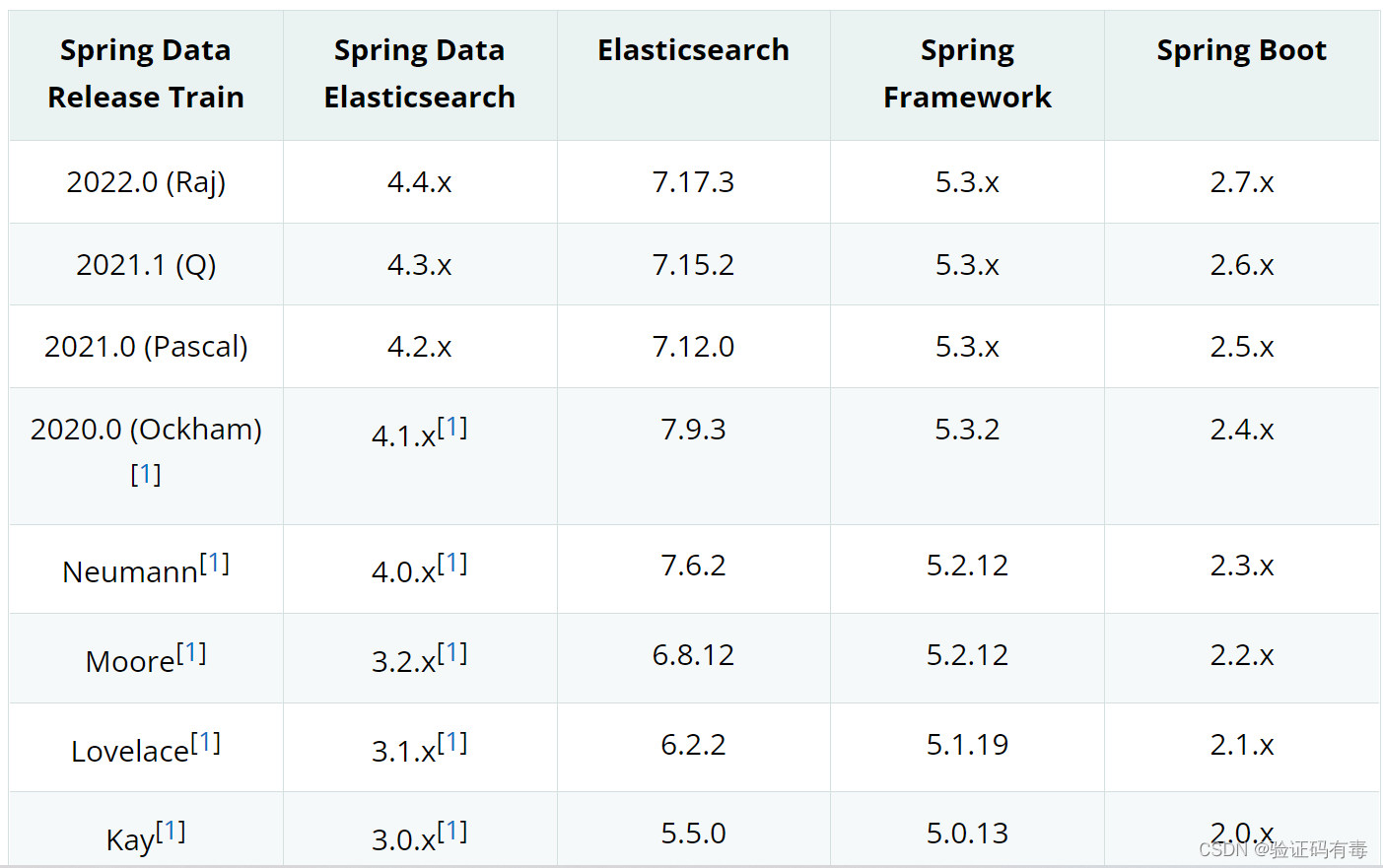
【ES专题】ElasticSearch快速入门
目录 前言从一个【搜索】说起 阅读对象阅读导航笔记正文一、全文检索1.1 什么是【全文检索】1.2 【全文检索】原理1.3 什么是倒排索引 二、ElasticSearch简介2.1 ElasticSearch介绍2.2 ElasticSearch应用场景2.3 数据库横向对比 三、ElasticSearch环境搭建3.1 Windows下安装3.2…...

案例分析真题-质量属性
案例分析真题-质量属性 2009 年真题 【问题1】 【问题2】 2011 年真题 【问题1】 骚戴理解:首先要知道这样的题目没有可靠性,只有可用性,更没有容错性,这里我(3)写成了i,而不是f,仔…...

微信小程序面试题之理论篇
本文内容,来源于极客学院的分享,这里只做引用。 说说你对微信小程序的理解?优缺点? 背景 小程序与H5 优缺点 优点:缺点: 说说微信小程序的生命周期函数有哪些? 应用的生命周期页面的生命期组件的生命周期执行过程 应…...

C++前缀和算法的应用:统计上升四元组
C前缀和算法的应用:统计上升四元组 本文涉及的基础知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 题目 给你一个长度为 n 下标从 0 开始的整数数组 nums ,它包含 1 到 n 的所有数字,请你返回上…...

华泰证券:新奥能源:零售气待恢复,泛能与智家仍是亮点
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,由于新奥能源(02688)发布三季度经营数据: 1-3Q23:天然气零售量yoy-4.7%,燃气批发量yoy17.6%,综合能源销量yoy34.2%ÿ…...
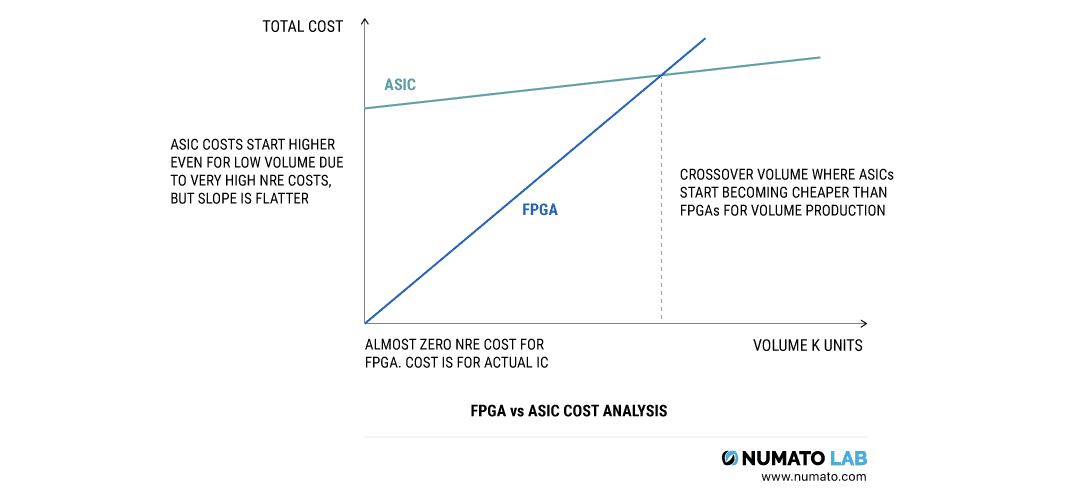
FPGA与ASIC有什么差异?二者该如何选用?
前言 对于一个数字电路的新手来说,这可能是会经常遇到的一个问题:FPGA和ASIC之间的区别是什么? 接下来本文将尝试讲解 “什么是FPGA?” 和 “什么是ASIC?”,然后讲述一些关于FPGA和ASIC的问题,例如它们之间…...

Kotlin run 用法
Kotlin 中的 .run 函数可以用于不同的场景,下面是一些常见的用法: 执行代码块并返回结果: val result run {// 在这里编写一些代码逻辑// 返回最后一个表达式的结果"Hello, Kotlin" }println(result) // 输出:Hello, …...
iZotope RX 10(音频修复和增强工具)
iZotope RX 10是一款音频修复和增强软件,主要特点包括: 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等…...
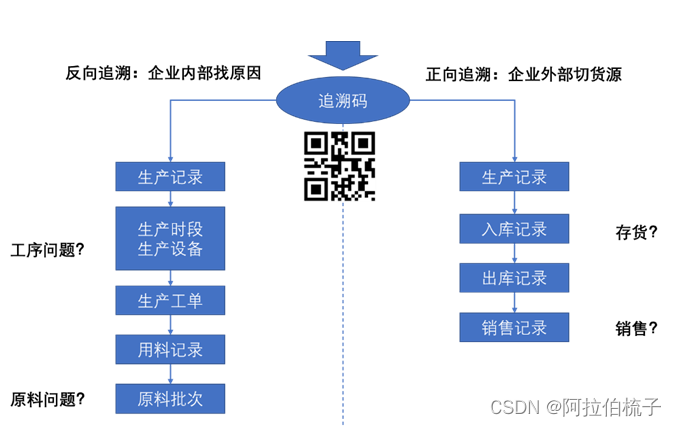
MES 价值点之数据追随
在现代制造业中,数据追溯已经越来越得到重视,特别是那些推行精益生产的企业重要性就更加突出了,而制造执行系统(MES)作为一种关键的生产管理工具,是能很好的为制造企业提供数据追溯功能。今天,和…...

yolo8制作自己的数据集训练和预测分割
一、训练coco128-seg数据集,增加一个类别 coco128-seg数据集下载: github链接 csdn链接 1、修改两个配置文件 (1)、修改"E:\python\ultralytics-main\ultralytics\cfg\datasets\coco128-seg.yaml"路径下的coco128-seg.yaml数据集配置文件,可以拷贝出来 修改数…...
分享一下怎么做一个同城配送小程序
如何制作一个同城配送小程序:功能特点、使用指南及未来展望 一、引言 随着互联网的快速发展,人们对于生活服务的需求越来越高。同城配送作为连接消费者与商家的桥梁,越来越受到人们的关注。本文将详细介绍如何制作一个同城配送小程序&#…...
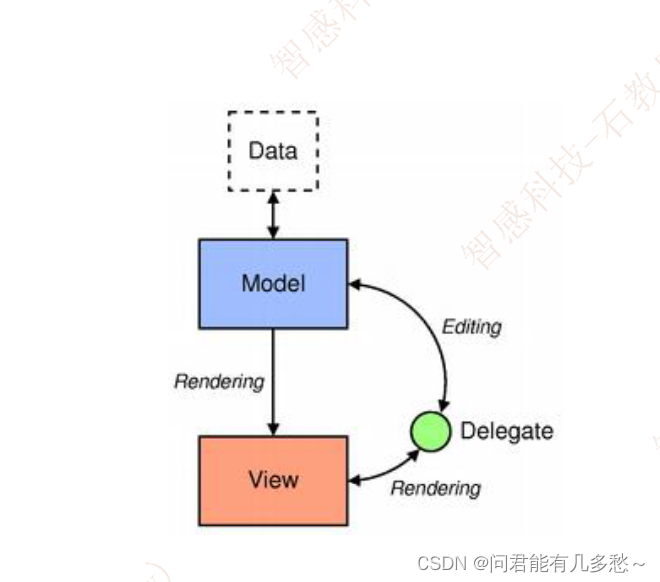
Qt 中model/View 架构 详解,以及案例实现相薄功能
model/View 架构 导读 我们的系统需要显示大量数据,比如从数据库中读取数据,以自己的方式显示在自己的应用程序的界面中。早期的 Qt 要实现这个功能,需要定义一个组件,在这个组件中保存一个数据对象,比如一个列表。我们对这个列表进行查找、插入等的操作,或者把修改…...

提高微星笔记本Linux下散热性能,MSI-EC 驱动新补丁发布
导读近日消息,今年早些时候,Linux 6.4 中添加了 MSI-EC 驱动程序,允许对 Linux 系统微星笔记本电脑进行更多控制。 MSI-EC 驱动程序近日迎来新补丁,为微星笔记本带来 Cooler Boost 功能。该功能允许提高笔记本电脑的风扇转速&…...

Apache Doris (五十): Doris表结构变更-动态分区(2)
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录...

AntDB数据库荣获 “2023年信创物联网优秀服务商”
日前,在2023世界数字经济大会暨第十三届智博会 2023京甬信创物联网产融对接会上,AntDB数据库再获殊荣,获评“2023年信创物联网优秀服务商”。 图1:2023年信创物联网优秀服务商颁奖现场 信创物联网是信息技术应用创新与物联网的结…...
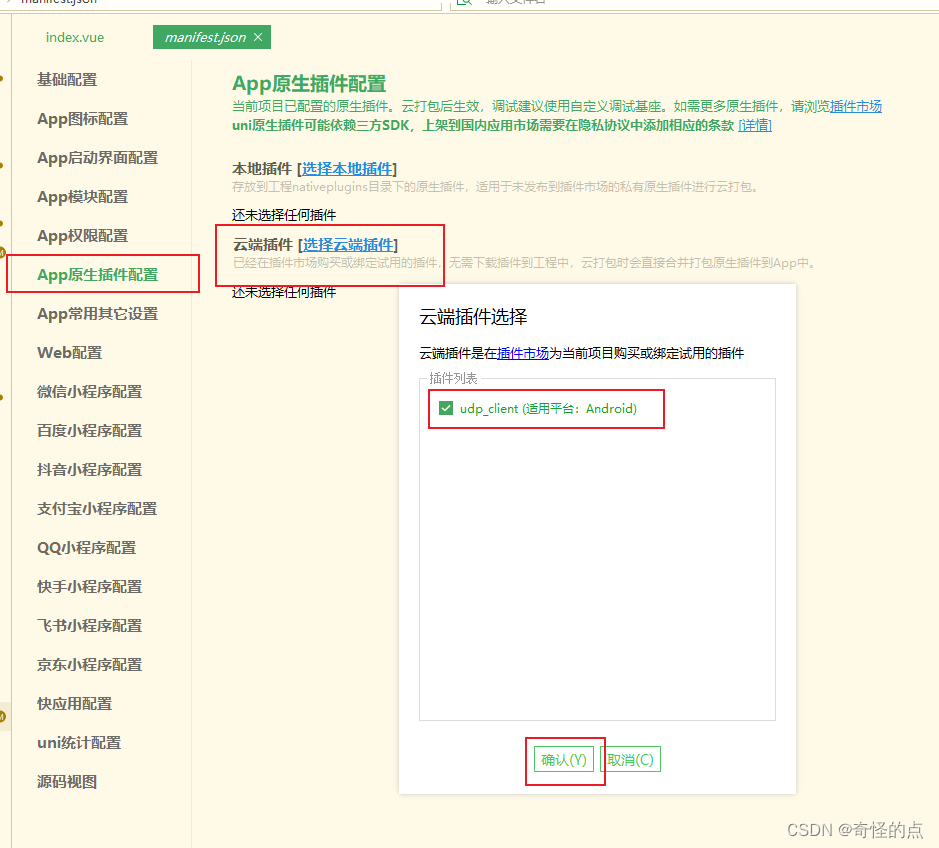
uniapp 使用 UDP
一、搭建UDP服务端,nodejs const dgram require("dgram");const message Buffer.from("你好,这是一个UDP广播消息"); const port 3000; // 用你想要的端口替换这里// 创建一个UDP套接字 const socket dgram.createSocket("…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
