P3983 赛斯石(赛后强化版),背包
题目背景
白露横江,水光接天,纵一苇之所如,凌万顷之茫然。——苏轼
真程海洋近来需要进购大批赛斯石,你或许会问,什么是赛斯石?
首先我们来了解一下赛斯,赛斯是一个重量单位,我们用si作为其单位。比如11赛斯就是1si。
而赛斯石有这样一个性质,它本来是一赛斯一赛斯单独存在的,但是用自然枪将其精化之后,它就会与其它经过精化的赛斯石进行合并,合并到合适的重量之后,便将其钝化,使其不再合并其它赛斯石,如果合错了,也可以用金刚刀将其切开(神奇的是你只能切成整数赛斯重量)。赛斯石的重量只能是整数赛斯重量,而不同赛斯重量的赛斯石的价格也是不一样的。
题目描述
现需上市Need赛斯重量的赛斯石,卖家想算出这些赛斯石经过某种合并方式来获得的最大收益。然而目前有一个问题,市场在真程大殿附近(真程海洋中心位置),卖家需要租船送赛斯石过去(即不考虑卖家自己租船过去的费用),目前有十种船可以租,载重量从1si到10si,每艘船的租价也是有所不同的,如下表所示:
![]()
由于真程大殿附近有强烈的赛斯力,导致无法对赛斯石进行任何操作,商家将赛斯石运过来之后就只能按照之前合并好的卖。假设卖家不返回,且这些赛斯石全部能卖出去。现在卖家他要计算总盈利(设总盈利=赛斯石的总收益-租船所需总费用),请你设计一个程序,算出一种最佳方案,以获得最大总盈利。
输入格式
输入一共有两行
第一行有一个数据Need(赛斯石的总量,单位:si)
第二行有十个数据a1 ... a10(分别为1si到10si的赛斯石市场价格,单位:元)
输出格式
输出仅一行,包含一个整数,表示最大总盈利。
输入输出样例
输入 #1复制
11 1 6 11 17 23 27 33 35 38 43
输出 #1复制
32
输入 #2复制
7 1 5 14 18 20 28 31 34 39 42
输出 #2复制
21
说明/提示
样例一说明:
将11个单位赛斯石合并为一个4si的赛斯石和一个7si的赛斯石并且租两个载重分别为4si和7si的船,这样做为最佳方案,那么最大总盈利就是32元。
注意:
对于所有输入数据,均在区间(0,100000)中,并且为整数;
保证卖家最大总盈利为正;
同一行中,每两个数据之间有一个空格。
赛后强化版于2020年10月13日19点18分已强化完毕。
解析:背包
性质1:对于总重为x的赛斯石我们发现它可以通过载重为 y,z 的船进行运输
性质2: 一艘船可以运多种不同重量的赛斯石,如载重为5 的船可以运输重量为2 和3 赛斯的赛斯石(我最开始就忽略了这点)
根据以上两点性质可以对集合进行状态的划分,不过这里需要进行两次dp,第一次先算出每艘船的最大收益,再dp出每个重量对应的最大收益,可以看看这个方法是否行的通。
对船的收益进行dp:
a[i] 表示重量为 i 的船的最大收益+w[i],易知,这是一个不重不漏的划分方式
状态下转移方程为:a[i]=max( a[i-j]+v[j] , a[i] );
当然,最后还需要 a[i]-=w[i];
对重量对应的最大收益进行dp:
f[i] 表示重量为 i 的赛斯石的最大收益,易知,这也是个不重不漏的划分
状态转移方程:f[i]= max ( f[i-j]+a[j] , f[i] );
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e5 + 5, M = 1e3 + 5;
int w[12] = {0,1,3,5,7,9,10,11,14,15,17 };
int n;
LL v[12], f[N],a[20];int main() {cin >> n;for (int i = 1; i <= 10; i++) {scanf("%lld", &v[i]);}for (int i = 1; i <= 10; i++) {for (int j = 1; j <= i; j++) {a[i] = max(a[i], a[i - j] + v[j]);}}for (int i = 1; i <= 10; i++) {a[i] -= w[i];}for (int i = 1; i <= n; i++) {for (int j = 1; j <= min(i,10); j++) {f[i] = max(f[i], f[i - j]+a[j]);}}cout << f[n] << endl;return 0;
}
相关文章:

P3983 赛斯石(赛后强化版),背包
题目背景 白露横江,水光接天,纵一苇之所如,凌万顷之茫然。——苏轼真程海洋近来需要进购大批赛斯石,你或许会问,什么是赛斯石? 首先我们来了解一下赛斯,赛斯是一个重量单位,我们用…...

系统架构设计师历年真题案例知识点汇总
常见的软件质量属性有多种,例如性能(Performance)、可用性(Availability)、可靠性(Reliability)、健壮性(Robustness)、安全性(Security)、可修改性(Modification)、可变性(Changeability)、易用…...
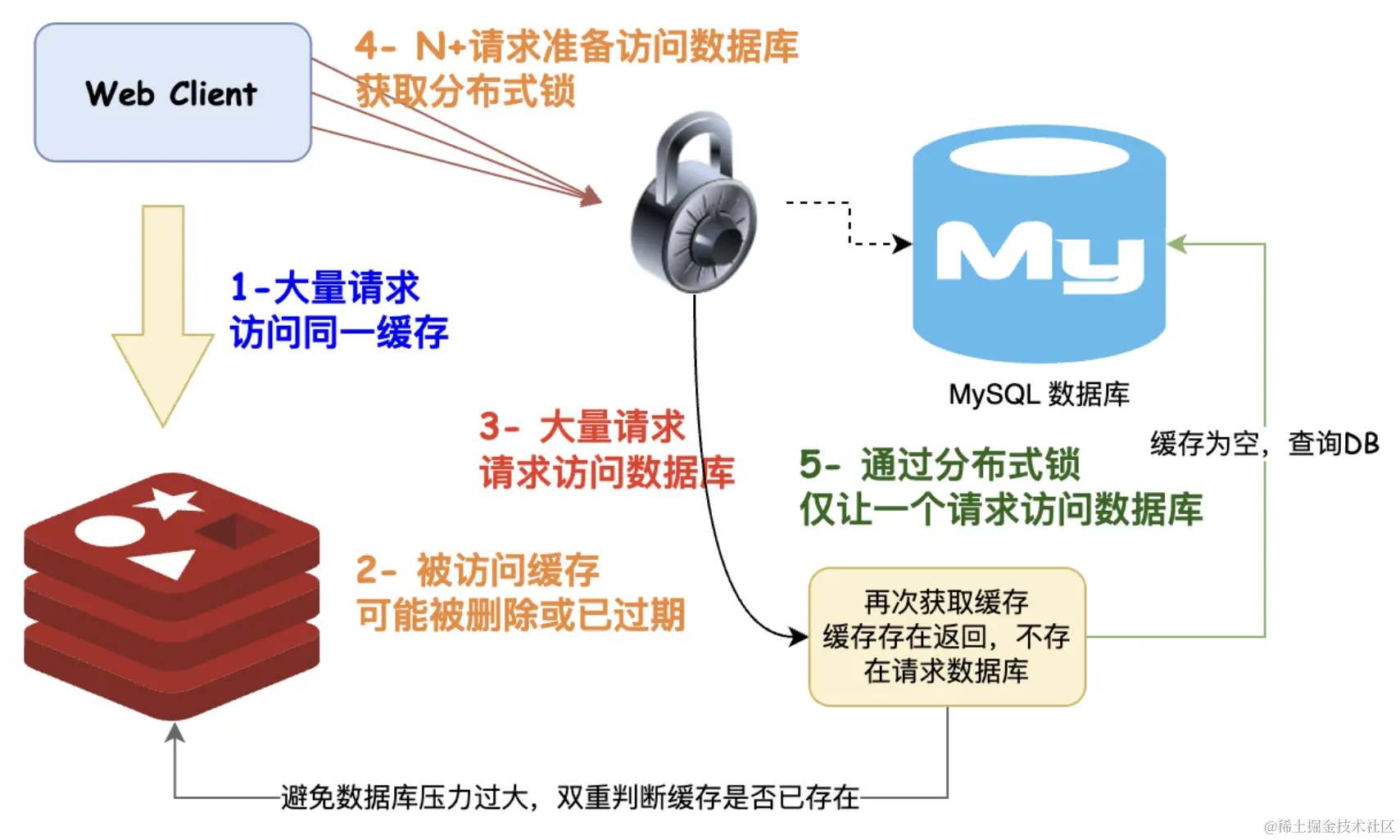
缓存击穿只会逻辑过期 OR 互斥锁?深入思考 == 鹤立鸡群
网上但凡看得见的文章,大部分在说缓存穿透时都是无脑分布式锁 / 逻辑过期,分布式锁一点问题都没有么?逻辑过期一点问题都没有么?还能不能再进一步优化? 在聊聊缓存击穿的双重判定锁之前,我们将按照循循渐进…...

从 Seq2Seq 到 Attention:彻底改变序列建模
探究Attention机制和意力的起源。 简介 在这篇博文[1]中,将讨论注意力机制的起源,然后介绍第一篇将注意力用于神经机器翻译的论文。由于上下文压缩、短期记忆限制和偏差,具有 2 个 RNN 的 Seq2Seq 模型失败了。该模型的 BLEU 分数随着序列长度…...

手机通讯类、ip查询、智能核验、生活常用API接口推荐
手机通讯类 手机号码归属地:提供三大运营商的手机号码归属地查询。 空号检测:通过手机号码查询其在网活跃度,返回包括空号、停机等状态。 手机在网状态:支持传入三大运营商的号码,查询手机号在网状态,返…...

1.6 基本安全设计准则
思维导图: 1.6 基本安全设计准则笔记 目标:理解和遵循一套广泛认可的安全设计准则,以指导保护机制的开发。 主要准则: 机制的经济性:安全机制应设计得简单、短小,便于测试和验证,减少漏洞和降…...

图扑 HT for Web 手机端运维管理系统
随着信息技术的快速发展,网络技术的应用涉及到人们生活的方方面面。其中,手机运维管理系统可提供数字化、智能化的方式,帮助企业和组织管理监控企业的 IT 环境,提高运维效率、降低维护成本、增强安全性、提升服务质量,…...
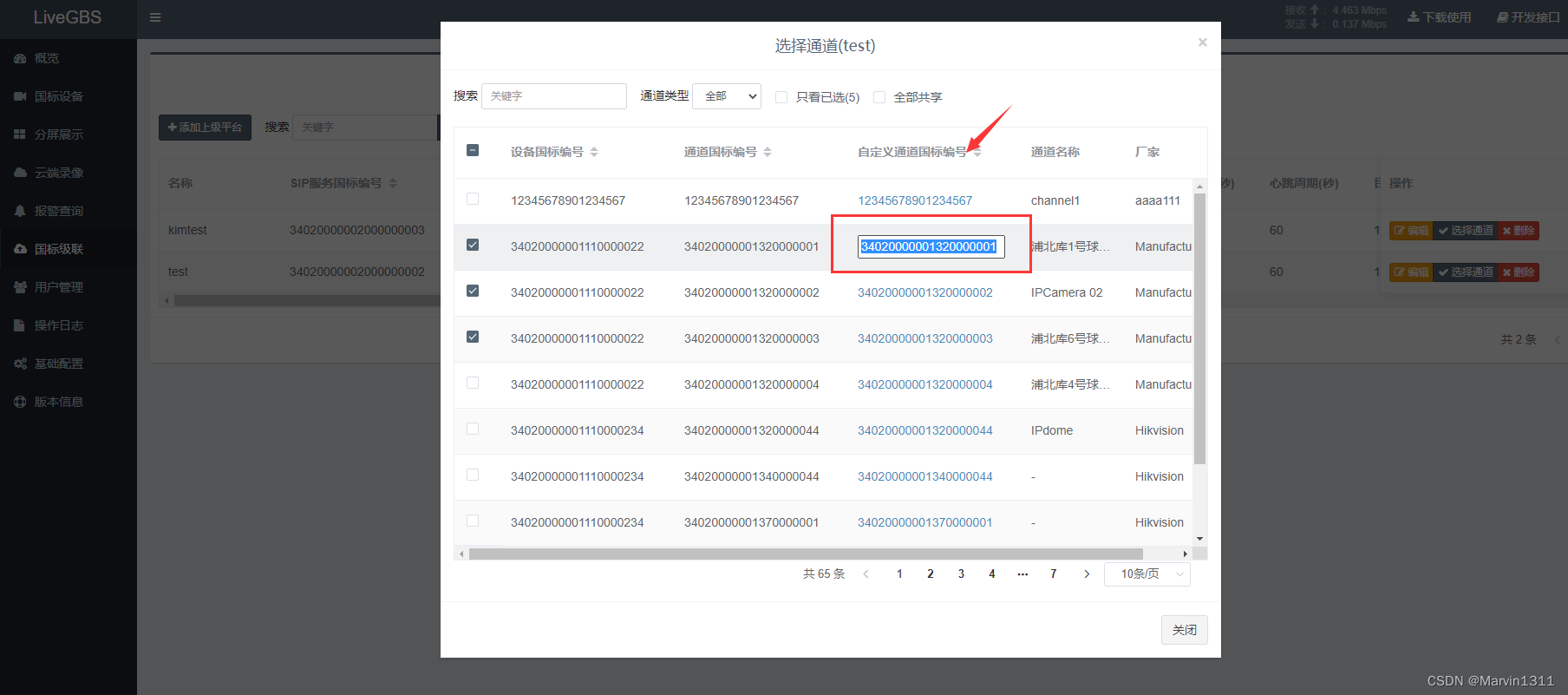
LiveGBS流媒体平台GB/T28181常见问题-国标级联海康国标级联大华国标级联华为等,配置了国标级联, 上级看不到通道该怎么办?
LiveGBS常见问题-国标级联海康国标级联大华国标级联华为等,配置了国标级联, 上级看不到通道该怎么办? 1、如何配置国标级联2、上级看不到通道排查2.1、是否共享通道2.3、通道编号是否满足上级要求 3、如何抓包分析4、搭建GB28181视频直播平台 1、如何配置国标级联 …...
数字频带传输——二进制数字调制及MATLAB仿真
文章目录 前言一、OOK1、表达式2、功率谱密度3、调制框图 二、2PSK1、表达式2、功率谱密度 三、2FSK1、表达式 四、MATLAB 仿真1、MATLAB 源码2、仿真及结果①、输入信号及频谱图②、2ASK 调制③、2PSK 调制④、2FSK 调制⑤、随机相位 2FSK 调制 五、资源自取 前言 数字频带信…...

Bitdu 150万美元投资MSG:Web3合作典范催动极致交易体验
在Web3时代,如何一键把握DEX领域的机遇,是摆在一众中心化交易所面前的难题。 近期,新锐加密资产交易所Bitdu向MsgSender(MSG)投资150万美元,引起了专业的交易者们的关注。大家普遍认为,这一事件…...

CentOS一键部署Docker
Docker官网:https://www.docker.com/ CentOS(7.6) Docker(18.06.1)一键安装脚本 #!/bin/bash echo "1、安装依赖..." yum -y install gcc yum -y install gcc-c##验证gcc版本 gcc -vecho "2、卸载老…...
Centos虚拟机安装配置与MobaXterm工具及Linux常用命令
目录 一、Centos操作系统 1.1 Centos介绍 1.2 Centos虚拟机安装 1.3 配置centos的镜像 1.4 虚拟机开机初始设置 1.4.1 查看网络配置 1.4.2 编辑网络配置 二、MobaXterm工具 2.1 MobaXterm介绍 2.2 MobaXterm安装 2.3 切换国内源 三、Linux常用命令和模式 3.1 查看网络配置 …...
springboot医院绩效考核系统源码
医院绩效考核系统是一种以人力资源管理为基础,选用适合医院组织机构属性的绩效理论和方法,基于医院战略目标,构建全方位的绩效考评体系,在科学、合理的绩效管理体系基础上,采用科学管理的方法,如平衡计分卡…...

Java--枚举类型
Java中枚举类型可以取代一般的常量定义方式,可以将常量封装在类或接口中;枚举类型本质上还是以类的形式存在的,枚举类型继承于java.lang.Enum类,定义一个枚举类型时,每一个枚举类型成员都可以看做是枚举类型的一个实例…...
有没有好用的配音工具?推荐这5款
为什么越来越多的短视频创作者愿意使用配音工具。 除了这些配音工具可以进行批量处理,实现大规模的音频制作,从而提高生产效率。还可以帮助其节约大量的人力,想一下,以前配音,不同的音色、角色需要不同的人来完成&…...

tomcat安装及配置教程
以下是 Tomcat 安装及配置的基本步骤: 下载 Tomcat 并解压缩:在 Apache Tomcat 的官网上下载最新版本的 Tomcat,然后解压缩到你想要安装的目录下(比如 /usr/local/tomcat)。 配置 PATH 环境变量:在终端中打…...

UNIPOSE: DETECTING ANY KEYPOINTS(2023.10.12)
文章目录 AbstractIntroduction现有的方法存在哪些不足基于此,我们提出了哒哒哒取得惊人的成绩Related Work MethodMULTI -MODALITY PROMPTS ENCODING(多模态提示编码)Textual Prompt Encoder(文本提示编码器)Visual P…...
如何用ChatGPT快速写出一份合格的PPT报告
我们【AI写稿专家】的小伙伴中有很多企业高管和公务员,大家经常有写报告写ppt的需求,下面小编给大家介绍一下我们新发布生成PPT的功能,很简单很方便,看完大家不到1分钟就能生成一份拿得出手的PPT报告,再也不用费尽心思…...
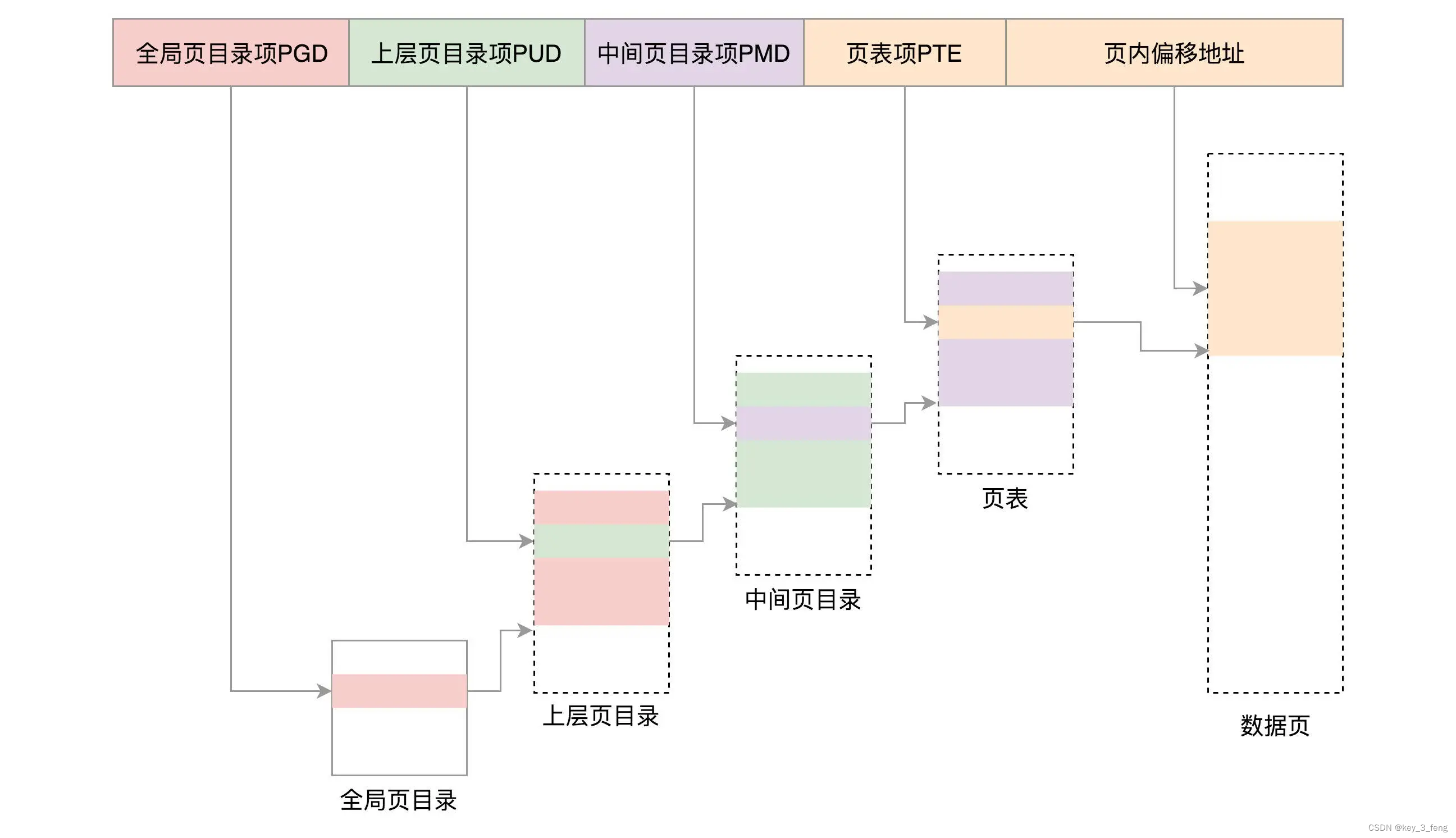
Linux内存管理的分页机制
分段机制的原理如下: 分段机制下的虚拟地址由两部分组成,段选择子和段内偏移量。段选择子就保存在段寄存器里面。段选择子里面最重要的是段号,用作段表的索引。段表里面保存的是这个段的基地址、段的界限和特权等级等。虚拟地址中的段内偏移量…...

Unity DOTS系列之托管/非托管Component的区别与性能分析
最近DOTS发布了正式的版本, 我们来分享一下DOTS里面托管与非托管Component的区别与性能分析,方便大家上手学习掌握Unity DOTS开发。托管与非托管的区别在于是不是基于自动垃圾回收的。托管是由垃圾回收器来负责自动回收,非托管需要我们手动来做相关内存管…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
