数字频带传输——二进制数字调制及MATLAB仿真
文章目录
- 前言
- 一、OOK
- 1、表达式
- 2、功率谱密度
- 3、调制框图
- 二、2PSK
- 1、表达式
- 2、功率谱密度
- 三、2FSK
- 1、表达式
- 四、MATLAB 仿真
- 1、MATLAB 源码
- 2、仿真及结果
- ①、输入信号及频谱图
- ②、2ASK 调制
- ③、2PSK 调制
- ④、2FSK 调制
- ⑤、随机相位 2FSK 调制
- 五、资源自取
前言
数字频带信号通常也称为数字调制信号,其信号频谱通常是带通型的,适合于在带通型信道中传输。数字调制是将基带数字信号变换成适合带通型信道传输的一种信号处理方式,正如模拟通信中的一样,可以通过对基带信号的频谱搬移来适应信道特性,也到同样的目的可以采用频率调制、相位调制的方式来达到同样的目的。
本文将主要通过 Matlab 来学习二进制的调制解调方式,包括 OOK、2PSK、2FSK,并分析和仿真这些调制系统。
一、OOK
1、表达式
如果将二进制码元 “0” 对应信号 0,“1” 对应信号 A c o s 2 π f c t Acos2\pi f_ct Acos2πfct,则 OOK 信号可以写成如下表达式:
s ( t ) = ∑ n a n g ( t − n T s ) A c o s 2 π f c t s(t)={\sum_na_ng(t-nT_s)}Acos2\pi f_ct s(t)=n∑ang(t−nTs)Acos2πfct
其中, a n ∈ a_n\in an∈ {0,1}, g ( t ) = { 1 0 ≤ t ≤ T s 0 其他 g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases} g(t)={100≤t≤Ts其他
可以看到,上式是数字基带信号 m ( t ) = ∑ n a n g ( t − n T s ) m(t)=\sum_na_ng(t-nT_s) m(t)=∑nang(t−nTs) 经过 DSB 调制后形成的信号,OOK 信号波形如下图所示:
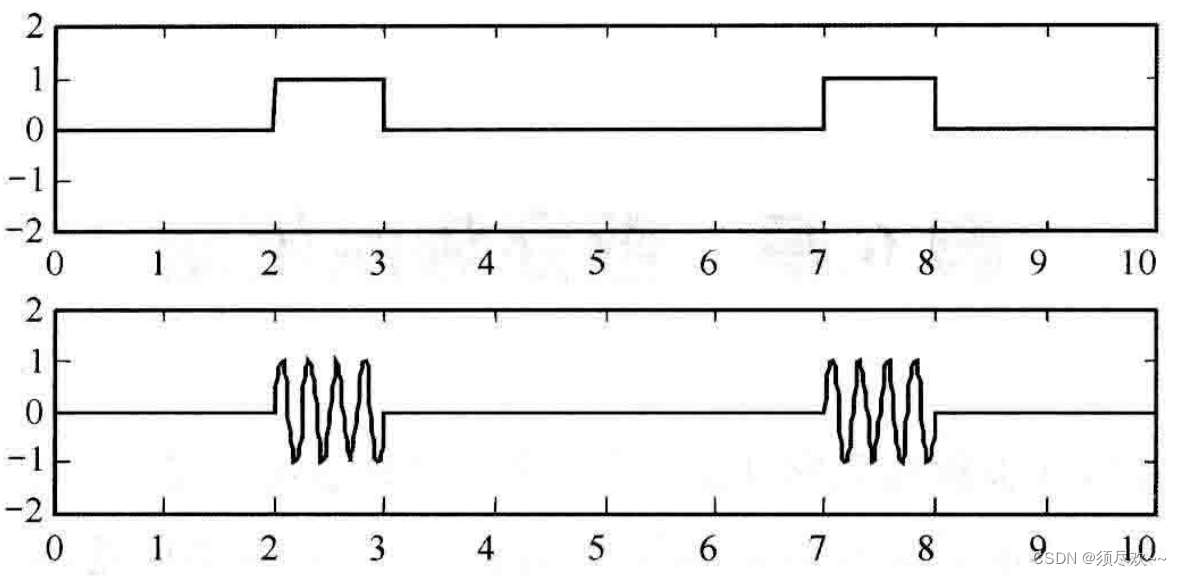
2、功率谱密度
OOK 信号的功率谱密度为:
P s ( f ) = A 2 4 [ P m ( f − f c ) + P m ( f + f c ) ] P_s(f)=\frac{A^2}{4}[P_m(f-f_c)+P_m(f+f_c)] Ps(f)=4A2[Pm(f−fc)+Pm(f+fc)]
3、调制框图
OOK 的调制框图如下图所示:
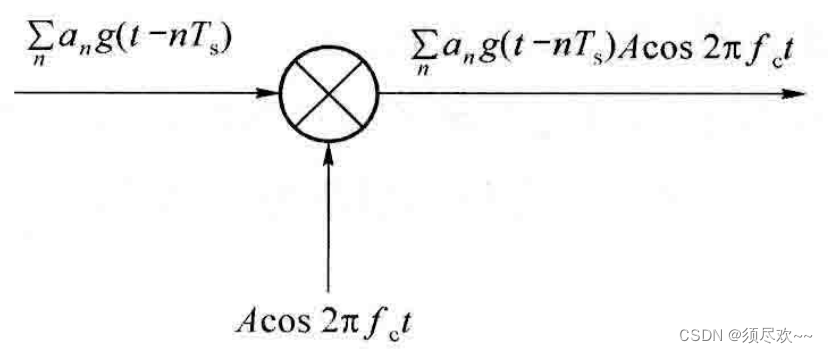
二、2PSK
1、表达式
将二进制码元 “0” 对应相位为 π \pi π 的载波 − A c o s 2 π f c t -Acos2\pi f_ct −Acos2πfct,“1” 对应相位为 0 的载波 A c o s 2 π f c t Acos2 \pi f_ct Acos2πfct,则 2PSK 信号可以写成如下表达式:
s ( t ) = ∑ n a n g ( t − n T s ) A c o s 2 π f c t s(t)={\sum_na_ng(t-nT_s)}Acos2\pi f_ct s(t)=n∑ang(t−nTs)Acos2πfct
其中, a n ∈ a_n\in an∈ {+1,-1}, g ( t ) = { 1 0 ≤ t ≤ T s 0 其他 g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases} g(t)={100≤t≤Ts其他
2PSK 信号波形如下图所示,其实现框图与 OOK 相同,只是输入是双极性的
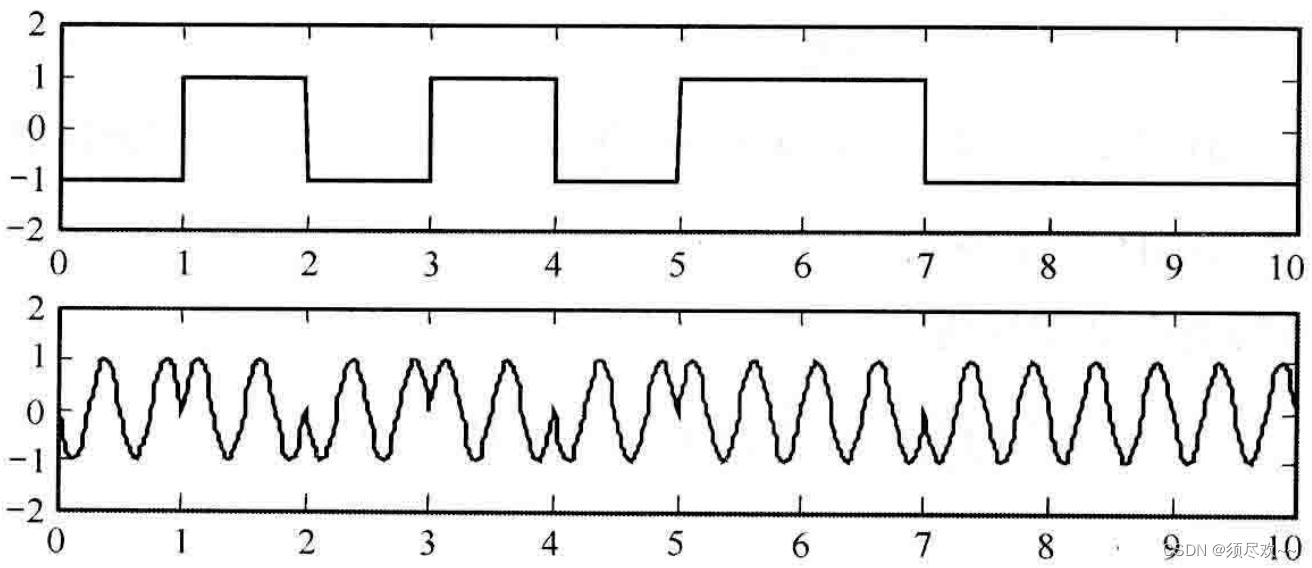
2、功率谱密度
2PSK 信号的功率谱密度为:
P s ( f ) = A 2 4 [ P m ( f − f c ) + P m ( f + f c ) ] P_s(f)=\frac{A^2}{4}[P_m(f-f_c)+P_m(f+f_c)] Ps(f)=4A2[Pm(f−fc)+Pm(f+fc)]
三、2FSK
1、表达式
将二进制码元 “0” 对应载波 A c o s 2 π f 1 t Acos2 \pi f_1t Acos2πf1t,“1” 对应载波 A c o s 2 π f 2 t Acos2\pi f_2t Acos2πf2t,则形成 2FSK 信号,可以写成如下表达式:
s ( t ) = ∑ n a n ‾ g ( t − n T s ) A c o s ( 2 π f 1 t + φ n ) + ∑ n a n g ( t − n T s ) A c o s ( 2 π f 1 t + θ n ) s(t)=\sum_n \overline{a_n}g(t-nT_s)Acos(2\pi f_1t+\varphi_n)+\sum_n a_ng(t-nT_s)Acos(2\pi f_1t+\theta_n) s(t)=n∑ang(t−nTs)Acos(2πf1t+φn)+n∑ang(t−nTs)Acos(2πf1t+θn)
当 a n = 1 a_n=1 an=1 时,对应的传输信号频率为 f 2 f_2 f2,当 a n = 0 a_n=0 an=0 时,对应的传输信号频率为 f 1 f_1 f1,上式中, φ n \varphi_n φn、 θ n \theta_n θn 时两个频率波的初相。2FSK 也可以写成另外的形式如下:
s ( t ) = A c o s [ 2 π f c t + 2 π h ∑ n = − ∞ ∞ a n g ( t − n T s ) ] s(t)=Acos[2\pi f_ct+2\pi h\sum_{n=-\infty}^{\infty}{a_n}g(t-nT_s)] s(t)=Acos[2πfct+2πhn=−∞∑∞ang(t−nTs)]
其中, a n ∈ a_n\in an∈ {+1,-1}, f c = ( f 1 + f 2 ) / 2 f_c=(f_1+f_2)/2 fc=(f1+f2)/2, g ( t ) = { 1 0 ≤ t ≤ T s 0 其他 g(t)=\begin{cases} 1& 0\le t \le T_s \\ 0& \text{其他} \end{cases} g(t)={100≤t≤Ts其他, h = ∣ f c − f 1 ∣ h=|f_c-f_1| h=∣fc−f1∣ 为频偏,其波形如下图所示:
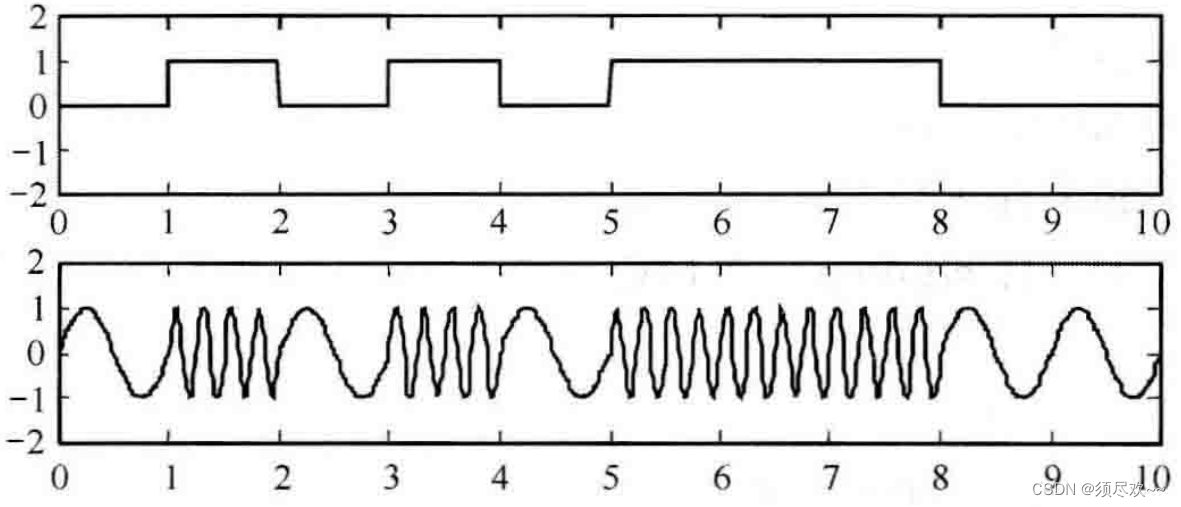
2FSK 信号可以看成是两个不同载波的 OOK 信号的叠加:
s ( t ) = s 1 ( t ) c o s ( ω t + ϕ 1 ) + s 2 ( t ) c o s ( ω t + ϕ 2 ) s(t)=s_1(t)cos(\omega t+\phi_1)+s_2(t)cos(\omega_t+\phi_2) s(t)=s1(t)cos(ωt+ϕ1)+s2(t)cos(ωt+ϕ2)
当这两项不相关时(如载波之间频率差足够大),它的功率谱密度为:
P s = 1 4 [ P s 1 ( f + f 1 ) + P s 1 ( f − f 1 ) ] + 1 4 [ P s 2 ( f + f 1 ) + P s 1 ( f − f 2 ) ] P_s=\frac{1}{4}[P_{s1}(f+f_1)+P_{s1}(f-f_1)]+\frac{1}{4}[P_{s2}(f+f_1)+P_{s1}(f-f_2)] Ps=41[Ps1(f+f1)+Ps1(f−f1)]+41[Ps2(f+f1)+Ps1(f−f2)]
四、MATLAB 仿真
以下代码使用 MATLAB 产生独立等概的二进制信源,并完成了下面三个功能:
- 画出 OOK 信号波形及其功率谱;
- 画出 2PSK 信号波形及其功率谱;
- 画出 2FSK 信号波形及其功率谱(设 ∣ f 1 − f 2 ∣ > > 1 T s |f_1-f_2|>>\frac{1}{T_s} ∣f1−f2∣>>Ts1)。
1、MATLAB 源码
% 2ASK,2PSK
clear all;
close all;A = 1;
fc = 2; % 2Hz;
N_sample = 8;
N = 500; % 码元数
Ts = 1; % 1 baud/sdt = Ts/fc/N_sample; % 波形采样间隔
t = 0 : dt : N*Ts-dt;
T = dt * length(t);
Lt = length(t);% 产生二进制信源
d = sign(randn(1, N));
dd = sigexpand((d+1)/2, fc*N_sample);
gt = ones(1, fc*N_sample); % NRZ 波形figure(1)
subplot(221); % 输入 NRZ 信号波形(单极性)
d_NRZ = conv(dd, gt);
plot(t, d_NRZ(1:length(t)));
axis([0 10 0 1.2]); xlabel('t/s'); ylabel('输入信号');subplot(222); % 输入 NRZ 频谱
[f, d_NRZf] = T2F(t, d_NRZ(1:length(t)));
plot(f, 10*log10(abs(d_NRZf).^2/T));
axis([-2 2 -50 10]); xlabel('f/Hz'); ylabel('输入信号功率谱密度(dB/Hz)');%2ASK信号
ht = A*cos(2*pi*fc*t);
s_2ask = d_NRZ(1:Lt).*ht;subplot(223)
plot(t,s_2ask);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('2ASK');[f, s_2askf]=T2F(t, s_2ask );
subplot(224)
plot(f, 10*log10(abs(s_2askf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2ASK功率谱密度(dB/Hz)');figure(2)
%2PSK信号
d_2psk = 2*d_NRZ-1;
s_2psk = d_2psk(1:Lt).*ht;
subplot(221)
plot(t,s_2psk);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('2PSK');subplot(222)
[f, s_2pskf] = T2F(t, s_2psk);
plot( f, 10*log10(abs(s_2pskf).^2/T) );
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2PSK功率谱密度(dB/Hz)');% 2FSK
% s_2fsk = Acos(2*pi*fc*t + int(2*d_NRZ-1) );sd_2fsk = 2*d_NRZ-1;s_2fsk = A*cos(2*pi*fc*t + 2*pi*sd_2fsk(1:length(t)).*t );
subplot(223)
plot(t, s_2fsk);
axis([0 10 -1.2 1.2]);xlabel('t/s'); ylabel('2FSK')
subplot(224)
[f, s_2fskf] = T2F(t, s_2fsk);
plot(f, 10*log10(abs(s_2fskf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('2FSK功率谱密度(dB/Hz)');% 随机相位 2FSK
fai = 2*pi*rand(1, N);
fai_2fsk = sigexpand(fai, fc*N_sample);
fai_2fsk = conv(fai_2fsk, gt);
s_2fskd = A*cos(2*pi*fc*t + 2*pi*sd_2fsk(1:length(t)).*t + fai_2fsk(1:length(t)) );
figure(3)
subplot(211);
plot(t, s_2fskd);
axis([0 10 -1.2 1.2]); xlabel('t/s'); ylabel('随机相位 2FSK');
[f, s_2fskdf] = T2F(t, s_2fskd);
subplot(212);
plot(f, 10*log10(abs(s_2fskdf).^2/T));
axis([-fc-4 fc+4 -50 10]); xlabel('f/Hz'); ylabel('随机相位 2FSK 功率谱密度(dB/Hz)');
2、仿真及结果
①、输入信号及频谱图
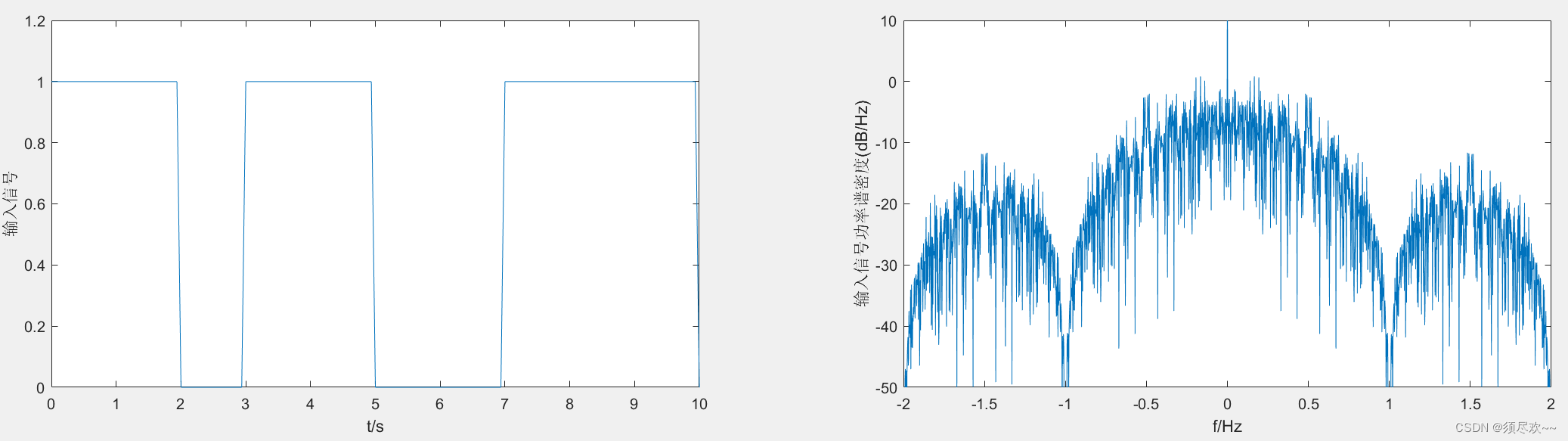
②、2ASK 调制
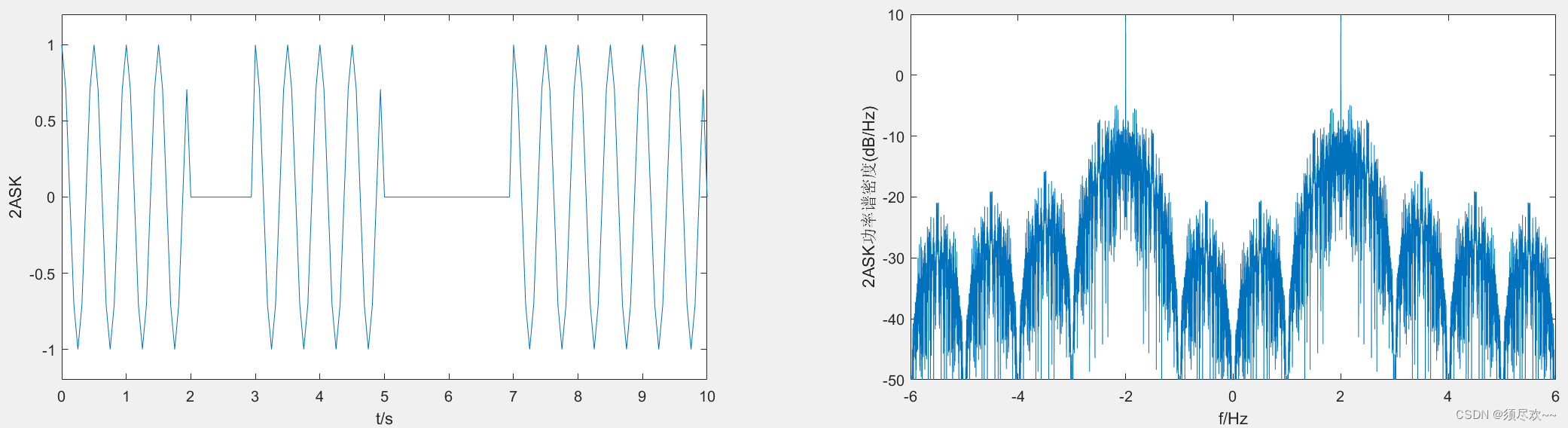
③、2PSK 调制
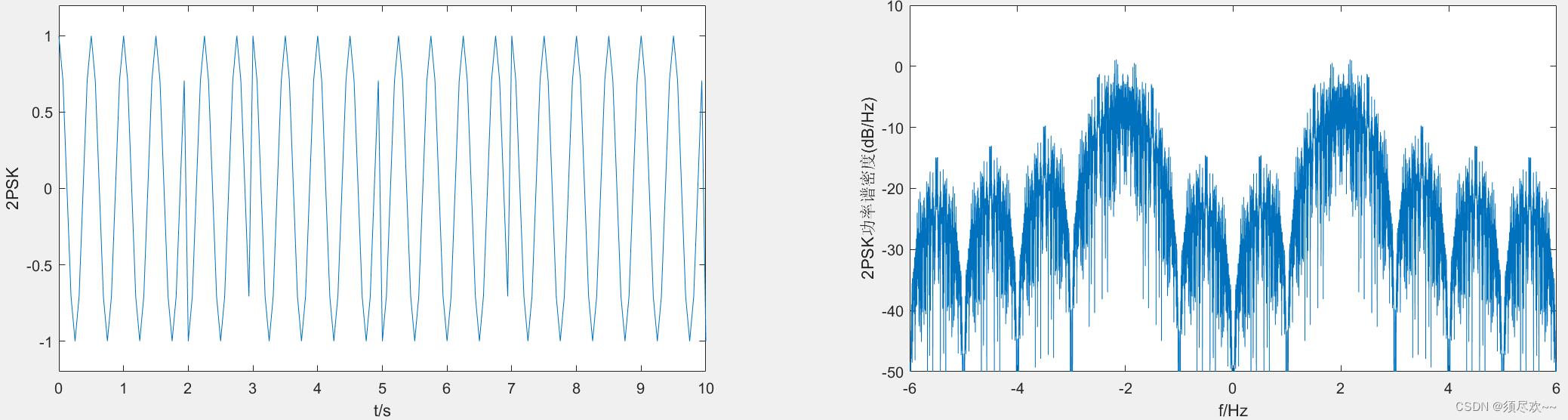
④、2FSK 调制
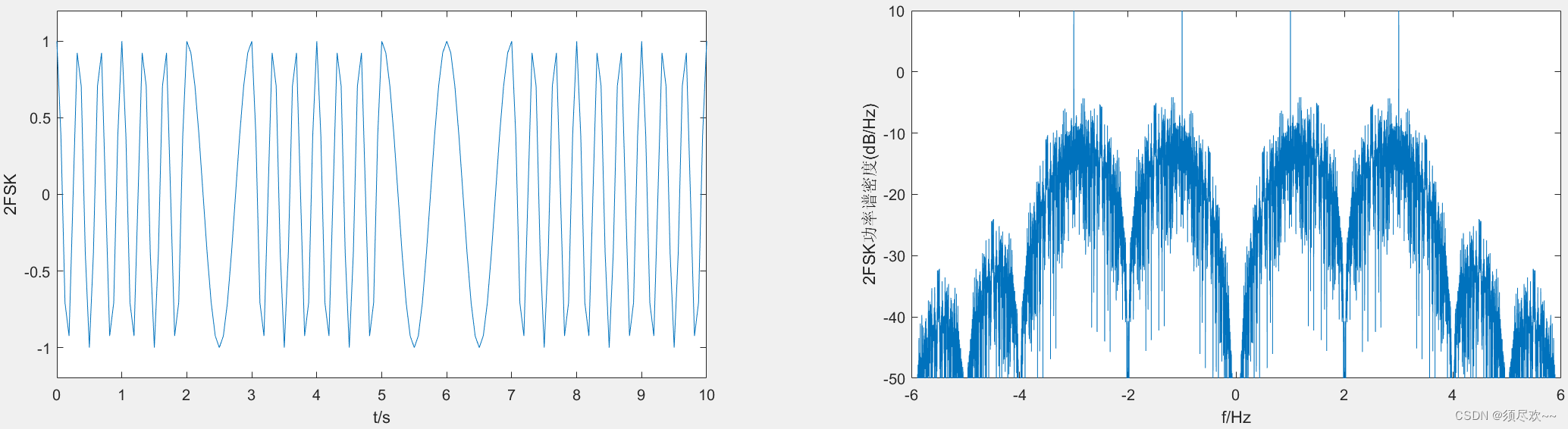
⑤、随机相位 2FSK 调制
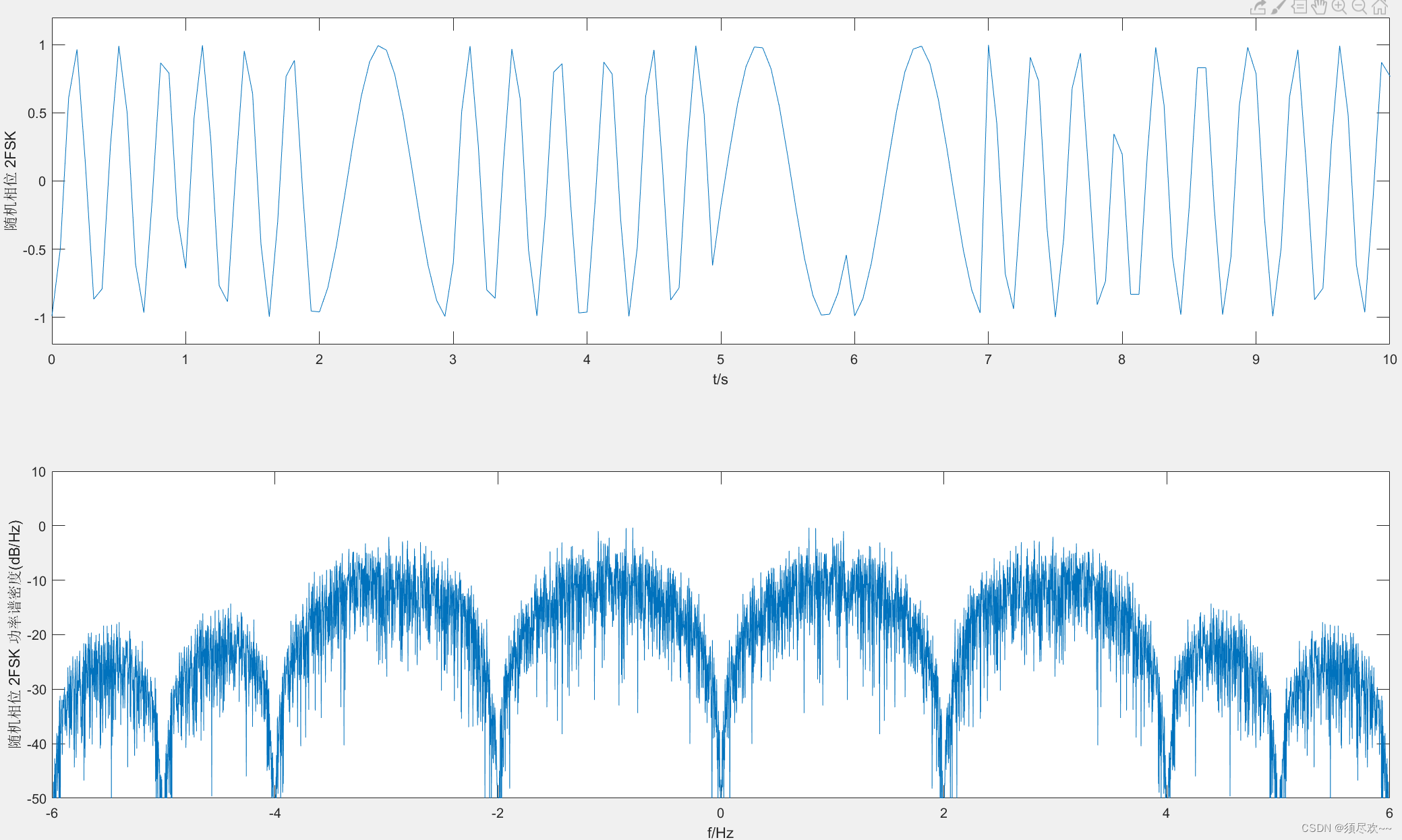
五、资源自取
二进制数字调制及MATLAB仿真
我的qq:2442391036,欢迎交流!
相关文章:

数字频带传输——二进制数字调制及MATLAB仿真
文章目录 前言一、OOK1、表达式2、功率谱密度3、调制框图 二、2PSK1、表达式2、功率谱密度 三、2FSK1、表达式 四、MATLAB 仿真1、MATLAB 源码2、仿真及结果①、输入信号及频谱图②、2ASK 调制③、2PSK 调制④、2FSK 调制⑤、随机相位 2FSK 调制 五、资源自取 前言 数字频带信…...

Bitdu 150万美元投资MSG:Web3合作典范催动极致交易体验
在Web3时代,如何一键把握DEX领域的机遇,是摆在一众中心化交易所面前的难题。 近期,新锐加密资产交易所Bitdu向MsgSender(MSG)投资150万美元,引起了专业的交易者们的关注。大家普遍认为,这一事件…...

CentOS一键部署Docker
Docker官网:https://www.docker.com/ CentOS(7.6) Docker(18.06.1)一键安装脚本 #!/bin/bash echo "1、安装依赖..." yum -y install gcc yum -y install gcc-c##验证gcc版本 gcc -vecho "2、卸载老…...
Centos虚拟机安装配置与MobaXterm工具及Linux常用命令
目录 一、Centos操作系统 1.1 Centos介绍 1.2 Centos虚拟机安装 1.3 配置centos的镜像 1.4 虚拟机开机初始设置 1.4.1 查看网络配置 1.4.2 编辑网络配置 二、MobaXterm工具 2.1 MobaXterm介绍 2.2 MobaXterm安装 2.3 切换国内源 三、Linux常用命令和模式 3.1 查看网络配置 …...
springboot医院绩效考核系统源码
医院绩效考核系统是一种以人力资源管理为基础,选用适合医院组织机构属性的绩效理论和方法,基于医院战略目标,构建全方位的绩效考评体系,在科学、合理的绩效管理体系基础上,采用科学管理的方法,如平衡计分卡…...

Java--枚举类型
Java中枚举类型可以取代一般的常量定义方式,可以将常量封装在类或接口中;枚举类型本质上还是以类的形式存在的,枚举类型继承于java.lang.Enum类,定义一个枚举类型时,每一个枚举类型成员都可以看做是枚举类型的一个实例…...
有没有好用的配音工具?推荐这5款
为什么越来越多的短视频创作者愿意使用配音工具。 除了这些配音工具可以进行批量处理,实现大规模的音频制作,从而提高生产效率。还可以帮助其节约大量的人力,想一下,以前配音,不同的音色、角色需要不同的人来完成&…...

tomcat安装及配置教程
以下是 Tomcat 安装及配置的基本步骤: 下载 Tomcat 并解压缩:在 Apache Tomcat 的官网上下载最新版本的 Tomcat,然后解压缩到你想要安装的目录下(比如 /usr/local/tomcat)。 配置 PATH 环境变量:在终端中打…...

UNIPOSE: DETECTING ANY KEYPOINTS(2023.10.12)
文章目录 AbstractIntroduction现有的方法存在哪些不足基于此,我们提出了哒哒哒取得惊人的成绩Related Work MethodMULTI -MODALITY PROMPTS ENCODING(多模态提示编码)Textual Prompt Encoder(文本提示编码器)Visual P…...
如何用ChatGPT快速写出一份合格的PPT报告
我们【AI写稿专家】的小伙伴中有很多企业高管和公务员,大家经常有写报告写ppt的需求,下面小编给大家介绍一下我们新发布生成PPT的功能,很简单很方便,看完大家不到1分钟就能生成一份拿得出手的PPT报告,再也不用费尽心思…...
Linux内存管理的分页机制
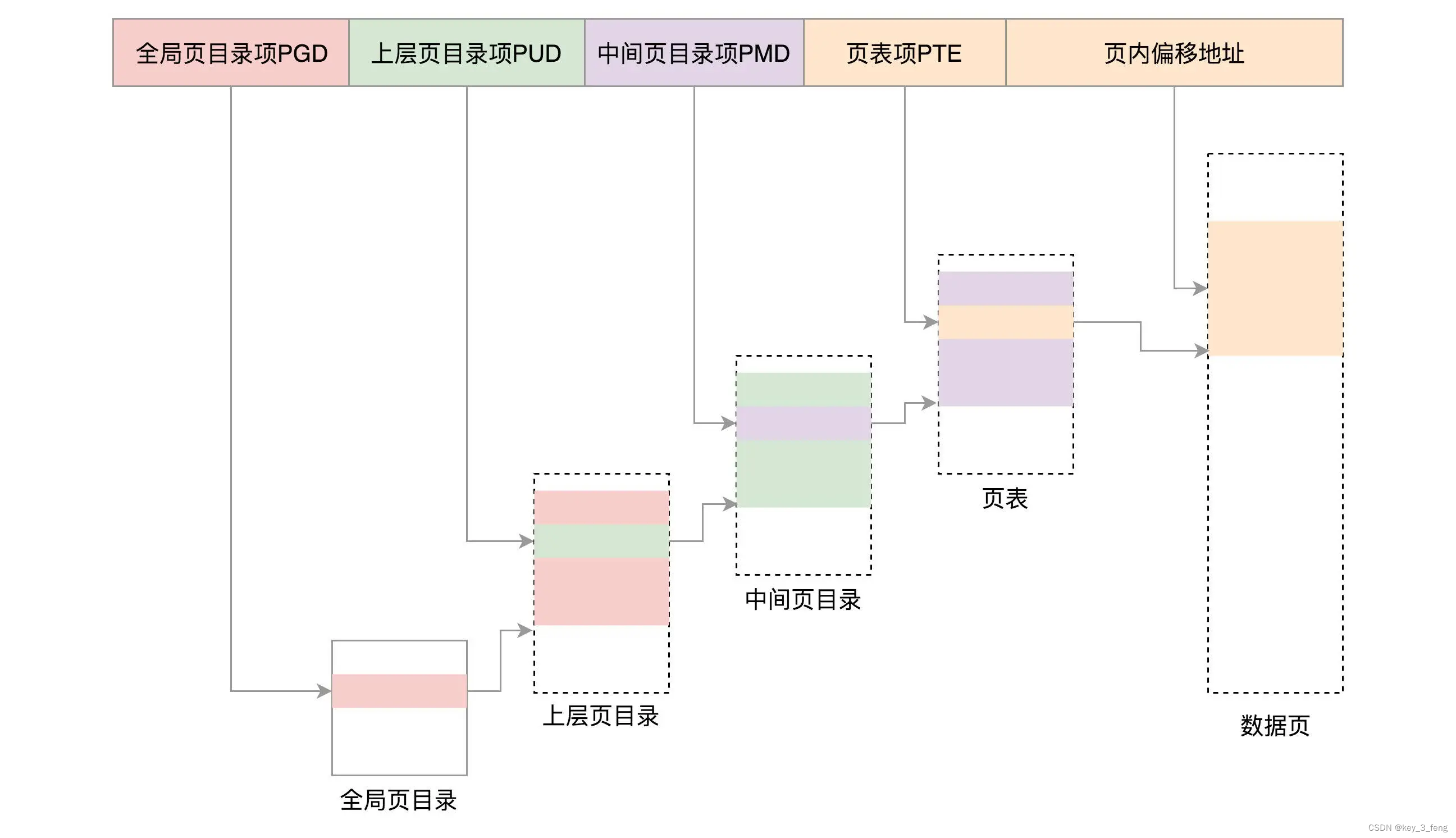
分段机制的原理如下: 分段机制下的虚拟地址由两部分组成,段选择子和段内偏移量。段选择子就保存在段寄存器里面。段选择子里面最重要的是段号,用作段表的索引。段表里面保存的是这个段的基地址、段的界限和特权等级等。虚拟地址中的段内偏移量…...

Unity DOTS系列之托管/非托管Component的区别与性能分析
最近DOTS发布了正式的版本, 我们来分享一下DOTS里面托管与非托管Component的区别与性能分析,方便大家上手学习掌握Unity DOTS开发。托管与非托管的区别在于是不是基于自动垃圾回收的。托管是由垃圾回收器来负责自动回收,非托管需要我们手动来做相关内存管…...

elementui el-upload 上传文件
文章目录 前言一、Html2.上传 总结 前言 在使用element中的el-upload上传文件或者图片时,需要先把el-upload的自动上传改为手动上传:auto-upload“false”然后el-upload内部会调用this.$refs.upload.submit();方法,从而实现多个文件上传。 提示…...

Python图像处理【15】基于非锐化掩码锐化图像
基于非锐化掩码锐化图像 0. 前言1. 使用 scikit-image filters 模块执行非锐化掩码2. 使用 PIL ImageFilter 模块执行非锐化掩码3. 使用 SimpleITK 执行拉普拉斯锐化4. 使用 OpenCV 实现非锐化掩码小结系列链接 0. 前言 非锐化滤波器是一个简单的锐化算子,通过从原…...
介绍几款Linux 下终极SSH客户端
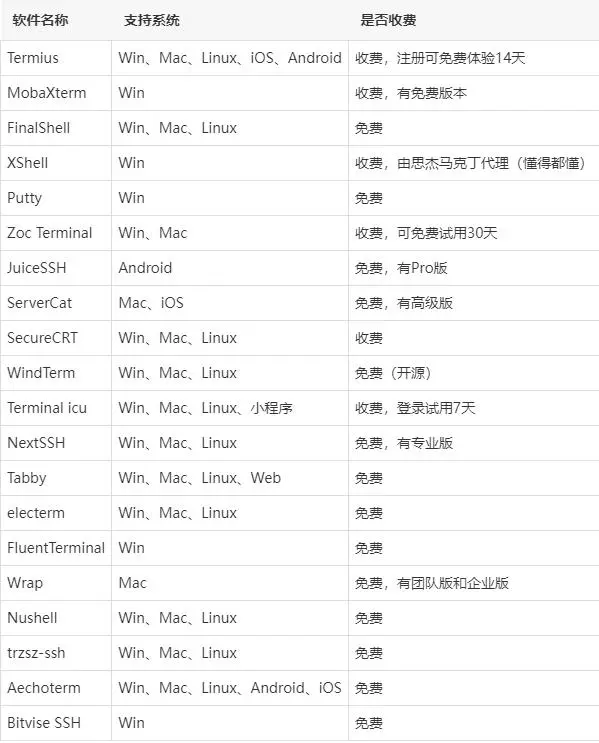
安全外壳协议(Secure Shell,简称 SSH)是一种网络连接协议,允许您通过网络远程控制计算机。特别是在Linux命令行模式下,使用SSH,可以很方便管理linux上的运维工作。以下是一些最受欢迎的Linux SSH客户端&…...
项目综合实训,vrrp+bfd,以及策略路由的应用
目录 一. 项目需求 二. Visio设备画图 三. 设备选型 三.vlan规划 四.Ip地址规划 五.实验拓扑图 六.配置过程及结果 项目需求 1.S1作为VLAN10的主网关和根桥,S2作为v…...
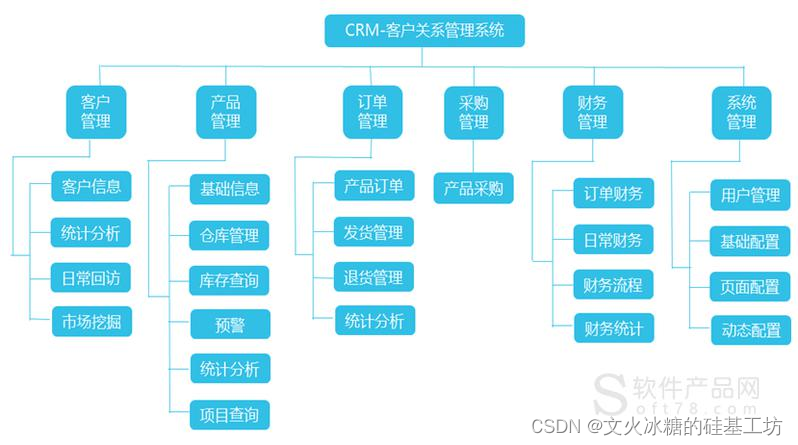
[架构之路-246/创业之路-77]:目标系统 - 纵向分层 - 企业信息化的呈现形态:常见企业信息化软件系统 - 客户关系管理系统CRM
目录 前言: 一、企业信息化的结果:常见企业信息化软件 1.1 客户关系管理系统CRM 1.1.1 什么是客户关系管理系统 1.1.2 CRM总体架构 1.1.3 什么类型的企业需要CRM 1.1.4 创业公司在什么阶段需要CRM 1.1.5 研发型创业公司什么时候需要CRM 1.1.6 C…...
python manage.py createsuperuser运行错误
我把思念作笺,随风而去,落在你常路过的那个街角… 错误复现 PS D:\教学文件\Django\djangoProject\webDemo02> python manage.py createsuperuser System check identified some issues:WARNINGS: ?: (urls.W005) URL namespace admin isnt unique…...

解决恶意IP地址攻击:保卫网络安全的有效方法
随着互联网的发展,网络安全威胁变得日益复杂,其中包括恶意IP地址攻击。这些攻击通常是网络犯罪分子的手段之一,用于入侵系统、窃取数据或进行其他恶意活动。本文将探讨如何解决恶意IP地址攻击,以保护网络安全。 恶意IP地址攻击是…...
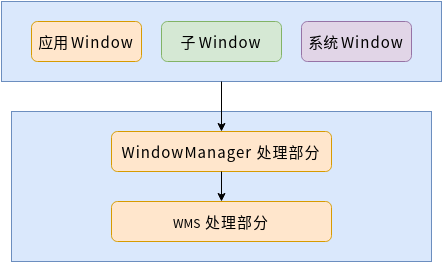
Android WMS——WMS窗口添加(十)
Android 的 WMS(Window Manager Service)是一个关键组件,负责管理窗口的创建、显示、布局和交互等。Window 的操作有两大部分,一部分是 WindowManager 来处理,一部分是 WMS 来处理,如下图所示: …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
