Acwing 蓝桥杯 第二章 二分与前缀和
今天来补一下之前没写的总结,题是写完了,但是总结没写
感觉没什么好总结的啊,就当打卡了
789. 数的范围 - AcWing题库

思路:
一眼二分,典中典
先排个序,再用lower_bound和upper_bound维护相同的数的左界和右界就好了
注意特判无解
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=1e5+10;
const int mxe=2e5+10;
using namespace std;int n,q,x;
int a[mxn];
bool check(int x){return x>=0&&x<=n-1;
}
void solve(){cin>>n>>q;for(int i=0;i<n;i++) cin>>a[i];while(q--){cin>>x;int pos1=lower_bound(a,a+n,x)-a;int pos2=upper_bound(a,a+n,x)-a-1;if((!check(pos1)||!check(pos2))||(pos1>pos2)) cout<<-1<<" "<<-1<<'\n';else cout<<pos1<<" "<<pos2<<'\n';}
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}790. 数的三次方根 - AcWing题库
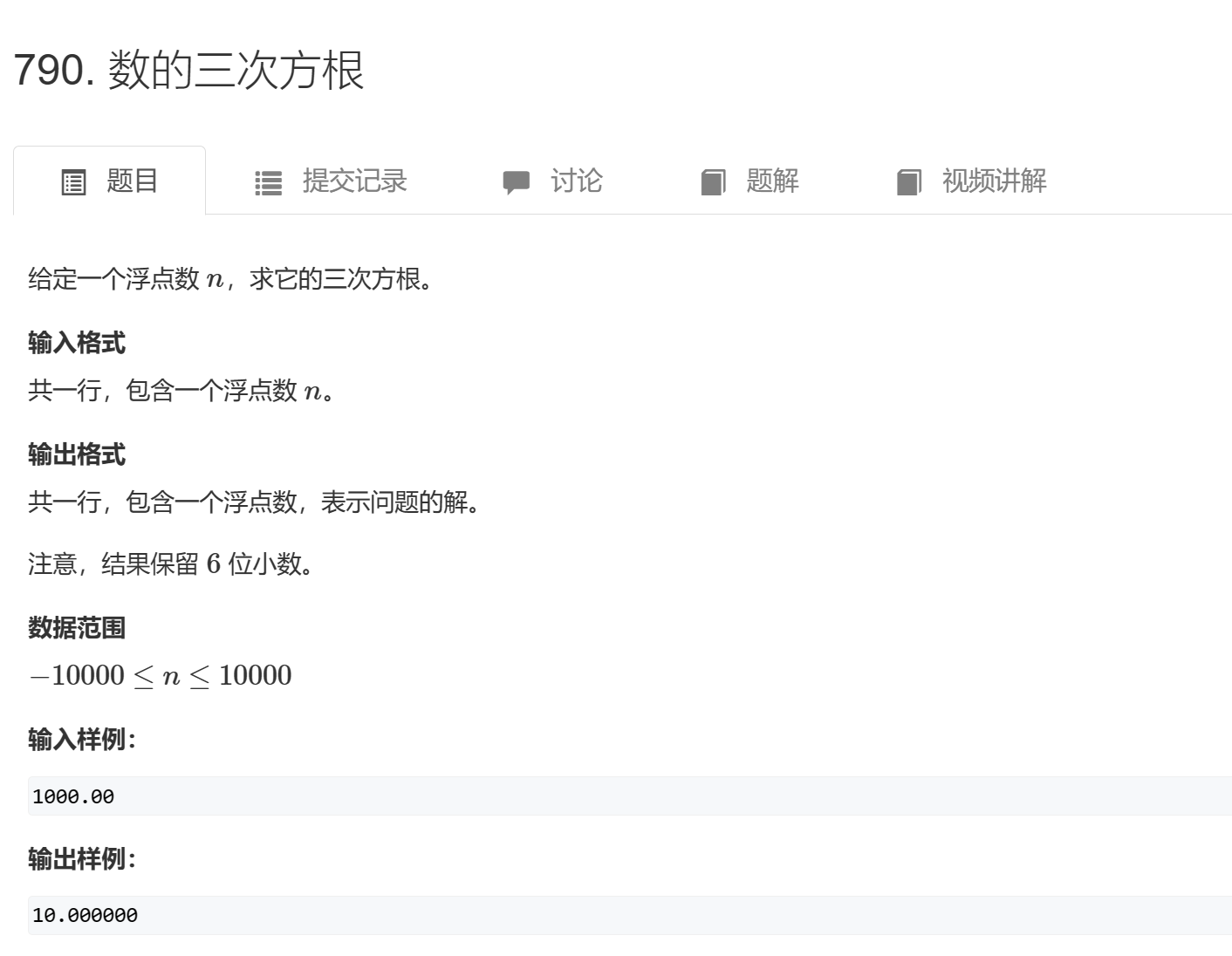
思路:
注意到答案具有单调性,因此二分即可
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=1e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;double n,ans;
bool check(double x){return x*x*x>=n;
}
void solve(){cin>>n;double l=-10000.0,r=10000.0;while(abs(r-l)>eps){double mid=(l+r)/2;if(check(mid)){ans=mid;r=mid;}else l=mid;}cout<<fixed<<setprecision(6)<<ans<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}AcWing 795. 前缀和 - AcWing

思路:
大一学弟也会写的前缀和板子
Code:
#include <bits/stdc++.h>
#define int long long
const int mxn=1e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;int n,m,l,r;
int a[mxn],sum[mxn];
void solve(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i];while(m--){cin>>l>>r;cout<<sum[r]-sum[l-1]<<"\n";}
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}796. 子矩阵的和 - AcWing题库

同样是大一学弟也会的二维前缀和,但是我可能不太会,嘻
Code:
#include <bits/stdc++.h>
#define int long long
#define y1 Y1
const int mxn=1e3+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;int n,m,q,x1,y1,x2,y2;
int a[mxn][mxn],sum[mxn][mxn];
void solve(){cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) cin>>a[i][j];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) sum[i][j]=sum[i-1][j]+sum[i][j-1]+a[i][j]-sum[i-1][j-1];}while(q--){cin>>x1>>y1>>x2>>y2;cout<<sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]<<'\n';}
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}730. 机器人跳跃问题 - AcWing题库

思路:
答案具有二分性,可以直接二分
然后在check函数里去模拟这个过程,如果中间存在能量值<0的情况就false,否则如果出现大于maxH的情况,那么剩下的只会得到,因此直接true就好了
Code:
#include <bits/stdc++.h>
#define int long long
#define y1 Y1
const int mxn=1e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;int n,mx=-1;
int h[mxn];
bool check(int x){int res=x;for(int i=0;i<=n;i++){if(h[i+1]>res){res-=(h[i+1]-res);}else{res+=(res-h[i+1]);}if(res>=mx) return true; if(res<0) return false;}return res>=0;
}
void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>h[i],mx=max(mx,h[i]);int l=0,r=1e5;int ans;while(l<=r){int mid=l+r>>1;if(check(mid)){ans=mid;r=mid-1;}else l=mid+1;}//check(19);cout<<ans<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}AcWing 1221. 四平方和 - AcWing

思路:
四指针枚举,想到先把两个指针的结果哈希一下,然后再去枚举两个指针,一个指针的复杂度是sqrt(n),两个就是O(n)的了
Code:
#include <bits/stdc++.h>
#define int long long
#define y1 Y1
const int mxn=2e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;map<int,pair<int,int> > v;
int n,len=0;
void solve(){cin>>n;for(int i=0;i*i<=n;i++){for(int j=0;i*i+j*j<=n;j++){v[i*i+j*j]={i,j};}}for(int i=0;i*i<=n;i++){for(int j=0;i*i+j*j<=n;j++){if(v.count(n-i*i-j*j)){cout<<i<<" "<<j<<" "<<v[n-i*i-j*j].second<<" "<<v[n-i*i-j*j].first<<'\n';return;}}}
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}1227. 分巧克力 - AcWing题库

思路:
直接去二分边长,然后去check函数计算能有多少巧克力块就行
Code:
#include <bits/stdc++.h>
#define int long long
#define y1 Y1
const int mxn=1e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;
struct ty{int h,w;
}p[mxn];int n,k;
bool check(int x){int res=0;for(int i=1;i<=n;i++){res+=(p[i].h/x)*(p[i].w/x);}return res>=k;
}
void solve(){cin>>n>>k;for(int i=1;i<=n;i++) cin>>p[i].h>>p[i].w;int l=1,r=1e5;int ans;while(l<=r){int mid=l+r>>1;if(check(mid)){ans=mid;l=mid+1;}else r=mid-1;}cout<<ans<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}99. 激光炸弹 - AcWing题库

思路:
数据范围都比较小,因此可以直接求个二维前缀和,然后求二维差分,维护最大值即可
#include <bits/stdc++.h>
//#define int long long
#define y1 Y1
const int mxn=5e3+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;int n,r,x,y,w;
int a[mxn][mxn];
void solve(){cin>>n>>r;r=min(r,5001);for(int i=1;i<=n;i++){cin>>x>>y>>w;x++,y++;a[x][y]+=w;}for(int i=1;i<=5001;i++){for(int j=1;j<=5001;j++) a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];}int ans=-1e9;for(int i=1;i+r-1<=5001;i++){for(int j=1;j+r-1<=5001;j++){int x1=i,y1=j;int x2=i,y2=j+r-1;int x3=i+r-1,y3=j;int x4=i+r-1,y4=j+r-1;int S=a[x4][y4]-a[x2-1][y2]-a[x3][y3-1]+a[x1-1][y1-1];ans=max(ans,S);}}cout<<ans<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}1230. K倍区间 - AcWing题库

思路:
很典,直接求前缀和,然后对前缀和取模k,两个模为0的点就可以作为k倍区间端点,然后用动态map维护即可,也可以算C(n,2)
Code:
#include <bits/stdc++.h>
#define int long long
#define y1 Y1
const int mxn=1e5+10;
const int mxe=2e5+10;
const double eps=1e-8;
using namespace std;map<int,int> mp;
int n,k;
int a[mxn],sum[mxn];
void solve(){cin>>n>>k;for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i],sum[i]%=k;int ans=0;for(int i=1;i<=n;i++){ans+=mp[sum[i]];mp[sum[i]]++;}cout<<ans+mp[0]<<'\n';
}
void init(){}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;init();while(__--)solve();return 0;
}相关文章:

Acwing 蓝桥杯 第二章 二分与前缀和
今天来补一下之前没写的总结,题是写完了,但是总结没写感觉没什么好总结的啊,就当打卡了789. 数的范围 - AcWing题库思路:一眼二分,典中典先排个序,再用lower_bound和upper_bound维护相同的数的左界和右界就…...

CSDN原力增长规则解读 实测一个月
CSDN原力越来越难了,当然,这对生态发展来说也是好事。介绍下原力增长有哪些渠道吧。发布原创文章:10分/次,每日上限为15分、2篇回答问题:1分/次,每日上限2分,2回答发动态:1分/次&…...
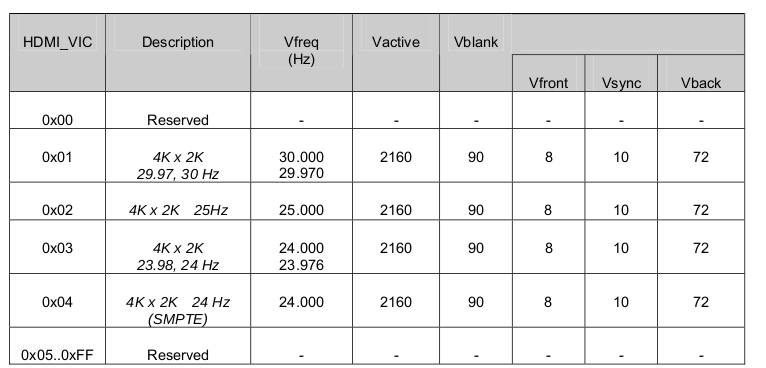
HDMI协议介绍(三)--InfoFrame
目录 Auxiliary Video information (AVI) InfoFrame AVI InfoFrame包结构 Header Body 举个例子 附录 Audio InfoFrame Audio InfoFrame包结构 Header Body Vendor Specific InfoFrame Vendor Specific InfoFrame包结构 Header Body AVI/AUDIO/VSI Infoframe都…...

【RocketMQ】源码详解:Broker端消息储存流程、消息格式
消息存储流程 入口: org.apache.rocketmq.remoting.netty.NettyRemotingAbstract#processRequestCommand org.apache.rocketmq.broker.processor.SendMessageProcessor#asyncProcessRequest 消息到达broker后会经过netty的解码、消息处理器等,最后根据…...
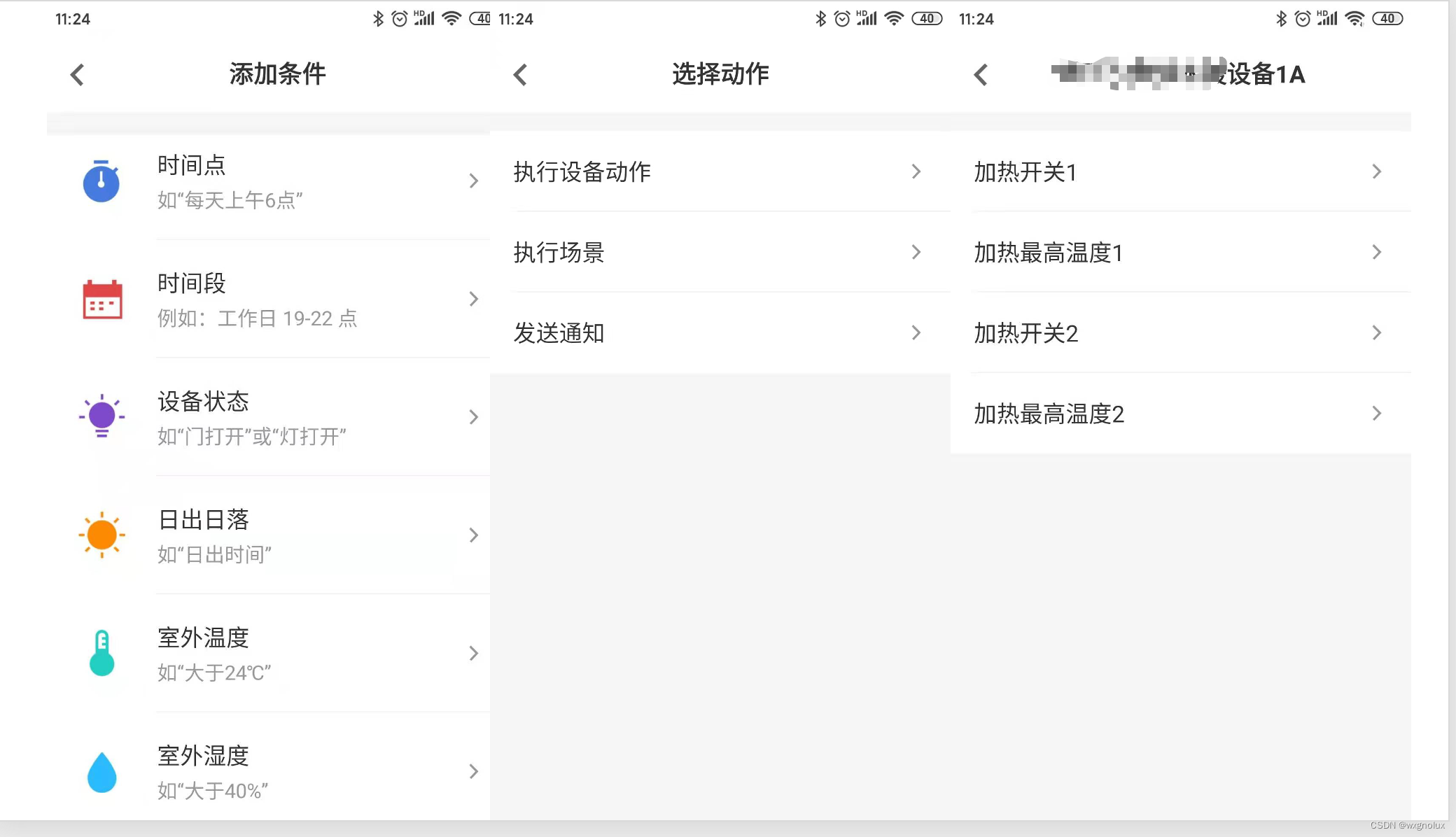
IoT项目系统架构案例2
项目背景 1.这个项目是对之前的案例的升级改造参考:IoT项目系统架构案例_iot案例_wxgnolux的博客-CSDN博客2.基于方案1的项目实施过程中碰到的问题,对硬件设备标准化的理念及新的功能需求(如根据天气预报温度调水温,APP界面可操作性优化等)•采用目前IoT主流厂商的架…...

Vue echarts封装
做大屏的时候经常会遇到 echarts 展示,下面展示在 Vue2.7 / Vue3 中对 echarts (^5.4.0) 的简单封装。 文章首发于https://blog.fxss.work/vue/echarts封装.html,样例查看 echarts 封装使用 props 说明 参数说明类型可选值默认…...
反转字符(不走寻常路))
蓝桥杯入门即劝退(二十二)反转字符(不走寻常路)
欢迎关注点赞评论,共同学习,共同进步! ------持续更新蓝桥杯入门系列算法实例-------- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章…...
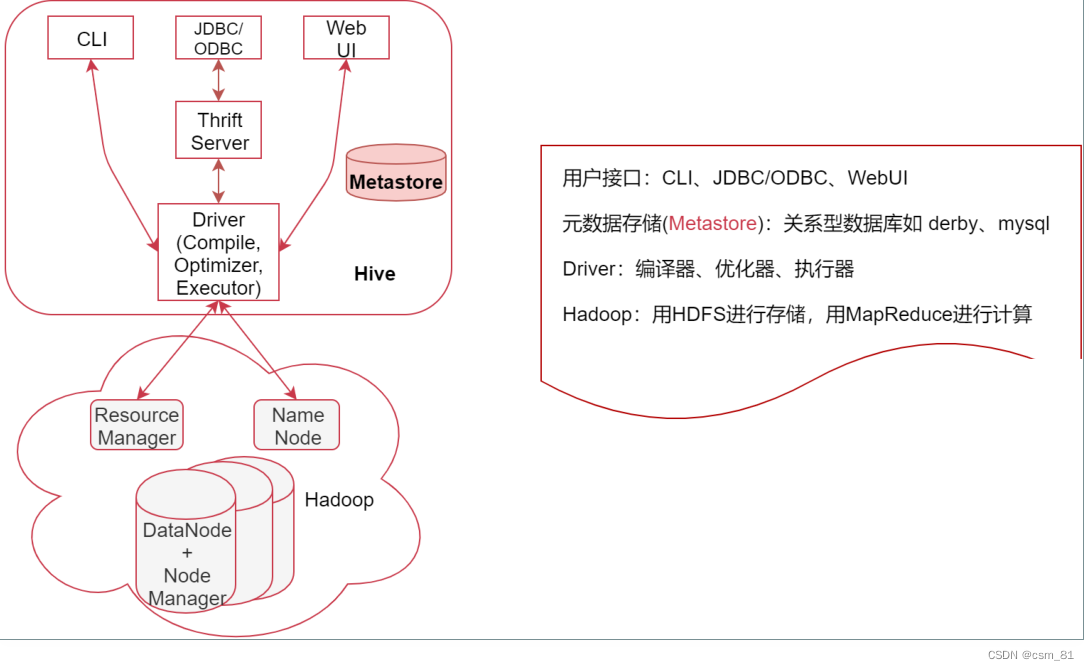
数据仓库Hive
HIve介绍 Hive是建立在Hadoop上的数据仓库基础构架。它提供了一系列的工具,可以用来进行数据提取转化加载,可以简称为ETL。 Hive 定义了简单的类SQL查询语言,称为HQL,它允许熟悉SQL的用户直接查询Hadoop中的数据…...
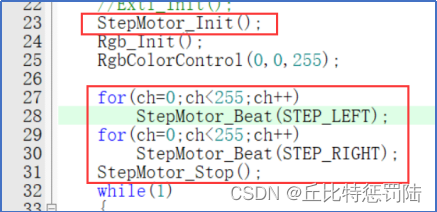
嵌入式 STM32 步进电机驱动,干货满满,建议收藏
目录 步进电机 1、步进电机驱动原理 2、步进电机驱动 3、步进电机应用 1、第一步:初始化IO口 2、设置行进方式 四、源码 步进电机 步进电机被广泛应用于ATM机、喷绘机、刻字机、写真机、喷涂设备、医疗仪器及设备、计算机外设及海量存储设备、精密仪器、工业…...

详讲函数.2.
目录 5. 函数的嵌套调用和链式访问 5.1 嵌套调用 5.2 链式访问 小结: 6. 函数的声明和定义 6.1 函数的声明: 6.2 函数的定义: 5. 函数的嵌套调用和链式访问 函数和函数之间可以根据实际的需求进行组合的,也就是互相调用的…...
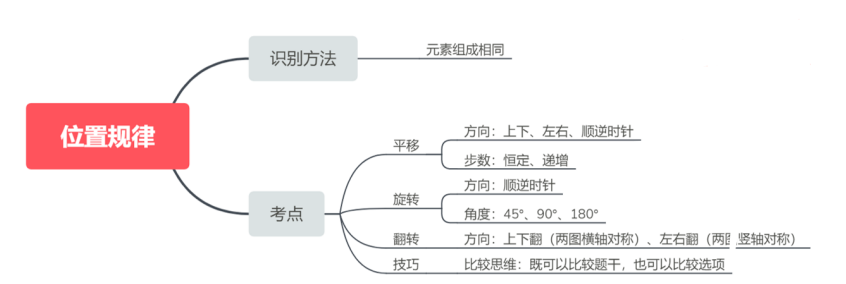
行测-判断推理-图形推理-位置规律-旋转、翻转
短指针每次逆时针旋转60(排除法选C走人)长指针每次顺时针旋转120选C左上菱形每次顺时针旋转90(排除C D)右上每次旋转180(选B走人)左下每次保持不变右下每次逆时针旋转90选B左上和右上为左右翻转,…...

linux shell 入门学习笔记15 shell 条件测试
概念 shell的条件测试目的是得出真和假。 shell 提供的条件测试语法 test 命令 [] 中括号命令 语法*: test条件测试 test命令用来评估一个表达式,他的结果是真,还是假,如果条件为真,那么命令执行状态结果就为0&…...
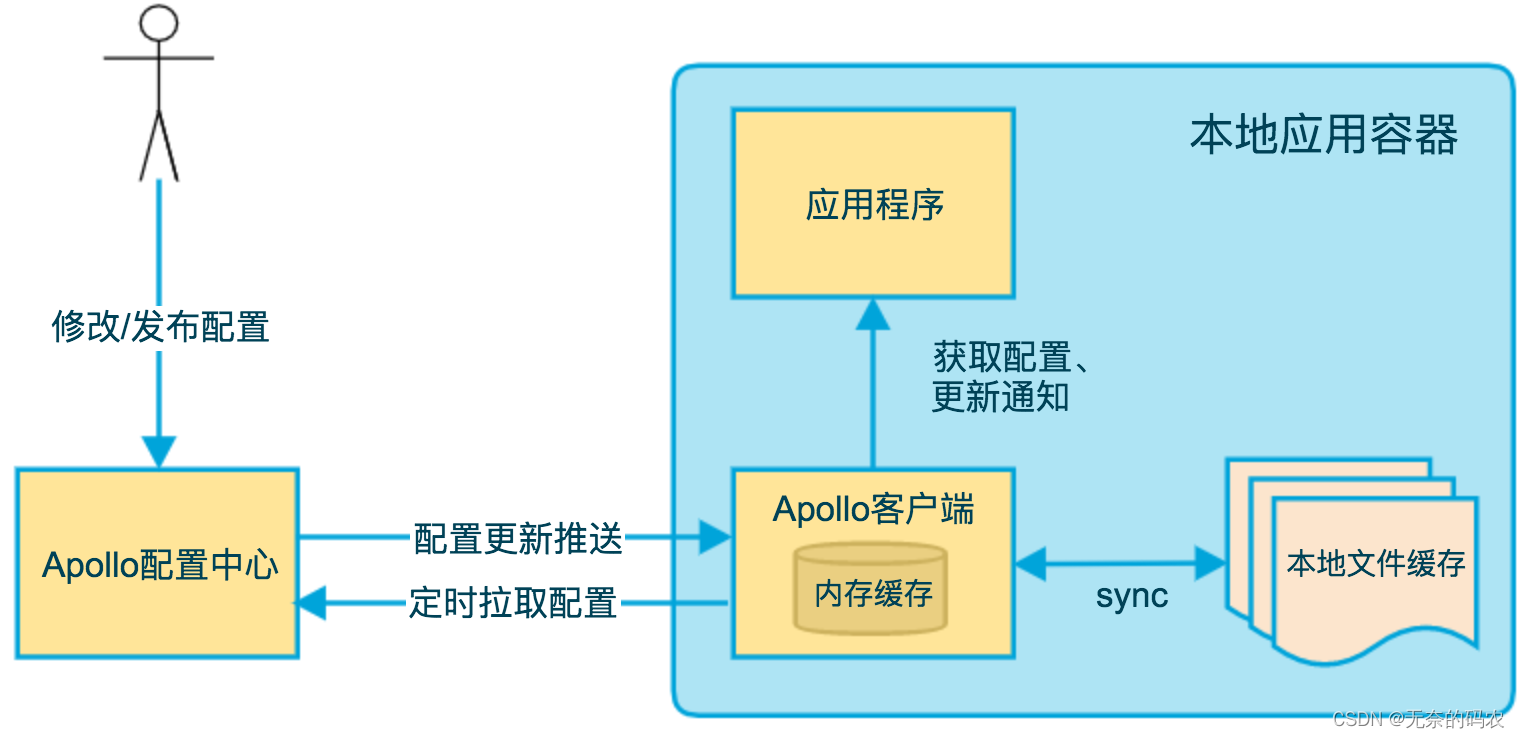
Apollo(阿波罗)分布式配置安装详解
Apollo(阿波罗) Apollo(阿波罗)是携程框架部门研发的分布式配置中心,能够集中化管理应用不同环境、不同集群的配置,配置修改后能够实时推送到应用端,并且具备规范的权限、流程治理等特性&#…...
Vue3之组件
何为组件 组件化的概念已经提出了很多年了,但是何为组件呢?组件有啥优势?本文将会做出解答,首先我们需要弄清楚何为组件。在VUE的官网中的解释是: 组件允许我们将 UI 划分为独立的、可重用的部分,并且可以对…...
【网络】套接字 -- UDP
🥁作者: 华丞臧. 📕专栏:【网络】 各位读者老爷如果觉得博主写的不错,请诸位多多支持(点赞收藏关注)。如果有错误的地方,欢迎在评论区指出。 推荐一款刷题网站 👉 LeetCode刷题网站 文章…...
Lambda原理及应用
Lambda原理及应用 Lambda介绍 Lambda 是 JDK8 以后版本推出的一个新特性,也是一个重要的版本更新,利用 Lambda 可以简化内部类,可以更方便的进行集合的运算,让你的代码看起来更加简洁,也能提升代码的运行效率。 Lambda语法 非…...

运动耳机推荐、最值得入手的运动耳机清单共享
现在市面上各式各样的运动蓝牙耳机着实让人挑花了眼,怎样才能从纷繁复杂的市场中挑选出专业性、安全性、舒适性等各个方面都做地可圈可点的运动蓝牙耳机可真不是一件易事啊,甚至连不少老朋友都会踩坑,为了能让大家挑到真正的运动蓝牙耳机,为此…...
c盘爆满--如何清理电脑C盘
问题 c盘饱满很多天了,今天终于忍无可忍,开始展开对c盘的处理 c盘的基本处理有两步, 第一步,电脑系统清理 1,c盘右键属性,有个磁盘清理,好像是系统更新的一些缓存资源,可以直接清理 当然这只…...

Nginx配置web服务器及部署反向代理
Nginx配置web服务器及部署反向代理配置web服务器location语法部署反向代理代理转发配置web服务器 项目部署到linux上的静态文件代理给Nginx处理。当访问服务器IP时,可以自动返回静态文件主页。 主配置文件中server块对应的次配置include /etc/nginx/conf.d/*.conf…...

mvvm和mvc
mvvm是model-view-viewmodel的缩写,前端开发的架构模式 m: model:模型,指的是数据和交互业务逻辑 v: view:视图,用户看到的ui界面 vm: viewmodel:视图模型࿰…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
