C++---线性dp---传纸条(每日一道算法2023.2.26)
注意事项:
本题dp思路与 “线性dp–方格取数” 一致,下方思路仅证明为什么使用方格取数的思路是正确的。
题目:
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 m
行 n 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 (1,1),小轩坐在矩阵的右下角,坐标 (m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0表示),可以用一个 0∼100的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有 2个用空格隔开的整数 m和 n,表示学生矩阵有 m行n列。
接下来的 m行是一个 m×n的矩阵,矩阵中第 i行 j列的整数表示坐在第 i行 j列的学生的好心程度,每行的 n个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1≤n,m≤50
输入:
3 3
0 3 9
2 8 5
5 7 0
输出:
34
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;const int N = 55;
int w[N][N], f[N+N][N][N]; //注意k要开两倍,因为是i+j的总和
int n, m;int main()
{cin >> n >> m;n = max(n, m); //这里n使用较大的做为边界即可,因为多算几个0不影响结果for (int i = 1; i<=n; i++)for (int j = 1; j<=m; j++) cin >> w[i][j];//线性dpfor (int k = 2; k<=n+m; k++) {for (int i1 = 1; i1<=n; i1++) {for (int i2 = 1; i2<=n; i2++) {// k = i1+j1 = i2+j2, 切记是相等关系int j1 = k-i1, j2 = k-i2;if (j1>=1 && j2>=1 && j1<=n && j2<=n) { //判断j1和j2的合法性//如果是重叠点就只加一次,例如(1,2)(1,2), 如果是非重叠点就将两个点都加上,例如(1, 2)(2, 1)int t = w[i1][j1];if (i1 != i2) t += w[i2][j2];//引用节省代码量,分四种情况讨论上两个点如何进行移动int &x = f[k][i1][i2];x = max(x, f[k-1][i1-1][i2-1]); //down,downx = max(x, f[k-1][i1-1][i2]); //down,rightx = max(x, f[k-1][i1][i2-1]); //right,downx = max(x, f[k-1][i1][i2]); //right, rightx += t;}}}}cout << f[n+m][n][n];return 0;
}
思路:
这里直接贴vlehr大佬的画图解释(原链接):
已经讲的非常清晰了,自认讲不明白,就借用下大佬的吧哎嘿~
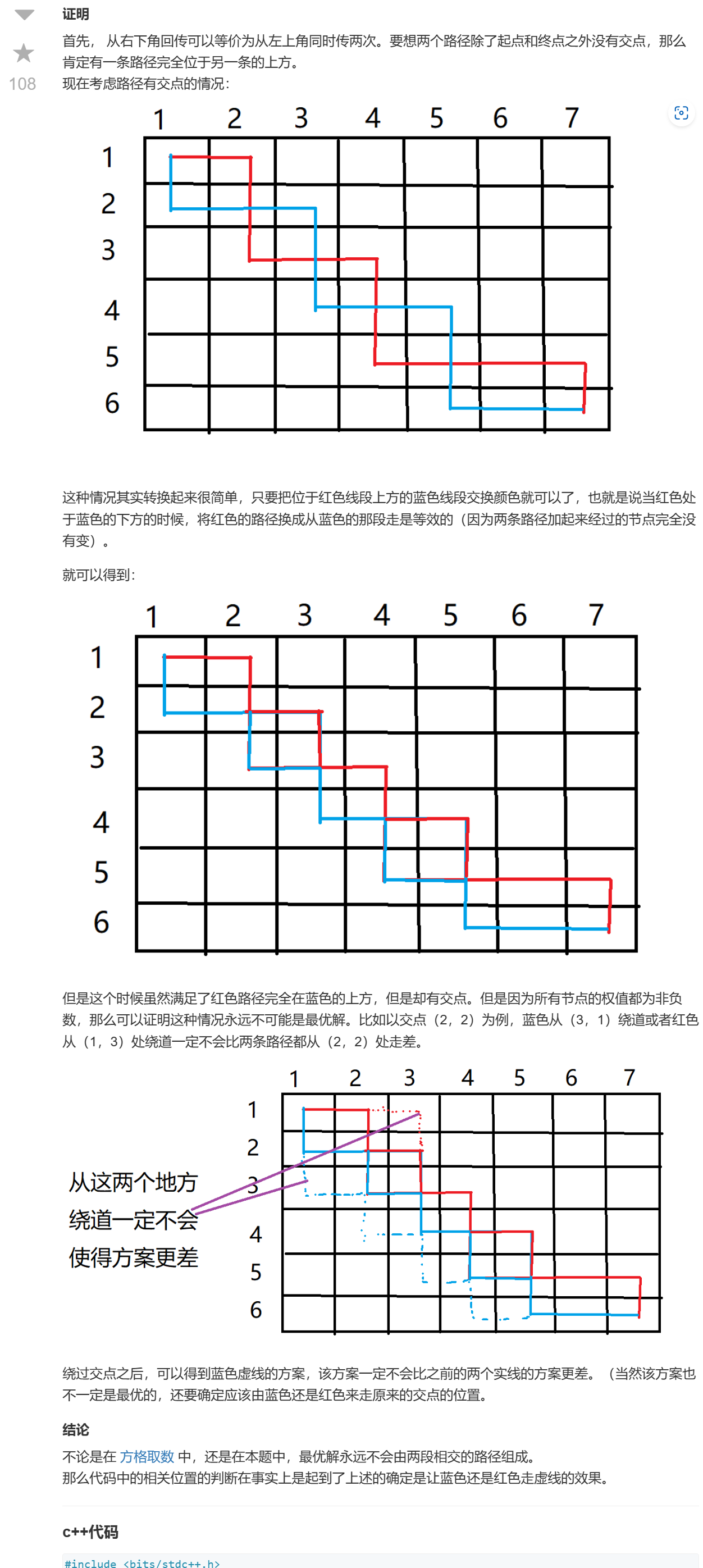
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流
添加链接描述
相关文章:

C++---线性dp---传纸条(每日一道算法2023.2.26)
注意事项: 本题dp思路与 “线性dp–方格取数” 一致,下方思路仅证明为什么使用方格取数的思路是正确的。 题目: 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。 一次素质拓展活动中,班上同学安排坐成…...

浅谈 C/C++ 的输入输出
更好的阅读体验\huge{\color{red}{更好的阅读体验}}更好的阅读体验 文章目录0. 叠甲,过1. 谈谈输入输出缓冲区1.1 基本概念输入输出流标准输入输出流文件输入输出流1.2 输入输出缓冲区什么是输入输出缓冲区?为什么要设置输入输出缓冲区?C/C 的…...
【计算机三级网络技术】 第二篇 中小型系统总体规划与设计
文章目录一、基于网络的信息系统基本结构二、划分网络系统组建工程阶段三、网络需求调研与系统设计原则四、网络用户调查与网络工程需求分析1.网络用户调查2.网络节点的地理位置分布3.应用概要分析4.网络需求详细分析五、网络总体设计基本方法1.网络工程建设总体目标与设计原则…...
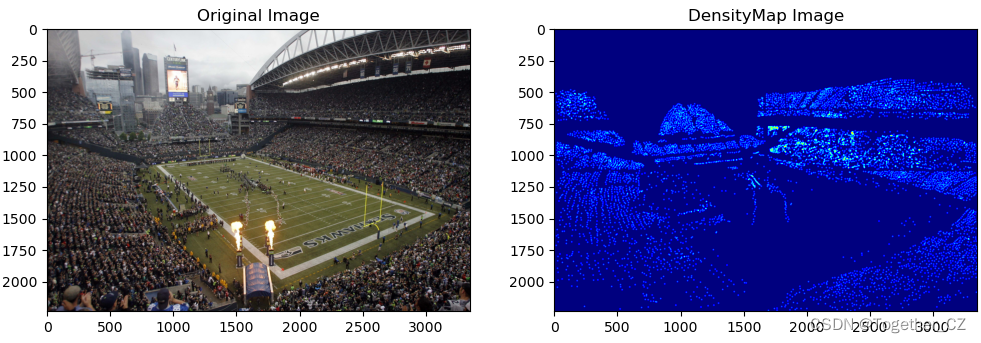
Boosting Crowd Counting via Multifaceted Attention之人群密度估计实践
这周闲来无事,看到一篇前不久刚发表的文章,是做密集人群密度估计的,这块我之前虽然也做过,但是主要是基于检测的方式实现的,这里提出来的方法还是比较有意思的,就拿来实践一下。论文在这里,感兴…...
python之面向对象编程
1、面向对象介绍: 世界万物,皆可分类 世界万物,皆为对象 只要是对象,就肯定属于某种类 只要是对象,就肯定有属性 2、 面向对象的几个特性: class类: 一个类即对一类拥有相同属性的对象的…...
(七))
常见前端基础面试题(HTML,CSS,JS)(七)
同源策略 浏览器有一个重要的安全策略,称之为同源策略 其中,协议、端口号、域名必须一致,,称之为同源,两个源不同,称之为跨源或跨域 同源策略是指,若页面的源和页面运行过程中加载的源不一致…...

产业链金风控基本逻辑
产业链金风控基本逻辑 产业链金融平台作为一个助贷平台,很大程度上是为银行等金融机构进 行引流,贷款的审批本质上还是依赖金融机构的风控。那么,产业链金融 平台是否还有必要建设自己的风控模型呢?笔者给出的答案是肯定的。 一方面&#x…...
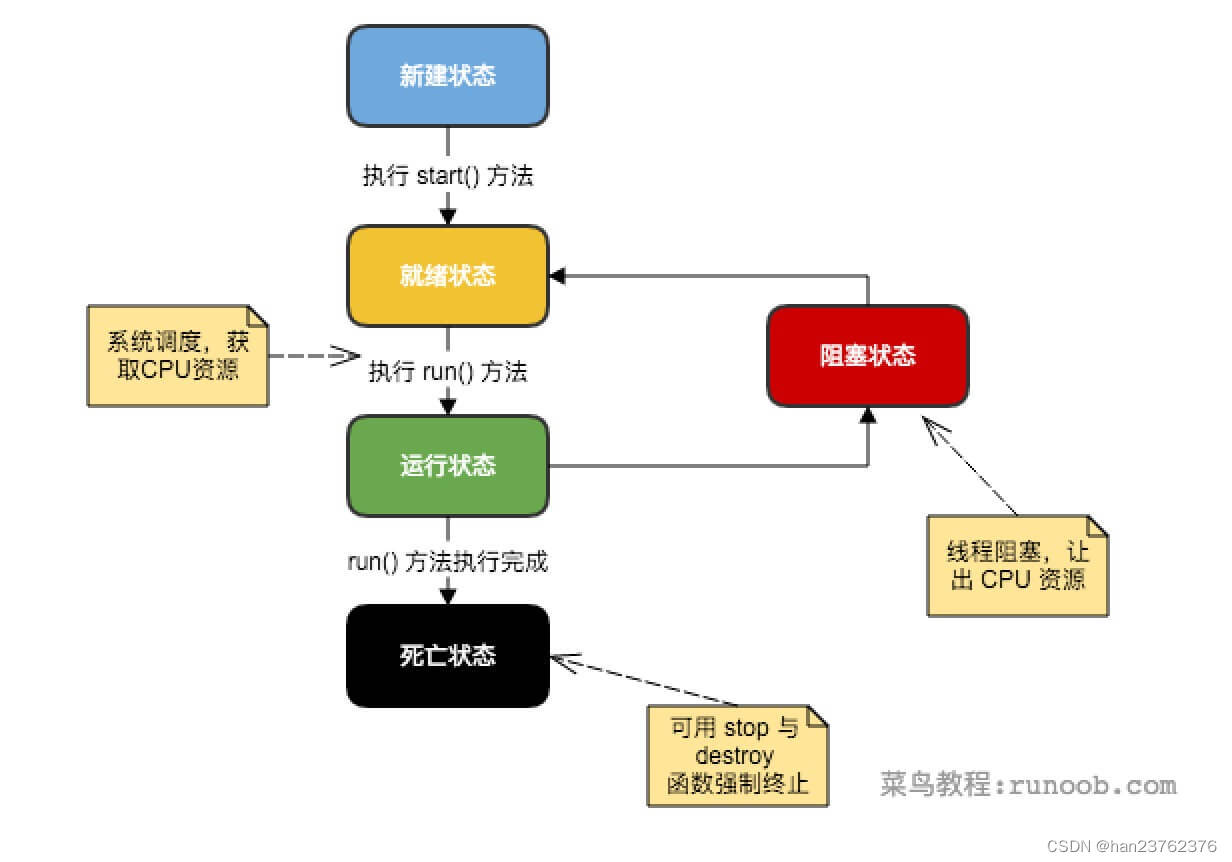
Java高级点的知识
Java 集合框架 该框架必须是高性能的。基本集合(动态数组,链表,树,哈希表)的实现也必须是高效的。 该框架允许不同类型的集合,以类似的方式工作,具有高度的互操作性。 对一个集合的扩展和适应…...
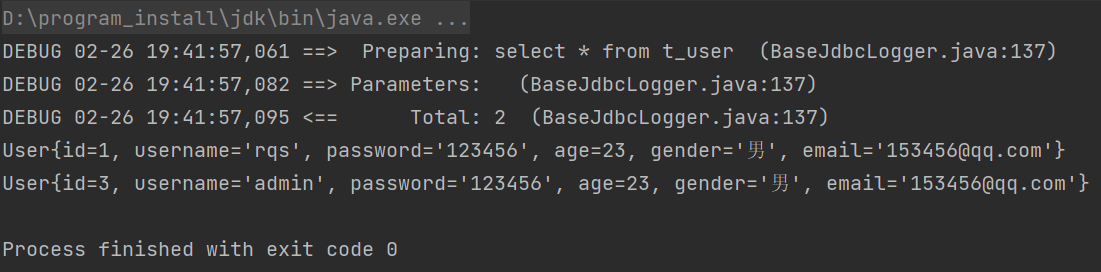
MyBatis - 05 - 封装SqlSessionUtil工具类(用于获取SqlSession对象)并测试功能
文章目录1.新建SqlSessionUtils工具类2.编写静态方法3.项目结构及代码项目结构数据库和表pom.xmlParameterMapper接口:User类:ParameterMapper.xmljdbc.propertieslog4j.xml:mybatis-config.xml:ParameterMapperTest测试类:测试结果1.新建Sql…...
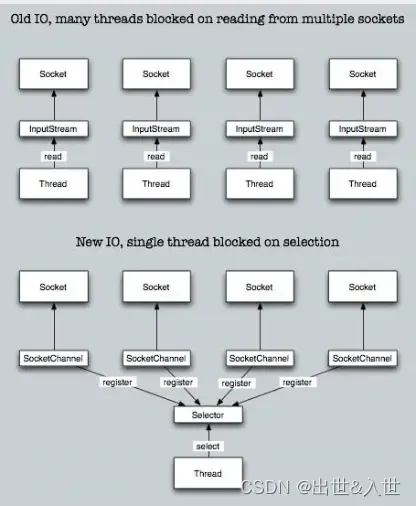
Java中BIO、NIO和AIO的区别和应用场景
IO的方式通常分为几种,同步阻塞的BIO、同步非阻塞的NIO、异步非阻塞的AIO。 一、BIO 在JDK1.4出来之前,我们建立网络连接的时候采用BIO模式,需要先在服务端启动一个ServerSocket,然后在客户端启动Socket来对服务端进行通信&#…...

Python安装教程(附带安装包)
首先,打开python安装包的下载地址,https://www.python.org/downloads/,会有些慢 点击downloads中的windows 左侧是稳定的版本,我这边下的是3.8的,不想去官网下载的可以直接用我下载的这个3.8版本,https://…...

华为OD机试用Python实现 -【信号发射和接收】(2023-Q1 新题)
华为OD机试题 华为OD机试300题大纲信号发射和接收题目描述输入描述输出描述说明示例一输入输出说明示例二输入输出说明Python 代码实现代码运行结果代码编写思路华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为…...

Springboot整合 Thymeleaf增删改查一篇就够了
很早之前写过Thymeleaf的文章,所以重新温习一下,非前后端分离,仅仅只是学习 官网: https://www.thymeleaf.org/ SpringBoot可以快速生成Spring应用,简化配置,自动装配,开箱即用。 JavaConfigur…...

BigScience bloom模型
简介项目叫 BigScience,模型叫 BLOOM,BLOOM 的英文全名代表着大科学、大型、开放科学、开源的多语言语言模型。拥有 1760 亿个参数的模型.BLOOM 是去年由 1000 多名志愿研究人员,学者 在一个名为“大科学 BigScience”的项目中创建的.BLOOM 和今天其他可用大型语言模型存在的一…...

Squid服务的缓存概念
Squid缓存概念 squid是一个缓存服务器的守护进程 之前涉及的缓存服务:redis 2-8原则:80%的访问就是从20%的数据提供的;因此把20%的数据给到缓存–>完美解决等待时间; nginx是没有缓存的服务的;那么专业的事情就…...
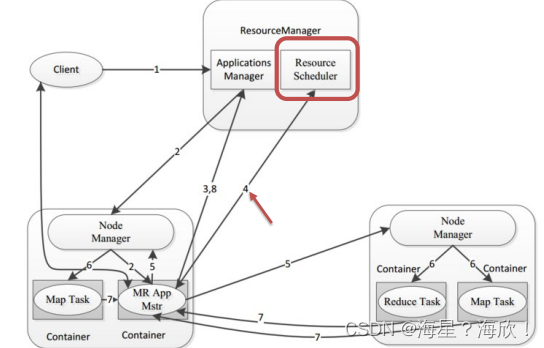
Hadoop YARN
目录Hadoop YARN介绍Hadoop YARN架构、组件程序提交YARN交互流程YARN资源调度器Scheduler调度器策略FIFO SchedulerCapacity SchedulerFair SchedulerHadoop YARN介绍 YARN是一个通用资源管理系统和调度平台,可为上层应用提供统一的资源管理和调度 上图࿱…...

使用 Macrobenchmark 测试 Android 应用性能
etpack Compose 是推荐用于构建原生 Android 界面的新工具包。后续简称Jetpack Compose为Compose。在了解State之前需要先对Compose及申明性编程式有个大概的了解。State初体验好了,在你有一定了解的基础上,我们先来运行几个Demo,初步了解为何…...
【django】django-simpleui配置后,后台显示空白页解决方法
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 django后台显示空白页解决方法 1. 正文 添加完simpleui以后,后台显示一片空白,一脸问号??? …...
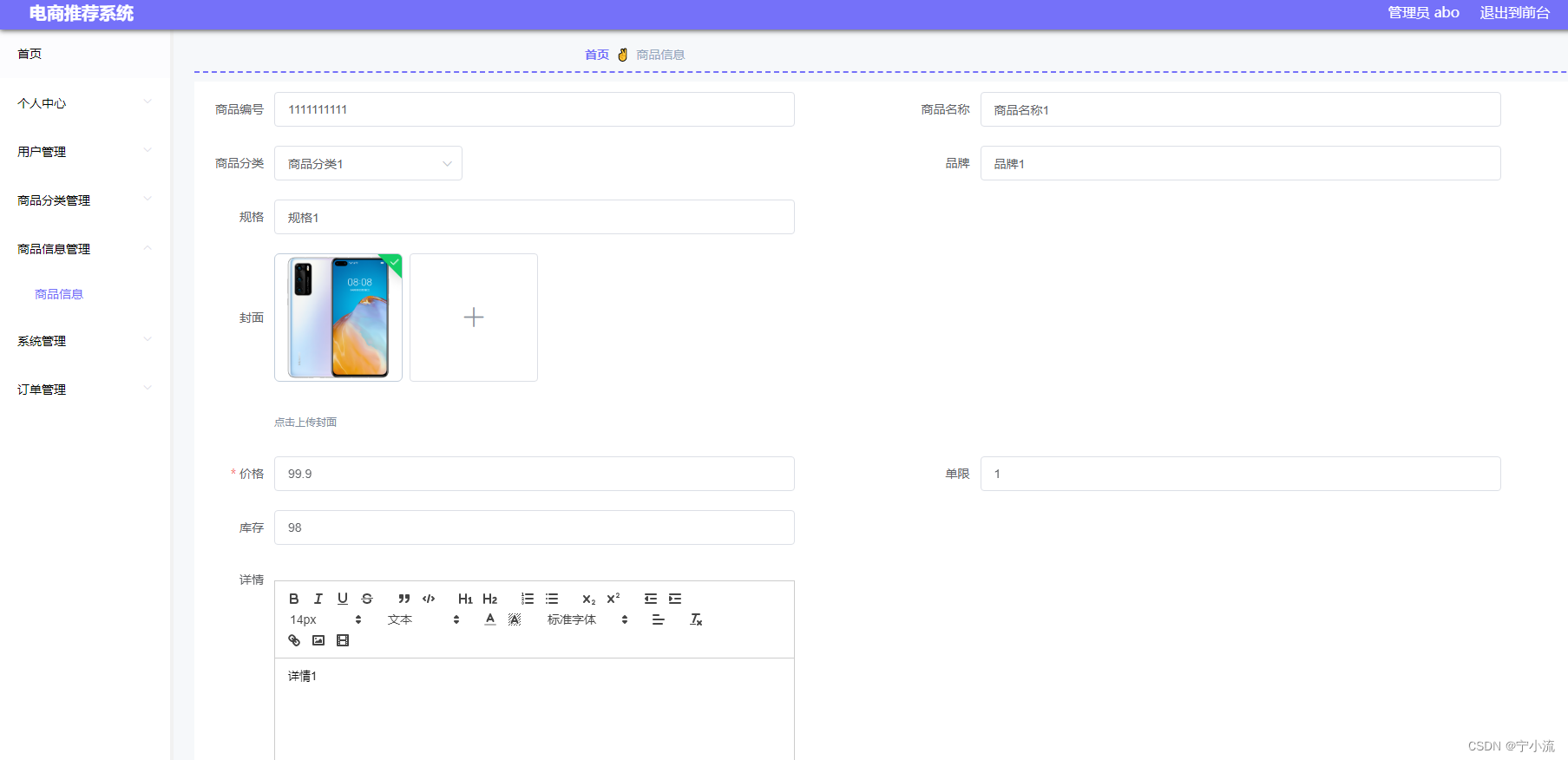
【035】基于Vue的电商推荐管理系统(含源码数据库、超详细论文)
摘 要:基于Vue+Nodejs+mysql的电商推荐管理系统,这个项目论文超详细,er图、接口文档、功能展示、技术栈等说明特别全!!! (文末附源码数据库、课设论文获取方式࿰…...

【c++】模板1—函数模板
文章目录函数模板语法函数模板注意事项案例—数组选择排序普通函数和函数模板的区别普通函数和函数模板调用规则模板的局限性函数模板语法 函数模板作用: 建立一个通用函数,其函数返回值类型和形参类型可以不具体制定,用一个虚拟的类型来代表…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

汇编语言学习(三)——DoxBox中debug的使用
目录 一、安装DoxBox,并下载汇编工具(MASM文件) 二、debug是什么 三、debug中的命令 一、安装DoxBox,并下载汇编工具(MASM文件) 链接: https://pan.baidu.com/s/1IbyJj-JIkl_oMOJmkKiaGQ?pw…...
