基础数据结构--线段树(Python版本)
文章目录
- 前言
- 特点
- 操作
- 数据存储
- update
- Lazy下移
- 查询
- 实现
前言
月末了,划个水,赶一下指标(更新一些活跃值,狗头)
本文主要是关于线段树的内容。这个线段树的话,主要是适合求解我们一个数组的一些区间的问题,例如区间之和,区间乘机,区间最大,最小值等(当然求和,求乘机啥的,直接用前缀数组,如果是一些区间的大小的问题的话,当然用这个是比较合适的,当然这依然是空间换取时间的操作。例如一个数组长度为N,那么当我们构建这颗线段树时,我们所需要花费的空间为4N(为了保证不越界).
特点
首先的话,要说的关于线段树的特点其实就几个,第一就是数据存放在叶子节点,非叶子节点表示的是我们想要求取的目标值,例如我们想要求取一个区间和,那么非叶子节点存储的就是这个小区间内的值。
第二个特点就是Lazy懒惰更新,这个有点类似于摊还分析当中提到的第二种方式,每个元素的花费需要考虑到当前的消费和将来的消费,将来的消费,用于将来的花费。这个Lazy其实也有类似的意思,我先标记一下,然后我要用的到的时候,我再进行操作,起到了一个预知未来,延迟操作的意思。同样的,代码实现比较简单,至少比红黑树,斐波那契堆简单。
那么关于这个特点的话,这里先插一个眼,具体的将在下面进行阐述。
本文的话,就从区间求和为案例进行说明,这里面可以覆盖到较多的操作。
操作
数据存储
首先的话,这个数据的存储其实就是下面的样子。
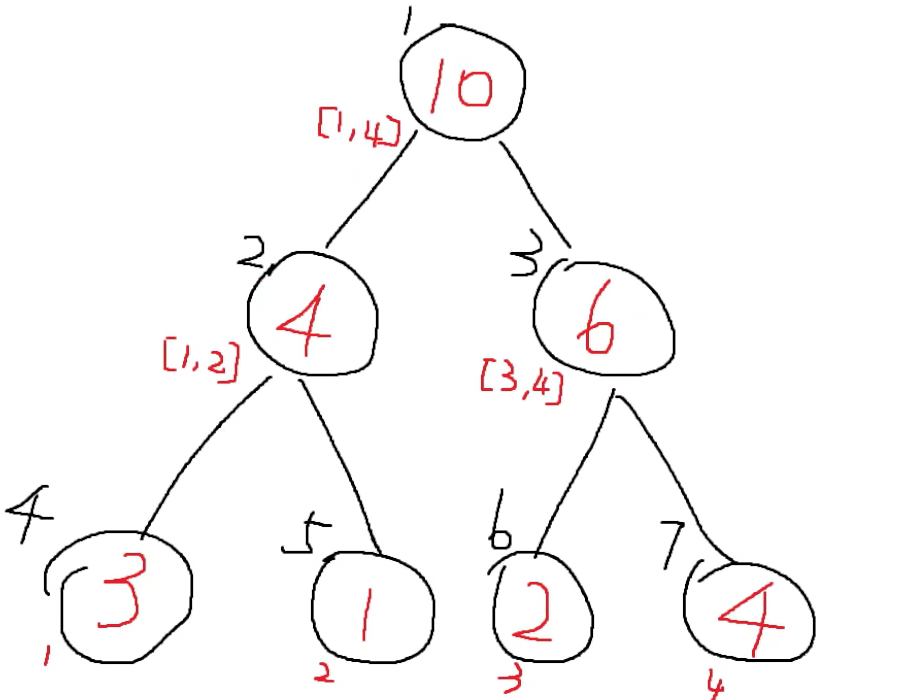
然后这个叶子节点的话就是我们的这个数据,然后的话,这里也是对半砍掉一组数据,然后递归,跟那个归并有点像。
update
然后就是修改,这个的话就开始体现到Lazy的作用了,首先我们知道一个节点,他其实表示了当前这个节点表示的是哪个区间的一个值,用代码表示他的一个数据结构其实就是这样的:
class __Node():l: int = 0r: int = 0v: int = 0lazy: int = 0def __str__(self):return "left:{},right{},value:{},lazy:{}".format(self.l, self.r, self.v, self.lazy)所以这个Update的话,明确一个区间,然后呢,我们找到这个区间,然后秉承着lazy的原则,如果我们发现,如果我们要更新的区间能够覆盖我们当前的这个节点的区间,我们就直接更新好这个节点的值,然后这个Lazy,记录一些我们修改的值是啥。
def update(self, i, l, r, k):if (self.tree[i].l >= l and self.tree[i].r <= r):self.tree[i].v += k * (self.tree[i].r - self.tree[i].l + 1)self.tree[i].lazy = kreturnif (self.tree[i].lazy != 0):self.__putdown(i)if (self.tree[2 * i].r >= l): #和左孩子还有交集self.update(2 * i, l, r, k)if (self.tree[2 * i + 1].l <= r): #和右孩子还有交集self.update(2 * i + 1, l, r, k)self.tree[i].v = self.tree[2*i].v+self.tree[2*i+1].v
之后的话,我们跟新一下,当然这里还需要注意的是,就是如果没有完全覆盖的话,我们需要更新一下Lazy,此时给到孩子节点,为什么要更新呢,原因的话就是当前的节点已经不能覆盖了,需要用到孩子节点,但是原来孩子节点没有更新值,现在要用了,就得把孩子赶紧更新一下,然后重新更新当前作为父节点的i。
Lazy下移
这个下移的话就是刚刚提到的,因为这个Lazy就相当于一个标记。他是这样的。
def __putdown(self, i):self.tree[2 * i].lazy += self.tree[i].lazyself.tree[2 * i + 1].lazy += self.tree[i].lazymid = (self.tree[i].l + self.tree[i].r) // 2self.tree[2 * i].v += self.tree[i].lazy * (mid - self.tree[i].l + 1)self.tree[2 * i + 1].v += self.tree[i].lazy * (self.tree[i].r - mid)self.tree[i].lazy = 0更新孩子的Lazy,然后去掉父节点的Lazy,然后更新值。
查询
查询也是一致的,和更新一样,只是少了元素的更新,这里依然需要这个Lazy的下移,而且其实这个Lazy的下移其实就是在重新计算我们的修改,假设一直都没有用到,就一直不会更新,这样就节省了运算。就比如,你买了一张4080ti,但是你一直没有时间happy,那么在你没有happy时间的情况下就提前买了显卡,那么就浪费了这个money,因为早买没有享受到,但是当你有happy time的时候,你再去买,那么就是及时享乐了,没有造成资源的空闲浪费,搞不好还降价了,嘿嘿~
def search(self, i, l, r):if (self.tree[i].l >= l and self.tree[i].r <= r):return self.tree[i].vif (self.tree[i].lazy != 0):self.__putdown(i)t = 0if (self.tree[2 * i].r >= l):t += self.search(2 * i, l, r)if (self.tree[2 * i + 1].l <= r):t += self.search(2 * i + 1, l, r)return t
实现
"""
为了方便建树,这里的话我们将从1开始作为我们的下标
"""
class SegmentTree(object):def __init__(self, date):self.date = [0] + dateself.len_date = len(self.date)self.tree = [self.__Node() for _ in range(4 * self.len_date)]self.__build(1, 1, self.len_date - 1)def __build(self, i, l, r):self.tree[i].l = lself.tree[i].r = rif (l == r):self.tree[i].v = self.date[r]returnmid = (l + r) // 2self.__build(2*i, l, mid)self.__build(2*i+1, mid + 1, r)self.tree[i].v = self.tree[i * 2].v + self.tree[i * 2 + 1].vdef search(self, i, l, r):if (self.tree[i].l >= l and self.tree[i].r <= r):return self.tree[i].vif (self.tree[i].lazy != 0):self.__putdown(i)t = 0if (self.tree[2 * i].r >= l):t += self.search(2 * i, l, r)if (self.tree[2 * i + 1].l <= r):t += self.search(2 * i + 1, l, r)return tdef update(self, i, l, r, k):if (self.tree[i].l >= l and self.tree[i].r <= r):self.tree[i].v += k * (self.tree[i].r - self.tree[i].l + 1)self.tree[i].lazy = kreturnif (self.tree[i].lazy != 0):self.__putdown(i)if (self.tree[2 * i].r >= l):self.update(2 * i, l, r, k)if (self.tree[2 * i + 1].l <= r):self.update(2 * i + 1, l, r, k)self.tree[i].v = self.tree[2*i].v+self.tree[2*i+1].vdef __putdown(self, i):self.tree[2 * i].lazy = self.tree[i].lazyself.tree[2 * i + 1].lazy = self.tree[i].lazymid = (self.tree[i].l + self.tree[i].r) // 2self.tree[2 * i].v += self.tree[i].lazy * (mid - self.tree[i].l + 1)self.tree[2 * i + 1].v += self.tree[i].lazy * (self.tree[i].r - mid)self.tree[i].lazy = 0class __Node():l: int = 0r: int = 0v: int = 0lazy: int = 0def __str__(self):return "left:{},right{},value:{},lazy:{}".format(self.l, self.r, self.v, self.lazy)这里的话,注意,找的时候呢,是从1号节点开始的,1号节点不等于第一个元素!
if __name__ == '__main__':a = [1,2,3,4,5]seg = SegmentTree(a)seg.update(1,5,5,5) #从根节点开始找,更新区间为[5,5]的元素+5,也就是第五个元素+5print(seg.search(1, 4, 5))#从根节点开始找,查找区间为[4,5]的区间和
🆗,over!
相关文章:

基础数据结构--线段树(Python版本)
文章目录前言特点操作数据存储updateLazy下移查询实现前言 月末了,划个水,赶一下指标(更新一些活跃值,狗头) 本文主要是关于线段树的内容。这个线段树的话,主要是适合求解我们一个数组的一些区间的问题&am…...

【micropython】SPI触摸屏开发
背景:最近买了几块ESP32模块,看了下mircopython支持还不错,所以买了个SPI触摸屏试试水,记录一下使用过程。硬件相关:SPI触摸屏使用2.4寸屏幕,常见淘宝均可买到,驱动为ILI9341,具体参…...
【云原生】k8s中Pod进阶资源限制与探针
一、Pod 进阶 1、资源限制 当定义 Pod 时可以选择性地为每个容器设定所需要的资源数量。 最常见的可设定资源是 CPU 和内存大小,以及其他类型的资源。 当为 Pod 中的容器指定了 request 资源时,调度器就使用该信息来决定将 Pod 调度到哪个节点上。当还…...
AI - stable-diffusion(AI绘画)的搭建与使用
最近 AI 火的一塌糊涂,除了 ChatGPT 以外,AI 绘画领域也有很大的进步,以下几张图片都是 AI 绘制的,你能看出来么? 一、环境搭建 上面的效果图其实是使用了开源的 AI 绘画项目 stable-diffusion 绘制的,这是…...
应用场景五: 西门子PLC通过Modbus协议连接DCS系统
应用描述: 西门子PLC(S7200/300/400/200SMART)通过桥接器可以支持ModbusRTU串口和ModbusTCP以太网(有线和无线WIFI同时支持)两种通讯方式连接DCS系统,不需要编程PLC通讯程序,直接在模块中进行地…...

我继续问了ChatGPT关于SAP顾问职业发展前景的问题,大家感受一下
目录 SAP 顾问 跟其他IT工作收入情况相比是怎么样的? 如何成为SAP FICO 优秀的顾问 要想成为SAP FICO 优秀的顾问 ,需要ABA开发技能吗 SAP 顾问中哪个类型收入最多? 中国的ERP软件能够取代SAP吗? 今天我继续撩 ChatGPT。随便问…...
)
Python小白入门---00开篇介绍(简单了解一下)
Python 小白入门 系列教程 第一部分:Python 基础 介绍 Python 编程语言安装 Python 环境变量和数据类型运算符和表达式控制流程语句函数和模块异常处理 第二部分:Python 标准库和常用模块 Python 标准库简介文本处理和正则表达式文件操作和目录操作时…...

【算法基础】C++STL容器
一、Vector 1. 初始化(定义) (1)vector最基本的初始化: vector <int> a;(2)定义长度为10的vector: vector <int> a(10);(3)定义长度为10的vector,并且把所有元素都初始化为-3: vector <int...

【经典蓝牙】蓝牙 A2DP协议分析
A2DP 介绍 A2DP(Advanced Audio Distribution Profile)是蓝牙高音质音频传输协议, 用于传输单声道, 双声道音乐(一般在 A2DP 中用于 stereo 双声道) , 典型应用为蓝牙耳机。 A2DP旨在通过蓝牙连接传输高质量的立体声音…...
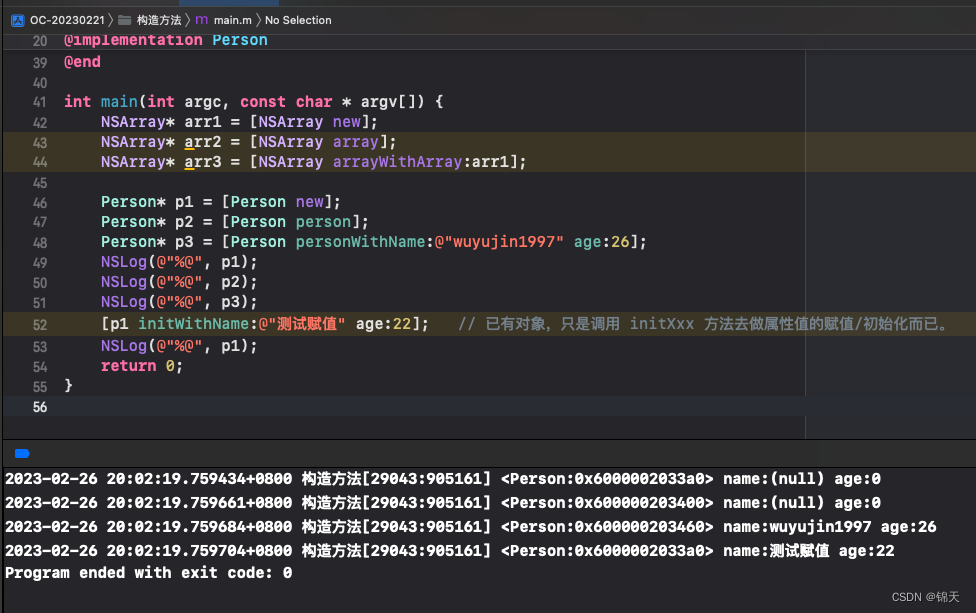
Objective-C 构造方法的定义和声明规范
总目录 iOS开发笔记目录 从一无所知到入门 文章目录源码中 NSArray 的构造方法与命名规律自定义类的构造方法命名截图代码输出源码中 NSArray 的构造方法与命名规律 interface NSArray<ObjectType> (NSArrayCreation) (instancetype)array;(instancetype)arrayWithObject…...

Matlab图像处理学习笔记
Matlab图像处理 Matlab基础 数组 1、向量 生成方式1: x = [值] x = [1 2 3] % 行向量 y = [4; 5; 6] % 列向量 z = x % 行向量转列向量...
——迭代器的基础理论知识)
笔记(三)——迭代器的基础理论知识
迭代器是一种检查容器内元素并且遍历容器内元素的数据类型。它提供对一个容器中的对象的访问方法,并且定义了容器中对象的范围。一、vector容器的iterator类型vector容器的迭代器属于随机访问迭代器,一次可以移动多个位置。vector<int>::iterator …...
没有公网ip怎么外网访问nas?快解析内网端口映射到公网
对于NAS用户而言,外网访问是永远绕不开的话题。拥有NAS后的第一个问题,就是搞定NAS的外网访问。不过众所周知,并不是所有的小伙伴都能得到公网IP,由于IPV4资源的枯竭,一般不会被分配到公网IP。公网IP在很大程度上除了让…...
spring integration使用:消息转换器
系列文章目录 …TODO spring integration开篇:说明 …TODO spring integration使用:消息路由 spring integration使用:消息转换器 spring integration使用:消息转换器系列文章目录前言消息转换器(或者叫翻译器&#x…...
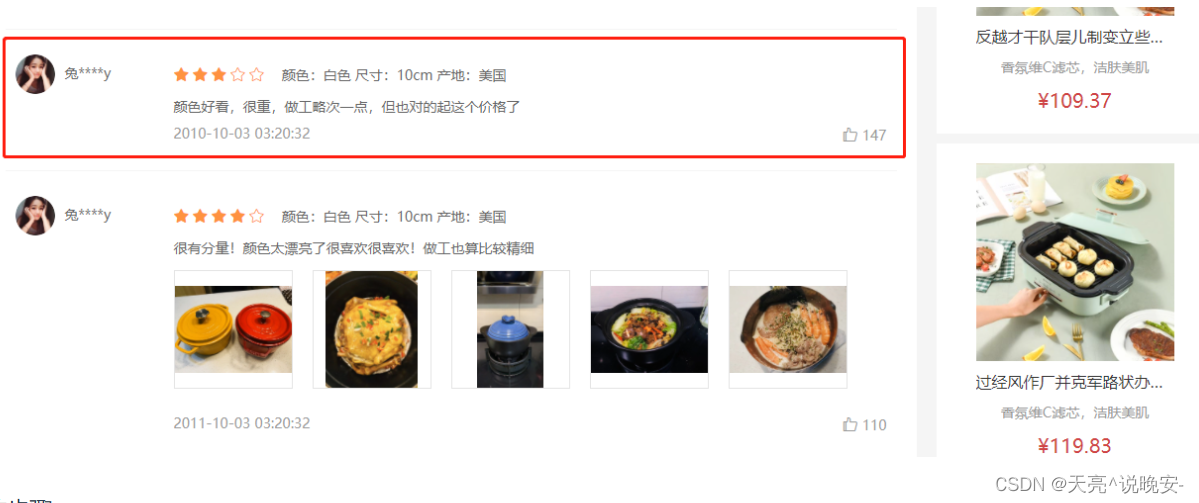
Vue3电商项目实战-商品详情模块7【21-商品详情-评价组件-头部渲染、22-商品详情-评价组件-实现列表】
文章目录21-商品详情-评价组件-头部渲染22-商品详情-评价组件-实现列表21-商品详情-评价组件-头部渲染 目的:根据后台返回的评价信息渲染评价头部内容。 yapi 平台可提供模拟接口,当后台接口未开发完毕或者没有数据的情况下,可以支持前端的开…...

地址,指针,指针变量是什么?他们的区别?符号(*)在不同位置的解释?
指针是C语言中的一个重要概念,也是C语言的一个重要特色;使用指针,可以使程序简洁、紧凑、高效。不掌握指针,就没有掌握C语言的精华。 目录 一、定义 1.1地址 1.2指针 1.3指针变量 1.4指针和指针变量的区别 二、使用指针变量…...
【MongoDB】一、MongoDB的安装与部署
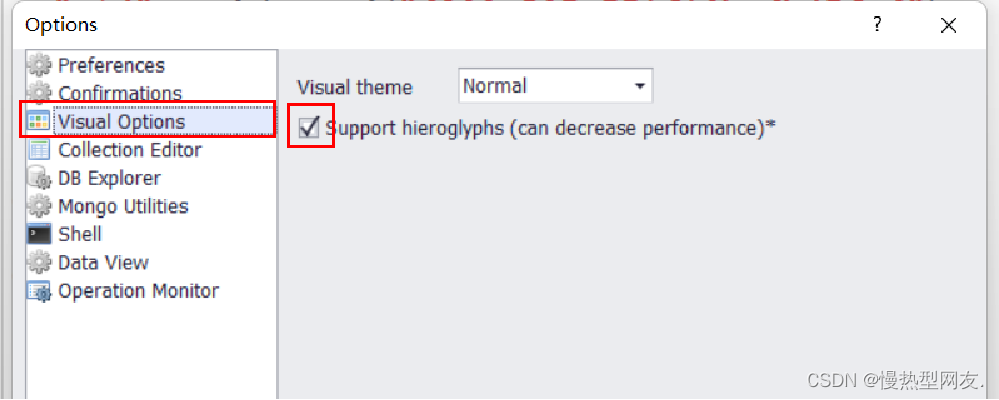
【MongoDB】一、MongoDB的安装与部署实验目的实验内容实验步骤一、下载MongoDB安装包二、创建文件夹data及子文件夹db和log三、启动MongDB服务1. 在命令行窗口执行启动MongoDB服务命令2. 打开mongodb.log3. 打开浏览器进行启动验证四、登录MongoDB五、配置环境变量六、将MongDB…...

《爆肝整理》保姆级系列教程python接口自动化(二十三)--unittest断言——上(详解)
简介 在测试用例中,执行完测试用例后,最后一步是判断测试结果是 pass 还是 fail,自动化测试脚本里面一般把这种生成测试结果的方法称为断言(assert)。用 unittest 组件测试用例的时候,断言的方法还是很多的…...

MySQL的mvcc
mvcc(多版本并发控制) MVCC 是通过数据行的多个版本管理来实现数据库的并发控制 。使得在InnoDB的事务隔离级别下执行 一致性读操作有了保证。可以认为是行级锁的变种,在很多情况下可以避免加锁,开销更低 mvcc没有正式的标准&…...
vite:常见的配置
最近在捣鼓一下vite,因为自己一直在使用react,就选择vite、react来体验一下vite。 使用最简单的方法创建一个应用:yarn create vite,然后选择react框架。 vite默认配置是使用了defineConfig工具函数: import { defi…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
