西瓜书读书笔记整理(七)—— 第七章 贝叶斯分类器
第七章 贝叶斯分类器
- 7.1 贝叶斯决策论(Bayesian Decision Theory)
- 7.1.1 先验概率(Prior Probability)
- 7.1.2 后验概率(Posterior Probability)
- 7.1.3 似然度(Likelihood)
- 7.1.4 决策规则(Decision Rule)
- 7.1.5 期望损失(Expected Loss)
- 7.1.6 条件风险(Conditional Risk)
- 7.1.7 总体风险(Aggregate Risk)
- 7.1.8 贝叶斯理论
- 7.1.8 贝叶斯决策论(Bayesian Decision Theory)
- 7.1.9 贝叶斯决策步骤
- 7.2 极大似然估计(Maximum Likelihood Estimation)
- 7.2.1 频率主义(Frequentist)与概率主义(Bayesian)
- 7.2.2 极大似然估计(Maximum Likelihood Estimation)
- 7.2.3 极大似然估计是一种基于频率主义思想的统计方法
- 7.2.4 贝叶斯网络与极大似然估计方法之间的关系
- 7.3 朴素贝叶斯分类器(Naive Bayes Classifier)与半朴素贝叶斯分类器(Semi-Naive Bayes Classifier)
- 7.5 贝叶斯网(Bayesian Network)
- 7.5.1 结构
- 7.5.2 学习
- 7.5.3 推断
- 7.5.4 吉布斯采样算法(ibbs sampling)
- 7.6 EM (Expectation-Maximization)算法
- 7.6.1 EM 算法概述
- 7.6.2 EM 算法与贝叶斯网络
- 7.7 总结
7.1 贝叶斯决策论(Bayesian Decision Theory)
为了解释清楚什么是贝叶斯决策论,需先约定好以下几个概念。
7.1.1 先验概率(Prior Probability)
先验概率 是指这是在进行决策之前已知的概率分布,反映了不确定性的先验知识。先验概率通常是基于以往经验或领域知识估计的。
7.1.2 后验概率(Posterior Probability)
后验概率 是在考虑了先验概率和似然度的情况下,对决策选项的概率分布进行更新后的结果。它反映了在观测到特定数据后每个决策选项的相对可能性。
7.1.3 似然度(Likelihood)
似然度 描述了在不同决策选项下,观测到某一结果的概率分布。它通常基于观测数据和已知条件概率来计算。
7.1.4 决策规则(Decision Rule)
决策规则是确定如何基于后验概率进行决策的方法。常见的决策规则包括最大后验概率决策、期望效用最大化决策等。
7.1.5 期望损失(Expected Loss)
期望损失(Expected Loss) 是在决策理论和风险管理领域中常用的一个概念。它表示在不同可能性下的损失或成本的平均值,考虑了每种可能性发生的概率。期望损失用于衡量决策或行动的风险和效益,以帮助决策者做出最佳的选择。
7.1.6 条件风险(Conditional Risk)
条件风险 是指在特定条件或情境下可能发生的风险或损失。它是一种局部风险评估,通常基于已知信息和特定的情境来量化风险。
条件风险 考虑了某种特定的情况,例如市场条件、项目条件、环境因素等。条件风险评估有助于确定在特定情况下可能发生的风险,并采取相应的措施来降低这些风险。
7.1.7 总体风险(Aggregate Risk)
总体风险 是指在考虑所有潜在条件和情境下,综合考虑可能发生的所有风险或损失。它是一种全局风险评估,考虑了所有可能性和不确定性。
总体风险 评估通常更全面,因为它不局限于特定条件,而是考虑了所有可能的风险来源,包括市场风险、操作风险、法律风险、战略风险等等。总体风险的评估有助于组织或个人更全面地了解其整体风险暴露,并采取综合性的风险管理措施。
7.1.8 贝叶斯理论
贝叶斯理论,也被称为贝叶斯统计或贝叶斯概率,是一种用于处理不确定性和概率推断的数学框架和统计方法。该理论以英国数学家和统计学家托马斯·贝叶斯(Thomas Bayes)的名字命名,他在18世纪提出了一种概率论的版本,用于解决关于概率和不确定性的问题。
贝叶斯理论的核心思想是通过将先验概率(先前的信念或知识)与新观测数据结合,来计算后验概率(更新后的概率)。
7.1.8 贝叶斯决策论(Bayesian Decision Theory)
贝叶斯决策理论(Bayesian Decision Theory)是一种用于做出决策的概率统计方法,它基于贝叶斯概率理论,旨在最大化决策的期望效用(expected utility)。这一理论的核心思想是将不确定性引入决策过程,并基于先验概率和后验概率来制定决策。
7.1.9 贝叶斯决策步骤
贝叶斯决策通常涉及以下步骤,以帮助决策者做出基于概率和效用的最佳选择:
-
确定决策问题和目标:首先,明确决策的问题是什么,以及您希望达到的目标是什么。确定决策的特定背景和上下文。
-
收集先验信息:收集和整理与决策问题相关的先验信息,这包括任何已知的先验概率、条件概率、关键参数等。这些信息可基于以往经验、专家意见或历史数据来获取。
-
定义决策选项:列出可供选择的不同决策选项,这些选项可能是决策问题的解决方案或策略。
-
计算后验概率:使用贝叶斯定理来计算每个决策选项的后验概率。这需要考虑先验信息和新的观测数据,以更新对每个选项的概率估计。
-
选择决策规则:定义用于选择最佳决策的规则或标准。常见的决策规则包括最大后验概率决策、期望效用最大化决策或其他相关规则。
-
评估期望效用:计算每个决策选项的期望效用,以便比较它们的效益。期望效用通常考虑了不同决策选项的可能结果和相应的效用值。
-
做出决策:基于期望效用或其他选择规则,选择具有最高效用或最佳概率的决策选项作为最终决策。
-
实施并监控:将所选的决策付诸实践,并在实施过程中监测结果。如果有新的观测数据可用,可以随时更新后验概率和重新评估决策。
-
反馈和修正:根据实际结果和反馈信息,可以对决策进行修正和改进,以适应变化的情况和新的信息。
这些步骤构成了贝叶斯决策的一般流程,有助于将不确定性和概率纳入决策过程中,以选择最佳的决策选项。这一方法常用于需要处理不确定性和概率的领域,如金融、医疗、工程和风险管理。
7.2 极大似然估计(Maximum Likelihood Estimation)
7.2.1 频率主义(Frequentist)与概率主义(Bayesian)
频率主义 与 概率主义 是两种不同的概率解释或统计推断方法,它们用于解释和理解随机现象,并对数据进行分析和推断。以下是它们的主要特点和区别:
-
频率主义(Frequentist):
- 频率主义概率是基于经验频率的概率理论。它强调事件的概率是通过重复观测或试验来估计的。
- 在频率主义中,概率被解释为事件发生的相对频率。例如,一个事件的概率可以通过对相同条件下的大量重复试验进行观测来估计。
- 频率主义概率不包含主观元素,它认为概率是客观的、可测量的,并与频率分布相关。
-
概率主义(Bayesian):
- 概率主义概率基于贝叶斯概率理论,它强调概率是一种表示不确定性或信念度量的工具,可以基于先验信息和观测数据来更新。
- 在概率主义中,概率被视为主观度量,反映了个体或系统对事件的信念或不确定性水平。它允许将主观知识或信仰融入概率估计中。
- 概率主义通常使用贝叶斯定理来更新概率分布,将先验概率与似然度相结合以获得后验概率。
主要区别:
- 频率主义将概率视为基于重复观测的频率估计,而概率主义将概率视为主观度量,可以包括个人或系统的信仰和知识。
- 频率主义通常不涉及先验概率,而概率主义强调先验概率的重要性,以帮助更新后验概率。
- 频率主义方法通常更直接,特别适用于大样本情况,而概率主义方法允许在小样本情况下有效地融入先验知识。
频率主义和概率主义在不同领域和问题上都有广泛的应用,选择使用哪种方法通常取决于问题的性质、可用数据和个体或系统的偏好。在实际应用中,有时还会结合两种方法,以充分利用它们的优势。
7.2.2 极大似然估计(Maximum Likelihood Estimation)
极大似然估计(Maximum Likelihood Estimation,简称MLE)是一种用于估计统计模型参数的方法。它基于观测数据,尝试找到使观测数据出现的概率最大化的参数值,从而使模型最有可能生成这些数据。极大似然估计是统计学中最常用的参数估计方法之一。
下面是极大似然估计的一般步骤:
定义统计模型:
-
首先,确定所要估计的参数以及它们的概率分布模型。这通常包括选择合适的概率分布函数,如正态分布、泊松分布等,以描述数据的生成过程。
构建似然函数: -
根据所选的模型和参数,构建似然函数。似然函数是一个关于参数的函数,描述了在给定参数下观测数据的概率分布。
计算似然函数的最大值: -
使用观测数据,计算似然函数在不同参数值下的值。目标是找到能够使似然函数最大化的参数值。
求解最大似然估计: -
通过数学优化方法,如梯度下降或牛顿法,找到能够使似然函数最大化的参数值。这些参数值即为极大似然估计值。
参数估计的性质:
极大似然估计具有一些良好的性质,如一致性、渐进正态性和有效性。这些性质表明,随着样本数量的增加,极大似然估计将趋向于真实参数值,并且在大样本情况下,估计的方差较小。
极大似然估计的应用非常广泛,包括在回归分析、机器学习、贝叶斯统计、生存分析、信号处理和概率模型中。它通常用于从观测数据中学习参数,以拟合模型或进行预测,特别是当我们认为观测数据服从特定的概率分布时,MLE是一个有力的估计方法。
7.2.3 极大似然估计是一种基于频率主义思想的统计方法
极大似然估计是一种基于频率主义思想的统计方法。 它与频率主义概率解释紧密相关,强调了模型参数的估计应基于观测数据的频率分布。MLE 的核心思想是找到使观测数据出现的概率最大化的参数值,从而使模型最有可能生成这些数据。在 MLE 中,概率分布的参数估计是通过最大化似然函数来获得的,而似然函数是关于参数的频率分布。
与之相反,概率主义方法使用贝叶斯推断来估计参数,其中参数的估计是基于主观先验信息和观测数据来更新的。贝叶斯方法涉及到先验概率分布和后验概率分布的计算,与频率主义方法的直接频率估计不同。
因此,MLE 是频率主义思想的一部分,它强调参数估计应基于频率分布和观测数据,而不涉及主观先验信息。
7.2.4 贝叶斯网络与极大似然估计方法之间的关系
贝叶斯网络和极大似然估计方法之间存在密切关系,尤其是在贝叶斯网络参数学习的背景下。贝叶斯网络是一种用于建模概率依赖关系的图模型,而MLE是一种用于估计概率分布参数的常用方法。以下是它们之间的关系:
-
参数学习:
- 贝叶斯网络通常包括节点和有向边,用于表示随机变量之间的概率依赖关系。每个节点都有一个条件概率表(CPT),描述了节点在给定其父节点状态的条件下的条件概率分布。
- MLE是一种用于估计概率分布参数的方法,包括贝叶斯网络中节点的CPT。 MLE的目标是找到使观测数据的似然函数最大化的参数估计。
-
极大似然估计与贝叶斯网络参数学习:
- 在贝叶斯网络中,M步骤通常使用MLE来估计节点的条件概率分布。这就意味着在给定观测数据的情况下,寻找使这些数据的似然函数最大化的CPT值。
- 贝叶斯网络参数学习可以使用不同的先验信息,特别是贝叶斯方法中的先验概率分布,以获得后验概率分布。这就引入了贝叶斯学习的框架,其中参数估计的目标是找到后验分布的模型参数。
-
贝叶斯学习和贝叶斯网络:
- 贝叶斯学习是一种更广泛的框架,它将贝叶斯思想应用于参数估计和不确定性建模。贝叶斯网络是贝叶斯学习的一种具体应用,用于表示和推断概率关系。
- 在贝叶斯网络中,贝叶斯学习的一个重要应用是在参数学习过程中使用贝叶斯方法来引入先验信息,从而提高参数估计的稳健性和泛化性。
贝叶斯网络和MLE方法在参数学习方面有密切关系。贝叶斯网络中的参数估计通常涉及使用MLE来估计节点的条件概率分布,但也可以与贝叶斯方法相结合,以引入先验信息,从而更好地处理不确定性和参数估计的稳健性。
7.3 朴素贝叶斯分类器(Naive Bayes Classifier)与半朴素贝叶斯分类器(Semi-Naive Bayes Classifier)
朴素贝叶斯(Naive Bayes)和半朴素贝叶斯(Semi-Naive Bayes)都是基于贝叶斯定理的分类算法,它们的主要区别在于对特征之间的独立性假设的强度不同。
-
朴素贝叶斯(Naive Bayes):
- 朴素贝叶斯算法做出了一个朴素的假设,即特征之间相互独立,也就是说,给定类别的情况下,每个特征都是相互独立的。这一假设通常被称为"朴素",因为在实际应用中,特征之间往往并不是完全独立的。
- 朴素贝叶斯算法常用于文本分类问题,如垃圾邮件过滤、情感分析等。在文本分类中,每个词或词组被视为一个特征,这种独立性假设可以简化模型的计算和降低数据维度。
-
半朴素贝叶斯(Semi-Naive Bayes):
- 半朴素贝叶斯是对朴素贝叶斯的一种改进,它放松了特征之间的独立性假设,允许一些特征之间的依赖关系。相对于朴素贝叶斯,它更接近实际数据的情况。
- 半朴素贝叶斯算法通常在特征之间存在一定的相关性时表现更好。在某些文本分类任务中,词语之间可能会有一些关联,半朴素贝叶斯可以更好地考虑这些关联。
总之,朴素贝叶斯算法通过强烈的独立性假设来简化问题,适用于特征之间几乎独立的情况。半朴素贝叶斯则在一些特征之间存在一定依赖性的情况下提供了更灵活的建模方式,更接近实际情况。选择哪种算法取决于问题的性质和数据的特点。
7.5 贝叶斯网(Bayesian Network)
贝叶斯网络(Bayesian Network)是一种概率图模型,它用于表示变量之间的概率依赖关系,并可用于概率推理和决策分析。贝叶斯网络是基于概率和图论的方法,被广泛应用于机器学习、人工智能、数据分析和决策支持系统中。
贝叶斯网络的主要组成部分包括:
-
节点(Nodes):每个节点代表一个随机变量或事件,可以是离散的或连续的。节点之间的连接表示这些变量之间的概率依赖关系。
-
边缘(Edges):边缘表示节点之间的概率依赖关系。有向边缘表示因果关系,即一个节点的状态会影响另一个节点的状态。
-
条件概率分布(Conditional Probability Distribution,CPD):每个节点都有一个条件概率分布,描述了该节点在给定其父节点的状态下的条件概率。
-
网络结构:贝叶斯网络的拓扑结构由节点和边缘组成,描述了变量之间的依赖关系。
使用贝叶斯网络,可以进行以下任务:
-
概率推理:根据已知的观测数据和贝叶斯网络的结构,可以计算未观测变量的后验概率分布,以进行概率推理。
-
预测:可以使用贝叶斯网络进行概率预测,例如预测未来事件的发生概率。
-
诊断:在医学诊断、故障诊断等领域,贝叶斯网络可以帮助确定可能的原因。
-
决策支持:贝叶斯网络可用于决策分析,帮助选择最佳决策方案。
-
数据生成:可以使用贝叶斯网络生成符合特定条件的数据样本。
贝叶斯网络是一种强大的建模工具,特别适用于处理不确定性和复杂依赖关系的问题。在实际应用中,使用各种工具和库,如PyMC3、Stan、OpenBUGS和AgenaRisk等,可以方便地构建和分析贝叶斯网络模型。
7.5.1 结构
贝叶斯网络结构有效地表达了属性间的条件独立性。如前面所述,贝叶斯网络的结构由两个主要组件组成:节点(Nodes)和有向边(Directed Edges)。贝叶斯网络是一个有向无环图(DAG),其中节点表示随机变量,有向边表示这些变量之间的概率依赖关系。以下是一些关于贝叶斯网络结构的重要信息:
-
节点(Nodes):每个节点代表一个随机变量或一个事件,这些变量可以是离散的或连续的。节点可以表示各种事物,例如天气、疾病状态、传感器测量结果等。
-
有向边(Directed Edges):有向边用于表示节点之间的因果关系或条件独立性。如果从节点A到节点B有一条有向边,那么A被称为B的父节点,意味着A的状态会影响B的状态。这种有向关系有助于描述概率依赖性。
-
条件独立性:一个贝叶斯网络的关键特点是它可以表示条件独立性。如果在给定其父节点的情况下,一个节点与其他节点条件独立,那么这种条件独立性关系可以通过网络的结构来表示。
-
条件概率表(Conditional Probability Tables,CPTs):每个节点都有一个条件概率表,描述了该节点在不同父节点状态下的条件概率分布。这些表用于量化节点之间的概率依赖关系。
-
生成模型:贝叶斯网络可以用来生成随机样本,从而模拟随机事件的发生。这是因为网络的结构和CPTs可以用来计算联合概率分布,从而生成数据。
7.5.2 学习
贝叶斯网络的学习过程是指从数据中推导出贝叶斯网络的结构和参数的过程。学习贝叶斯网络可以分为两个主要方面:结构学习和参数学习。
-
结构学习(Structure Learning):
- 结构学习的目标是确定网络中节点之间的有向边的连接关系,即确定贝叶斯网络的拓扑结构。
- 常用的结构学习方法包括:贝叶斯信息准则(Bayesian Information Criterion, BIC)、最大似然估计(Maximum Likelihood Estimation, MLE)、约束优化方法(如禁忌搜索、遗传算法等)和基于数据的方法(如概率独立测试)。
- 结构学习方法通常基于数据集,通过评估不同的网络结构来选择最佳拓扑结构,以最好地拟合数据。
-
参数学习(Parameter Learning):
- 参数学习的目标是确定每个节点的条件概率表(CPT)或概率密度函数。这些表描述了节点在给定其父节点状态的情况下的条件概率分布。
- 参数学习通常通过使用训练数据集来估计每个节点的CPT。估计方法包括频率估计、最大似然估计、贝叶斯估计等。
- 对于离散变量,通常使用频率计数来估计条件概率;对于连续变量,可以使用参数化分布(如高斯分布)来拟合数据,然后估计分布的参数。
整个学习过程可以总结如下:
-
收集数据:首先,需要获取一个包含相关随机变量的数据集,以便用于学习贝叶斯网络。
-
结构学习:选择适当的结构学习方法,该方法将尝试识别节点之间的有向边的连接关系。这可以通过评估不同的网络结构以找到最优结构。
-
参数学习:确定每个节点的条件概率表或概率密度函数,这需要使用训练数据来估计参数。
-
验证和改进:验证学习得到的网络的性能,通常使用交叉验证等技术来评估模型的质量。如果需要,可以根据性能来进一步改进网络结构和参数。
学习贝叶斯网络的复杂性取决于数据集的规模和问题的复杂性。在大型数据集和复杂问题的情况下,结构学习和参数学习可能需要高度计算密集的方法。
7.5.3 推断
贝叶斯网络的推断过程是指根据已知信息和贝叶斯网络的结构与参数来估计网络中未知随机变量的概率分布或条件概率。推断是贝叶斯网络在实际应用中的关键部分,用于回答关于未来事件或隐含变量的概率性问题。以下是贝叶斯网络的推断过程的一般步骤:
-
观测数据(Evidence):在进行推断之前,需要确定已知的观测数据或证据。这些观测数据通常是已知的随机变量的值,它们将用于推断未知的变量。
-
选择查询变量(Query Variables):确定您想要推断的未知变量。这些变量可以是网络中的任何节点,你可以问关于它们的概率问题,如条件概率、边际概率等。
-
推断算法的选择:选择适当的推断算法,根据网络的结构和问题的复杂性。常见的推断算法包括:
- 采样方法(如马尔可夫链蒙特卡罗采样,Gibbs采样):这些方法通过生成大量样本来估计目标变量的概率分布。
- 精确推断方法(如变量消去、信念传播):这些方法用于计算概率分布的精确解,但在复杂网络中可能面临计算复杂性问题。
- 近似推断方法(如变分推断、期望传播):这些方法提供了近似解,通常在大型或高度复杂的网络中更高效。
-
推断过程:
- 对于精确推断方法,计算目标变量的概率分布,通常涉及概率传递和条件概率计算。
- 对于采样方法,生成大量样本并计算目标变量的统计属性,例如均值和方差。
-
结果解释:解释推断结果,回答与查询变量相关的概率问题。这可能包括计算条件概率、边际概率、预测未来事件等。
-
可视化和应用:可视化推断结果以便更好地理解网络中变量之间的关系,并将推断结果应用于实际决策制定或问题解决中。
需要注意的是,贝叶斯网络的推断过程可能会受到网络结构的复杂性和变量的数量影响,以及所选择的推断算法的计算效率。在某些情况下,精确推断可能过于昂贵,需要使用近似方法,而在其他情况下,精确推断可能是可行的。选择适当的推断方法取决于具体的问题和计算资源。
7.5.4 吉布斯采样算法(ibbs sampling)
贝叶斯网的近似推断常使用吉布斯采样来完成。
吉布斯采样(Gibbs Sampling)是一种马尔可夫链蒙特卡罗(MCMC)方法,用于从多维概率分布中抽样。它通常用于处理高维联合分布中的条件概率问题,特别是在贝叶斯网络、潜在变量模型和概率图模型等领域中。
吉布斯采样的核心思想是通过依次更新每个变量的值,每次根据其他变量的当前值来抽样一个变量的新值。这一过程在马尔可夫链上进行,最终收敛到平稳分布,从而得到联合分布的样本。
下面是吉布斯采样的基本步骤:
-
初始化:选择一个初始状态,即每个变量的初值。
-
迭代:重复以下步骤直到满足收敛条件:
- 对于每个变量,依次更新它的值,将其看作是其他变量的条件分布。这是吉布斯采样的核心步骤。
- 更新后的值成为新的样本。
-
满足收敛条件:通常,可以设置一个停止准则,例如固定的迭代次数、样本数量或平稳状态的收敛检测方法。
吉布斯采样的关键是在每个变量更新时,将其看作是其他变量的条件分布,这可以是通过概率分布的边缘化来实现。这样,吉布斯采样在每次迭代中依次更新每个变量,然后循环进行,从而逐渐逼近平稳分布。
吉布斯采样的应用包括:
- 在贝叶斯网络中进行概率推断。
- 在潜在变量模型(如隐马尔可夫模型、潜在狄利克雷分布)中进行参数估计和抽样。
- 在概率图模型中进行采样,如马尔可夫随机场。
吉布斯采样是一种强大的采样方法,但需要小心处理收敛问题和初始状态选择。此外,吉布斯采样的效率受到变量的排序和条件分布的选择影响,因此在实际应用中需要谨慎考虑这些因素。
7.6 EM (Expectation-Maximization)算法
7.6.1 EM 算法概述
期望最大化(Expectation-Maximization,EM) 算法是一种迭代优化算法,用于处理包含隐含变量的概率模型,特别是在统计建模和机器学习中的概率估计问题中广泛应用。EM算法的主要目标是通过迭代寻找最大似然估计(Maximum Likelihood Estimation,MLE)或最大后验估计(Maximum A Posteriori,MAP)的参数,特别是在存在隐含变量时。
EM算法通常用于以下情况:
-
数据不完整:当数据集包含隐含变量或缺失数据时,EM算法可以用来估计概率模型的参数。
-
概率模型:EM算法通常与概率模型(如高斯混合模型、隐马尔可夫模型等)结合使用,用于估计这些模型的参数。
EM算法的基本思想 可以分为两个步骤:E步骤(Expectation Step)和M步骤(Maximization Step)。
-
E步骤(Expectation Step):
- 在E步骤中,根据当前参数的估计值,计算隐含变量的条件概率分布(后验分布)。这个分布描述了在给定观测数据和当前参数下,每个隐含变量的可能状态。
- E步骤的目标是计算期望值,因此得名"期望"最大化。
-
M步骤(Maximization Step):
- 在M步骤中,使用E步骤得到的隐含变量的期望值,来更新模型参数。这通常涉及最大化似然函数或其变种,以寻找新的参数估计值。
- M步骤的目标是"最大化"似然估计或MAP估计。
EM算法将这两个步骤交替进行多次迭代,直到参数的变化足够小,或者满足收敛条件。最终,EM算法收敛到一个局部最优解,这个解使似然函数最大化。
EM 算法是一种用于估计包含隐含变量的概率模型的参数的迭代算法,可看作一种非梯度优化方法,它通过交替进行期望步骤和最大化步骤,寻找似然函数的最大值。EM算法在很多领域中都有应用,包括聚类、密度估计、隐马尔可夫模型、高斯混合模型等。
7.6.2 EM 算法与贝叶斯网络
贝叶斯网络和EM算法可以在概率建模和参数估计问题中相互结合使用。EM算法可用于估计贝叶斯网络的参数,尤其是在存在隐含变量或观测数据不完整的情况下。这种结合可以帮助更好地理解和利用复杂的概率模型。
贝叶斯网络与 EM 算法的关系包括:
- 贝叶斯网络通常包括节点和有向边,以表示随机变量之间的概率依赖关系。每个节点都有一个条件概率表(CPT),描述节点在给定其父节点状态的条件下的条件概率分布。
- EM算法可以用于估计贝叶斯网络中的参数,即节点的CPT。在这种情况下,EM算法通常被称为"结构学习",其目标是通过最大化观测数据的似然函数来找到最佳参数估计。
7.7 总结
贝叶斯分类器是一种基于贝叶斯定理的概率分类算法,用于将输入数据分配到不同的类别。以下是关于贝叶斯分类器的主要特点和工作原理的总结:
-
基于概率:
- 贝叶斯分类器基于贝叶斯定理,利用输入数据的特征和类别之间的条件概率来进行分类。
- 它对不同类别的概率分布进行建模,然后使用贝叶斯定理来计算给定数据点的后验概率,以确定最有可能的类别。
-
独立性假设:
- 贝叶斯分类器通常使用朴素贝叶斯分类器,其中特征之间被假定为条件独立。尽管这一假设在现实中不一定成立,但它简化了模型,使其计算更加高效。
-
训练和测试:
- 在训练阶段,贝叶斯分类器学习不同类别的条件概率分布,即学习类别之间的模型参数。
- 在测试阶段,贝叶斯分类器使用已知的条件概率模型来为新的输入数据点分配类别。
-
适用于多类别问题:
- 贝叶斯分类器适用于多类别分类问题,它可以将数据分为多个类别,而不仅仅是二分类问题。
-
处理缺失数据:
- 贝叶斯分类器具有处理缺失数据的能力,因为它使用条件概率进行分类,即使某些特征值缺失也可以进行分类。
-
朴素贝叶斯和变种:
- 朴素贝叶斯是最常见的贝叶斯分类器,但还有其他变种,如多项式贝叶斯、高斯贝叶斯等,适用于不同类型的数据。
-
优点:
- 简单且高效,适用于大规模数据集。
- 适用于多类别分类问题。
- 对于小样本数据和高维数据也有良好的性能。
-
缺点:
- 朴素贝叶斯的独立性假设在某些情况下可能不成立,导致分类性能下降。
- 不能处理类别间的复杂依赖关系。
- 对于不平衡数据集可能表现不佳。
Smileyan
2023.11.04 23:10
相关文章:
—— 第七章 贝叶斯分类器)
西瓜书读书笔记整理(七)—— 第七章 贝叶斯分类器
第七章 贝叶斯分类器 7.1 贝叶斯决策论(Bayesian Decision Theory)7.1.1 先验概率(Prior Probability)7.1.2 后验概率(Posterior Probability)7.1.3 似然度(Likelihood)7.1.4 决策规…...

C#WPF嵌套布局实例
本文演示C#WPF嵌套布局实例。演示了不同布局的简单用法,便于快速应用和掌握。 <Windowx:Class="LayoutDemo.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/x…...
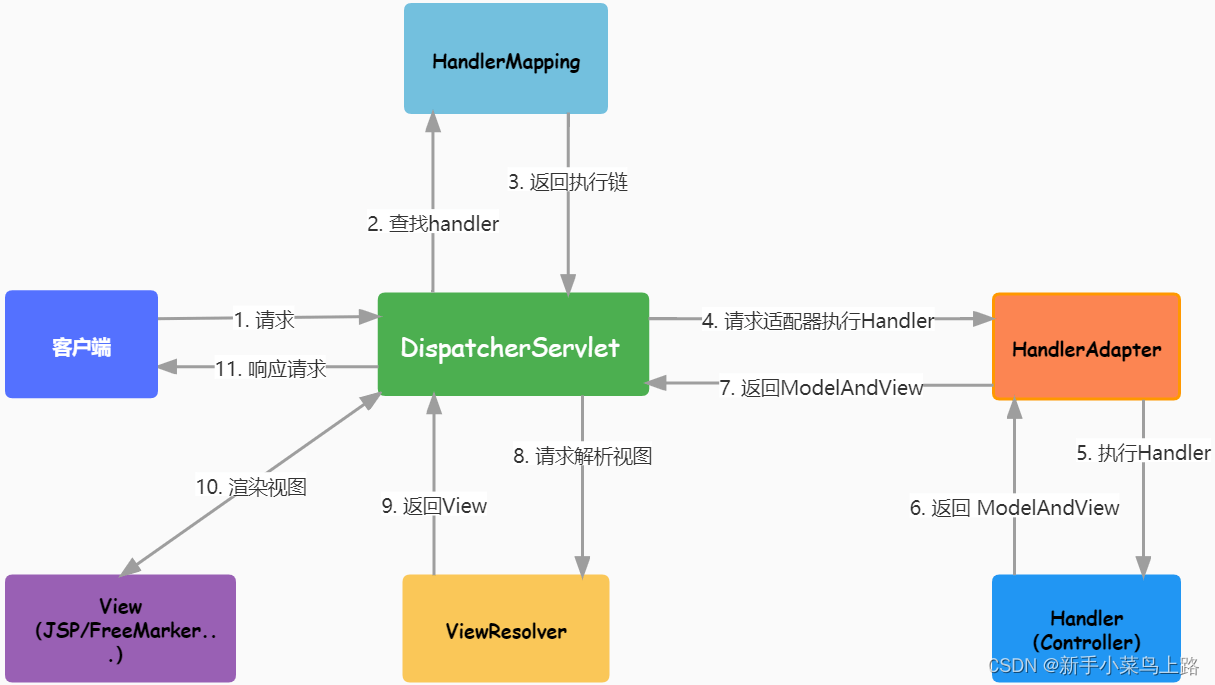
Spring和SpringMVC总结
一、Spring IoC(Inversion of Control)中文名称:控制反转(对象的创建交给Spring管理)。DI(dependency injection )依赖注入。容器(Container):放置所有被管理的对象。beans:容器中所有被管理的对…...
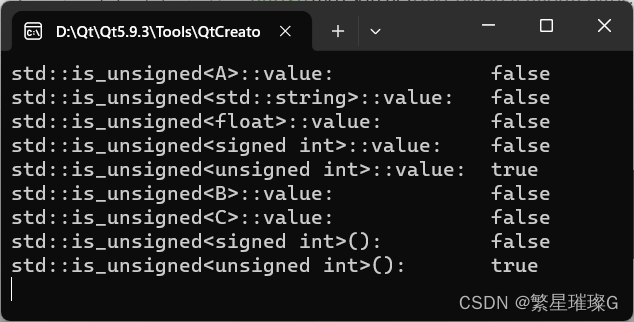
C++标准模板(STL)- 类型支持 (类型属性,is_abstract,is_signed,is_unsigned)
类型特性 类型特性定义一个编译时基于模板的结构,以查询或修改类型的属性。 试图特化定义于 <type_traits> 头文件的模板导致未定义行为,除了 std::common_type 可依照其所描述特化。 定义于<type_traits>头文件的模板可以用不完整类型实例…...

前端复制带上版权信息
前端复制带上版权信息 当用户复制内容时,自动添加版权信息。 HTML内容 <body><h1 inputmode"text">复制我</h1> </body>Js内容 document.addEventListener("copy", (event) > {event.preventDefault(); // 阻止…...
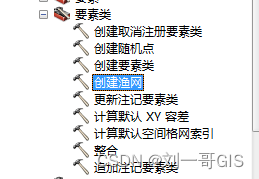
【ArcGIS微课1000例】0077:ArcGIS生成经纬网(shp格式)
使用ArcGIS制图的时候,可以很方便的生成经纬网、方里网及参考格网,但是在需要shp格式的经纬网,进一步在南方cass中使用经纬网的时候,就需要单独生成了。 如下图所示为全球大陆矢量数据,我们基于该数据来生成全球指定间距的经纬网数据。 在ArcGIS中,生成经纬网和方里网均…...
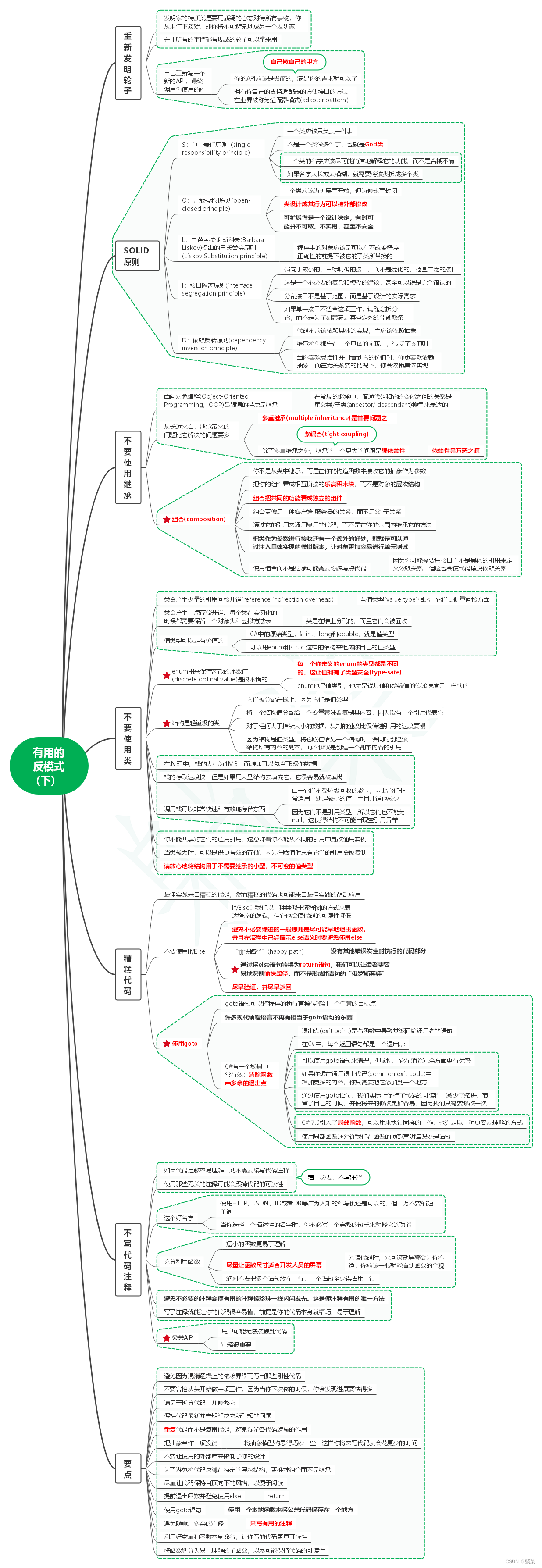
读程序员的制胜技笔记04_有用的反模式(下)
1. 重新发明轮子 1.1. 发明家的特质就是要用质疑的心态对待所有事物,你从未停下质疑,那你将不可避免地成为一个发明家 1.2. 并非所有的事情都有现成的轮子可以拿来用 1.3. 自己重新写一个新的API,最终调用你使用的库 1.3.1. 你的API应该是…...
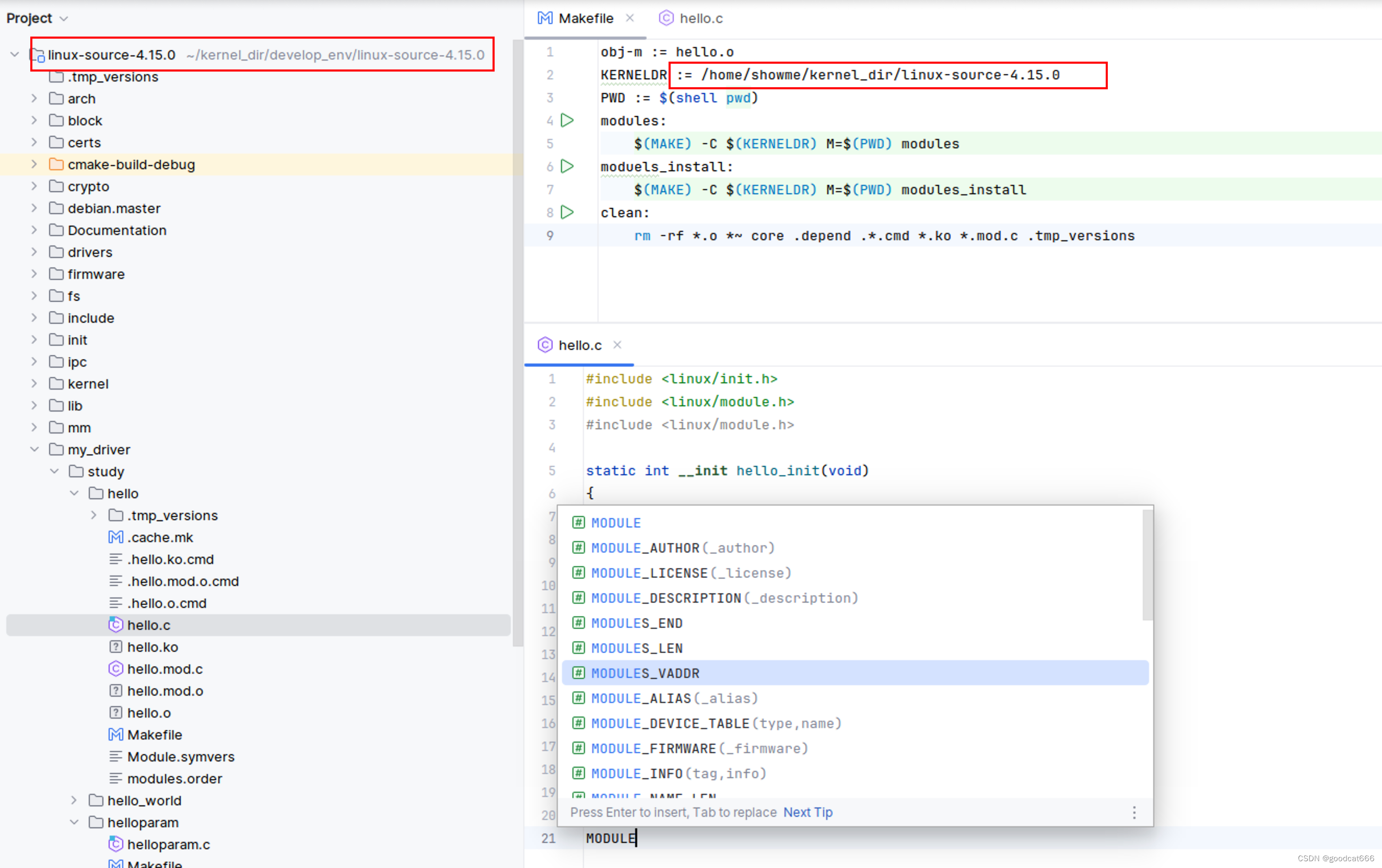
linux驱动开发环境搭建
使用的是parallel 创建的ubuntu 16.04 ubuntu20.04虚拟机 源码准备 # 先查看本机版本 $ uname -r 5.15.0-86-generic# 搜索相关源码 $ sudo apt-cache search linux-source [sudo] password for showme: linux-source - Linux kernel source with Ubuntu patches linux-sourc…...

Qt利用VCPKG和CMake和OpenCV和Tesseract实现中英文OCR
文章目录 1. 开发平台2. 下载文件2.1 下载安装 OpenCV 库2.2 下载安装 Tesseract-OCR库2.3 下载训练好的语言包 3. CMakeLists.txt 内容4. Main.cpp4.1 中英文混合OCR 5. 在Qt Creator 中设置 CMake vcpkg5.1 在初始化配置文件里修改5.2 在构建配置里修改 说明:在Q…...
Day20力扣打卡
打卡记录 数组中两个数的最大异或值(位运算) 链接 二进制位上从高位向低位进行模拟,看数组中是否有满足此情况的数字。具体题解 class Solution { public:int findMaximumXOR(vector<int>& nums) {int mx *max_element(nums.be…...
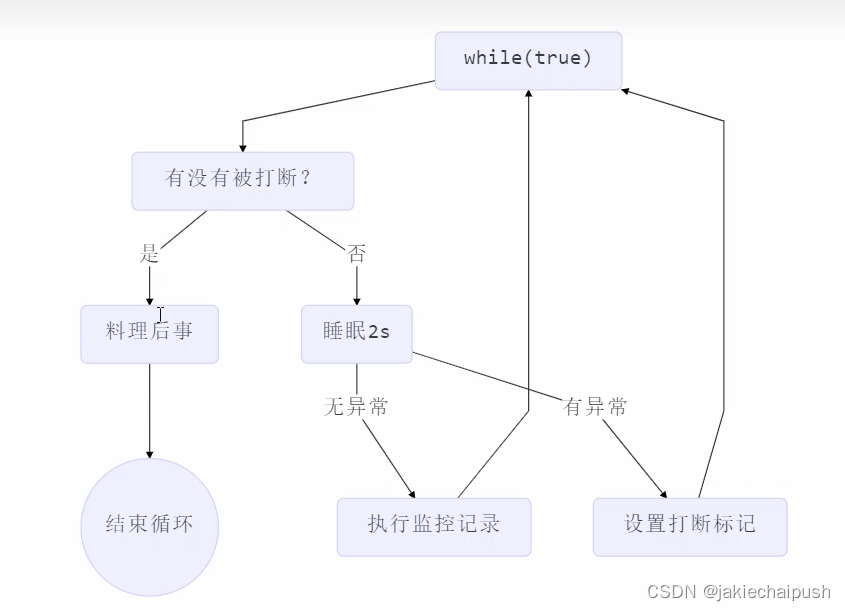
设计模式之两阶段终止模式
文章目录 1. 简介 2. 常见思路3. 代码实战 1. 简介 两阶段终止模式(Two-Phase Termination Pattern)是一种软件设计模式,用于管理线程或进程的生命周期。它包括两个阶段:第一阶段是准备阶段,该阶段用于准备线程或进程…...
Dubbo捕获自定义异常
一.问题描述 Dubbo远程服务提供者抛出的自定义异常无法被消费方正常捕获,消费方捕获的自定义异常全部变成RuntimeException,使用起来很不方便。 二.原因分析 相关源码 /** Licensed to the Apache Software Foundation (ASF) under one or more* con…...
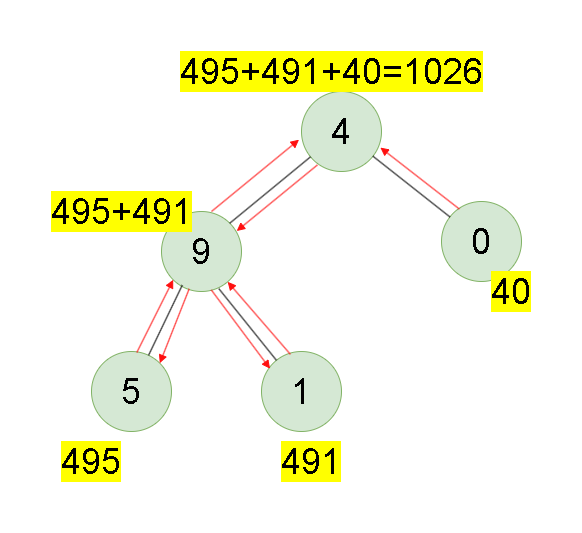
Leetcode刷题详解——求根节点到叶节点数字之和
1. 题目链接:129. 求根节点到叶节点数字之和 2. 题目描述: 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1…...

emq集群配置nginx做负载均衡
emq集群配置nginx做负载均衡 创建 EMQ X 节点集群 emqx 集群搭建 例如: 节点IP 地址emqx192.168.1.17192.168.1.17emqx192.168.1.18192.168.1.18emqx192.168.1.19192.168.1.19 配置 /etc/nginx/nginx.conf mqtt集群搭建并使用nginx做负载均衡_亲测得结论 示例: vim /et…...

【JAVA学习笔记】60 - 坦克大战1.0-绘图坐标体系、事件处理机制
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter16/src/com/yinhai 绘图坐标体系 一、基本介绍 下图说明了Java坐标系。坐标原点位于左上角,以像素为单位。在Java坐标系中,第一个是x坐标,表示当前位置为…...

Android13 安装谷歌GMS导致打开蓝牙失败解决方法
Android13 安装谷歌GMS导致打开蓝牙失败解决方法 文章目录 Android13 安装谷歌GMS导致打开蓝牙失败解决方法一、前言二、解决方法1、简单的解决方法2、添加属性和日志解决 三、分析1、查看异常日志2、 查看蓝牙相关日志 四、总结1、Android13 安装谷歌GMS导致打开蓝牙失败具体原…...

独创改进 | RT-DETR 引入双向级联特征融合结构 RepBi-PAN | 附手绘结构图原图
本专栏内容均为博主独家全网首发,未经授权,任何形式的复制、转载、洗稿或传播行为均属违法侵权行为,一经发现将采取法律手段维护合法权益。我们对所有未经授权传播行为保留追究责任的权利。请尊重原创,支持创作者的努力,共同维护网络知识产权。 文章目录 YOLOv6贡献RepBi-…...
Ubuntu下安装vscode,并解决终端打不开vscode的问题
Visual Studio Code安装 1,使用 apt 安装 Visual Studio Code 在官方的微软 Apt 源仓库中可用。按照下面的步骤进行即可: 以 sudo 用户身份运行下面的命令,更新软件包索引,并且安装依赖软件: sudo apt update sud…...
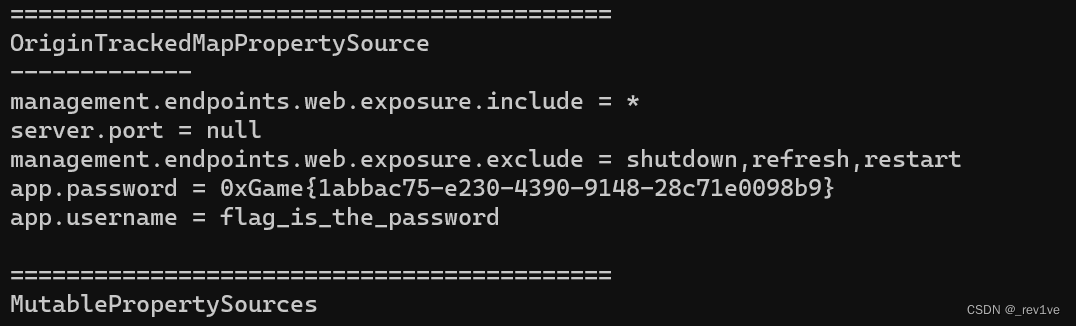
Spring Boot Actuator 漏洞利用
文章目录 前言敏感信息泄露env 泄露配置信息trace 泄露用户请求信息mappings 泄露路由信息heapdump泄露堆栈信息 前言 spring对应两个版本,分别是Spring Boot 2.x和Spring Boot 1.x,因此后面漏洞利用的payload也会有所不同 敏感信息泄露 env 泄露配置信…...

acwing算法基础之数据结构--trie算法
目录 1 基础知识2 模板3 工程化 1 基础知识 trie树算法,也叫作字典树算法。 用处:用来高效存储和查找字符串集合的数据结构。 (一) 定义变量。 const int N 1e5 10; int son[N][26], cnt[N], idx; char str[N];(二…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
