02 线性组合、张成的空间与基
线性组合、张成的空间与基
- 基向量
- 缩放向量并相加
- 给定向量张成的空间
- 线性相关与线性无关
- 空间的基
这是关于3Blue1Brown "线性代数的本质"的学习笔记。
基向量
当看到一对描述向量的数时,比如[3,-2]时,把这对数中的每个数(坐标)看作一个标量,表示它们如何对坐标系上各轴单位向量 i ⃗ \vec{i} i和 j ⃗ \vec{j} j进行拉伸或压缩。

单位向量 i ⃗ \vec{i} i和 j ⃗ \vec{j} j就是这个2维坐标系 x y xy xy的基向量。
缩放向量并相加

从这个角度看,向量[3,-2]实际上是两个经过缩放的向量之和。
每当我们用数字对表示一个向量时,它都依赖于我们正在使用的基向量。

两个数乘向量之和被称为这两个向量的线性组合。如果让两个向量的线性组合中的标量 a , b a,b a,b同时自由变化,大多数情况下能到达2维平面内的每一个点。只有两种情况下例外,一是这两个向量共线,二是这两个向量是零向量。
给定向量张成的空间
所有可以表示为两个给定向量线性组合的向量的集合,被称为两个给定向量张成的空间。



- 如果第三个向量恰好落在前面两个向量张成的平面上,它们张成的空间并不会发生变化
- 如果第三个向量没有在前面两个向量张成的平面上,它们张成的空间构成整个3维空间
可以想象,第三个向量将前面两个向量张成的平面沿它的方向来回移动,从而扫过整个3维空间。
线性相关与线性无关
两个给定向量共线,或者第三个向量恰好落在前面两个向量张成的平面上,这两种情况下,也就是一组向量中至少有一个是多余的,对张成的空间没有贡献,这时候就称它们是线性相关(Linearly dependent)的。另一种说法就是,一组向量中,有向量可以表示为其他向量的线性组合,那它们就是线性相关的;因为这个向量已经落在了其他向量张成的空间之中。
另一方面,如果一组向量中的所有向量都给张成的空间增添了新的维度,它们就被称为是线性无关的。
空间的基
空间的一组基的严格定义:张成该空间的一个线性无关向量的集合。即:向量空间的一组基是张成改空间的一个线性无关向量集。
相关文章:

02 线性组合、张成的空间与基
线性组合、张成的空间与基 基向量缩放向量并相加给定向量张成的空间线性相关与线性无关空间的基 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 基向量 当看到一对描述向量的数时,比如[3,-2]时,把这对数中的每个数(坐标&…...
解析mfc100u.dll文件丢失的修复方法,快速解决mfc100u.dll问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中最常见的就是“缺少某个文件”的错误。最近,我也遇到了一个这样的问题,那就是“mfc100u.dll丢失”。这个问题可能会导致某些应用程序无法正常运行,给我们带来困扰。…...
免费外文文献检索网站,你一定要知道
01. Sci-Hub 网址链接:https://tool.yovisun.com/scihub/ Sci-hub是一个可以无限搜索、查阅和下载大量优质论文的数据库。其优点在于可以免费下载论文文献。 使用方法: 在Sci—hub搜索栏中粘贴所需文献的网址或者DOI,然后点击右侧的open即可…...

大数据毕业设计选题推荐-收视点播数据分析-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...
传智杯-21算法赛初赛B组题目详细解法解析-AB题(C/C++、Python、Java)
🚀 欢迎来到 ACM 算法题库专栏 🚀 在ACM算法题库专栏,热情推崇算法之美,精心整理了各类比赛题目的详细解法,包括但不限于ICPC、CCPC、蓝桥杯、LeetCode周赛、传智杯等等。无论您是刚刚踏入算法领域,还是经验丰富的竞赛选手,这里都是提升技能和知识的理想之地。 ✨ 经典…...

post给后端传递数组和多个参数
这是前端的数据结构 data() {return {loading: false,inputForm: {id: ${gridProject.id},gridName: ,gridId: ,projectName: ,projectId: ,type: },data: [],value: []}}, 其中 gridId 和 type 是单个参数 , value 是个数组,注意 这里data中的value[]不要直接给后…...
音频修复增强软件iZotope RX 10 mac中文特点
iZotope RX 10 mac是一款音频修复和增强软件。 iZotope RX 10 mac主要特点 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。 音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等处…...

【面试】虚拟机栈面试题
目录 一、举例栈溢出的情况二、调整栈大小,能保证不出现溢出吗?三、分配的栈内存越大越好吗?四、垃圾回收是否会涉及到虚拟机栈?五、方法中定义的局部变量是否存在线程安全问题?5.1 说明5.2 代码示例 一、举例栈溢出的…...

白话熵增定律
白话熵增定律 热力学中的熵增定律 熵是指一个系统的混乱程度的度量,是热力学中的一个系统的属性。熵增定律是指一个封闭的系统随着时间的发展,在朝平衡状态发展时,其熵会增加,即其越来越混乱。 对于一个房间,如果经常…...
End-to-end people detection in crowded scenes)
(论文阅读14/100)End-to-end people detection in crowded scenes
文献阅读笔记 简介 题目 End-to-end people detection in crowded scenes 作者 Russell Stewart, Mykhaylo Andriluka 原文链接 https://arxiv.org/pdf/1506.04878.pdf 关键词 Null 研究问题 当前的人员检测器要么以滑动窗口的方式扫描图像,要么对一组离…...

Go的错误处理
什么是错误? 错误表示程序中发生的任何异常情况。假设我们正在尝试打开一个文件,但该文件在文件系统中不存在。这是一种异常情况,表示为错误。 Go 中的错误是普通的旧值。就像任何其他内置类型(例如 int、float64 等)…...

云原生相关概念
云计算 指托管在外部数据中心并按使用量付费提供给用户的软件基础设施。公司不必为昂贵的服务器付费并进行维护。相反,他们可以使用云提供商提供的按需云原生服务,例如存储、数据库和分析。 云原生 是在 云计算环境 中构建、部署和管理现代应用程序的…...
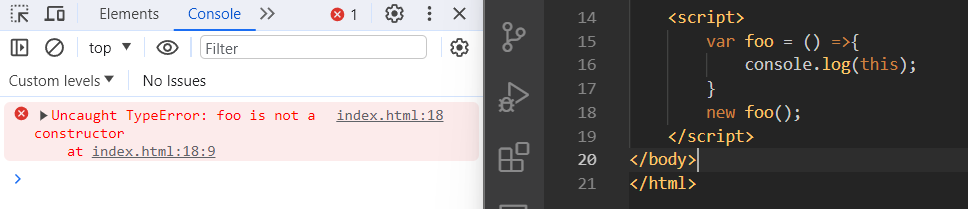
【JS】this指向
一、this指向的四种规则 1.默认绑定规则 默认指向:指向window 独立调用:指向window 对象指向,比较的是引用地址。 console.log(this window); //true console.log({} {}); //false //函数的独立调用 function test(){console.lo…...
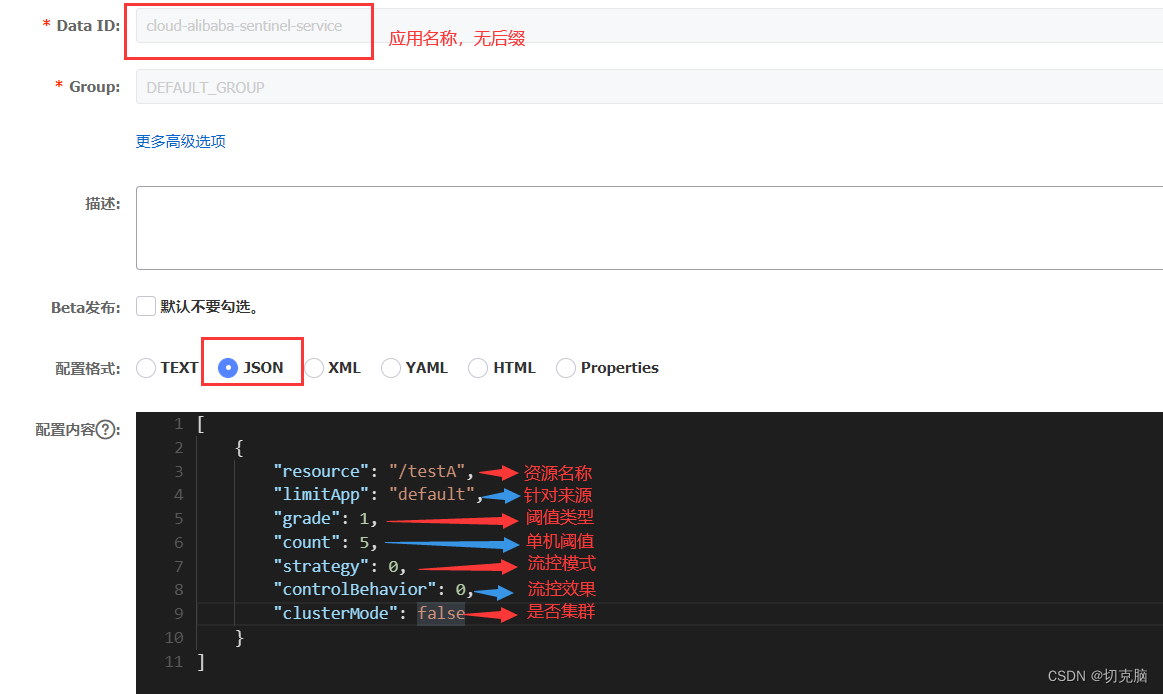
SpringCloud Alibaba Demo(Nacos,OpenFeign,Gatway,Sentinel)
开源地址: ma/springcloud-alibaba-demo 简介 参考:https://www.cnblogs.com/zys2019/p/12682628.html SpringBoot、SpringCloud 、SpringCloud Alibaba 以及各种组件存在版本对应关系。可参考下面 版本对应 项目前期准备 启动nacos. ./startup.c…...
基于nodejs+vue畅听校园点歌系统的设计与实现
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
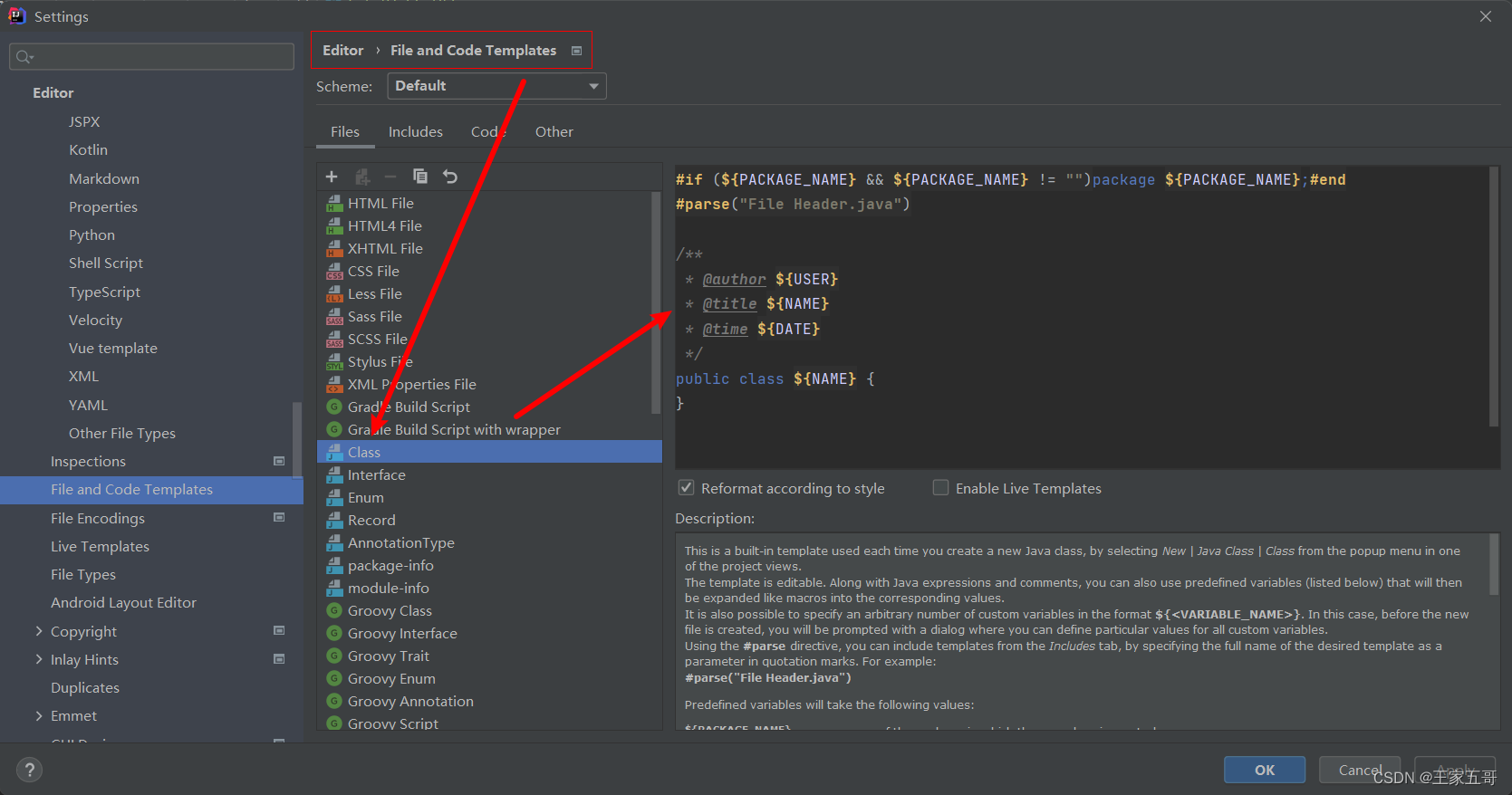
IDEA 设置代码注释模板
功能简介: 每次看别人代码时,面对毫无注释的类,除了头大还是头大, 以下提供了一种代码类注释模板 新建java类的时候,自动增加类注释,养成代码开发好习惯 效果展示: 代码模板: #if (…...

emoji对齐 特殊字符对齐 文本对齐
emoji如何对齐 特殊字符如何对齐 高级文本对齐 问题引出 我们在程序打印输出时,如何我们所输出的字符中包含emoji文本,或者其它特殊的字符文本,则我们的打印对齐效果将出现错位。以下代码复现了这一效果(tips: 马老师…...

Selenium Python 中的动作链
Selenium 是一个用于自动化的独立的基于 Web 的工具。 它是任何人都可以使用的开源工具。 与Python语言结合使用该工具进行测试。 操作链是 Selenium 的基本组成部分,提供了一种管理低级交互的方法,例如按键、鼠标移动、鼠标按钮操作以及与上下文菜单的…...
OceanBase:03-集群部署
目录 一、集群规划 二、配置要求 三、部署前配置 1.配置 limits.conf 2.配置 sysctl.conf 3.关闭防火墙 4.关闭 SELinux 5.创建数据目录,修改文件所有者信息 6.设置无密码 SSH 登录 7.安装jdk 四、解压执行安装 五、集群部署 1.OBD命令行部署 2. OBD白…...

PTA: 矩阵的乘法运算
矩阵的乘法运算 题目输入格式输出格式输入样例输出样例 代码 题目 线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时&…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
