03 矩阵与线性变换
矩阵与线性变换
- 线性变换
- 如何用数值描述线性变换
- 特殊的线性变换
- 反过来看
- 总结
这是关于3Blue1Brown "线性代数的本质"的学习笔记。
线性变换
如果一个变换具有以下两个性质,我们就称它是线性的:
- 一是直线在变换后仍然保持为直线
- 二是原点必须保持固定
总的来说,线性变换是“保持网格线平行且等距分布”的变换
如何用数值描述线性变换
只需记录两个基向量 i ⃗ \vec{i} i和 j ⃗ \vec{j} j变换后的位置。可以用 i ⃗ \vec{i} i和 j ⃗ \vec{j} j变换后的位置,推断任意向量出变换后的位置。


如图2所示,假设 i ⃗ \vec{i} i和 j ⃗ \vec{j} j变换后分别为 [ 1 , − 2 ] T [1, -2]^{T} [1,−2]T和 [ 3 , 0 ] T [3, 0]^{T} [3,0]T,则任意向量 [ x , y ] T [x, y]^{T} [x,y]T的变换结果如图2所示。
即:一个二维线性变换仅由四个数字完全确定,变换后 i ⃗ \vec{i} i的两个坐标和变换后 j ⃗ \vec{j} j的两个坐标。把这两组坐标写入一个矩阵中,如图3所示。

这个矩阵的第一列就是变换后 i ⃗ \vec{i} i的两个坐标,第二列就是变换后 j ⃗ \vec{j} j的两个坐标。


更一般的情况,如图4所示。
把第一列 [ a , c ] T [a,c]^{T} [a,c]T看作是变换后的第一个基向量,把第二列 [ b , d ] T [b,d]^{T} [b,d]T看作是变换后的第二个基向量,则任意向量 [ x , y ] T [x, y]^{T} [x,y]T的变换过程和结果如图4所示。
矩阵的列就是变换后的基向量,矩阵向量乘法就可以看作它们的线性组合。
特殊的线性变换
坐标系 x y x y xy的基向量分别为 i ⃗ \vec{i} i(绿色箭头)、 j ⃗ \vec{j} j(红色箭头)。我们将这个坐标系 x y x y xy逆时针旋转90°,这样, i ⃗ \vec{i} i落在了坐标 ( 0 , 1 ) (0,1) (0,1)上, j ⃗ \vec{j} j落在了坐标 ( − 1 , 0 ) (-1,0) (−1,0)上,如图5所示。

这样,任意向量 [ x , y ] T [x, y]^{T} [x,y]T旋转90°之后的结果都可以利用这个矩阵计算出来。
还有一种特殊的线性变换是“剪切”。如图6所示,变换后 i ⃗ \vec{i} i不变, j ⃗ \vec{j} j落在了坐标 ( 1 , 1 ) (1,1) (1,1)上。
反过来看
给定一个变换矩阵 [ 1 3 2 1 ] \begin{bmatrix} \ 1 & 3 \\ \ 2 & 1 \\ \end{bmatrix} [ 1 231]
这就相当于 i ⃗ \vec{i} i变换后落在(1,2)上, j ⃗ \vec{j} j变换后落在(3,1)上,空间其他部分随二者一起移动,以保持网格线平行且等距分布。如图7所示。

如果变换后的 i ⃗ \vec{i} i和 j ⃗ \vec{j} j是线性相关的,如图8所示,变换后的 i ⃗ \vec{i} i和 j ⃗ \vec{j} j在一条直线上。

总结
线性变换是操纵空间的一种手段,它保持网格线平行且等距分布,并保持原点不动。
这种变换只需要几个数字就能描述清楚,这些数字就是变换后基向量的坐标,以这些坐标为列所构成的矩阵为我们提供了一种描述线性变换的语言,而矩阵向量乘法是计算线性变换作用于给定向量的一种途径,如图4所示。
这里重要的一点是,每当你看到一个矩阵时,你都可以把它解读为对空间的一种特定变换。
相关文章:

03 矩阵与线性变换
矩阵与线性变换 线性变换如何用数值描述线性变换特殊的线性变换反过来看总结 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 线性变换 如果一个变换具有以下两个性质,我们就称它是线性的: 一是直线在变换后仍然保持为直线二是原点必须…...
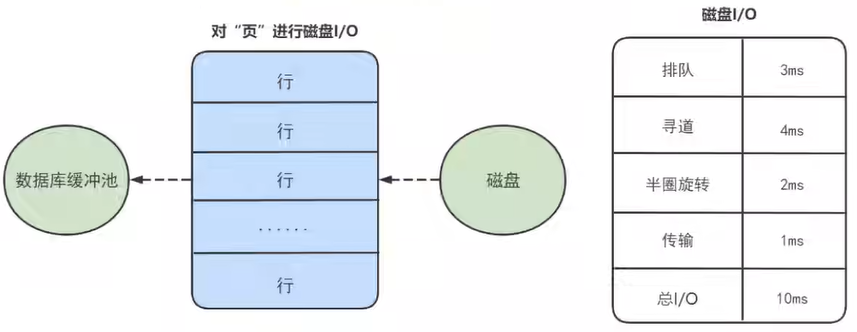
MySQL InnoDB数据存储结构
1. 数据库的存储结构:页 索引结构给我们提供了高效的索引方式,不过索引信息以及数据记录都是保存在文件上的,确切说是存储在页结构中。另一方面,索引是在存储引擎中实现的,MySQL服务器上的存储引擎负责对表中数据的读…...

【数据结构】数组和字符串(十五):字符串匹配2:KMP算法(Knuth-Morris-Pratt)
文章目录 4.3 字符串4.3.1 字符串的定义与存储4.3.2 字符串的基本操作4.3.3 模式匹配算法0. 朴素模式匹配算法1. ADL语言2. KMP算法分析3. 手动求失败函数定义例1例2例3 4. 自动求失败函数(C语言)5. KMP算法(C语言)6. 失败函数答案…...

STM32 PWM可控制电压原理
PWM可控制电压原理 主要通过PWM 输入模式根据控制单位时间内输出的平均电压,以调节电压大小。而PWM输出模式通过调节占空比,控制平均电压大小; 设置TIM为PWM输出模式 第一步:时钟使能: GPIO,TIM; 第二步&a…...

angular、 react、vue框架对比
借鉴:Web前端开发:三大主流框架 (baidu.com) AngularReactVue公司ChromeFaceBook尤雨溪写法有指令、模板的概念比较灵活,没有要求使用特定的架构和模式有指令和模板的概念性能低有虚拟Dom,性能高有虚拟Dome,性能高学习门槛 高&am…...

GNSS常用数据源汇总
本文整理汇总了GNSS数据处理过程中常用的数据源,路径中的占位符具体含义如下: -YYYY-年-YY-年的后两位数-DOY-年积日-MM-月-HH-小时-WWWW-GPS周 一、RINEXO观测值与RINEXN星历小时文件 1、CDDIS:ftp://gdc.cddis.eosdis.nasa.gov/pub/gnss…...
01|LangChain | 从入门到实战-介绍
by:wenwenc9 一、基本知识储备 1、什么是大模型,LLM? 大模型(Large Language Model)是近年来一个很热门的研究方向。 使用大量的数据训练出一个非常大的模型。一般是数十亿到上万亿的参数规模。 这些大模型可以捕捉到非常复杂的语言…...
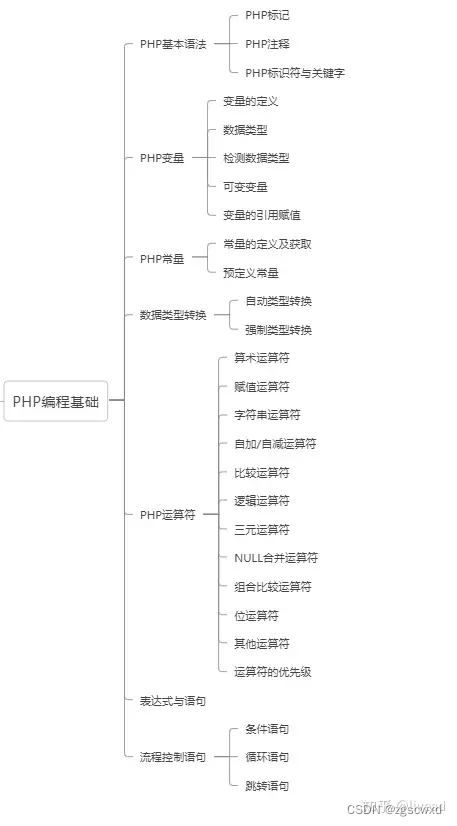
【小白专用】PHP基本语法 23.11.04
PHP基本语法 PHP是超文本预处理器 由服务器解析执行 可以与 html 进行混编(嵌入) ,PHP是一种弱类型语言 1.1 PHP标记 PHP和其他Web语言一样,都是用一对标记将PHP代码包含起来,以便和HTML代码区分开来。PHP支持4种风格的标记,如表所示。 标…...
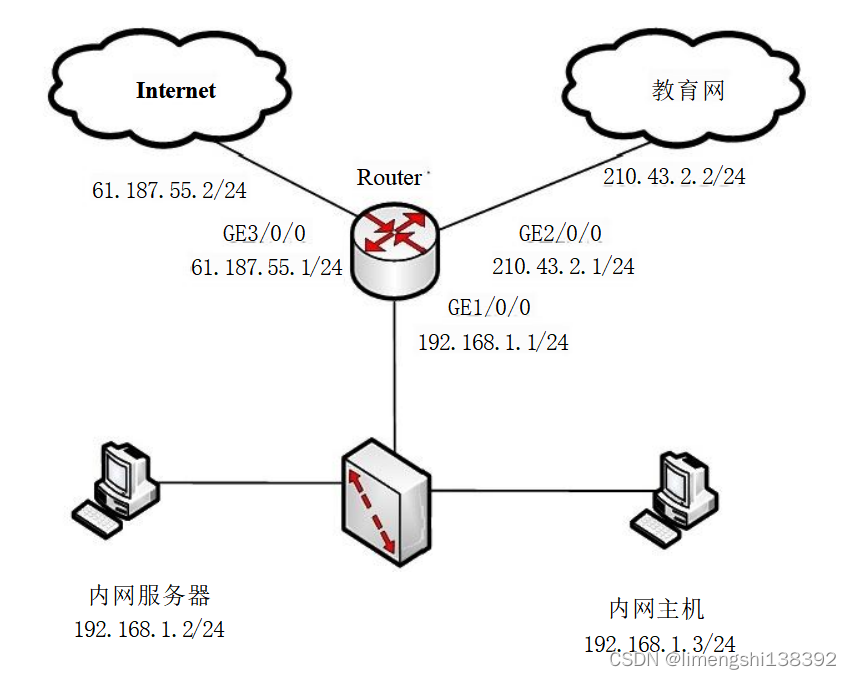
路由器基础(七):NAT原理与配置
一、NAT 配置 华为路由器配置NAT 的方式有很多种,考试中可能考到的基本配置方 式主要有EasyIP和通过NAT地址池的方式。图22-7-1是一个典型的通过EasyIP进行NAT的示意图,其中Router出接口GE0/0/1的IP地址为200.100.1.2/24,接口E0/0/1的IP地址为192.168.0.…...

Spring Boot 整合SpringSecurity和JWT和Redis实现统一鉴权认证
📑前言 本文主要讲了Spring Security文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是青衿🥇 ☁️博客首页:CSDN主页放风讲故事 🌄每日一句:努力…...
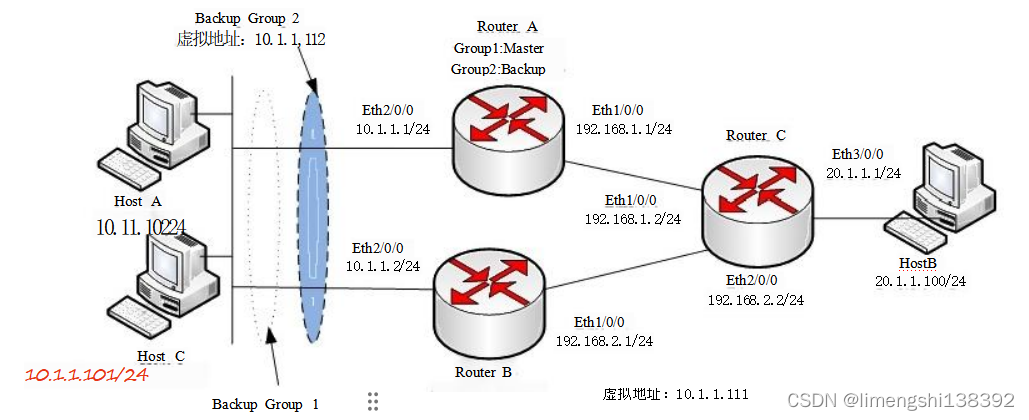
交换机基础(零):交换机基础配置
一、华为设备视图 常用视图 名称 进入视图 视图功能 用户视图 用户从终端成功登录至设备即进 入用户视图,在屏幕上显示 kHuawei> 用户可以完成查看运行状态和统 计信息等功能。在其他视图下 都可使用return直接返回用户视 图 系统视图 在用户视图下&…...

02 线性组合、张成的空间与基
线性组合、张成的空间与基 基向量缩放向量并相加给定向量张成的空间线性相关与线性无关空间的基 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 基向量 当看到一对描述向量的数时,比如[3,-2]时,把这对数中的每个数(坐标&…...
解析mfc100u.dll文件丢失的修复方法,快速解决mfc100u.dll问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中最常见的就是“缺少某个文件”的错误。最近,我也遇到了一个这样的问题,那就是“mfc100u.dll丢失”。这个问题可能会导致某些应用程序无法正常运行,给我们带来困扰。…...
免费外文文献检索网站,你一定要知道
01. Sci-Hub 网址链接:https://tool.yovisun.com/scihub/ Sci-hub是一个可以无限搜索、查阅和下载大量优质论文的数据库。其优点在于可以免费下载论文文献。 使用方法: 在Sci—hub搜索栏中粘贴所需文献的网址或者DOI,然后点击右侧的open即可…...

大数据毕业设计选题推荐-收视点播数据分析-Hadoop-Spark-Hive
✨作者主页:IT研究室✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Python…...
传智杯-21算法赛初赛B组题目详细解法解析-AB题(C/C++、Python、Java)
🚀 欢迎来到 ACM 算法题库专栏 🚀 在ACM算法题库专栏,热情推崇算法之美,精心整理了各类比赛题目的详细解法,包括但不限于ICPC、CCPC、蓝桥杯、LeetCode周赛、传智杯等等。无论您是刚刚踏入算法领域,还是经验丰富的竞赛选手,这里都是提升技能和知识的理想之地。 ✨ 经典…...

post给后端传递数组和多个参数
这是前端的数据结构 data() {return {loading: false,inputForm: {id: ${gridProject.id},gridName: ,gridId: ,projectName: ,projectId: ,type: },data: [],value: []}}, 其中 gridId 和 type 是单个参数 , value 是个数组,注意 这里data中的value[]不要直接给后…...
音频修复增强软件iZotope RX 10 mac中文特点
iZotope RX 10 mac是一款音频修复和增强软件。 iZotope RX 10 mac主要特点 声音修复:iZotope RX 10可以去除不良噪音、杂音、吱吱声等,使音频变得更加清晰干净。 音频增强:iZotope RX 10支持对音频进行音量调节、均衡器、压缩器、限制器等处…...

【面试】虚拟机栈面试题
目录 一、举例栈溢出的情况二、调整栈大小,能保证不出现溢出吗?三、分配的栈内存越大越好吗?四、垃圾回收是否会涉及到虚拟机栈?五、方法中定义的局部变量是否存在线程安全问题?5.1 说明5.2 代码示例 一、举例栈溢出的…...

白话熵增定律
白话熵增定律 热力学中的熵增定律 熵是指一个系统的混乱程度的度量,是热力学中的一个系统的属性。熵增定律是指一个封闭的系统随着时间的发展,在朝平衡状态发展时,其熵会增加,即其越来越混乱。 对于一个房间,如果经常…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
