LeetCode题解 动态规划(四):416 分割等和子集;1049 最后一块石头的重量 II
背包问题
下图将背包问题做了分类
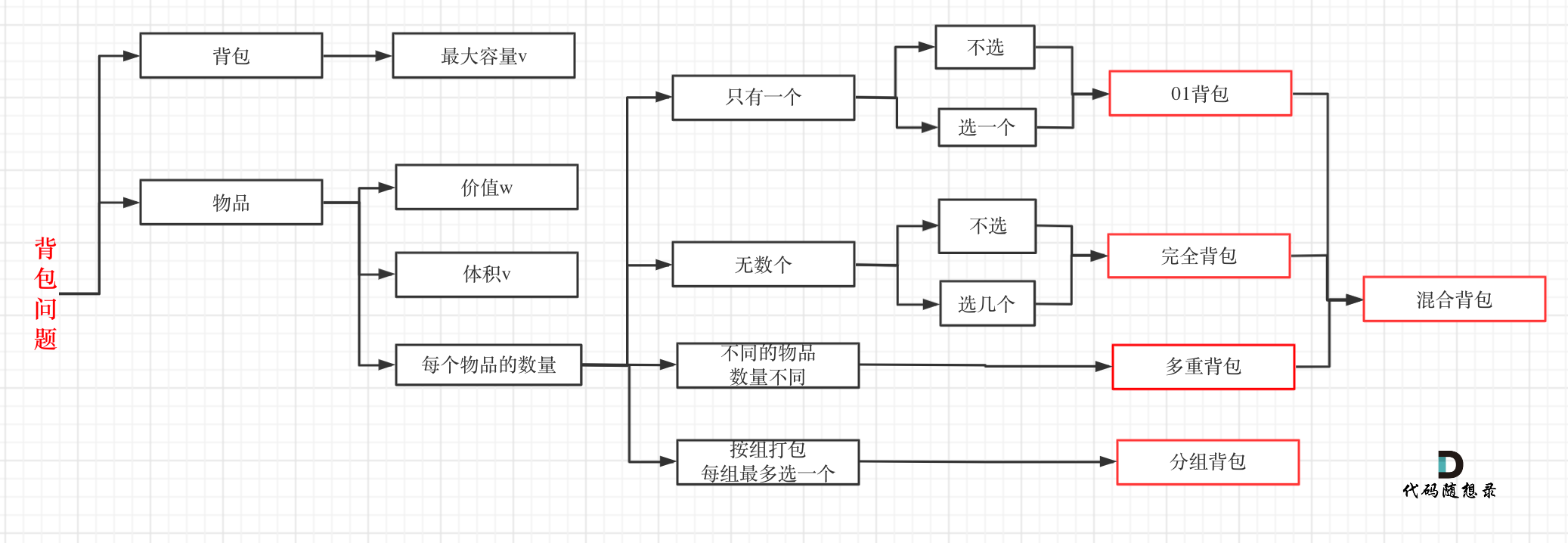
其中之重点,是01背包,即一堆物件选哪样不选哪样放入背包里。难度在于,以前的状态转移,多只用考虑一个变量,比如爬楼梯的阶层,路径点的选择,这也是能用滚动数组表示动态规划的原因,而现在要同时考虑两个:物品和背包容量。
01背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
使用动态规划五部曲:
1 - 确定dp数组含义:有一种写法, 是使用二维数组,即dp[i] [j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2 - 到了第 i 件物品的时候,背包容量为 j ,但就放不放物品,两种选择:
- 不放第 i 件物品,那么背包容量不变,从dp[i - 1] [j]状态而来
- 放第 i 件物品,那么就会从dp[i - 1] [j - weight[i]]状态而来,因为至少得有足够的空间将物品放进去才行。
所以递归公式: dp[i] [j] = max(dp[i - 1] [j], dp[i - 1] [j - weight[i]] + value[i]);
3 - 初始化dp数组:如果是01背包的话,背包容量如果为零,那么价值也一定为零。而能放入第一件物品的时候,就是其对应的价值。
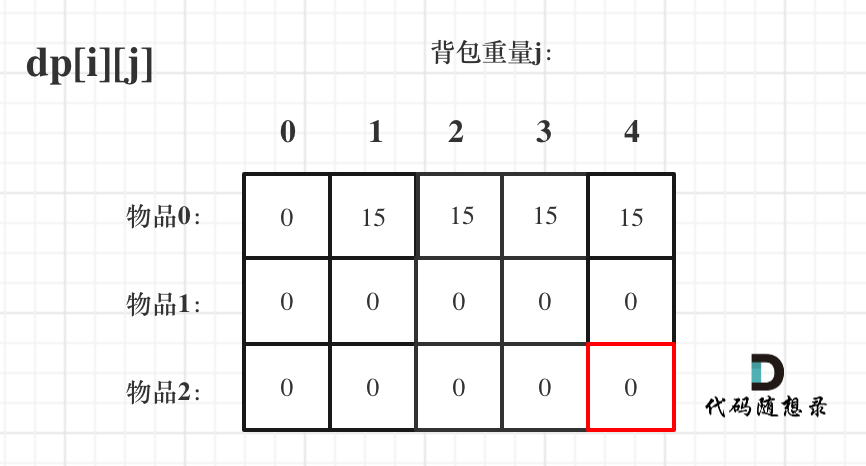
4 - 遍历顺序:这一步比较重要,在初期理解01背包的时候会显得有一点难以理解。但总归记住,就是一个二维数组,和之前的题目一样,先遍历物品再遍历背包容量(物品固定,尝试一点点把物品塞进去),和先遍历背包容量再遍历物品(背包容量固定,尝试能塞进去哪个)都是可以的。
从数组的角度考虑这一点也是可以的,根据递推公式,当前状态是从数组的左上角位置而来,只要保持是这个方向就可以了。就和我们之前求解路径问题时一样。
5 - 举例推导
假设背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
那么数组的最终状态就如下图所示:

关于01背包,也有使用一维数组,即滚动数组的方法。其核心思想是,如果不放物品,dp[j]其实就是自己本身,如果要放物品,那么dp[j] 就是考虑从一个能放下这个物品的背包,塞入该物品,即dp[j - weight[i]] + value[i]。
遍历顺序就是不能是从一个空背包开始放了,而是从一个满的背包里尝试取出某件物品,这样做是为了保证物品只被放入一次。这么做也是有现实依据的,就是先考虑所有能用得上的东西,再从这些物品里挑出来不是那么重要的物品。
我私认为,注重理论推导,就可以在后期的解题过程中方便不少,但是也不必过于纠结能否“记住理论”,还是要投入实际应用才能更好的理解理论。
接下来,进入解题过程。
416 分割等和子集 medium
给你一个 只包含正整数 的 非空 数组
nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
为什么说动态规划难呢?我认为是不少时候压根意识不到该用动态规划求解问题。
关于这道题,首先要想到要对整个数组求和,如果和是奇数,咋分都分不出来。
如果是偶数,那么所有数之和的一半,就是我们期望的“背包最大容量”,剩下的事情就是把数字填进去就可以了,和01背包完全一样。
根据这个思想,代码如下:
bool canPartition(vector<int>& nums) {int sum = 0;for (int num: nums)sum += num;if (sum % 2 == 1) return false;int target = sum / 2;vector<int> dp(10001, 0); // 题目中给出数组长度最大是200,值最大是100,取总和的一半肯定够了// 我们采用先遍历数字的方式for (int i = 0; i < nums.size(); ++i) {for (int j = target; j >= nums[i]; --j) {dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[target] == target;
}
1049 最后一块石头的重量 II medium
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
实不相瞒,以我现在的水平,看到这道题,我还是想不到应该用动态规划来做,但是多少有点儿那个味儿了。
要使最后剩下的石块重量尽可能小,就需要能撞掉的石头尽可能多,所以这道题可以看成是背包容量为[总重量/2](向下取整),物品价值就是石头重量的0-1背包问题。
求解方式和上面的题几乎一模一样,代码如下:
int lastStoneWeightII(vector<int>& stones) {int totalWeight = 0;for (int stoneWeight: stones)totalWeight += stoneWeight;vector<int> dp(15001, 0);int target = totalWeight / 2;for (int i = 0; i < stones.size(); ++i) {for (int stonesWeight = target; stonesWeight >= stones[i]; --stonesWeight) {dp[stonesWeight] = max(dp[stonesWeight], dp[stonesWeight - stones[i]] + stones[i]);}}return totalWeight - 2 * dp[target];
}
说到这里,可能还是有人不太明白为什么能这么写,之所以要尽量的往总数量一半的背包里塞,就说明这些都是希望能尽量被撞掉的,可以证明,如果能达到一半的容量,那么其必然可以全部被撞掉,所以最后要减去2倍的dp[target]。
相关文章:

LeetCode题解 动态规划(四):416 分割等和子集;1049 最后一块石头的重量 II
背包问题 下图将背包问题做了分类 其中之重点,是01背包,即一堆物件选哪样不选哪样放入背包里。难度在于,以前的状态转移,多只用考虑一个变量,比如爬楼梯的阶层,路径点的选择,这也是能用滚动数组…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(二)
demux模块 从前面一篇文章中可以得知,demux模块的使用方法大致如下: 分配AVFormatContext通过avformat_open_input(…)传入AVFormatContext指针和文件路径,启动demux通过av_read_frame(…) 从AVFormatContext中读取demux后的audio/video/subtitle数据包…...
PCIE 学习笔记(入门简介)
PCIE 学习笔记书到用时方恨少啊,一年前学PCIE的笔记,再拿出来瞅瞅。发到博客上,方便看。PCIE基础PCIE和PCI的不同PCIE采用差分信号传输,并且是dual-simplex传输——每条lane上有TX通道和RX通道,所以每条lane上的信号是…...
锁的优化机制了解嘛?请进!
点个关注,必回关 文章目录自旋锁:自适应锁:锁消除:锁粗化:偏向锁:轻量级锁:从JDK1.6版本之后,synchronized本身也在不断优化锁的机制,有些情况下他并不会是一个很重量级的…...

5.点赞功能 Redis
Redis(1)简介Redis 是一个高性能的 key-value 数据库原子 – Redis的所有操作都是原子性的。多个操作也支持事务,即原子性,通过MULTI和EXEC指令包起来。非关系形数据库数据全部存在内存中,性能高。(2&#…...
)
Java序列化和反序列化(详解)
一、理解Java序列化和反序列化 Serialization(序列化):将java对象以一连串的字节保存在磁盘文件中的过程,也可以说是保存java对象状态的过程。序列化可以将数据永久保存在磁盘上(通常保存在文件中)。 deserialization(反序列化):将保存在磁…...

【刷题篇】链表(上)
前言🌈前段时间我们学习了单向链表和双向链表,本期将带来3道与链表相关的OJ题来巩固对链表的理解。话不多说,让我们进入今天的题目吧!🚀本期的题目有:反转单链表、链表的中间结点、合并两个有序链表反转单链…...

ConcurrentHashMap设计思路
ConcurrentHashMap设计思路Hashtable vs ConcurrentHashMapHashtable vs ConcurrentHashMap Hashtable 对比 ConcurrentHashMap Hashtable 与 ConcurrentHashMap 都是线程安全的 Map 集合Hashtable 并发度低,整个 Hashtable 对应一把锁,同一时刻&#…...

Unity基于GraphView的行为树编辑器
这里写自定义目录标题概述基于GitHub上:目前这只是做了一些比较基础的功能节点开发,仅仅用于学习交流,非完成品。项目GitHub连接:[https://github.com/HengyuanLee/BehaviorTreeExamples](https://github.com/HengyuanLee/Behavio…...
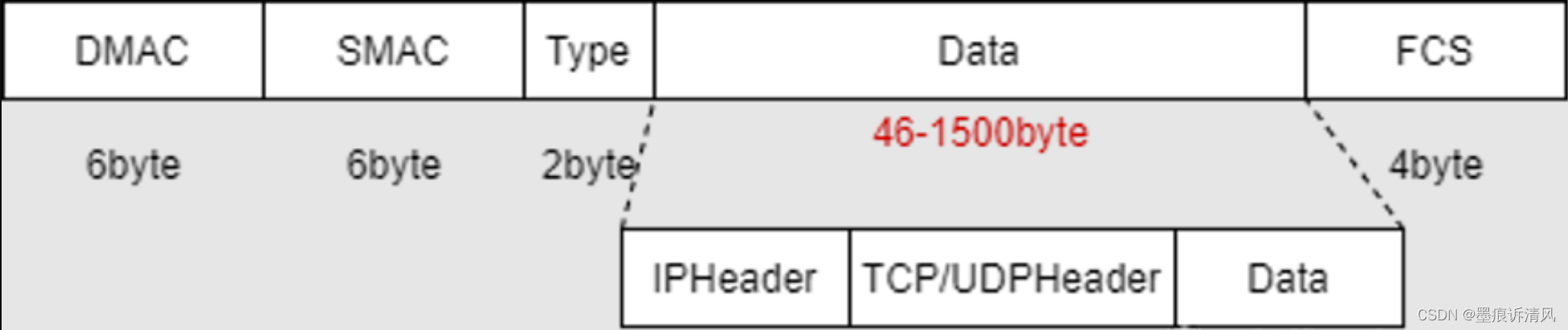
网络流量传输MTU解析
基本概念 以太网的链路层对数据帧的长度会有一个限制,其最大值默认是1500字节,链路层的这个特性称为MTU,即最大传输单元 Maximum Transmission Unit,最大传输单元,指的是数据链路层的最大payload,由硬件网…...
)
30个HTML+CSS前端开发案例(四)
30个HTMLCSS前端开发案例(17-20)鼠标移入文字加载动画效果代码实现效果鼠标悬停缩放效果实现代码效果鼠标移入旋转动画实现代码效果loding加载动画实现代码效果资源包鼠标移入文字加载动画效果 代码实现 <!DOCTYPE html> <html><head&g…...

《TPM原理及应用指南》学习 —— TPM执行环境3
本文对应《A Practical Guide to TPM 2.0 — Using the Trusted Platform Module in the New Age of Security》的第6章第3节。 6.3 Summary —— 总结 Now that you have an execution environment (or maybe both of them) set up, you’re ready to run the code samples f…...
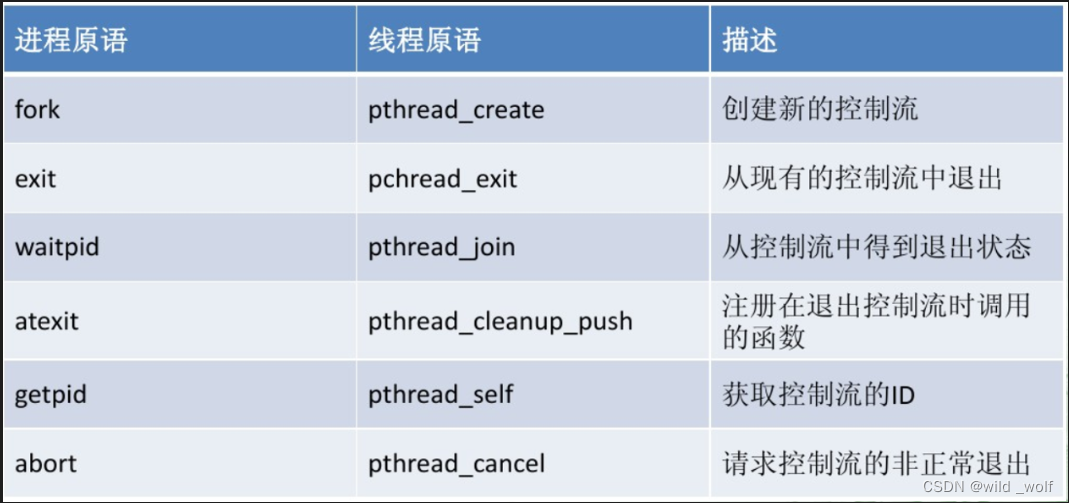
实验名称:经典同步问题:生成者与消费者问题
实验名称:经典同步问题:生成者与消费者问题 相关知识 信号量 信号量是用来协调不同进程间的数据对象,可用来保护共享资源,也能用来实现进程间及同一进程不同线程间的进程同步。分为二值信号灯和计算信号灯两种类型。 进程与线…...

EasyCVR视频云存储的架构解析与Sharelist云存挂载方法介绍
一、什么是视频云存储? 视频云存储主要用于为上层应用提供视频文件、结构化信息、事件信息的相关服务。云存储节点分为数据文件存储节点和结构化数据存储节点。数据文件存储节点主要用于视频、图片的存储。结构化数据存储节点用于存储结构化数据并提供相关服务。 …...
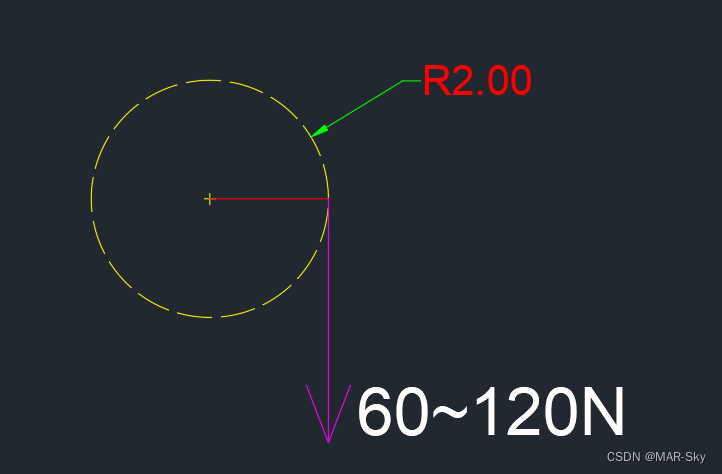
电机参数中力矩单位kgf.cm,Nm,mNm表示的含义
力的基本知识 质量和力的比例系数 质量和重力的关系有一个重力系数:g≈9.8 N/kg≈10,后面看到的1kgf就相当于1kg物体的力也就是10N 杠杆原理 对于同一个支点,在不考虑杠杆的重量的情况下,实现同样的作用效果,距离支点越近&…...

使用scikit-learn为PyTorch 模型进行超参数网格搜索
scikit-learn是Python中最好的机器学习库,而PyTorch又为我们构建模型提供了方便的操作,能否将它们的优点整合起来呢?在本文中,我们将介绍如何使用 scikit-learn中的网格搜索功能来调整 PyTorch 深度学习模型的超参数: 如何包装 P…...
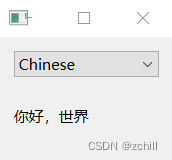
Windeployqt 打包,缺少dll 的解决方法
Windeployqt 打包,缺少DLL 的原因分析,解决方法 很多同学使用工具windeployqt进行打包发布后,运行exe文件时,还是会出现下图所示的系统错误提示,这种情况就表示相关的DLL 库文件没有被正确打包。可是windeployqt明确显…...
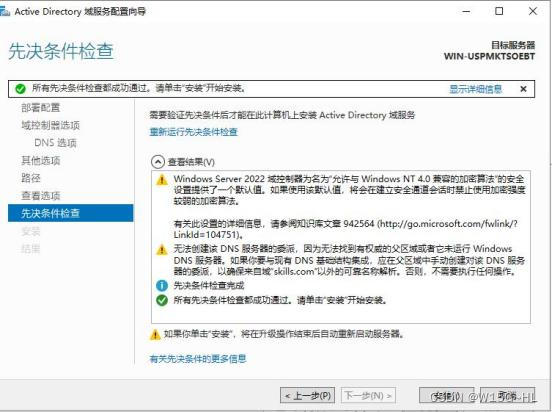
第四章:搭建Windows server AD域和树域
由于Windows简单一点,我就先搞Windows了。AD域:视频教程:https://www.bilibili.com/video/BV1f84y1G72x/在创建AD域时要把网卡配置好这是打开网卡界面的命令DNS要改成自己的,因为在创建域的同时也会自动创建DNS打开服务器管理器&a…...

【解决方案】老旧小区升级改造,视频智能化能力如何提升居民安全感?
一、需求背景 随着我国社会经济的快速发展与进步,城市宜居程度成为城市发展的重要指标,城市的发展面临着更新、改造和宜居建设等。一方面,社区居民对生活的环境提出了更高的要求;另一方面,将“智慧城市”的概念引入社…...
【遇见青山】项目难点:缓存穿透的解决方案
【遇见青山】项目难点:缓存穿透的解决方案1.缓存穿透现象缓存空对象布隆过滤其他方案2.解决方案,缓存空数据1.缓存穿透现象 缓存穿透是指客户端请求的数据在缓存中和数据库中都不存在,这样缓存永远不会生效,这些请求都会打到数据…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
