机器学习---支持向量机的初步理解
1. SVM的经典解释
改编自支持向量机解释得很好 |字节大小生物学 (bytesizebio.net)
话说,在遥远的从前,有一只贪玩爱搞破坏的妖怪阿布劫持了善良美丽的女主小美,智勇双全
的男主大壮挺身而出,大壮跟随阿布来到了妖怪的住处,于是,妖怪将两种能量球吐到了桌子上,
并要求大壮用他手里的棍子将两种能量球分开,如果大壮能赢得游戏,就成全他和小美。

大壮思索了片刻,就将他手里的棍子放了上去,正好将两种能量球分到不同阵营。

然后阿布胸有成竹的又吐出了新的球,恰巧有一个球在不属于他的阵营。

大壮将手里的棍子变粗,并试图通过在棍子两侧留出尽可能大的间隙来将棍子放在最佳位置。

阿布气急败坏,将桌子上的能量球全部打乱顺序。

大壮一时间想不出办法,阿布转身就要和小美去玩游戏,大壮很生气的拍了一下桌子,恍然
大悟,并将手里的棍子扔了出去。

在阿布的眼中,棍子正好穿过了所有的能量球,并将其划分在不同的领域。

棍子也恰好打在了阿布的头上,大壮和小美幸福的生活在了一起。
经过后人的杜篡,将球写成了数据(data),将棍子写为了分类(classifier ),将最大间隙
写成了最优化(optimization)、将拍桌子描绘成核方法(kernelling),将桌子写为超平面
(hyperplane)。
2. SVM的算法定义
SVM全称是supported vector machine(⽀持向量机),即寻找到⼀个超平⾯使样本分成两
类,并且间隔最大。 SVM能够执⾏线性或非线性分类、回归,甚⾄是异常值检测任务。它是机器
学习领域最受欢迎的模型之⼀。SVM特别适用于中小型复杂数据集的分类。

超平面最⼤间隔介绍:
上左图显示了三种可能的线性分类器的决策边界:虚线所代表的模型表现非常糟糕,甚至都
⽆法正确实现分类。其余两个模型在这个训练集上表现堪称完美,但是它们的决策边界与实例过于
接近,导致在面对新实例时,表现可能不会太好。 右图中的实线代表SVM分类器的决策边界,不
仅分离了两个类别,且尽可能远离最近的训练实例。
2.1 硬间隔
在上面我们使用超平⾯进行分割数据的过程中,如果我们严格地让所有实例都不在最⼤间隔之
间,并且位于正确的⼀边,这就是硬间隔分类。 硬间隔分类有两个问题,⾸先,它只在数据是线
性可分离的时候才有效;其次,它对异常值非常敏感。
当有⼀个额外异常值的鸢尾花数据:左图的数据根本找不出硬间隔,⽽右图最终显示的决策
边界与我们之前所看到的⽆异常值时的决策边界也⼤不相同,可能⽆法很好地泛化。

2.2 软间隔
要避免这些问题,最好使⽤更灵活的模型。⽬标是尽可能在保持最⼤间隔宽阔和限制间隔违
例(即位于最⼤间隔之上, 甚⾄在错误的⼀边的实例)之间找到良好的平衡,这就是软间隔分
类。 要避免这些问题,最好使⽤更灵活的模型。⽬标是尽可能在保持间隔宽阔和限制间隔违例之
间找到良好的平衡,这就是软间隔分类。

在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:C值越小,则间隔越宽,但是
间隔违例也会越多。上图显示了在⼀个非线性可分离数据集上,两个软间隔SVM分类器各自的决
策边界和间隔。 左边使用了高C值,分类器的错误样本(间隔违例)较少,但是间隔也较小。 右
边使用了低C值,间隔大了很多,但是位于间隔上的实例也更多。看起来第⼆个分类器的泛化效果
更好,因为⼤多数间隔违例实际上都位于决策边界正确的⼀边,所以即便是在该训练集上,它做出
的错误预测也会更少。
3. SVM的损失函数
在SVM中,我们主要讨论三种损失函数:

绿色:0/1损失
当正例的点落在y=0这个超平⾯的下边,说明是分类正确,⽆论距离超平⾯所远多近,误差都是0。
当这个正例的样本点落在y=0的上方,说明分类错误,⽆论距离多远多近,误差都为1。
图像就是上图绿色线。
蓝色:SVM Hinge损失函数
当⼀个正例点落在y=1的直线上,距离超平面长度1,那么1-ξ=1,ξ=0,也就是说误差为0。
当它落在距离超平面0.5的地方,1-ξ=0.5,ξ=0.5,也就是说误差为0.5。
当它落在y=0上的时候,距离为0,1-ξ=0,ξ=1,误差为1。
当这个点落在了y=0的上方,被误分到了负例中,距离算出来应该是负的,比如-0.5,那么1-
ξ=-0.5,ξ=1.5。误差为1.5。
以此类推,画在⼆维坐标上就是上图中蓝色那根线了。
红色:Logistic损失函数
损失函数的公式为:![]()
当y = 0时,损失等于ln2,这样线很难画,所以给这个损失函数除以ln2,这样到y = 0时,损
失为1,即损失函数过(0,1)点,即上图中的红色线。
4. SVM的核方法
核函数并不是SVM特有的,核函数可以和其他算法也进⾏结合,只是核函数与SVM结合的优
势非常⼤。核函数,是将原始输⼊空间映射到新的特征空间,从而,使得原本线性不可分的样本可
能在核空间可分。

下图所示的两类数据,分别分布为两个圆圈的形状,这样的数据本身就是线性不可分的,此时
该如何把这两类数据分开呢?

假设X是输⼊空间, H是特征空间, 存在⼀个映射ϕ使得X中的点x能够计算得到H空间中的点
h, 对于所有的X中的点都成立:
![]()
若x,z是X空间中的点,函数k(x,z)满足下述条件,则称k为核函数,⽽ϕ为映射函数:

核方法案例1:



 经过上⾯公式,具体变换过过程为:
经过上⾯公式,具体变换过过程为:

核方法案例2:
下⾯这张图位于第⼀、⼆象限内。我们关注红色的门,以及“北京四合院”这⼏个字和下面的紫
色的字母。 下⾯这张图位于第⼀、⼆象限内。我们关注红色的门,以及“北京四合院”这几个字和下
⾯的紫色的字母。


绿色的平面可以完美地分割红色和紫色,两类数据在三维空间中变成线性可分的了。 三维中
的这个判决边界,再映射回⼆维空间中:是⼀条双曲线,它不是线性的。 核函数的作用就是⼀个
从低维空间到高维空间的映射,⽽这个映射可以把低维空间中线性不可分的两类点变成线性可分
的。

常见的核函数:
 1.多项核中,d=1时,退化为线性核;
1.多项核中,d=1时,退化为线性核;
2.高斯核亦称为RBF核。
线性核和多项式核:
这两种核的作用也是⾸先在属性空间中找到⼀些点,把这些点当做base,核函数的作用就是
找与该点距离和角度满足某种关系的样本点。
当样本点与该点的夹角近乎垂直时,两个样本的欧式长度必须非常长才能保证满足线性核函
数大于0;而当样本点与base点的方向相同时,长度就不必很长;而当方向相反时,核函数值就是
负的,被判为反类。即它在空间上划分出⼀个梭形,按照梭形来进⾏正反类划分。
RBF核:
高斯核函数就是在属性空间中找到⼀些点,这些点可以是也可以不是样本点,把这些点当做
base,以这些 base 为圆心向外扩展,扩展半径即为带宽,即可划分数据。 换句话说,在属性空
间中找到⼀些超圆,⽤这些超圆来判定正反类。
Sigmoid核:
同样地是定义⼀些base, 核函数就是将线性核函数经过⼀个tanh函数进⾏处理,把值域限制
在了-1到1上。 总之,都是在定义距离,⼤于该距离,判为正,小于该距离,判为负。至于选择哪
⼀种核函数,要根据具体的样本分布情况来确定。
⼀般有如下指导规则:
1) 如果Feature的数量很大,甚至和样本数量差不多时,往往线性可分,这时选用LR或者线
性核Linear;
2) 如果Feature的数量很小,样本数量正常,不算多也不算少,这时选用RBF核;
3) 如果Feature的数量很小,而样本的数量很大,这时⼿动添加⼀些Feature,使得线性可
分,然后选用LR或者线性核Linear;
4) 多项式核⼀般很少使用,效率不高,结果也不优于RBF;
5) Linear核参数少,速度快;RBF核参数多,分类结果⾮常依赖于参数,需要交叉验证或网
格搜索最佳参数,⽐较耗时;
6)应用最⼴的应该就是RBF核,⽆论是小样本还是⼤样本,高维还是低维等情况,RBF核函
数均适用。
相关文章:

机器学习---支持向量机的初步理解
1. SVM的经典解释 改编自支持向量机解释得很好 |字节大小生物学 (bytesizebio.net) 话说,在遥远的从前,有一只贪玩爱搞破坏的妖怪阿布劫持了善良美丽的女主小美,智勇双全 的男主大壮挺身而出,大壮跟随阿布来到了妖怪的住处&…...

【unity实战】Unity实现2D人物双击疾跑
最终效果 前言 我们要实现的功能是双击疾跑,当玩家快速地按下同一个移动键两次时能进入跑步状态 我假设快速按下的定义为0.2秒内,按下同一按键两次 简单的分析一下需求,实现它的关键在于获得按键按下的时间,我们需要知道第一次…...

Spring面试题:(二)基于xml方式的Spring配置
xml配置Bean的常见属性 id属性 name属性 scope属性 lazy-init属性 init-method属性和destroy属性 initializingBean方法 Bean实例化方式 ApplicationContext底层调用BeanFactory创建Bean,BeanFactory可以利用反射机制调用构造方法实例化Bean,也可采用工…...
XR Interaction ToolKit
一、简介 XR Interaction Toolkit是unity官方的XR交互工具包。 官方XRI示例地址:https://github.com/Unity-Technologies/XR-Interaction-Toolkit-Examples 2023.3.14官方博客,XRIT v2.3 https://blog.unity.com/engine-platform/whats-new-in-xr-int…...

spring-boot中实现分片上传文件
一、上传文件基本实现 1、前端效果图展示,这里使用element-ui plus来展示样式效果 2、基础代码如下 <template><div><el-uploadref"uploadRef"class"upload-demo":limit"1":on-change"handleExceed":auto-…...
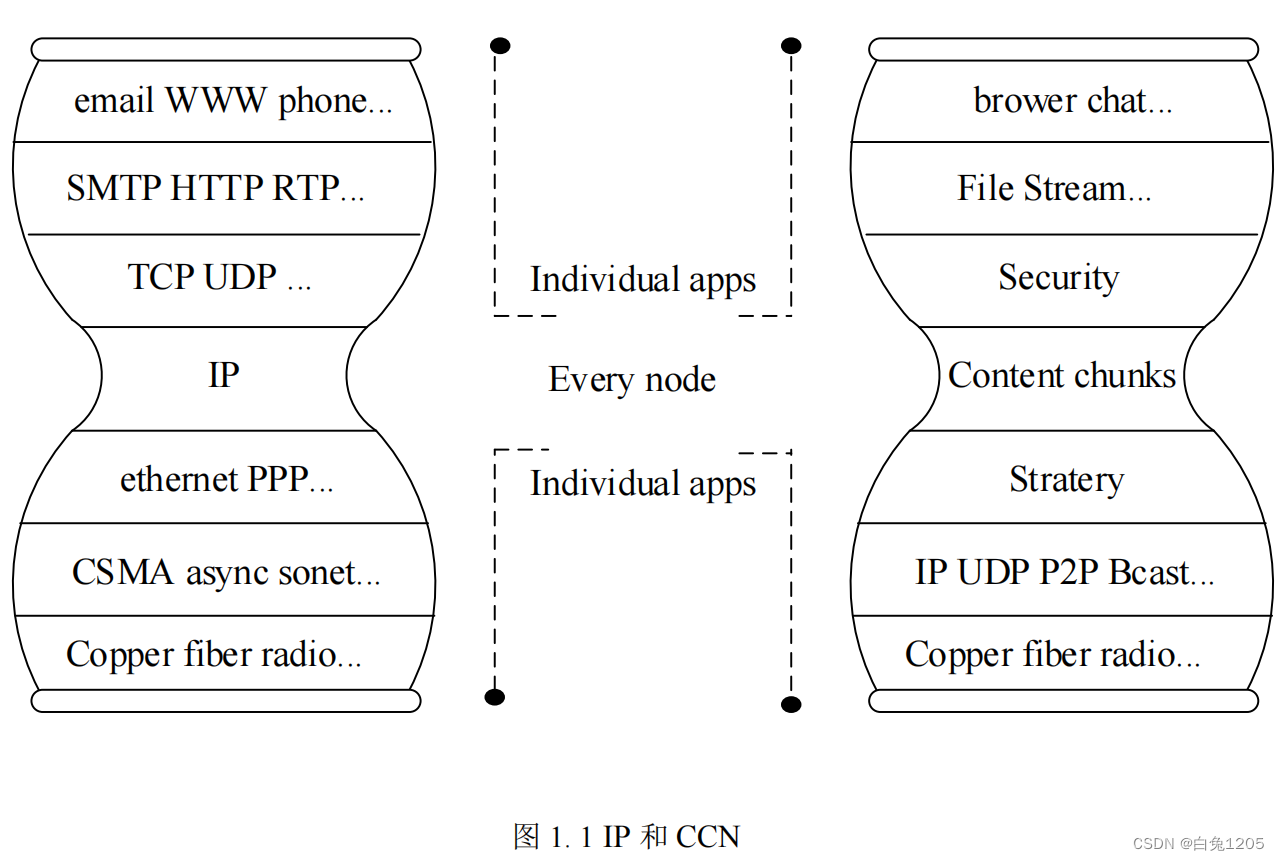
【ICN综述】信息中心网络隐私安全
ICN基本原理: 信息中心网络也是需要实现在不可信环境下可靠的信息交换和身份认证 信息中心网络采用以数据内容为中心的传输方式代替现有IP 网络中以主机为中心的通信方式,淡化信息数据物理或逻辑位置的重要性,以内容标识为代表实现数据的查找…...

基于STC12C5A60S2系列1T 8051单片机EEPROM应用
基于STC12C5A60S2系列1T 8051单片机EEPROM应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍STC12C5A60S2系列1T 8051单片机EEPROM介绍基于STC12C5A60S2系列1T 8051单…...

手撕排序之直接选择排序
前言: 直接选择排序是排序中比较简单的排序,同时也是时间复杂度不是很优的排序。 思想: 本文主要讲解直接选择排序的优化版本。 我们经过一次遍历直接将该数列中最大的和最小的值挑选出来,如果是升序,就将最小的和…...

洛谷 P1359 租用游艇
题目链接 P1359 租用游艇 普及 题目描述 长江游艇俱乐部在长江上设置了 n n n 个游艇出租站 1 , 2 , 3 , . . . , n 1,2,3,...,n 1,2,3,...,n,游客可在这些游艇出租站租用游艇,并在下游的任何一个游艇出租站归还游艇。游艇出租站 i i i 到游艇出租站…...

springboot中没有主清单属性解决办法
在执行一个 spring boot 启动类时,提示 没有主清单属性 一般这个问题是没加 spring-boot-maven-plugin 插件的问题,但是项目中已经加了 <build><plugins><plugin><groupId>org.springframework.boot</groupId><artifa…...

C/C++ static关键字详解(最全解析,static是什么,static如何使用,static的常考面试题)
目录 一、前言 二、static关键字是什么? 三、static关键字修饰的对象是什么? 四、C 语言中的 static 🍎static的C用法 🍉static的重点概念 🍐static修饰局部变量 💦static在修饰局部变量和函数的作用 &a…...
windwos10搭建我的世界服务器,并通过内网穿透实现联机游戏Minecraft
文章目录 1. Java环境搭建2.安装我的世界Minecraft服务3. 启动我的世界服务4.局域网测试连接我的世界服务器5. 安装cpolar内网穿透6. 创建隧道映射内网端口7. 测试公网远程联机8. 配置固定TCP端口地址8.1 保留一个固定tcp地址8.2 配置固定tcp地址 9. 使用固定公网地址远程联机 …...
【实战Flask API项目指南】之七 用JWT进行用户认证与授权
实战Flask API项目指南之 用JWT进行用户认证与授权 本系列文章将带你深入探索实战Flask API项目指南,通过跟随小菜的学习之旅,你将逐步掌握 Flask 在实际项目中的应用。让我们一起踏上这个精彩的学习之旅吧! 前言 当小菜踏入Flask后端开发…...
鸿蒙LiteOs读源码教程+向LiteOS中添加一个简单的基于线程运行时的短作业优先调度策略
【⭐据说点赞收藏的都会收获好运哦👍】 一、鸿蒙Liteos读源码教程 鸿蒙的源码是放在openharmony文件夹下,openharmony下的kernel文件夹存放操作系统内核的相关代码和实现。 内核是操作系统的核心部分,所以像负责:资源管理、任…...

axios的使用与封装详细教程
目录 一、axios使用方式二、axios在main.js配置 一、axios使用方式 在 Spring Boot Vue 的项目中使用 Axios,你需要在 Vue 项目中安装 Axios 库,因为 Axios 是一个前端 JavaScript 库,用于发送 HTTP 请求和处理响应数据,而与 Sp…...
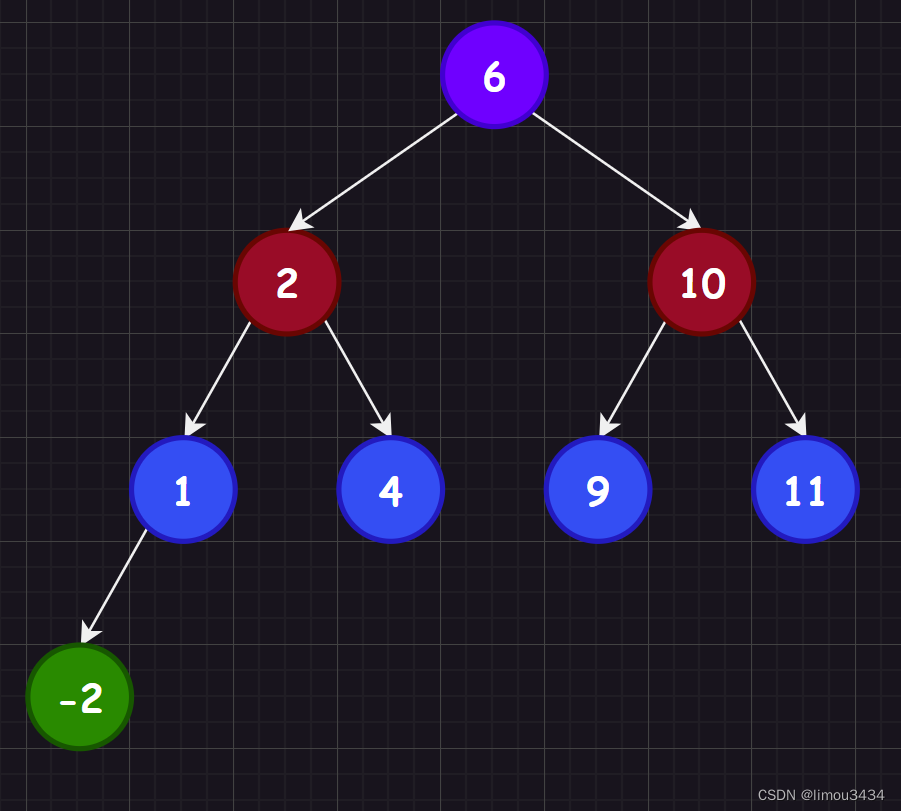
C++二叉搜索树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。 1.二叉搜索树概念 二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树…...
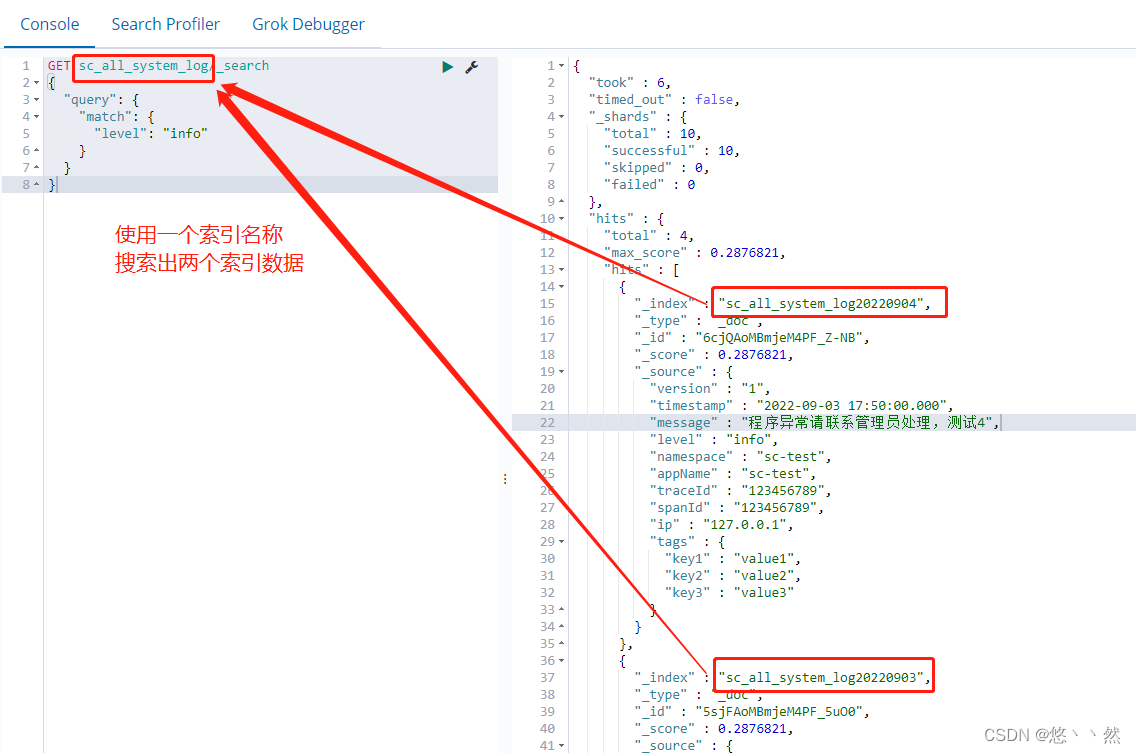
elasticsearch索引按日期拆分
1.索引拆分原因 如果单个索引数据量过大会导致搜索变慢,而且不方便清理历史数据。 例如日志数据每天量很大,而且需要定期清理以往日志数据。例如原索引为sc_all_system_log,现按天拆分索引sc_all_system_log20220902,sc_all_syste…...

纯python实现大漠图色功能
大漠图色是一种自动化测试工具,可以用于识别屏幕上的图像并执行相应的操作。在Python中,可以使用第三方库pyautogui来实现大漠图色功能。具体步骤如下: 安装pyautogui库:在命令行中输入pip install pyautogui。导入pyautogui库&a…...

debounce and throtlle
debounce // 核心:单位时间内触发>1 则只执行最后一次。//excutioner 可以认为是执行器。执行器存在则清空,再赋值新的执行器。function debounce(fn, delay 500) {let excutioner null;return function () {let context this;let args arguments…...

四、数据库系统
数据库系统(Database System),是由数据库及其管理软件组成的系统。数据库系统是为适应数据处理的需要而发展起来的一种较为理想的数据处理系统,也是一个为实际可运行的存储、维护和应用系统提供数据的软件系统,是存储介…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
