椭圆滤波器
之前的文章 信号去噪 中列出了7种常用的信号去噪算法,对于后两种算法——深度学习和奇异值分解(SVD),我现在也不太理解,就先不写了。
很多朋友留言又提了一些算法,今天一起来聊聊椭圆滤波器。
椭圆滤波器(Elliptic Filter),也称为Cauer滤波器,是一种数字滤波器,用于信号处理和滤波应用。椭圆滤波器之所以得名,是因为其在频率响应图上的特征呈现出椭圆形的形状。
椭圆滤波器有以下特点和优点:
-
极窄的过渡带宽:椭圆滤波器的过渡带宽(即通频带到阻频带的过渡区域)非常窄,这意味着它可以在频域内实现非常陡峭的滤波特性。
-
通带和阻带均衡:椭圆滤波器通常可以在通带和阻带内实现更好的幅度响应均衡。这意味着它可以在通带内最小化幅度失真,并在阻带内最大化信号抑制。
-
允许通带和阻带的波动:与其他滤波器设计相比,椭圆滤波器允许通带和阻带内的振荡,但在给定的通带和阻带容限下,可以实现更小的阶数(更低的复杂度)。
-
高阶滤波特性:椭圆滤波器通常以较高的阶数实现,这使其适用于需要极高滤波性能的应用,如无线通信和雷达系统。
椭圆滤波器的设计需要确定以下参数:
- 通带边界频率(通带上下限的频率)。
- 阻带边界频率(阻带上下限的频率)。
- 通带最大允许波纹(通带内振荡的幅度波纹)。
- 阻带最小抑制(阻带内信号抑制的最小要求)。
椭圆滤波器设计通常涉及到数学优化问题,以找到最佳参数配置来满足上述要求。
椭圆滤波器的设计
滤波器的目标
任何滤波器的目标都是根据特定的频率响应特性来修改输入信号的频谱。在椭圆滤波器中,通常有以下几个重要的频率响应特性目标:
- 通带(Passband):这是允许信号通过的频率范围,通常是我们希望保留的信号频率范围。
- 阻带(Stopband):这是我们希望完全抑制的频率范围,通常包括噪声或干扰信号。
- 过渡带(Transition Band):这是从通带到阻带之间的频率范围,通常需要在此范围内实现平滑的过渡。
频率响应特性
椭圆滤波器的主要特点是它在通带和阻带内具有波纹,这意味着幅度响应在这些频率范围内会波动。设计椭圆滤波器时,需要指定以下几个关键参数:
- 通带上限和下限频率。
- 阻带上限和下限频率。
- 通带内的最大允许波纹(通带内振荡的幅度波纹)。
- 阻带内的最小抑制要求(阻带内信号抑制的最小要求)。
设计优化
设计椭圆滤波器通常是一个优化问题,其中的目标是找到一组滤波器系数,以满足上述频率响应特性和参数要求。这个问题通常涉及到复杂的数学和优化算法。
阶数
椭圆滤波器的性能和复杂度与其阶数有关。阶数是滤波器的系数数量,通常以n表示。增加阶数可以提高滤波器的性能,但也会增加计算复杂度。
通带和阻带特性
椭圆滤波器的主要特点是通带和阻带内的波纹,这些波纹是通过合适的设计参数来控制的。通带波纹是通带内的最大振荡幅度,而阻带波纹是阻带内允许的最小信号抑制。
通带和阻带边界
设计椭圆滤波器时,需要指定通带和阻带的频率边界。这些边界决定了滤波器在哪些频率范围内工作以及哪些频率范围内抑制信号。
滤波器的实现
一旦设计出椭圆滤波器的系数,它可以被实现为数字滤波器。在数字信号处理中,可以使用差分方程或频域方法来应用这些系数。
性能权衡
椭圆滤波器的设计涉及性能和复杂度之间的权衡。增加阶数和降低通带和阻带波纹可以提高性能,但会增加计算复杂度。设计者需要根据具体应用的需求来选择合适的权衡。
应用
椭圆滤波器在各种领域都有广泛的应用,包括通信、图像处理、生物医学工程和音频处理等。下面是椭圆滤波器在音频处理中的应用实例之一——音频均衡器。
应用实例:音频均衡器
音频均衡器是音频处理中常见的设备,用于调整不同频率范围内的音频信号的增益,以满足特定的声音质量和音频效果要求。通常,音频均衡器分为多个频带,每个频带可以独立地调整增益,以实现音频的均衡。
在音频均衡器中,椭圆滤波器用于实现不同频带的均衡。每个频带都有一个椭圆滤波器,它可以调整该频带内的音频信号的增益,同时保持其他频带不受影响。以下是一个音频均衡器的应用示例:
信号描述: 假设我们有一个音频均衡器,它分为低音、中音和高音三个频带。我们希望用户能够通过调整这三个频带的增益来实现音频的均衡,即增强或减弱不同频率范围内的声音。
解决方案: 对于每个频带,我们可以使用椭圆滤波器来实现频率范围内的增益控制。椭圆滤波器的通带可以定位在相应频带内,而阻带则可以防止信号泄漏到其他频带。用户可以通过旋钮或界面上的控制来调整每个频带的增益。
性能: 椭圆滤波器可以设计为非常陡峭的滤波器,具有出色的频率选择和抑制特性。这使得它们非常适合用于音频均衡器,因为它们可以准确地控制每个频带的音频信号,而不会对其他频带产生不希望的影响。
实际应用: 音频均衡器广泛用于音响系统、录音室设备、电视和广播设备等领域。用户可以根据音频播放环境和个人喜好来调整音频的均衡,以获得更好的音质和听觉体验。
这个示例说明了椭圆滤波器在音频均衡器中的应用,帮助实现不同频带的音频均衡和定制。这对于音频处理和音响应用中的声音调整非常重要。
python示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import ellip, lfilter
from scipy.fft import fft# 生成一个示例音频信号
fs = 44100 # 采样率
t = np.arange(0, 0.1, 1/fs) # 时间向量
frequencies = [100, 500, 1000, 5000] # 音频信号的频率成分
signal = np.sum([np.sin(2 * np.pi * f * t) for f in frequencies], axis=0)# 设计椭圆滤波器
# 假设我们有3个频带,每个频带的通带和阻带频率范围由用户定义
band1 = (50, 200) # 低音频带
band2 = (400, 800) # 中音频带
band3 = (800, 5000) # 高音频带# 设计低音频带的椭圆滤波器
low_band = ellip(4, 0.05, 40, [2 * f / fs for f in band1], 'bandpass', analog=False)# 设计中音频带的椭圆滤波器
mid_band = ellip(4, 0.5, 40, [2 * f / fs for f in band2], 'bandpass', analog=False)# 设计高音频带的椭圆滤波器
high_band = ellip(4, 0.5, 40, [2 * f / fs for f in band3], 'bandpass', analog=False)# 使用滤波器处理信号
filtered_signal1 = lfilter(*low_band, signal)
filtered_signal2 = lfilter(*mid_band, signal)
filtered_signal3 = lfilter(*high_band, signal)# 计算频谱
def calculate_spectrum(x, fs):N = len(x)spectrum = np.abs(fft(x))[:N // 2]frequency = np.fft.fftfreq(N, 1 / fs)[:N // 2]return frequency, spectrum# 计算原始信号的频谱
freq_original, spec_original = calculate_spectrum(signal, fs)# 计算处理后的信号频谱
freq_filtered1, spec_filtered1 = calculate_spectrum(filtered_signal1, fs)
freq_filtered2, spec_filtered2 = calculate_spectrum(filtered_signal2, fs)
freq_filtered3, spec_filtered3 = calculate_spectrum(filtered_signal3, fs)# 绘制原始信号和处理后的信号
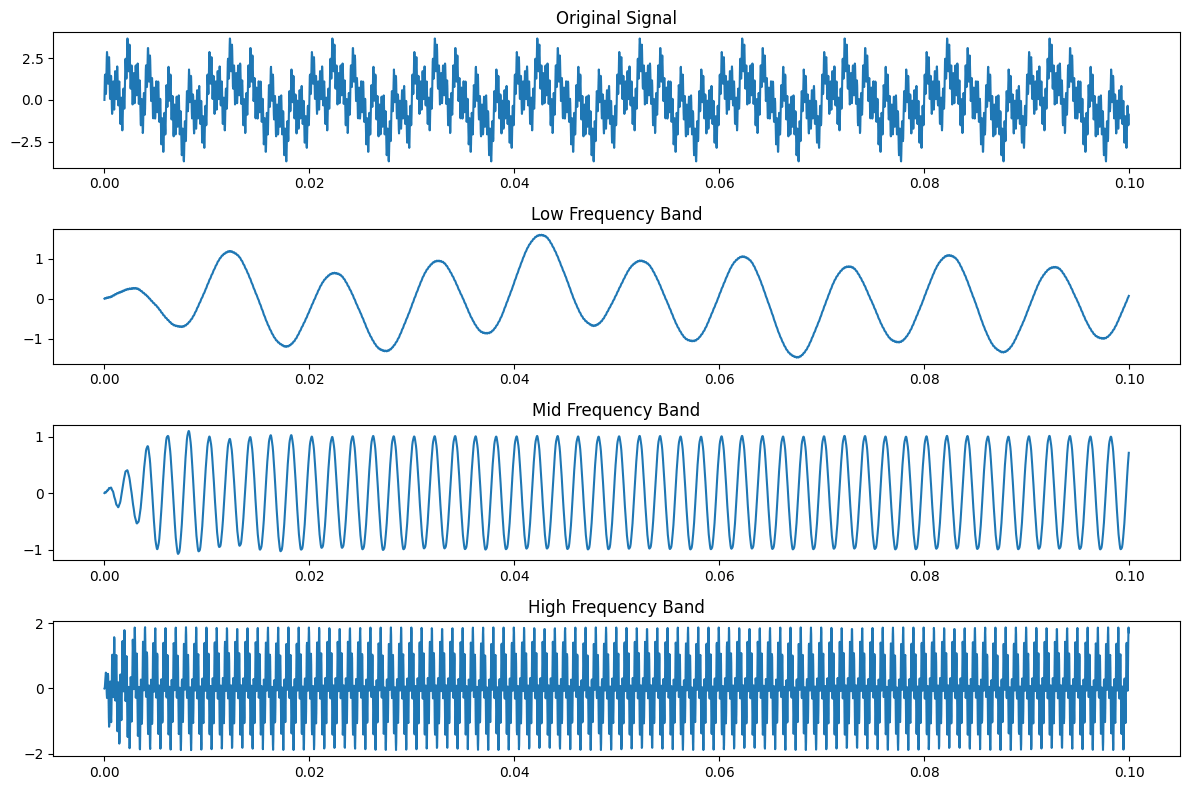
plt.figure(figsize=(12, 8))plt.subplot(4, 1, 1)
plt.title('Original Signal')
plt.plot(t, signal)plt.subplot(4, 1, 2)
plt.title('Low Frequency Band')
plt.plot(t, filtered_signal1)plt.subplot(4, 1, 3)
plt.title('Mid Frequency Band')
plt.plot(t, filtered_signal2)plt.subplot(4, 1, 4)
plt.title('High Frequency Band')
plt.plot(t, filtered_signal3)plt.tight_layout()# 绘制频谱图
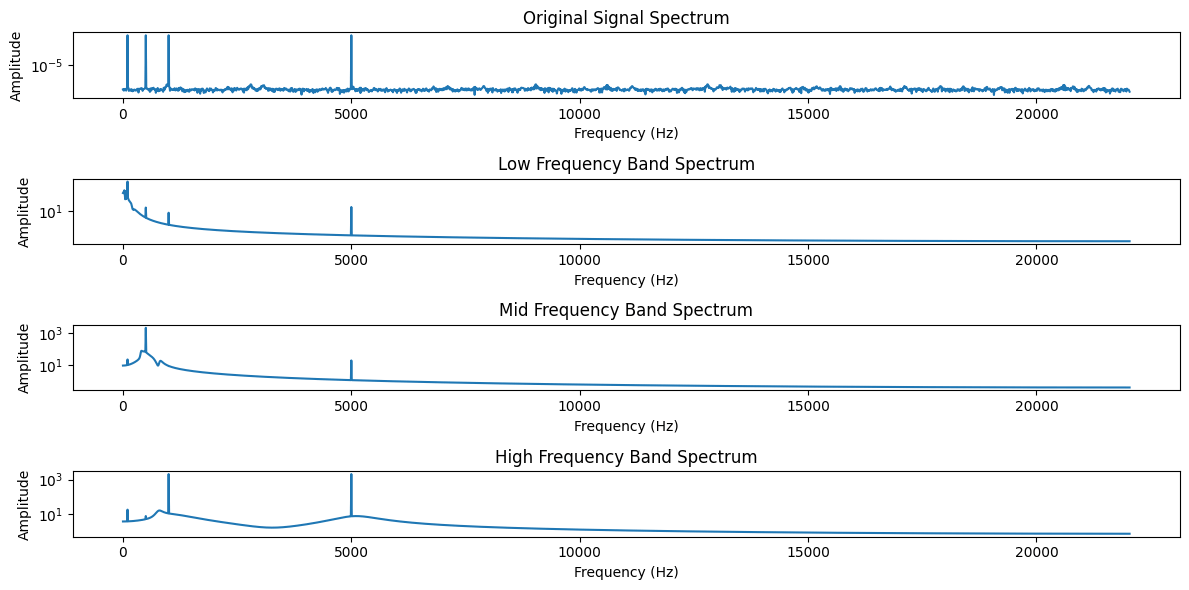
plt.figure(figsize=(12, 6))plt.subplot(4, 1, 1)
plt.title('Original Signal Spectrum')
plt.semilogy(freq_original, spec_original)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')plt.subplot(4, 1, 2)
plt.title('Low Frequency Band Spectrum')
plt.semilogy(freq_filtered1, spec_filtered1)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')plt.subplot(4, 1, 3)
plt.title('Mid Frequency Band Spectrum')
plt.semilogy(freq_filtered2, spec_filtered2)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')plt.subplot(4, 1, 4)
plt.title('High Frequency Band Spectrum')
plt.semilogy(freq_filtered3, spec_filtered3)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')plt.tight_layout()
plt.show()
输出:
公众号 | FunIO
微信搜一搜 “funio”,发现更多精彩内容。
个人博客 | blog.boringhex.top
相关文章:

椭圆滤波器
之前的文章 信号去噪 中列出了7种常用的信号去噪算法,对于后两种算法——深度学习和奇异值分解(SVD),我现在也不太理解,就先不写了。 很多朋友留言又提了一些算法,今天一起来聊聊椭圆滤波器。 椭圆滤波器(Elliptic F…...
Mac 下安装golang环境
一、下载安装包 安装包下载地址 下载完成,直接继续----->下一步到结束即可安装成功; 安装成功之后,验证一下; go version二、配置环境变量 终端输入vim ~/.zshrc进入配置文件,输入i进行编辑 打开的不管是空文本…...

前端面试大纲
一、CSS 1.说一下CSS的盒模型。 在HTML页面中的所有元素都可以看成是一个盒子 盒子的组成:内容content、内边距padding、边框border、外边距margin 盒模型的类型: 标准盒模型 margin border padding content IE盒模型 margin content(border padd…...
是一种用于在汽车和工业领域中进行通信的串行总线系统(附加案例))
CAN(Controller Area Network)是一种用于在汽车和工业领域中进行通信的串行总线系统(附加案例)
CAN(Controller Area Network)是一种用于在汽车和工业领域中进行通信的串行总线系统。它是一种高可靠性、多主机、多节点通信协议,主要用于实时控制和数据传输。 CAN数据是指在CAN总线上通过CAN协议进行通信传输的数据。CAN总线上的数据被分…...

代码随想录day53|1143.最长公共子序列、 1035.不相交的线、 53. 最大子序和
1143.最长公共子序列 dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j] 因此是if(nums1[i-1] nums2[j-1]) 1035.不相交的线 和上一题一样 53. 最大子序和 int result dp[0]; 不是0,因为dp[i]有…...
xilinx fpga ddr mig axi
硬件 参考: https://zhuanlan.zhihu.com/p/97491454 https://blog.csdn.net/qq_22222449/article/details/106492469 https://zhuanlan.zhihu.com/p/26327347 https://zhuanlan.zhihu.com/p/582524766 包括野火、正点原子的资料 一片内存是 1Gbit 128MByte 16bit …...

《golang设计模式》第三部分·行为型模式-04-迭代器模式(Iterator)
文章目录 1. 概念1.1 角色1.2 类图 2. 代码示例2.1 需求2.2 代码2.3 类图 1. 概念 迭代器(Iterator)能够在不暴露聚合体内部表示的情况下,向客户端提供遍历聚合元素的方法。 1.1 角色 InterfaceAggregate(抽象聚合)…...

python加上ffmpeg实现音频分割
前言: 这是一个系列的文章,主要是使用python加上ffmpeg来对音视频文件进行处理,包括音频播放、音频格式转换、音频文件分割、视频播放等。 系列文章链接: 链接1: python使用ffmpeg来制作音频格式转换工具(优化版) 链接2:<Python>PyQt5+ffmpeg,简单视频播放器的编写(…...

LLM之Prompt(一):5个Prompt高效方法在文心一言3.5的测试对比
在Effective Prompt: 编写高质量Prompt的14个有效方法文中我们了解了14个编写Prompt的方法(非常感谢原作者),那么这些Prompt在具体大模型中的效果如何呢?本文以百度文心一言3.5版本大模型在其中5个方法上做个测试对比。 第1条&am…...
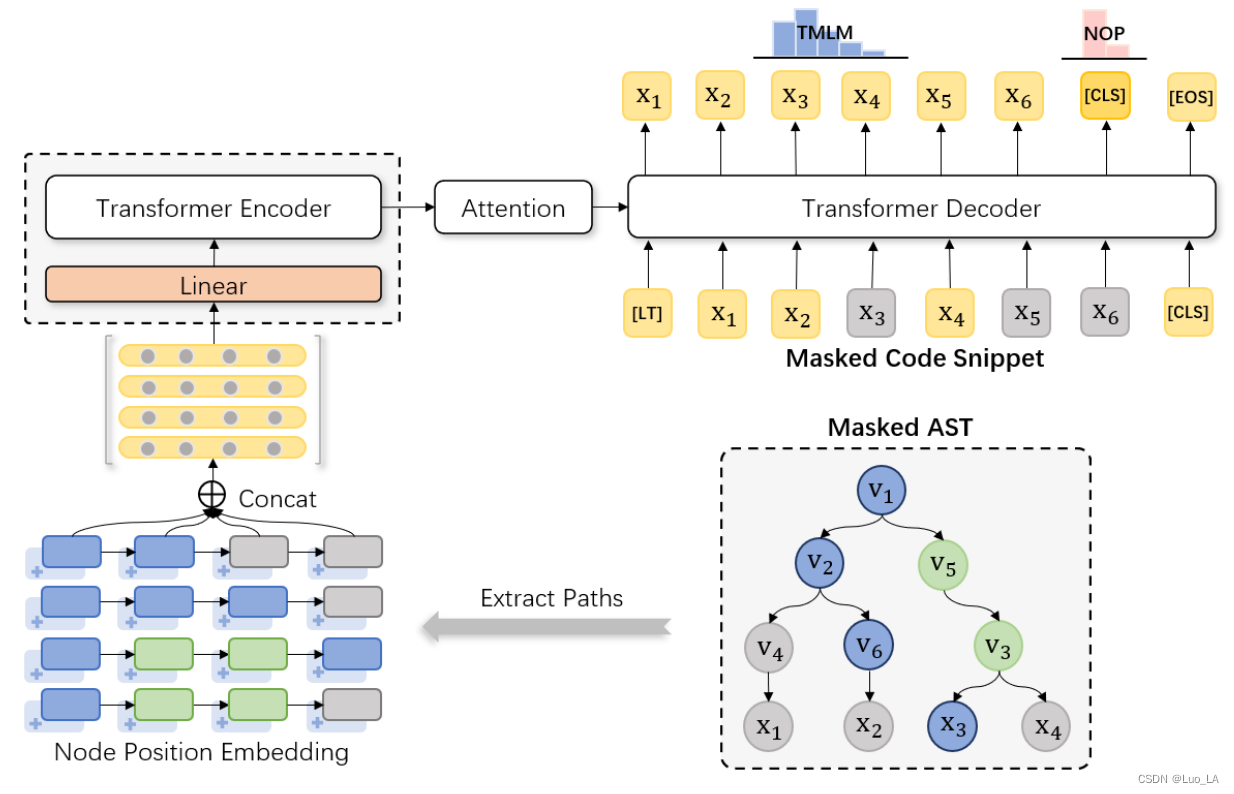
TreeBERT:基于树的编程语言预训练模型。
TreeBERT https://arxiv.org/abs/2105.12485 Comments: Accepted by UAI2021 Subjects: Machine Learning (cs.LG); Programming Languages (cs.PL) Cite as: arXiv:2105.12485 [cs.LG] 1 Introduction 现有挑战: 设计适当的机制来学习程序的语法结构 代码是强结…...
)
生成小程序的二维码的base64码(中间logo可以自定义)
1.生成基础二维码 /*** 生成微信小程序二维码,带参数,最终转成base64* param page 当前小程序相对页面 必须是已经发布的小程序存在的页面(否则报错),例如 pages/index/index, 根路径前不要填加 /,不能携带参数(参数请放在scene字段里),如果不…...

【音视频 | Ogg】Ogg封装格式详解——包含Ogg封装过程、数据包(packet)、页(page)、段(segment)等
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

ubuntu 22.04 安装ros2 iron
目录 一、镜像 二、ifconfig 三、ssh连接不上 四、安装iron 一、镜像 123云盘直接下载 二、ifconfig sudo apt install net-tools 三、ssh连接不上 sudo apt install openssh-server 四、安装iron Ubuntu (Debian packages) — ROS 2 Documentation: Iron document…...

PHP语言、B/S手术麻醉临床信息管理系统源码
手术麻醉临床信息管理系统有着完善的临床业务功能,能够涵盖整个围术期的工作,能够采集、汇总、存储、处理、展现所有的临床诊疗资料。通过该系统的实施,能够规范麻醉科的工作流程,实现麻醉手术过程的信息数字化,自动生…...
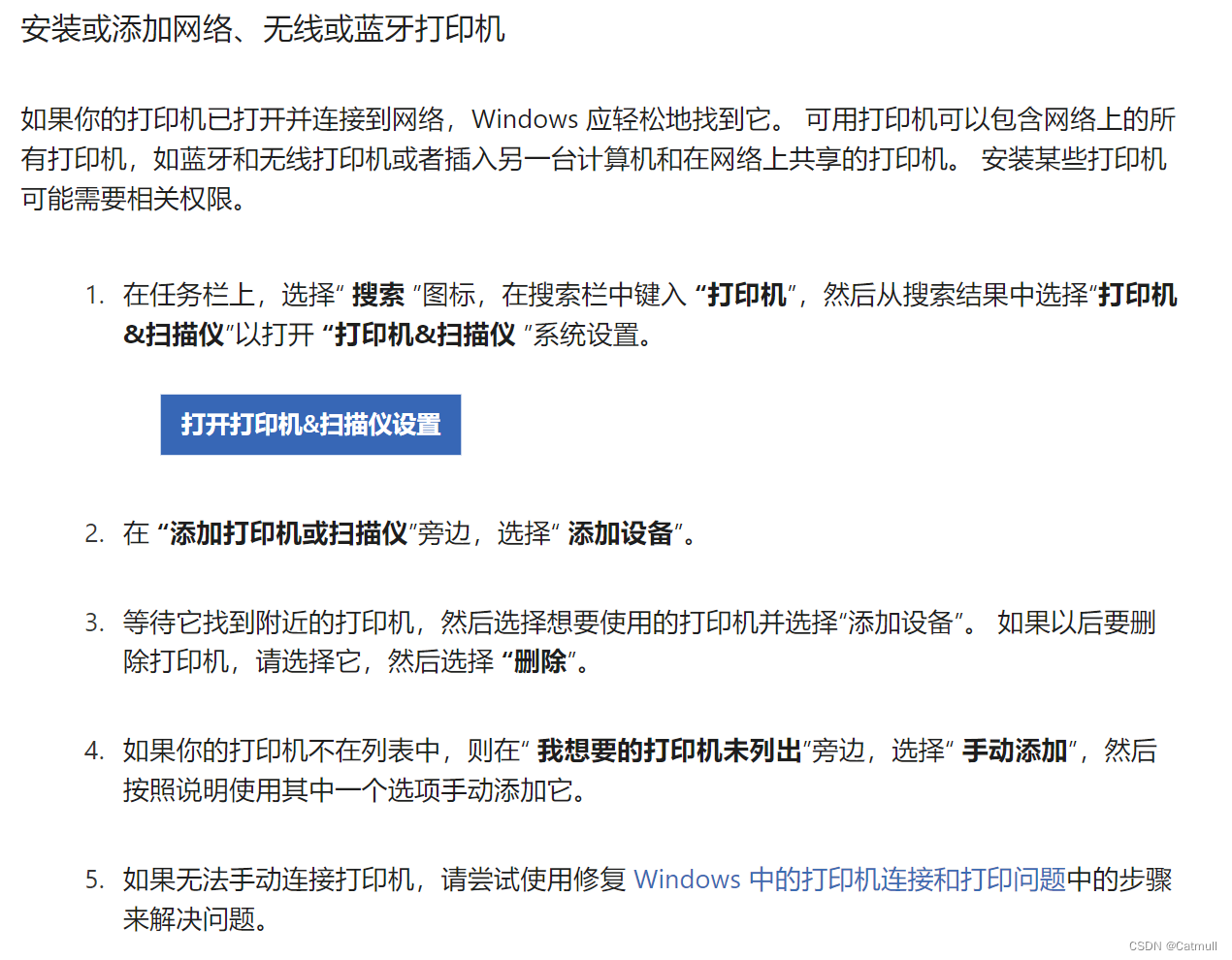
Win11安装网络打印机
https://support.microsoft.com/zh-cn/windows/%E5%9C%A8-windows-%E4%B8%AD%E5%AE%89%E8%A3%85%E6%89%93%E5%8D%B0%E6%9C%BA-cc0724cf-793e-3542-d1ff-727e4978638b...

逆向学习记录(3)工具介绍jadx、gda和jeb
1、jadx 下载地址如下,目前最新版本为v1.4.7,改成想要下载的版本号就能下载对应的版本。 https://github.com/skylot/jadx/releases/tag/v1.4.7 下载后解压,进入对应路径的bin文件夹内,运行jadx-gui.bat。 2、gda 下载地址和gi…...

C#,数值计算——偏微分方程,Mglin的计算方法与源程序
1 文本格式 using System; using System.Collections.Generic; namespace Legalsoft.Truffer { public class Mglin { private int n { get; set; } private int ng { get; set; } private double[,] uj1 { get; set; } private Lis…...

一机服务万人,拓世法宝AI智能商业数字人一体机,解锁文旅新表达
在人工智能的强劲推动下,人们走进了一个令人振奋的数字化时代。如何让文化传承与现代科技完美融合,成为一个十分有趣的议题,当AI技术结合文旅生活,便悄然开启了一种全新的旅游服务模式——AI数字文旅。 在我国国家博物馆、文旅大…...
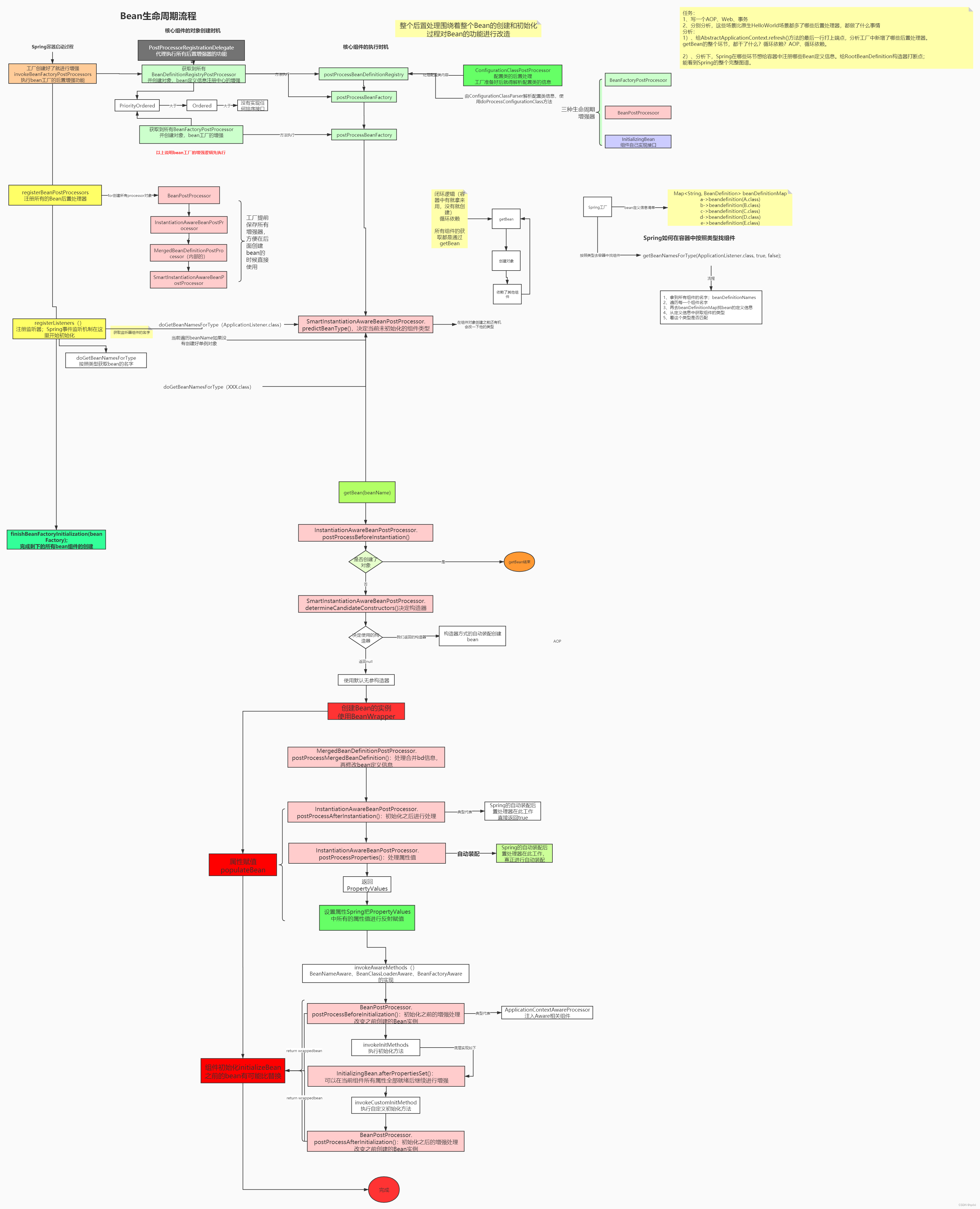
【源码解析】聊聊SpringBean是如何初始化和创建
我们知道通过类进行修复不同的属性,比如单例、原型等,而具体的流程是怎么样的呢,这一篇我们开始从源码的视角分析以下。 刷新方法 在刷新容器中有一个方法,其实就是 Bean创建的过程。 finishBeanFactoryInitialization(beanFact…...
【0基础学Java第六课】-- 数组的定义与使用
6 数组的定义与使用 6.1 什么是数组6.2 数组的创建及初始化6.2.1 数组的创建:6.2.2 数组的初始化 6.3 数组的使用6.3.1 数组中元素的访问6.3.2 Java中JVM当中的内存划分6.3.3 遍历数组 6.4 数组是引用类型6.4.1 初始JVM的内存分布6.4.2 基本类型变量与引用类型变量的…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
