周赛334(前缀和、贪心+双指针、Dijkstra求最短路径、二分答案)
文章目录
- [6369. 左右元素和的差值](https://leetcode.cn/problems/left-and-right-sum-differences/)
- 前缀和
- [6368. 找出字符串的可整除数组](https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/)
- 超长整数如何取余?
- [6367. 求出最多标记下标](https://leetcode.cn/problems/find-the-maximum-number-of-marked-indices/)
- 贪心 + 同向双指针
- 二分答案
- [6366. 在网格图中访问一个格子的最少时间](https://leetcode.cn/problems/minimum-time-to-visit-a-cell-in-a-grid/)
- Dijkstra求最短路径
- 二分答案
6369. 左右元素和的差值
难度简单4
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中:
answer.length == nums.lengthanswer[i] = |leftSum[i] - rightSum[i]|
其中:
leftSum[i]是数组nums中下标i左侧元素之和。如果不存在对应的元素,leftSum[i] = 0。rightSum[i]是数组nums中下标i右侧元素之和。如果不存在对应的元素,rightSum[i] = 0。
返回数组 answer 。
示例 1:
输入:nums = [10,4,8,3]
输出:[15,1,11,22]
解释:数组 leftSum 为 [0,10,14,22] 且数组 rightSum 为 [15,11,3,0] 。
数组 answer 为 [|0 - 15|,|10 - 11|,|14 - 3|,|22 - 0|] = [15,1,11,22] 。
示例 2:
输入:nums = [1]
输出:[0]
解释:数组 leftSum 为 [0] 且数组 rightSum 为 [0] 。
数组 answer 为 [|0 - 0|] = [0] 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= 105
前缀和
class Solution {public int[] leftRigthDifference(int[] nums) {int n = nums.length;int[] leftsum = new int[n+1];int[] rightsum = new int[n+1];for(int i = 0; i < n; i++){leftsum[i+1] = leftsum[i] + nums[i];}for(int i = n-1; i > 0; i--){rightsum[i-1] = rightsum[i] + nums[i];}int[] res = new int[n];for(int i = 0; i < n; i++){res[i] = Math.abs(leftsum[i] - rightsum[i]);}return res;}
}
6368. 找出字符串的可整除数组
难度中等4
给你一个下标从 0 开始的字符串 word ,长度为 n ,由从 0 到 9 的数字组成。另给你一个正整数 m 。
word 的 可整除数组 div 是一个长度为 n 的整数数组,并满足:
- 如果
word[0,...,i]所表示的 数值 能被m整除,div[i] = 1 - 否则,
div[i] = 0
返回 word 的可整除数组。
示例 1:
输入:word = "998244353", m = 3
输出:[1,1,0,0,0,1,1,0,0]
解释:仅有 4 个前缀可以被 3 整除:"9"、"99"、"998244" 和 "9982443" 。
示例 2:
输入:word = "1010", m = 10
输出:[0,1,0,1]
解释:仅有 2 个前缀可以被 10 整除:"10" 和 "1010" 。
提示:
1 <= n <= 105word.length == nword由数字0到9组成1 <= m <= 109
超长整数如何取余?
class Solution {// 本质就是超级长的整数如何取余public int[] divisibilityArray(String word, int m) {double x = 0; // 第 i 位 用第 i-1 位 * 10 + word[1] 表示, 来防止溢出int n = word.length();int[] res = new int[n];for(int i = 0; i < n; i++){x = (x*10 + (word.charAt(i) - '0')) % m;res[i] = (x == 0) ? 1 : 0;}return res;}
}
6367. 求出最多标记下标
难度中等17
给你一个下标从 0 开始的整数数组 nums 。
一开始,所有下标都没有被标记。你可以执行以下操作任意次:
- 选择两个 互不相同且未标记 的下标
i和j,满足2 * nums[i] <= nums[j],标记下标i和j。
请你执行上述操作任意次,返回 nums 中最多可以标记的下标数目。
示例 1:
输入:nums = [3,5,2,4]
输出:2
解释:第一次操作中,选择 i = 2 和 j = 1 ,操作可以执行的原因是 2 * nums[2] <= nums[1] ,标记下标 2 和 1 。
没有其他更多可执行的操作,所以答案为 2 。
示例 2:
输入:nums = [9,2,5,4]
输出:4
解释:第一次操作中,选择 i = 3 和 j = 0 ,操作可以执行的原因是 2 * nums[3] <= nums[0] ,标记下标 3 和 0 。
第二次操作中,选择 i = 1 和 j = 2 ,操作可以执行的原因是 2 * nums[1] <= nums[2] ,标记下标 1 和 2 。
没有其他更多可执行的操作,所以答案为 4 。
示例 3:
输入:nums = [7,6,8]
输出:0
解释:没有任何可以执行的操作,所以答案为 0 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
贪心 + 同向双指针
class Solution {// 2 3 4 5public int maxNumOfMarkedIndices(int[] nums) {Arrays.sort(nums);int res = 0;int n = nums.length;int left = 0, right = n / 2;while(left < n/2 && right < n){if(nums[left] * 2 <= nums[right]){res += 2;left++;right++;}else{right++;}}return res;}
}
二分答案
class Solution {/**二分答案:考虑匹配k对如果能匹配k对,则一定能匹配k-1对、k-2对...*/public int maxNumOfMarkedIndices(int[] nums) {Arrays.sort(nums);int left = 0, right = nums.length/2;while(left <= right){int mid = (left + right) >> 1;if(check(nums, mid)){left = mid+1;}else{right = mid-1;}}return right * 2;}public boolean check(int[] nums, int k){for(int i = 0; i < k; i++){if(nums[i] * 2 > nums[nums.length-k+i])return false;}return true;}
}
6366. 在网格图中访问一个格子的最少时间
难度困难15
给你一个 m x n 的矩阵 grid ,每个元素都为 非负 整数,其中 grid[row][col] 表示可以访问格子 (row, col) 的 最早 时间。也就是说当你访问格子 (row, col) 时,最少已经经过的时间为 grid[row][col] 。
你从 最左上角 出发,出发时刻为 0 ,你必须一直移动到上下左右相邻四个格子中的 任意 一个格子(即不能停留在格子上)。每次移动都需要花费 1 单位时间。
请你返回 最早 到达右下角格子的时间,如果你无法到达右下角的格子,请你返回 -1 。
示例 1:

输入:grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
输出:7
解释:一条可行的路径为:
- 时刻 t = 0 ,我们在格子 (0,0) 。
- 时刻 t = 1 ,我们移动到格子 (0,1) ,可以移动的原因是 grid[0][1] <= 1 。
- 时刻 t = 2 ,我们移动到格子 (1,1) ,可以移动的原因是 grid[1][1] <= 2 。
- 时刻 t = 3 ,我们移动到格子 (1,2) ,可以移动的原因是 grid[1][2] <= 3 。
- 时刻 t = 4 ,我们移动到格子 (1,1) ,可以移动的原因是 grid[1][1] <= 4 。
- 时刻 t = 5 ,我们移动到格子 (1,2) ,可以移动的原因是 grid[1][2] <= 5 。
- 时刻 t = 6 ,我们移动到格子 (1,3) ,可以移动的原因是 grid[1][3] <= 6 。
- 时刻 t = 7 ,我们移动到格子 (2,3) ,可以移动的原因是 grid[2][3] <= 7 。
最终到达时刻为 7 。这是最早可以到达的时间。
示例 2:
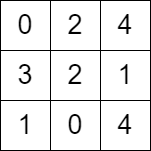
输入:grid = [[0,2,4],[3,2,1],[1,0,4]]
输出:-1
解释:没法从左上角按题目规定走到右下角。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1050 <= grid[i][j] <= 105grid[0][0] == 0
Dijkstra求最短路径
题解:https://leetcode.cn/problems/minimum-time-to-visit-a-cell-in-a-grid/solution/er-fen-da-an-bfspythonjavacgo-by-endless-j10w/
class Solution {private final static int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};public int minimumTime(int[][] grid) {int m = grid.length, n = grid[0].length;if(grid[0][1] > 1 && grid[1][0] > 1) return -1;// 否则答案一定存在(因为可以反复横跳来拖延时间)// 到达grid[i][j] 的最小时间 dis[i][j] 一定是和 (i+j) 同奇偶的// 如果到达时不同奇偶, 则+1就行int[][] dis = new int[m][n];for(int i = 0; i < m; i++){Arrays.fill(dis[i], Integer.MAX_VALUE);}dis[0][0] = 0;PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> a[0]-b[0]);pq.add(new int[]{0,0,0});while(true){int[] poll = pq.poll();int d = poll[0], i = poll[1], j = poll[2];if(i == m-1 && j == n-1) return d;for(int[] dir : dirs){ // 枚举周围四个格子int x = i + dir[0], y = j + dir[1];if(x >= 0 && x < m && y >= 0 && y < n){int nd = Math.max(d+1, grid[x][y]);nd += (nd-x-y) % 2; // nd 必须和 x+y 同奇偶if(nd < dis[x][y]){dis[x][y] = nd; // 更新最短路pq.add(new int[]{nd, x, y});}}}}}
}
二分答案
二分到终点的时间,然后跑 BFS
如果可以从终点到达起点,说明可以在大于 endTime 的时刻到达终点;反之,如果无法从终点到达起点,说明无法在小于 endTime 的时刻到达终点。
有单调性,可以二分到达终点的时间。
class Solution {private final static int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};private int[][] grid, vis;public int minimumTime(int[][] grid) {int m = grid.length, n = grid[0].length;if (grid[0][1] > 1 && grid[1][0] > 1) // 无法「等待」return -1;this.grid = grid;vis = new int[m][n];int left = Math.max(grid[m - 1][n - 1], m + n - 2) - 1;int right = (int) 1e5 + m + n; // 开区间while (left + 1 < right) {int mid = (left + right) >>> 1;if (check(mid)) right = mid;else left = mid;}return right + (right + m + n) % 2;}private boolean check(int endTime) {int m = grid.length, n = grid[0].length;vis[m - 1][n - 1] = endTime;var q = new ArrayList<int[]>();q.add(new int[]{m - 1, n - 1});for (int t = endTime - 1; !q.isEmpty(); --t) {var tmp = q;q = new ArrayList<>();for (var p : tmp) {int i = p[0], j = p[1];for (var d : dirs) { // 枚举周围四个格子int x = i + d[0], y = j + d[1];if (0 <= x && x < m && 0 <= y && y < n && vis[x][y] != endTime && grid[x][y] <= t) {if (x == 0 && y == 0) return true;vis[x][y] = endTime; // 用二分的值来标记,避免重复创建 vis 数组q.add(new int[]{x, y});}}}}return false;}
}
if (0 <= x && x < m && 0 <= y && y < n && vis[x][y] != endTime && grid[x][y] <= t) {if (x == 0 && y == 0) return true;vis[x][y] = endTime; // 用二分的值来标记,避免重复创建 vis 数组q.add(new int[]{x, y});}}}}return false;
}
}
相关文章:

周赛334(前缀和、贪心+双指针、Dijkstra求最短路径、二分答案)
文章目录[6369. 左右元素和的差值](https://leetcode.cn/problems/left-and-right-sum-differences/)前缀和[6368. 找出字符串的可整除数组](https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/)超长整数如何取余?[6367. 求出最多标记下标](ht…...

imx6ull——I2C驱动
I2C基本介绍 SCL 为高电平,SDA 出现下降沿:起始位 SCL 位高电平,SDA出现上升沿:停止位 主机——从机地址(ack)——寄存器地址(ack)——数据(ack) 重点:先是写,…...
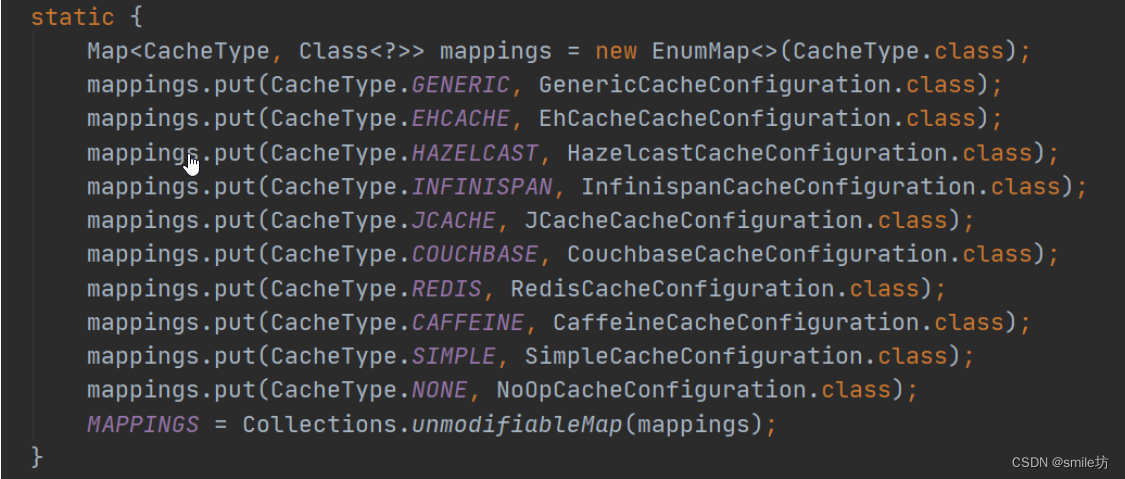
Spring Cache的基本使用与分析
概述 使用 Spring Cache 可以极大的简化我们对数据的缓存,并且它封装了多种缓存,本文基于 redis 来说明。 基本使用 1、所需依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-…...
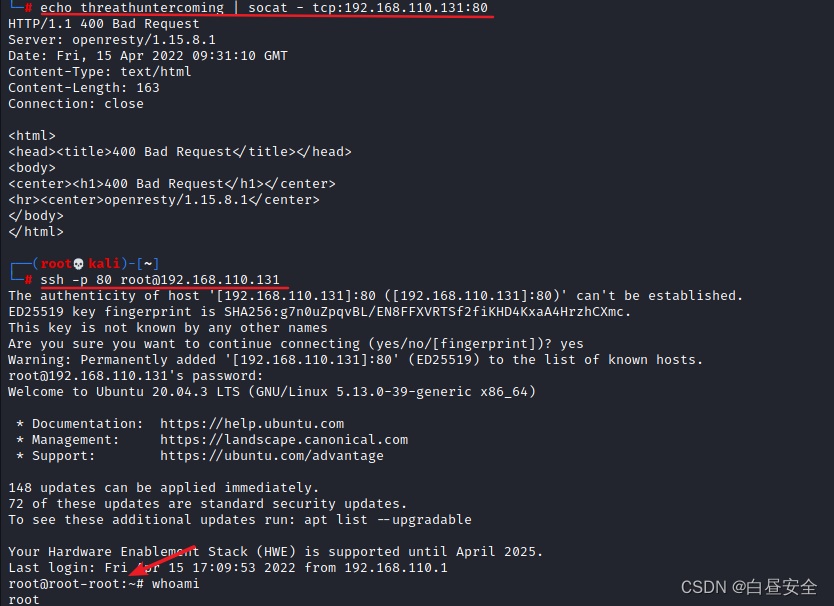
【安全知识】——端口复用隐藏后门
作者名:白昼安全主页面链接: 主页传送门创作初心: 以后赚大钱座右铭: 不要让时代的悲哀成为你的悲哀专研方向: web安全,后渗透技术每日鸡汤: 精彩的人生是在有限的生命中实现无限价值端口复用是…...

Tina_Linux量产测试使用指南_new
OpenRemoved_Tina_Linux_量产测试_使用指南_new 1 概述 文档主要描述如何配置tinatest 并搭建量产测试环境。 1.1 编写目的 • 介绍量产配置方法; • 介绍量产测试环境搭建流程; • 介绍如何使用dragonMAT 软件; • 方便开发人员按照说明…...
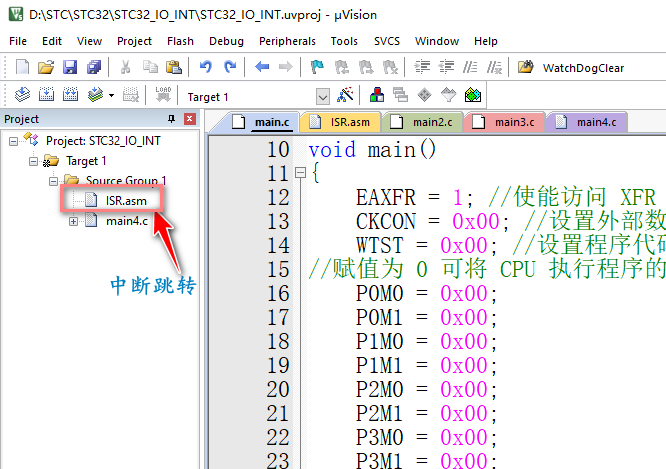
STC32单片机 普通 I/O 口中断功能介绍和使用
STC32单片机 普通 I/O 口中断功能和使用✨STC32单片机普通 I/O 口中断,不是传统外部中断. 🔖手册上描述:STC32G 系列支持所有的 I/O 中断,且支持 4 种中断模式:下降沿中断、上升沿中断、低电平中断、高电平中断。每组 …...

计算机学生如何找到第一份实习?
作为一名计算机专业的学生,找到第一份实习是非常重要的一步,它不仅可以帮助你更好地了解行业,增加实践经验,还可以为即将到来的校招提供有力支持。计算机专业的校招,每年都在变得越来越卷。5年前,可能你只要…...

《Python机器学习》基础代码
1,要学习Python机器学习,第一步就是读入数据,这里我们以读入excel的数据为例,利用jupyter notebook来编码,具体教程看这个视频 推荐先上传到jupyter notebook,再用名字.xlsx来导入 Jupyter notebook导入Excel数据的两种方法介绍_哔哩哔哩_bilibili 2,…...

【前端】JS异步加载
文章目录为什么要异步加载如何实现异步加载参考为什么要异步加载 两个原因其实是一个意思。 原因1: JS是单线程的语言,它会同步的执行代码,从上往下执行 但是,一旦网络不好,或要加载的js文件过大的话,会…...

【MySQL】SQL语言的五个部分
DQL 数据查询语言(Data Query Language,DQL):DQL主要用于数据的查询,其基本结构是使用SELECT子句,FROM子句和WHERE子句的组合来查询一条或多条数据。 DML 数据操作语言(Data Manipulation La…...

详细的IO面试题汇总
IO 流简介 IO 即 Input/Output,输入和输出。数据输入到计算机内存的过程即输入,反之输出到外部存储(比如数据库,文件,远程主机)的过程即输出。数据传输过程类似于水流,因此称为 IO 流。IO 流在…...

在Linux终端管理你的密码!
大家好,我是良许。 现在是互联网时代,我们每天都要跟各种 APP 、网站打交道,而这些东西基本上都需要注册才可以使用。 但是账号一多,我们自己都经常记不清对应的密码了。有些小伙伴就一把梭,所有的账号密码都是一样。…...
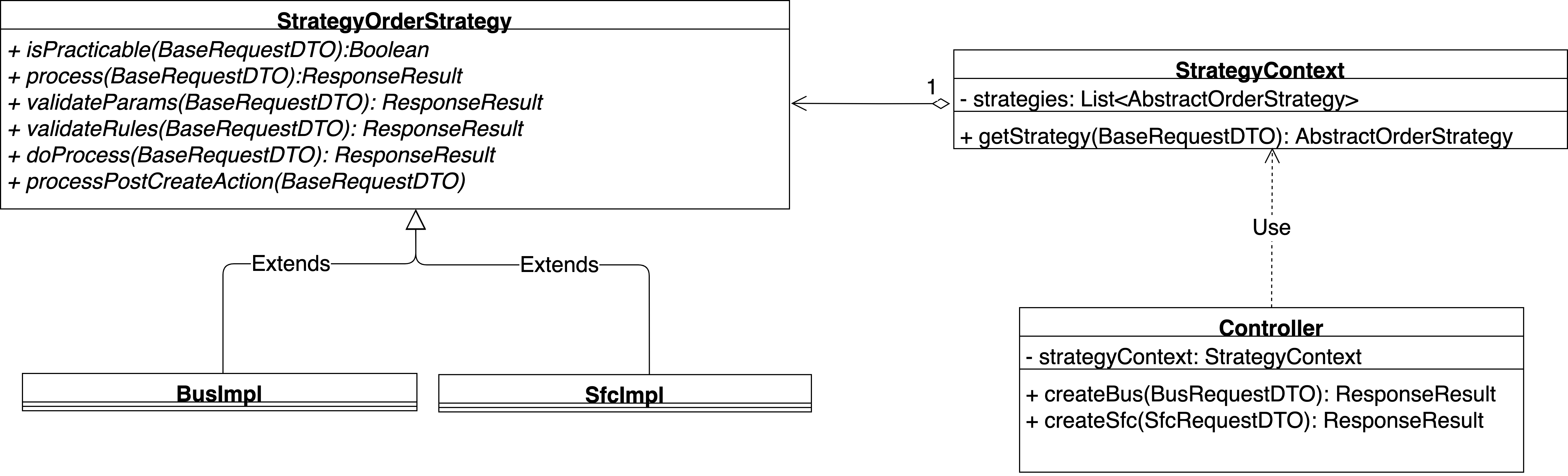
【设计模式】策略模式在Java工程中应用
在之前的文章中,曾经给大家介绍过策略模式:【设计模式】策略模式,在该篇文章中,我们曾很清楚的说到,策略模式主要解决的问题是:在有多种算法相似的情况下,解决使用 if...else 所带来的复杂和难以…...

Linux驱动开发工程师需要掌握哪些技能?
一、前言 Linux驱动开发是一项高度技术性的工作,需要深厚的编程技能和对计算机硬件的深入理解。随着物联网、人工智能等领域的快速发展,Linux驱动开发工程师的需求日益增加。在这篇文章中,我将为您介绍一条Linux驱动开发工程师的学习路线&am…...
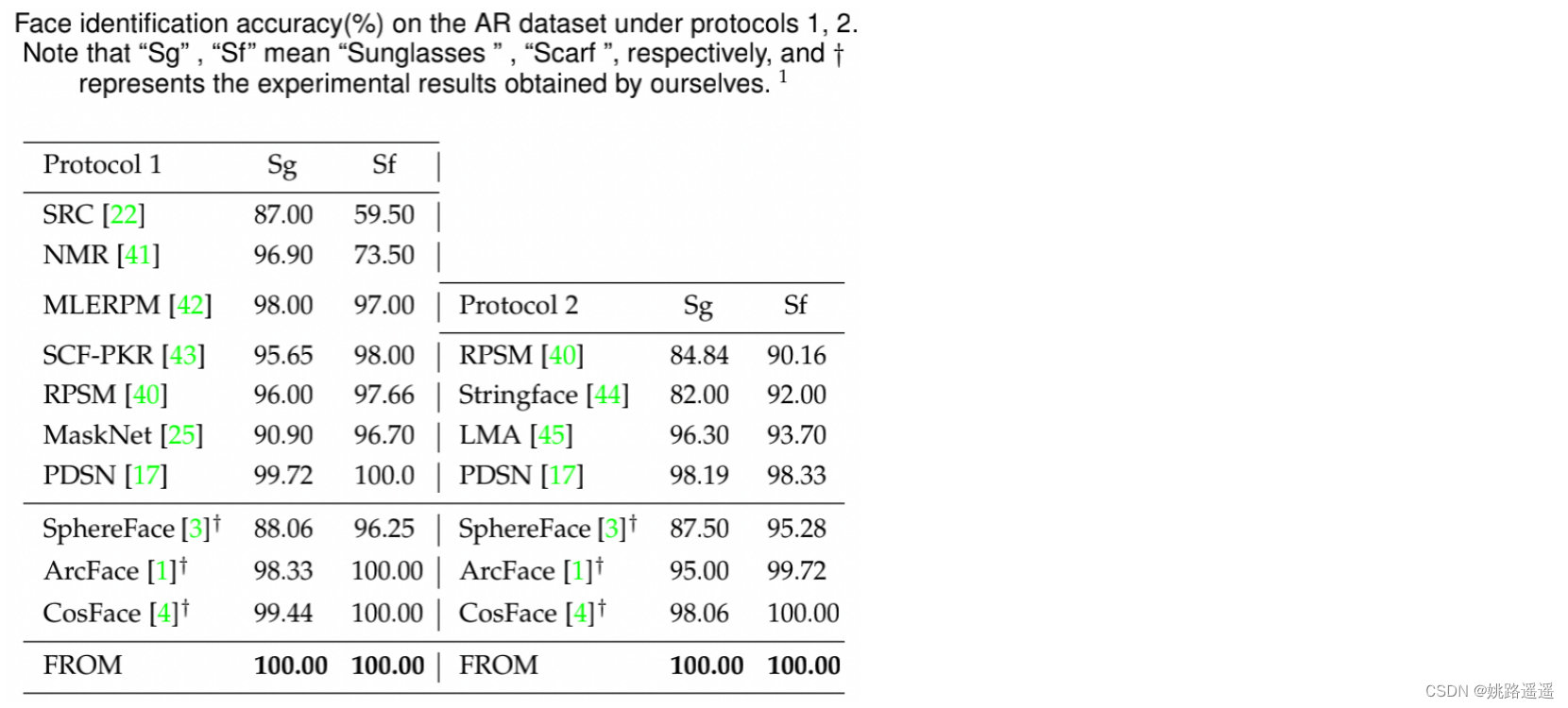
【人脸识别】FROM:提升遮挡状态下的人脸识别效果
论文题目:《End2End Occluded Face Recognition by Masking Corrupted Features》 论文地址:https://arxiv.org/pdf/2108.09468v3.pdf 代码地址:https://github.com/haibo-qiu/from 1.前言 人脸识别技术已经取得了显著的进展,主要…...

浏览器缓存
什么是缓存? 当第一次访问网站的时候,比如www.baidu.com,电脑会图片,文件等下载下来,当第二次访问网站的时候,网站就会直接被加载出来. 缓存的好处? 减轻服务器压力,减少请求的放松.提高性能,在本地打开资源肯定比在服务器上获取要快减少宽带的消耗,当我们使用缓存时,只会…...

【软考 系统架构设计师】论文范文③ 论数据访问层设计技术及其应用
>>回到总目录<< 文章目录 论数据访问层设计技术及其应用范文摘要正文论数据访问层设计技术及其应用 在信息系统的开发与建设中,分层设计是一种常见的架构设计方法,区分层次的目的是为了实现“高内聚低耦合”的思想。分层设计能有效简化系统复杂性,使设计结构清…...

802.11 MCS 的最低SNR分析
常常看到这样的表格: 那么这个SNR如何而来? 看看RSSI和SNR的关系,它们之间隔了一个noise floor。从表格看得出,这个底噪在-80~-90之间。 而SNR的核心,也有类似的原因,它和BER有关。...

用于C++的对象关系映射库—YB.ORM
1 介绍YB.ORM YB.ORM 旨在简化与关系数据库交互的 C 应用程序的开发。 对象关系映射器(ORM) 通过将数据库表映射到类并将表行映射到应用程序中的对象来工作,这种方法可能不是对每个数据库应用程序都是最佳的,但它被证明在需要复杂逻辑和事务处理的应用程…...
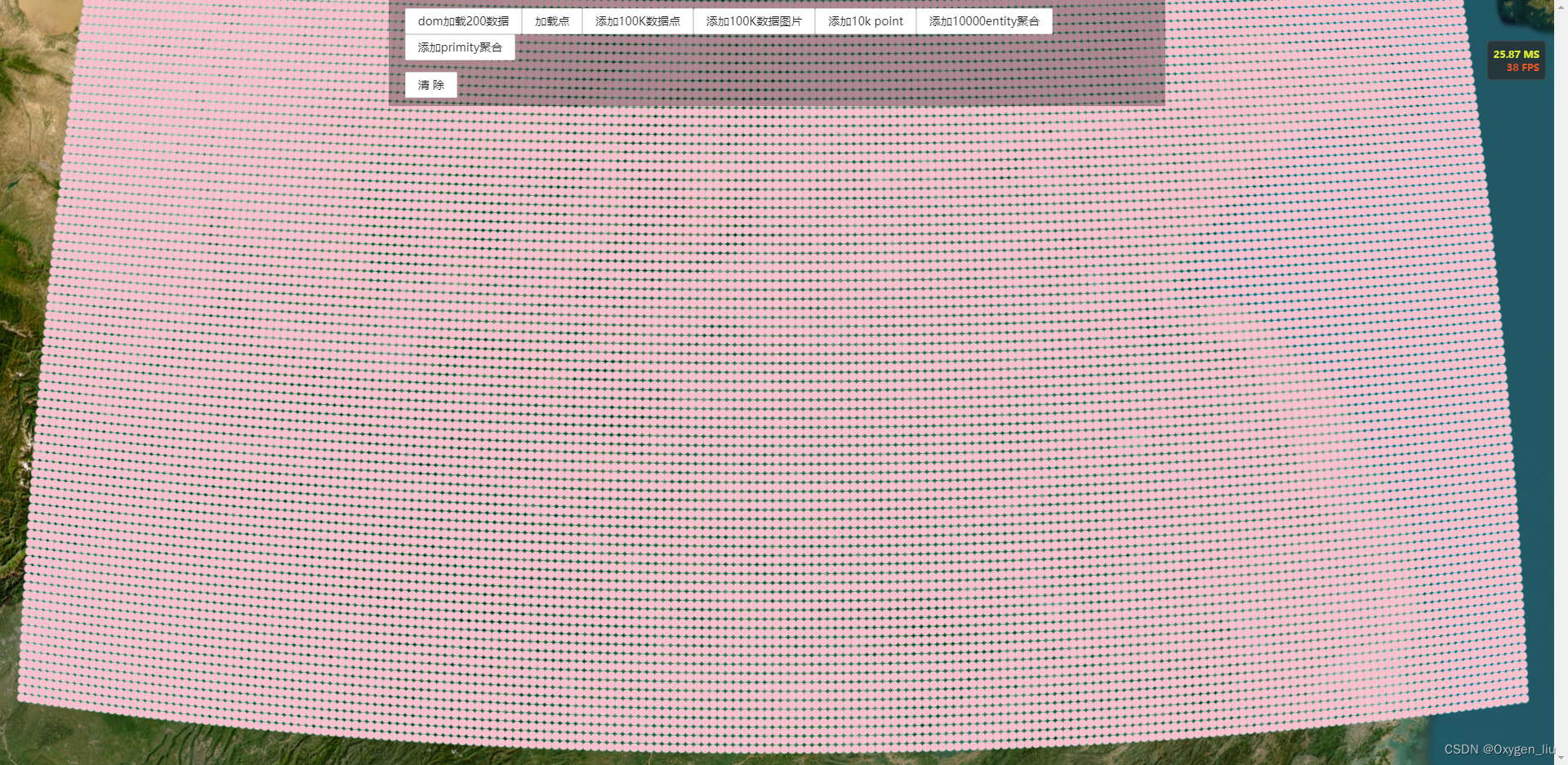
Cesium 100K数据加载 支持弹窗 动态更改位置
前言:今天总结关于point、label、billboard海量数据加载。后续会研究下大量model加载以及大bim(几百G上T)模型记载 海量点加载 弹窗 加载点位时,不加载弹窗。点击点位时在加载弹窗,及有效的减少加载量,优化性能。 const handler …...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
