【数据结构】时间复杂度和空间复杂度以及相关OJ题的详解分析

📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:数据结构
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 1.算法效率
- 1.1 如何衡量一个算法的好坏:
- 1.2 算法的复杂度
- 2.时间复杂度
- 2.1 什么是时间复杂度
- 2.2 大O渐进表示法 (估算)
- 2.3 常见的时间复杂度计算举例
- 2.3.1 实例1:
- 2.3.2 实例2:
- 2.3.3 实例3:
- 2.3.4 实例4
- 2.3.5 实例5:
- 2.3.6 实例6:
- 2.3.7 实例7:
- 2.3.8 实例8
- 2.4 常见的复杂度对比
- 3.根据对时间复杂度的要求编写代码
- 3.1 消失的数字
- 3.2 轮转数组
- 4.空间复杂度
- 4.1 什么是空间复杂度
- 4.2 常见的空间复杂度计算举例
- 4.2.1 实例1:
- 4.2.2 实例2:
- 4.2.3 实例3:
- 4.2.4 实例4:
- 5.根据对空间复杂度的要求编写代码
- 5.1 移除元素
- 6.总结:
学习顺序
插入排序->选择排序->交换排序->归并排序->非比较排序->文件排序
1.算法效率
1.1 如何衡量一个算法的好坏:
递归代码 ———— 斐波那契数列的代码量十分简洁,所以这个算法是很好的?但其实使用递归是不太好,计算第40位斐波那契数时要很长时间,原因是内部产生大量重复的计算。那该如何去衡量算法的优劣呢?
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int Fib(int n)
{if(n > 2)return Fib(n - 1) + Fib(n - 2);elsereturn 1;
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("第%d个斐波那契数是%d\n", n, ret);return 0;
}1.2 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。
衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。
所以对空间复杂度比较在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注算法的空间复杂度。
2.时间复杂度
2.1 什么是时间复杂度
算法的时间复杂度是一个函数,它描述了该算法的运行时间。
一个算法所花费的时间与其中语句的执行次数成正比,所以算法中的基本操作的执行次数,为算法的时间复杂度。即找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
//计算fun1中++count语句总共执行了多少次
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i) {for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count; }int M = 10;while (M--) {++count; }printf("%d\n", count);
}
分析:
从上述代码中可以看出Func1的时间复杂度函数为F(N) = N * N + 2 * N + 10
▶ N = 10 F(N) = 130
▶ N = 100 F(N) = 10210
▶ N = 1000 F(N) = 1002010
从上述就可以看出N越大,对结果的影响就越小。实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法 (估算)
2.2 大O渐进表示法 (估算)
大O符号 (Big O notation):用于描述函数渐近行为的数学符号
推导大O阶的方法:
1.用常数1取代运行时间中的所有加法常数
2.在修改后的运行次数函数中,只保留最高项3. 如果最高阶项存在且系数不是1,则去除与这个项相乘的系数,得到的结果就是大O阶
另外有些算法的时间复杂度存在最好,平均和最坏情况,例如:在一个长度为N的数组中查找一个数据X,最好的情况1次就找到;平均的情况N/2就找到;最坏的情况N次才找到
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
对于上面的Func1函数,使用大O的渐近表示法后,时间复杂度为O(N^2)
▶ N = 10 F(N) = 100
▶ N = 100 F(N) = 10000
▶ N = 1000 F(N) = 1000000
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3 常见的时间复杂度计算举例
2.3.1 实例1:
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
分析:
Func2的时间复杂度函数为F(N) = (2N + 10)
使用大O渐近表示法:保留影响最大的一项、去掉系数则为O(N)
2.3.2 实例2:
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
分析:
Func3的时间复杂度函数为F(N) = (M + N)
使用大O渐近表示法:不一定只有一个未知数,所以这里可以写O(M + N)
也可以写成如下:
▶ O(max(M, N)):取M和N的较大值
▶ O(M):如果能说明M远大于N
▶ O(N):如果能说明N远大于M
▶ O(N)/O(M):如果能说明M和N差不多大
2.3.3 实例3:
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);}
分析:
Func4的时间复杂度函数为F(N) = (100)
使用大O渐近表示法:使用1代表常数,所以O(1)
2.3.4 实例4
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
分析:
这是冒泡排序的一个优化版本,在一趟排序的过程中如果没有交换数据的话,它就会跳出循环
BubbleSort的时间复杂度函数为F(N) = ((n - 1) + (n - 2) … + 2 + 1)
发现这是一个等差数列,利用公式整合得:F(N) = n * n / 2 -> F(N) = N^2 / 2
使用大O渐近表示法:
(最坏情况):O(N^2) ->N^2的数量级
(平均情况):O(N^2) -> N^2 / 2
(最好情况):O(N)->只是比较了N-1次,本身就有序的时候
2.3.5 实例5:
//二分查找,折半查找(数组有序)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;while (begin < end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}
分析:
BinarySearch依然存在最好、平均、最坏的情况:
BinarySearch的时间复杂度函数为F(N) = N / 2 / 2 / 2 … /2 = 1
使用大O渐近表示法:O(log₂N)或O(logN) -> 因为底数不好打出来,有时候一般也这样写
x:N / 2^x = 1 -> N = 2^x -> log₂N = x
(最坏情况):O(logN) ->找了一遍
(最好情况):O(1)->在中间位置
2.3.6 实例6:
long long Fac(size_t N)
{if(0 == N)return 1;//0!=1 阶乘return Fac(N-1)*N;
}
每个里面是常数次,总共递归了n+1次
分析:
Fac的时间复杂度为F(N) = (N+1)
使用大O渐近表示法:O(N)
2.3.7 实例7:
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
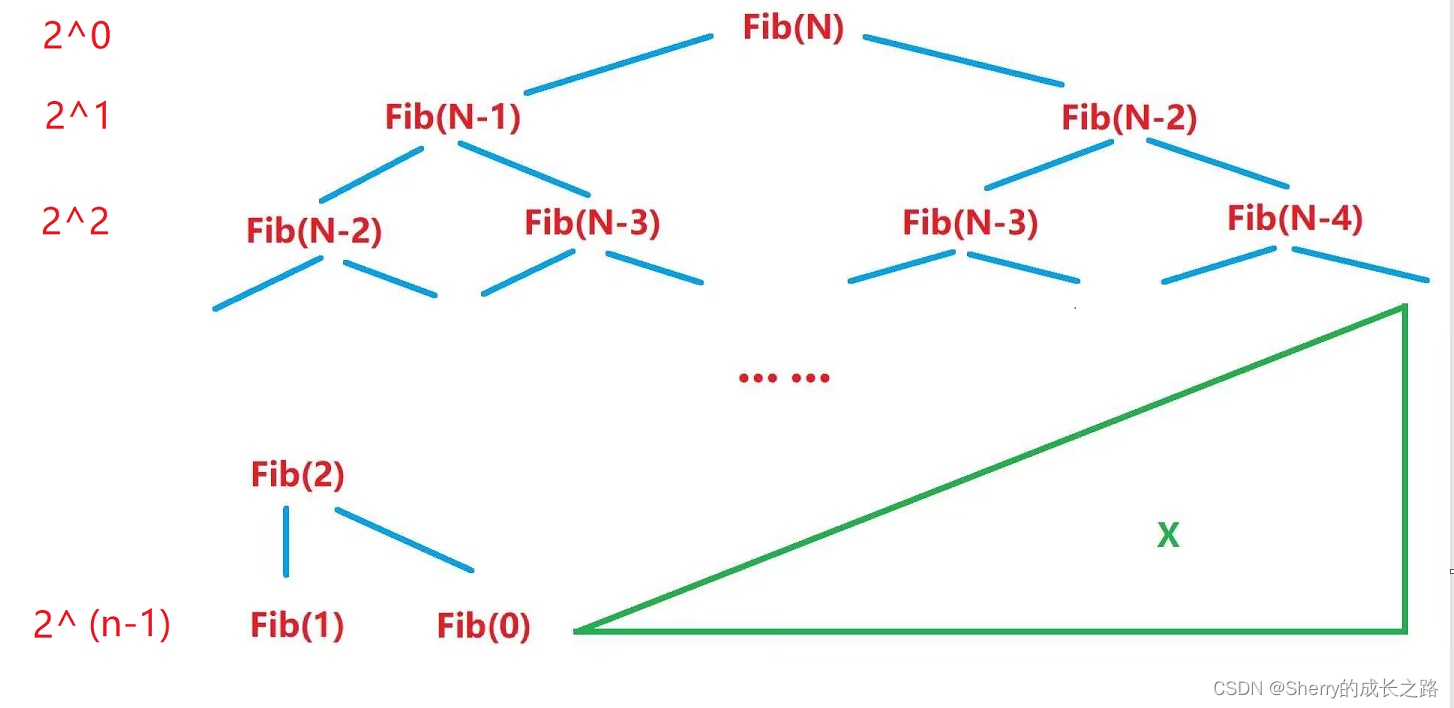
分析:
2^0 + 2^1 + 2^2 + 2^3 … +2^(N-3) + 2^(N-2)+ 2^(N-1)=等比数列-缺少常数
使用大O渐近表示法:O(2^N)
2.3.8 实例8
//计算strchr的时间复杂度
const char*strchr(const char*str,int character)while(*str)
{if(*str==character)return str;str++;
}
时间复杂度为O(N)
2.4 常见的复杂度对比
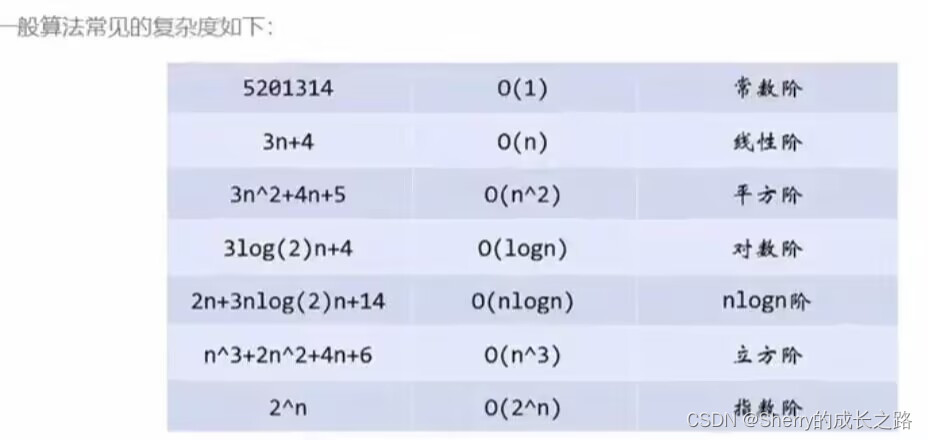
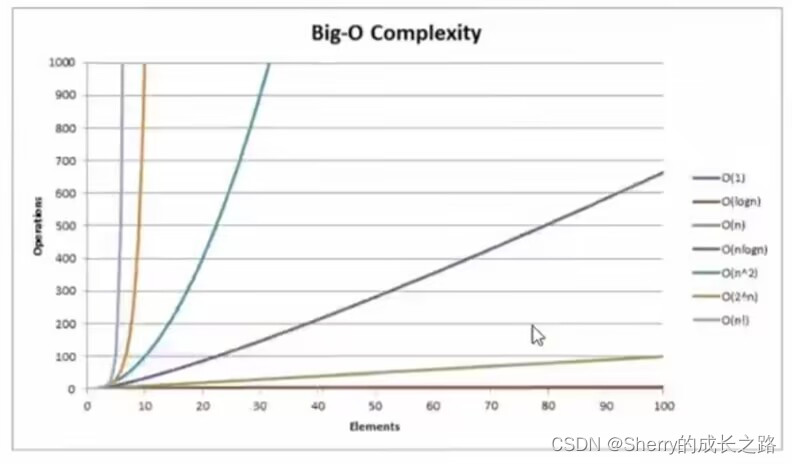
3.根据对时间复杂度的要求编写代码
3.1 消失的数字
17.04. 消失的数字
题述:数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
示例 1: ---------- 示例 2:
输入:[3,0,1] ----- 输入:[9,6,4,2,3,5,7,0,1]
输出:2 ----------- 输出:8
核心思想:
方法一:先排序,再依次判断第1个数和之后的数相加是否等于第3个数,若不等,则它们的和就是缺失的数————冒泡排序时间复杂度O(N²),快速排序时间复杂度O(N*log₂N)
方法二:求和,如果有n个数,则0+1+2…+n,最后整体再减去数组中的值的累加就是缺失的数————时间复杂度O(N)
方法三:异或,使用0跟0—n之间的数异或,再跟数值中的值异或,异或的结果就是缺失的数
方法二
IO型:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int FindNum1(int arr[], int n)
{int i = 0;//把n+1个数加起来,放在sum里int sum = 0;for (i = 0; i < n + 1; i++){sum += i;}//再减去数组里的数,结果就是缺失的数for (i = 0; i < n; i++){sum -= arr[i];}return sum;
}
int main()
{int arr[20] = { 0 };//规定输入有n个数int n = 3;int i = 0;for (i = 0; i < n; i++){scanf("%d", &arr[i]);}int ret = FindNum1(arr, n);printf("%d\n", ret);return 0;
}
方法三
IO型:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int FindNum2(int arr[], int n)
{int i = 0;//把n+1个数异或后,放在sum里int val = 0;for (i = 0; i < n + 1; i++){val ^= i;}//再和数组里的异或,剩下的就是缺失的数for (i = 0; i < n; i++){val ^= arr[i];}return val;
}
int main()
{int arr[20] = { 0 };//n个数int n = 3;int i = 0;for (i = 0; i < n; i++){scanf("%d", &arr[i]);}int ret = FindNum2(arr, n);printf("%d\n", ret);return 0;
}
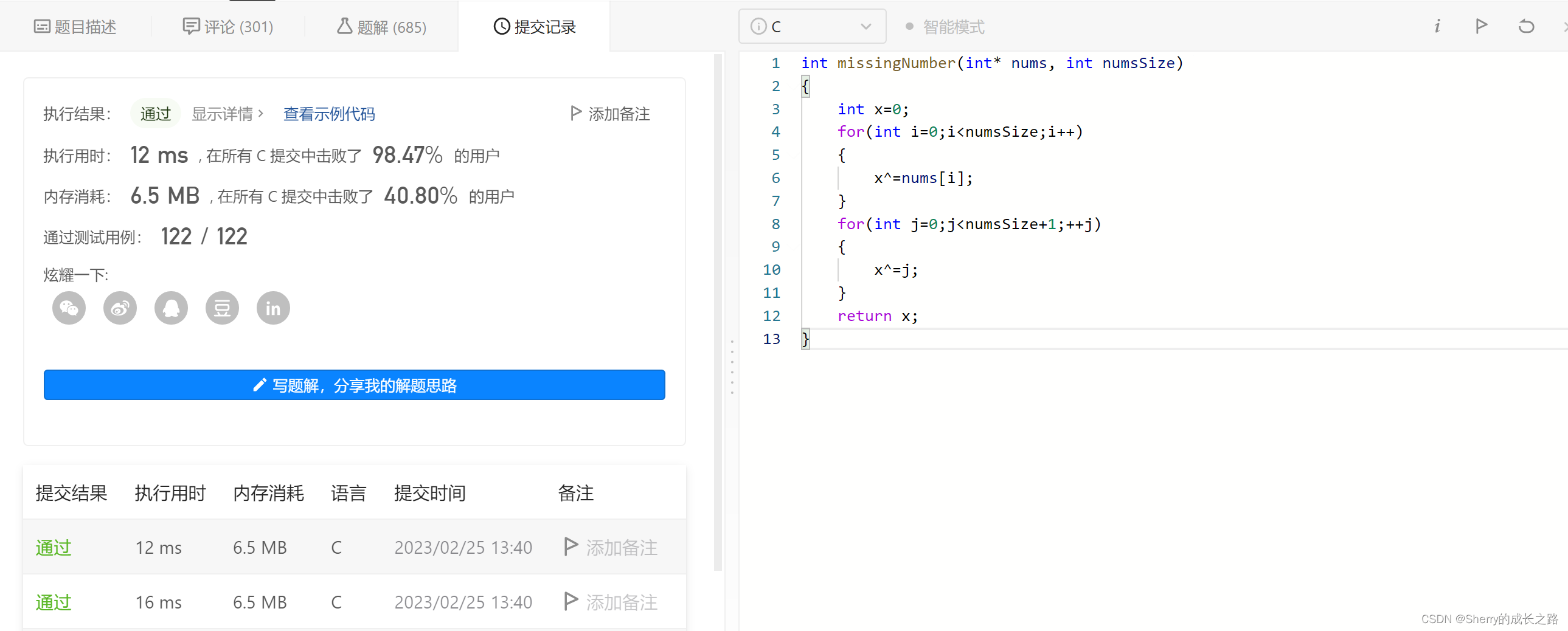
接口型:
int missingNumber(int* nums, int numsSize)
{int x=0;for(int i=0;i<numsSize;i++){x^=nums[i];}for(int j=0;j<numsSize+1;++j){x^=j;}return x;
}
3.2 轮转数组
189. 轮转数组
题述:给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。要求时间复杂度O(N)
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
核心思想:
方法一:这是1个字符的旋转,拷贝一份最右值,数组中的值都向右挪劫1次,再把拷贝的内容放在开头;在外面套一层循环就可以旋转k个字符了————时间复杂度O(N²)
分析:O(k*N)最坏情况下 k为N-1或N-1的倍数->O(N²)
方法二:空间换时间————时间复杂度O(N),空间复杂度O(N)
方法三:三步翻转法————时间复杂度O(N),空间复杂度O(N)–调用一个栈帧
方法二
IO型:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
#include<assert.h>
char* Rotate1(const char* arr, int len, int k, char* temp)
{assert(arr && temp);//拷贝一份新空间的首地址用于返回char* tem = temp;//我们当前写的这个代码是不适用于旋转的字符k大于目标数组的arr,所以如果k大于arr时,我们需要看看k有几个arr,并把它排除掉k %= len;int i = 0;//先拷贝后半部分的字符for (i = len - k; i < len; i++){*temp = *(arr + i);temp++;}//再拷贝前半部分的字符for (i = 0; i < len - k; i++){*temp = *(arr + i);temp++;}return tem;
}
int main()
{//temp为新的空间char temp[20] = { 0 };//arr存储要旋转的字符串char arr[20] = { 0 };gets(arr);//旋转k个字符int k = 0;scanf("%d", &k);char* ret = Rotate1(arr, strlen(arr), k, temp);printf("%s\n", ret);return 0;
}
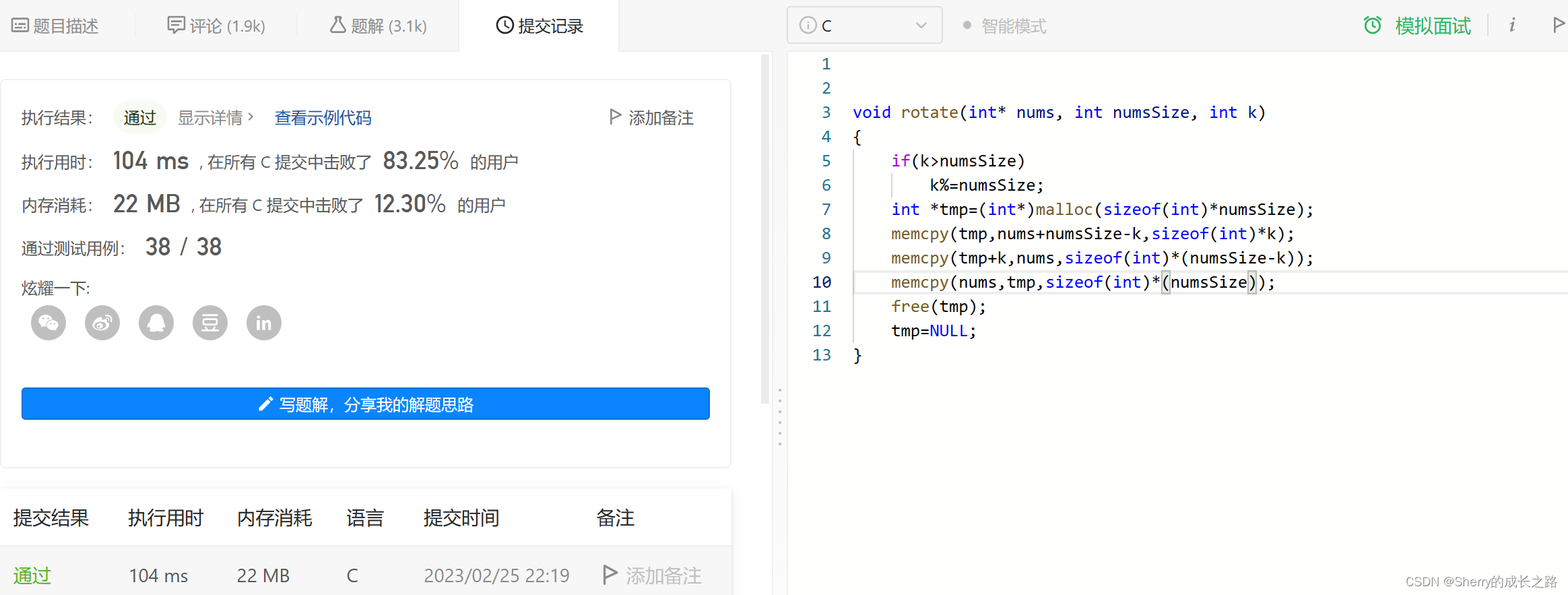
接口型:
void rotate(int* nums, int numsSize, int k)
{if(k>numsSize)k%=numsSize;int *tmp=(int*)malloc(sizeof(int)*numsSize);memcpy(tmp,nums+numsSize-k,sizeof(int)*k);memcpy(tmp+k,nums,sizeof(int)*(numsSize-k));memcpy(nums,tmp,sizeof(int)*(numsSize));free(tmp);tmp=NULL;
}
方法三
IO型:
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<assert.h>
#include<string.h>
void reverse(char* left, char* right)
{assert(left && right);while (left < right){char temp = *left;*left = *right;*right = temp;left++;right--;}
}
void string_right_rotation(char* str, int k)
{assert(str);int len = strlen(str);//我们当前写的这个代码是不适用于旋转的字符k大于目标数组的arr,所以如果k大于arr时,我们需要看看k有几个arr,并把它排除掉k %= len;reverse(str, str + (len - k - 1));//第一部分reverse(str + (len - k), str + len - 1);//第二部分reverse(str, str + len - 1);//整体
}
int main()
{//arr存储要旋转的字符串char arr[20] = { 0 };gets(arr);//旋转k个字符int k = 0;scanf("%d", &k);string_right_rotation(arr, k);printf("%s\n", arr);return 0;
}
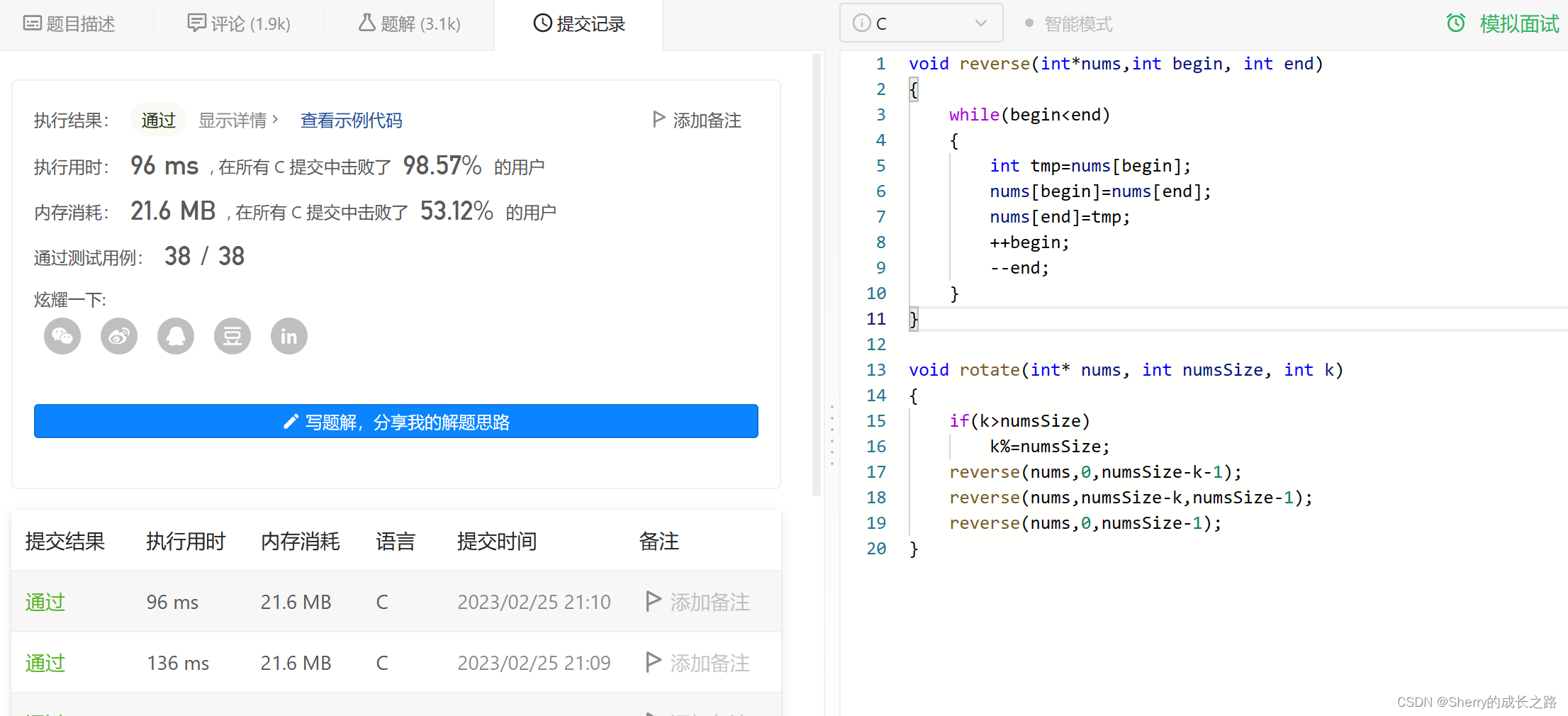
接口型:
void reverse(int*nums,int begin, int end)
{while(begin<end){int tmp=nums[begin];nums[begin]=nums[end];nums[end]=tmp;++begin;--end;}
}void rotate(int* nums, int numsSize, int k)
{if(k>numsSize)k%=numsSize;reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums,0,numsSize-1);
}
4.空间复杂度
4.1 什么是空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
4.2 常见的空间复杂度计算举例
4.2.1 实例1:
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
分析:
相比时间复杂度来说:时间是累计的,但空间不是累计的(可以重复利用)//end、exchange、i 额外的空间
BubbleSort的空间复杂度为F(N) = (3)
使用大O渐近表示法:O(1)
4.2.2 实例2:
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;}
分析:malloc((n+1)
使用大O渐近表示法:O(N)
4.2.3 实例3:
long long Fac(size_t N)
{if(N == 1)return 1;return Fac(N-1)*N;
}
分析:Fac(N)->Fac(N-1)->.……->Fac(1)建立N个栈帧
使用大O渐近表示法:O(N)
4.2.4 实例4:
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
//VS2019->窗口->调用堆栈->双击看内存的变量
分析:栈帧销毁了可重复利用,所以递归算法的空间复杂度取决于每次调用的空间复杂度和最大递归深度:Fib(N)->Fib(N-1)->.……->Fib(1)
使用大O渐近表示法:O(N)
5.根据对空间复杂度的要求编写代码
5.1 移除元素
27. 移除元素
题述:给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,必须仅使用O(1) 额外空间并 原地 修改输入数组。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
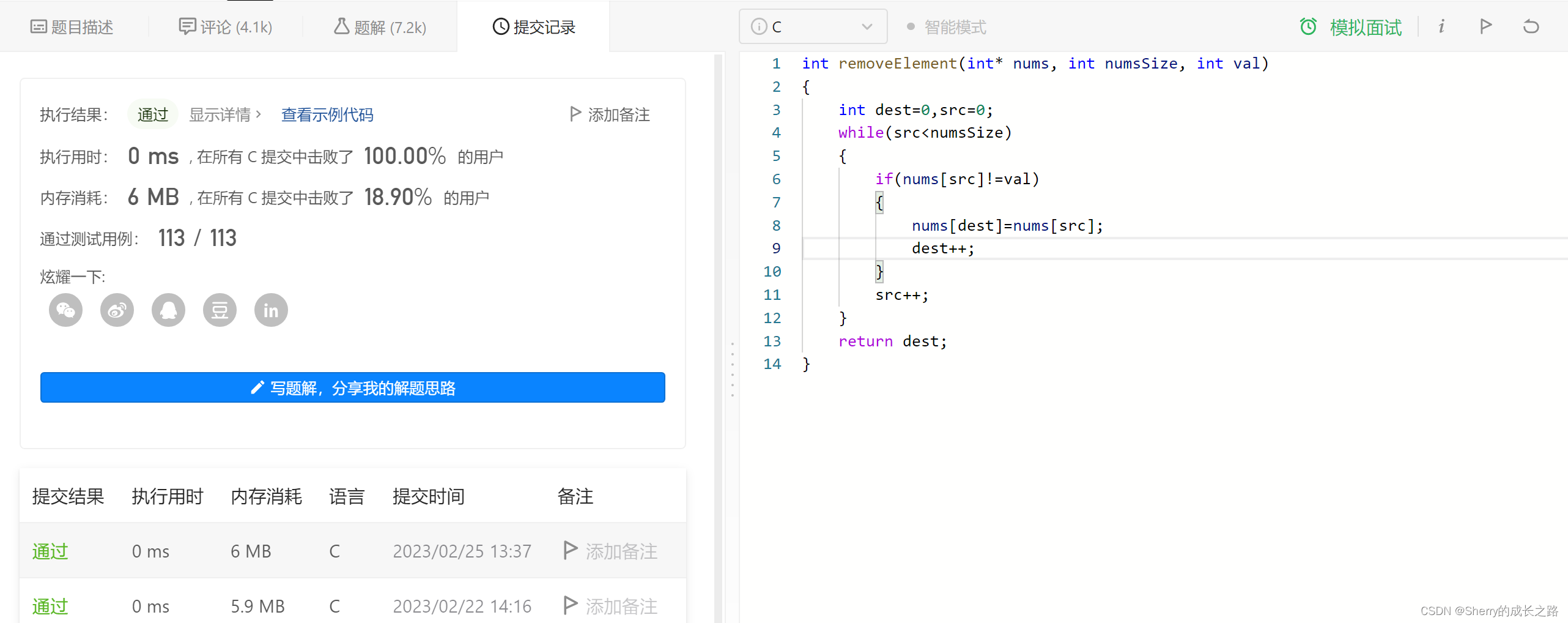
接口型:
int removeElement(int* nums, int numsSize, int val)
{int dest=0,src=0;while(src<numsSize){if(nums[src]!=val){nums[dest]=nums[src];dest++;}src++;}return dest;
}
6.总结:
今天我们认识并学习了时间复杂度和空间复杂度的相关概念,通过实例进行了分析,和一些OJ题举例。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~

相关文章:

【数据结构】时间复杂度和空间复杂度以及相关OJ题的详解分析
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1.算法效率1.1 如何衡…...

31--Vue-前端开发-Vue语法
一、前端-Vue介绍 1.前端介绍 1、HTML(5)、CSS(3)、JavaScript(ES5、ES6):编写一个个的页面 ----> 给后端(PHP、Python、Go、Java) ----> 后端嵌入模板语法 ----> 后端渲染完数据 ----> 返回数据给前端 ----> 在浏览器中查看 2、Ajax的出现 -> 后台发送异…...

这份IC设计必读书单,值得所有IC设计工程师一看!
《综合与时序分析的设计约束》 作者:Sridhar Gangadharan 本书为集成电路时序约束设计的指南,指导读者通过指定的时序要求,充分发挥IC设计的性能。本书内容包括受时序约束的关键环节的设计流程、综合时序分析、静态时序分析和布局布线等。本书…...
Acwing 蓝桥杯 第一章 递归与递推
我上周在干什么,感觉我上周啥也没训,本来两天一次的vp也没v很寄啊,再这样下去真不行了先总结一下如何爆搜:先去确定好枚举的对象枚举的对象很重要!!这直接影响了复杂度然后就是去想递归树就好了一、确定状态…...

模型部署笔记
目录模型部署工作ONNX存在的意义ONNX(Open Neural Network Exchange)ONNX示例模型推理示例Batch调整量化量化方式常见问题模型部署工作 训练好的模型在特定软硬件平台下推理针对硬件优化和加速的推理代码 训练设备平台: CPU、GPU、DSP ONN…...
多线程之wait和notify
目录 1.wait()方法 2. notify方法 因为线程之间是抢占式执行的,所以线程之间执行的先后顺序难以预知。但是实际开发中,我们希望线程之间的执行顺序是能被掌控的,比如线程2开始之前,需要线程1的某个任务先被执行。也就是说,很多时…...
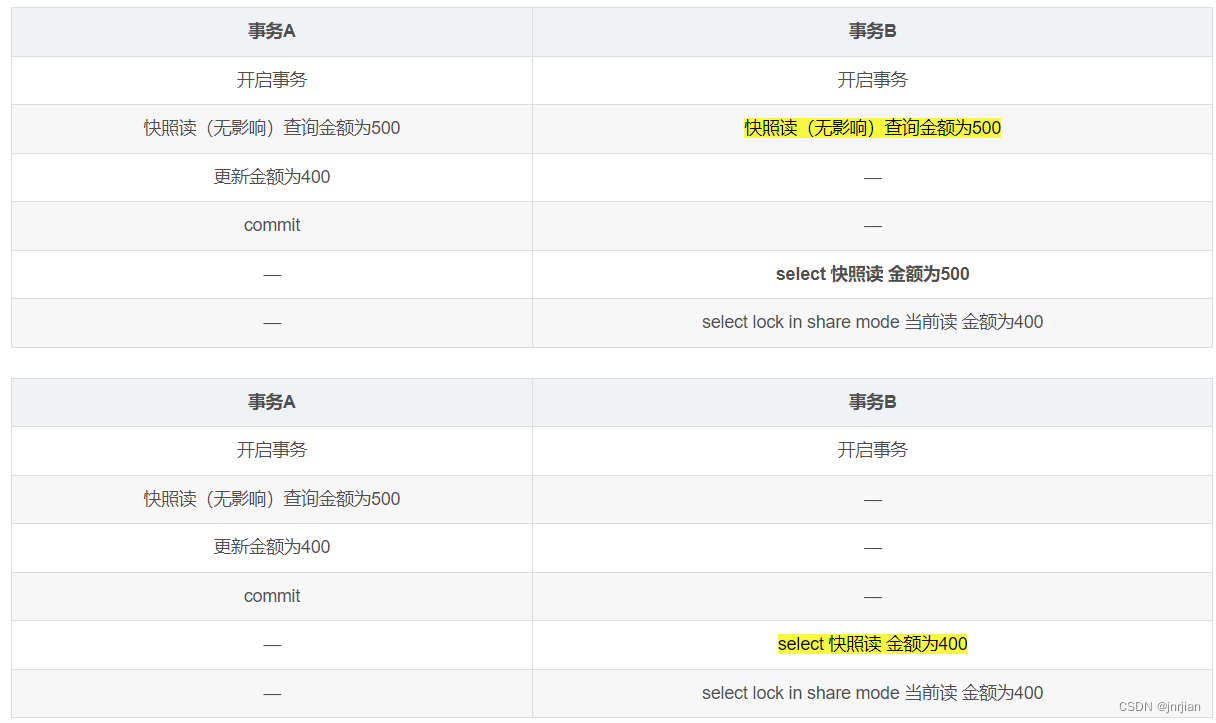
MVCC 当前读 快照读 RC read view RR下事务更新不会丢失
MVCC(multi-version-concurrent-control) MVCC是行锁的一个变种,但MVCC在很多情况下它避免了加锁。不是buffer块,而是buffer中的记录行。 MVCC (Multi-Version Concurrency Control) (注:与MVCC相对的,是基于锁的并发控制&#x…...

NCRE计算机等级考试Python真题(二)
第二套试题1、关于算法的描述,以下选项中错误的是A.算法具有可行性、确定性、有穷性的基本特征B.算法的复杂度主要包括时间复杂度和数据复杂度C.算法的基本要素包括数据对象的运算和操作及算法的控制结构D.算法是指解题方案的准确而完整的描述正确答案: …...

借助IBM Spectrum LSF为芯片行业大幅提升算力,预测未来
IBM Spectrum LSF 客户案例——上海开赟软件服务有限公司借助IBM Spectrum LSF为芯片行业大幅提升算力,预测未来 业务影响 中国芯片市场作为全球消费芯片市场重要组成部分,近年来发展迅猛。据国家统计局统计,2019年中国集成电路产量突破200…...

力扣-换座位
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:626. 换座位二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结前言 …...

DFT基本入门介绍
1.什么是DFT?2.为什么要做DFT?3.“测试”与“验证”的区别4.DFT的核心技术1)扫描路径设计(Scan Design)2)内建自测试(Bist)3)JTAG4)ATPG5.DFT工程师的岗位职责随着芯片的制程越来小(5nm), 芯片的规模越来越…...
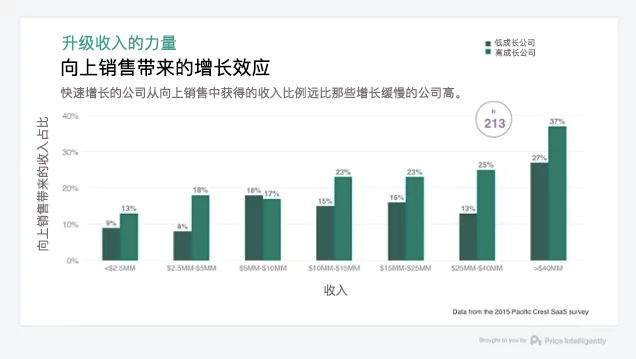
做「增长」必须懂的6大关键指标
无论你所从事的是哪个行业,增长都不是一件易事,SaaS公司想要维持长期的增长更是难上加难。这是因为SaaS公司对未来回报的依赖程度更大,反观那些传统商业模式的公司,主要的收入来源都集中在产品购买交付的时点上,而客户…...

Linux:soft lockup 检测机制
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 分析背景 本文分析基于 linux-4.14.132 内核代码分析,运行环境 Ubuntu 16.04.4 LTS QEMU ARM vexpress-a9 ,rootfs 基…...

天线理论知识4——非频变天线
目录 简介自补结构巴比涅原理天线的描述常见的非频变天线简介 所谓的非频变天线指的是天线的参数几乎不随着频率的改变而发生变化。 自补结构 天线的自补结构指的是:由无限大且无厚度的理想导电区域的自由空间中的非导电区域放置一起的结构称为自补结构。包含金属部分和非金…...

基础架构组件选型及服务化
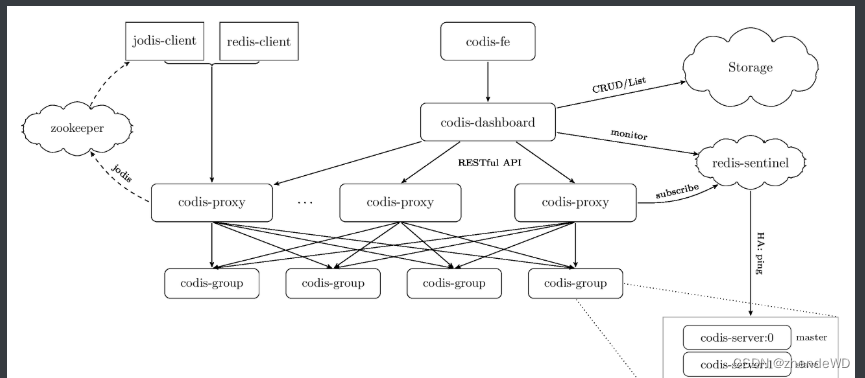
常见的分布式基础架构组件 分布式服务化框架,业界开源产品比如 Dubbo、Spring Cloud 这样的框架;分布式缓存及框架,业界如 Redis、Memcached,框架如 Codis 和 Redis Cluster;数据库及分布式数据库框架,这两…...
leetcode-每日一题-1247(中等,数学逻辑)
这道题当理解清了意思之后,只要是s1和s2的某位置的字母一样时我们就可以忽视比如s1"xxxxxxyyyy"; 就可以看成s1"xxxyyyy";s2"xxxyyyxxxx"; s2"yyyxxxx";其次就是只有当x和y位置差异产生的数量同奇偶的时候才可以构成相等字…...
前端面试题 —— 计算机网络(一)
目录 一、常见的HTTP请求头和响应头 二、HTTP状态码304是多好还是少好? 三、OPTIONS请求方法及使用场景 四、对keep-alive的理解 五、HTTP协议的优点和缺点 六、URL有哪些组成部分? 七、HTTPS通信(握手)过程 八、HTTPS的特…...
分布式-分布式缓存笔记
分布式系统缓存 缓存分类 前端缓存 前端缓存包括页面和浏览器缓存,如果是 App,那么在 App 端也会有缓存。当你打开商品详情页,除了首次打开以外,后面重复刷新时,页面上加载的信息来自多种缓存。 页面缓存属于客户端…...

【反序列化漏洞-01】为什么要序列化
为什么要序列化百度百科上关于序列化的定义是,将对象的状态信息转换为可以存储或传输的形式(字符串)的过程。在序列化期间,对象将其当前状态写入到临时或持久性存储区(非关系型键值对形式的数据库Redis,与数组类似)。以后,可以通过…...

用c语言模拟实现常用字符串函数
目录 一.常用字符串函数介绍 1.strlen 2. strcpy 3.strcmp 4.strcat 5.strstr 二.模拟实现常用字符串函数 1.strlen 2.strcpy 3.strcmp 4.strcat 5.strstr 一.常用字符串函数介绍 1.strlen 字符串strlen是用来求字符串长度的,我们可以打开cpp网站查看有关…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
