强化学习RL 01~ 数学基础
目录
RL理解要点
1. RL数学基础
1.1 Random Variable 随机变量
1.2 概率密度函数 Probability Density Function(PDF)
1.3 期望 Expectation
1.4 随机抽样 Random Sampling
2. RL术语 Terminologies
2.1 agent、state 和 action
2.2 策略 policy π
2.3 奖励 reward
2.4 状态转移 state transition
2.5 agent environment interaction 环境交互
2.6 强化学习中的随机性 Randomness in Reinforcement Learning
2.7 play the game using AI
2.8 rewards、returns
2.8.1 Discounted return Ut 折扣回报
2.8.2 Random in Returns
2.9 value function 价值函数
2.9.1 Action-value function Qπ(s, a)
2.9.2 Optimal action-value function Q*
2.9.3 State-value function Vπ
3. How does AI control the agent?
3.1 policy function π
3.2 Q*(s, a)函数
3.3 Open AI gym
参考
RL理解要点
- RL学什么呢?就是要学习policy策略函数
1. RL数学基础
1.1 Random Variable 随机变量
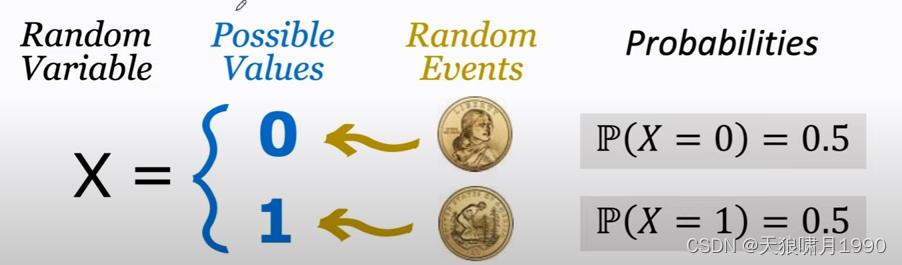
Random Variable: a variable whose values depend on outcomes of a random event. 随机变量是一个未知的量,它的值取决于随机事件的结果。
用大写字母表示随机变量 random variable,用小写字母表示随机变量观测值 observed value。
1.2 概率密度函数 Probability Density Function(PDF)
本质:就是一个概率分布(0.2, 0.3, 0.5)。
PDF provides a relative likelihood that the value of the random variable would equal that sample.
e.g. Gaussian distribution
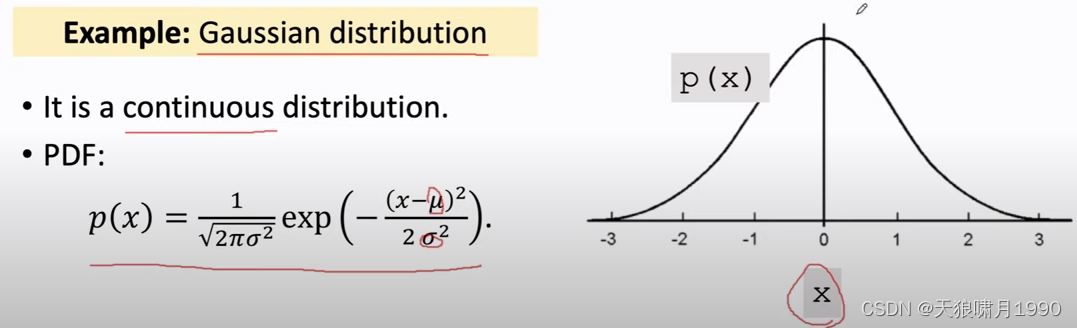
连续分布、离散分布。用表示其定义域domain

1.3 期望 Expectation
本质:是平均值,是预估结果。

1.4 随机抽样 Random Sampling

2. RL术语 Terminologies
2.1 agent、state 和 action
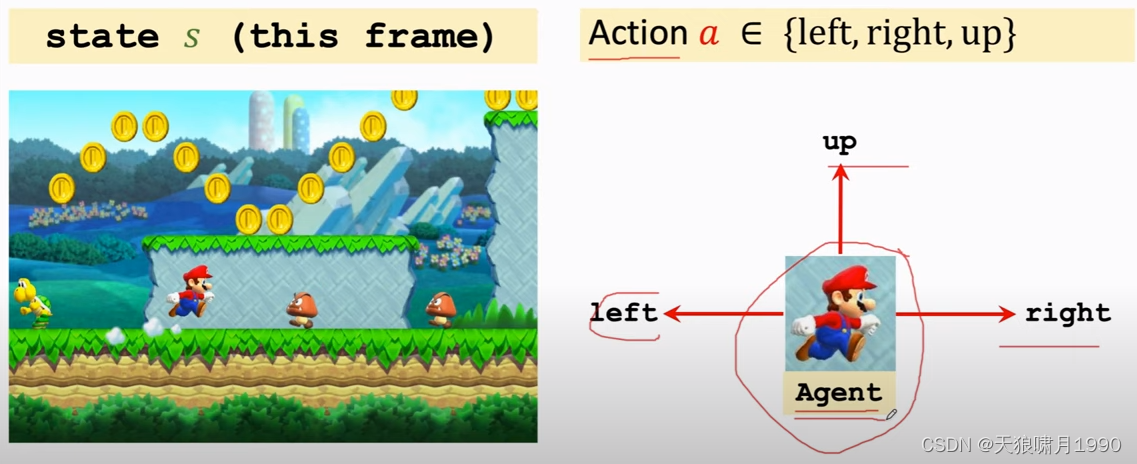
- 可以近似理解当前图片frame就是state
- agent,翻译为“智能体”
- 当前state,agent可以做的动作叫action,包括{'left', 'right', 'up'}
2.2 策略 policy π
本质:policy策略是一个概率密度函数,就是根据state生成一个动作action概率分布。
policy根绝观测到状态state,做出决策,然后控制agent运动。
Note that policy函数是随机的。

2.3 奖励 reward
agent做出一个动作,游戏就会给出一个奖励reward
奖励定义的好坏,非常影响强化学习的结果。

2.4 状态转移 state transition
agent做出一个动作,游戏就会给出一个新的状态state,这个过程就叫state transition。
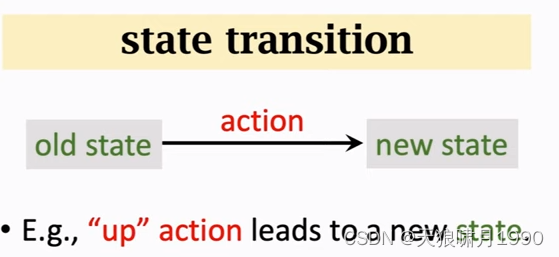
- state transition can be random.
- randomness is from the environment. 状态转移的随机性是从环境中来的,这里的环境是游戏的程序。
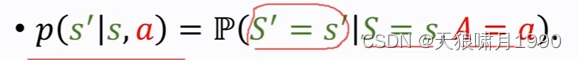
可以把状态转移用p函数来表示,这是个条件概率密度函数,意思是如果观测到当前状态s和动作a ,p函数就表示s prime的概率。
2.5 agent environment interaction 环境交互

agent和environment,agent看到状态st之后,要做出一个动作at,agent做出动作at后,环境environment会更新状态、把状态变成st+1,同时environment还会给agent一个奖励rt。
2.6 强化学习中的随机性 Randomness in Reinforcement Learning
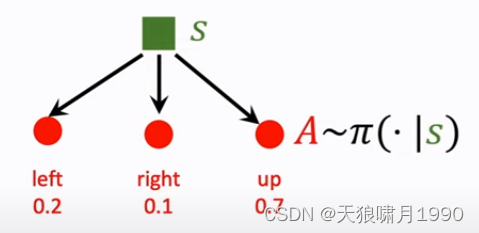
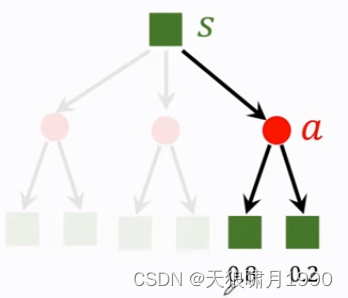
- Actions have randomness. actions是根据policy函数随机抽样得到的,我们用policy函数来控制agent,给定当前状态s,agent输出的动作a是根据策略函数policy输出的概率分布来随机抽样。
- state transitions have randomness. 假定agent做出了up action,环境environment就要生成下一个状态s',这个状态s'具有随机性,environment用状态概率转移函数p算出概率,然后用概率来随机抽样得到下一个状态s',
2.7 play the game using AI
通过强化学习学出policy function π,AI就是用policy函数来控制agent。

游戏当前状态s1,AI用policy函数来算一个概率,然后随机抽样得到动作a1,然后环境会生成下一个状态s2,并且给agent一个奖励r1,然后环境会拿新的状态s2作为输入,并用policy function来算概率,然后随机抽样得到新的动作a2,然后这样一直循环下去,直到打赢游戏或game over。
得到一个轨迹(state, action, reward)trajectory:s1,a1,r1,s2,a2,r2,...,st,at,rt。
2.8 rewards、returns
Return翻译为“回报”,也称作cumulative future reward,“未来的累积奖励”。
把t时刻的return记作Ut,就是把从t时刻开始的reward全都加起来,一直加到游戏结束时的最后一个奖励。
Question: Are Rt and Rt+1 equally important?
Future reward is less valuable than present reward.
Rt+1 should be given less weight than Rt. --> Discounted return
2.8.1 Discounted return Ut 折扣回报
γ,折扣率 discount rate gamma(tuning hyper-parameter),介于[0, 1]。

折扣率是个超参数,需要我们自己来调,折扣率的设置对强化学习的效果有一定的影响。
2.8.2 Random in Returns
Return Ut的随机性。假如游戏已经结束了,所有的奖励已经观测到了,那么奖励是数值,用rt表示;如果在t时刻游戏还没结束,那么奖励还是随机变量,还没被观测到,用Rt表示。

随机性有两个来源:一是action a是从policy概率分布中随机抽样得到的;二是下一状态new state,状态转移函数p输出一个概率分布,environment从中随机抽样得到一个新的状态s'。
- For any i ≥ t, the reward Ri depends on Si and Ai. 当前agent处在的状态s和做出的动作a,就决定了奖励Ri是什么。
- 回报Ut是Rt、Rt+1等等的加权求和,而Ri是由Si和Ai决定的,所以给定st,Ut跟t时刻开始所有的动作At,At+1,At+2,..和状态St+1,St+2,...都有关了。
2.9 value function 价值函数
2.9.1 Action-value function Qπ(s, a)

在t时刻,你并不知道Ut是什么。Ut是个随机变量,它依赖于未来所有的动作At,At+1,At+2,...和未来所有的状态St,St+1,St+2,...
Ut未知,那我该怎么评估当前的形势呢?
对Ut求期望,把里面的随机性都用积分积掉,得到一个实数。
把Ut当作未来所有动作Ai和所有状态Si的一个函数,未来的动作和状态都有随机性,动作Ai的概率密度函数是policy function π,状态Si的概率密度函数是状态转移函数p,期望就是针对未来Si和Ai求得,出了St和At,其余的随机变量都是积分积掉,被积掉的是At+1,At+2等动作、St+1,St+2等动作,求期望得到的动作价值函数Qπ,其只跟当前动作at、状态st有关。
函数Qπ还与policy function π有关,因为积分时会用到policy函数,π函数不一样,Qπ就会不一样。
Qπ的直观意义:如果用状态价值函数Qπ,那么在当前状态st下做动作at是好还是坏。
已知policy函数π,那么Qπ就会给当前状态下所有动作A打分,然后就知道哪个动作好、哪个动作不好。
2.9.2 Optimal action-value function Q*
如何把action-value function中的π去掉呢?
可以对Qπ关于π求最大化。意思是我们有无数种policy函数π,但我们应该使用最好的那一种!
最好的policy函数就是让Qπ最大化的那个π,得到函数Q*称为optimal action-value function。

Q*跟π无关,它的直观意义:Q*可以用来对当前动作at做评价--分数,比如下围棋是,你把棋子放在这个位置胜算有多大,你把棋子放在那个位置胜算有多大。
Q*非常有用,agent可以根据Q*对actions的评价来做决策。
2.9.3 State-value function Vπ

状态价值函数Vπ,它是action-value function动作价值函数Qπ的期望。
Qπ与状态st、动作A有关,可以把A当作随机变量,求期望把它消掉,这样Vπ只跟st和π有关。
Vπ直观意义:Vπ可以告诉我们当前局势好不好,比如下围棋,Vπ可以告诉我们当前胜算有多大,是快赢了还是快输了。
![]()
这里的期望是根据A求得,A的概率密度函数是policy function π。根据期望定义,可以把期望写成连加或积分的形式。
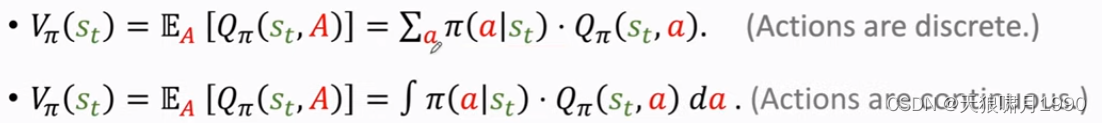
For fixed policy π, Vπ(s) evaluates how good the situation is in state s.
Es[Vπ(S)] evaluates how good the policy π is.
3. How does AI control the agent?
3.1 policy function π
一种方法是学一个策略函数policy π
有了policy 函数π,就可以用来控制agent来做动作。

3.2 Q*(s, a)函数
另一种方法是学习optimal action-value function Q*(s, a)函数,它是value based model
假如有了Q*函数,agent可以根据Q*函数来做动作了。
如果处在状态s,那么做动作a是好还是坏。没观测到一个状态st,就把st作为Q*函数的输入,让Q*函数对每一个函数做一个评价,假如up move的q值最大,因为q值是对未来奖励reward总和的期望,所以选up获取以期在未来获得更多奖励。

3.3 Open AI gym
- 经典控制问题
- atari game
- 连续控制问题 continuous control tasks


参考
1. 王树森~强化学习 Reinforcement Learning
2. https://www.cnblogs.com/pinard/category/1254674.html
相关文章:

强化学习RL 01~ 数学基础
目录 RL理解要点 1. RL数学基础 1.1 Random Variable 随机变量 1.2 概率密度函数 Probability Density Function(PDF) 1.3 期望 Expectation 1.4 随机抽样 Random Sampling 2. RL术语 Terminologies 2.1 agent、state 和 action 2.2 策略 policy π 2.3 奖励 reward …...
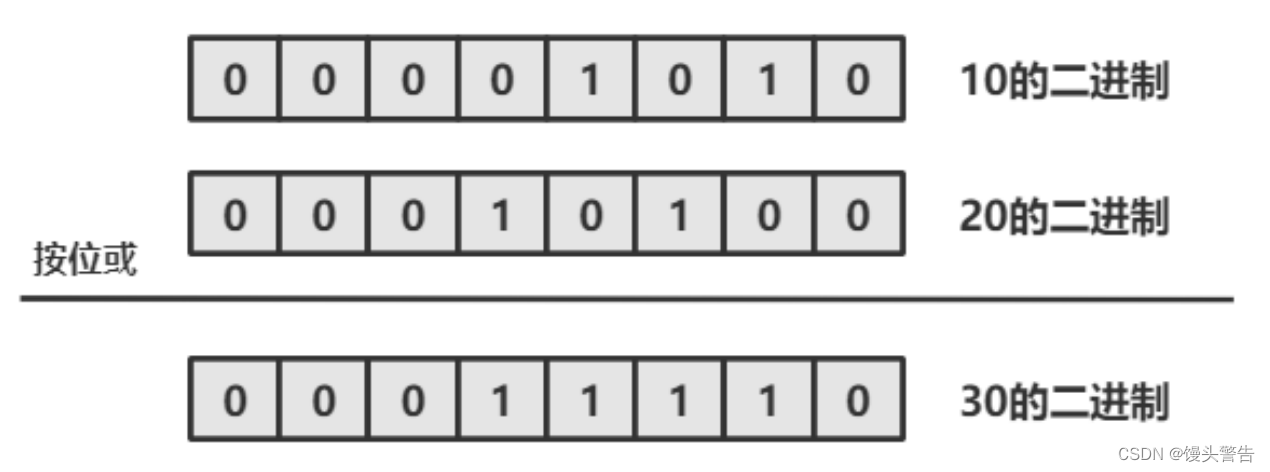
Java的运算符
目录 一、什么是运算符 二、算术运算符 1. 基本四则运算符:加减乘除模( - * / %) 2、增量运算符 - * % 3. 自增/自减运算符 -- 三、关系运算符 四、 逻辑运算符(重点) 1. 逻辑与 && 2. 逻辑或 || 3. 逻辑非 ! 4. 短路求值…...

扫地机器人(蓝桥杯C/C++)
题目描述 小明公司的办公区有一条长长的走廊,由 NN 个方格区域组成,如下图所示。 走廊内部署了 KK 台扫地机器人,其中第 ii 台在第 A_iAi 个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干净。…...
如何理解API?API 是如何工作的?(5分钟诠释)
大家可能最近经常听到 API 这个概念,那什么是API,它又有什么特点和好处呢? wiki 百科镇楼 …[APIs are] a set of subroutine definitions, protocols, and tools for building application software. In general terms, it’s a set of cle…...

PAT--1111 对称日
央视新闻发了一条微博,指出 2020 年有个罕见的“对称日”,即 2020 年 2 月 2 日,按照 年年年年月月日日 格式组成的字符串 20200202 是完全对称的。 给定任意一个日期,本题就请你写程序判断一下,这是不是一个对称日&a…...

前端纯函数和副作用概念,且在react上的体现详解
什么是纯函数 纯函数是这样一种函数,即相同的输入,永远会得到相同的输出的函数,而且没有任何可观察的副作用。 什么是副作用 副作用是在计算结果的过程中,系统状态的一种变化,或者与外部世界进行的可观察的交互。 个…...

转行软件测试3年了,听前辈说测试前途是IT里最low的,我慌了......
互联网行业的技术岗位一般分为研发、测试和运维,虽然前些年测试一直都不如研发岗位那么吃香。但现在随着国内对软件测试的重视,我国互联网企业对软件测试的需求在未来还将继续增大。听起来软件测试的就业形势一片大好,那么到底软件测试的发展…...
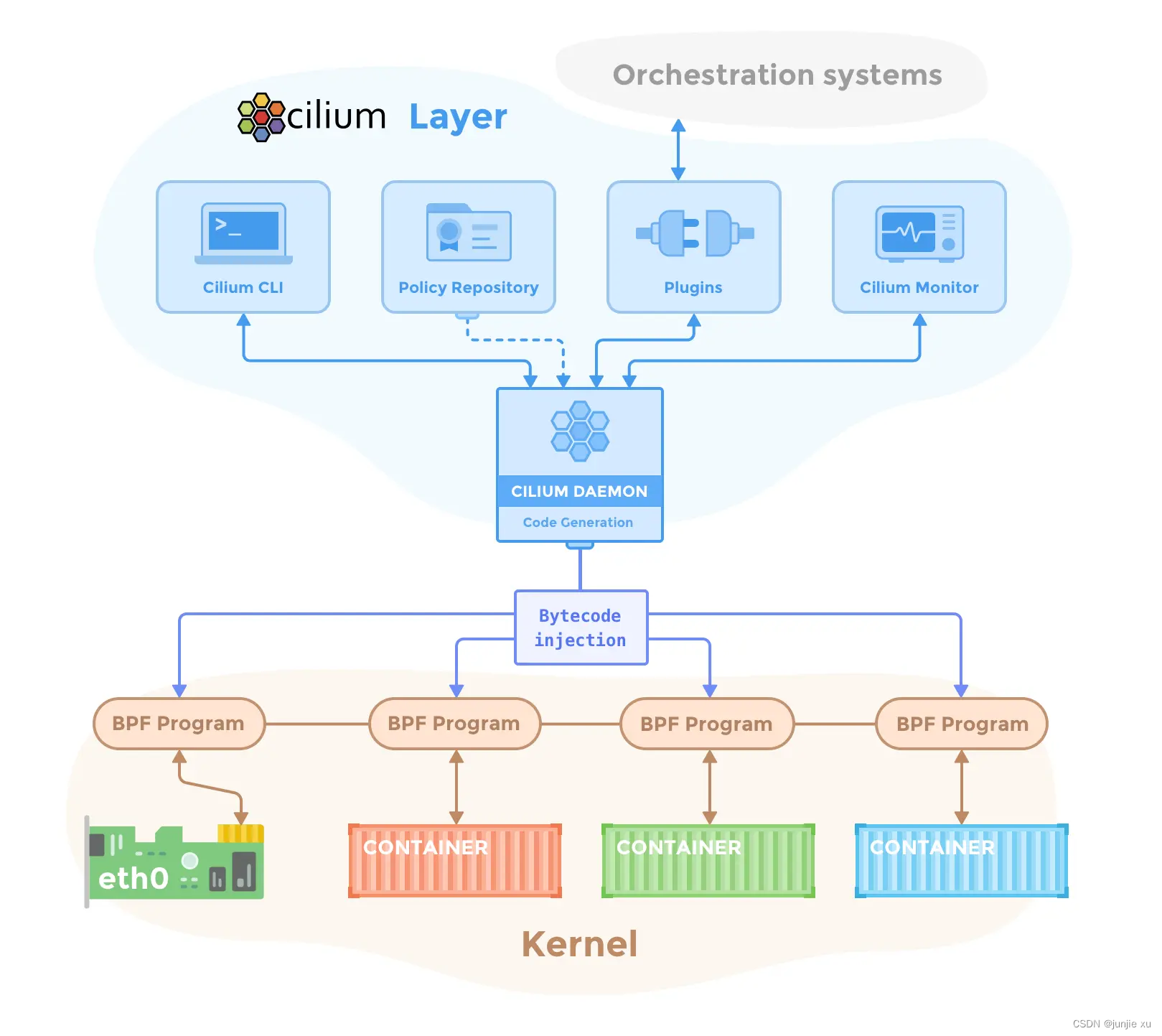
CNI 网络流量 5.1 Cilium 介绍和原理
文章目录简介安装组件和原理Cilium-agent初始化IPAMCNICilium cli 的使用bpfMap 的操作Cilium-agentEbpf简介 Cilium 是一个用于容器网络领域的开源项目,主要是面向容器而使用,用于提供并透明地保护应用程序工作负载(如应用程序容器或进程&a…...
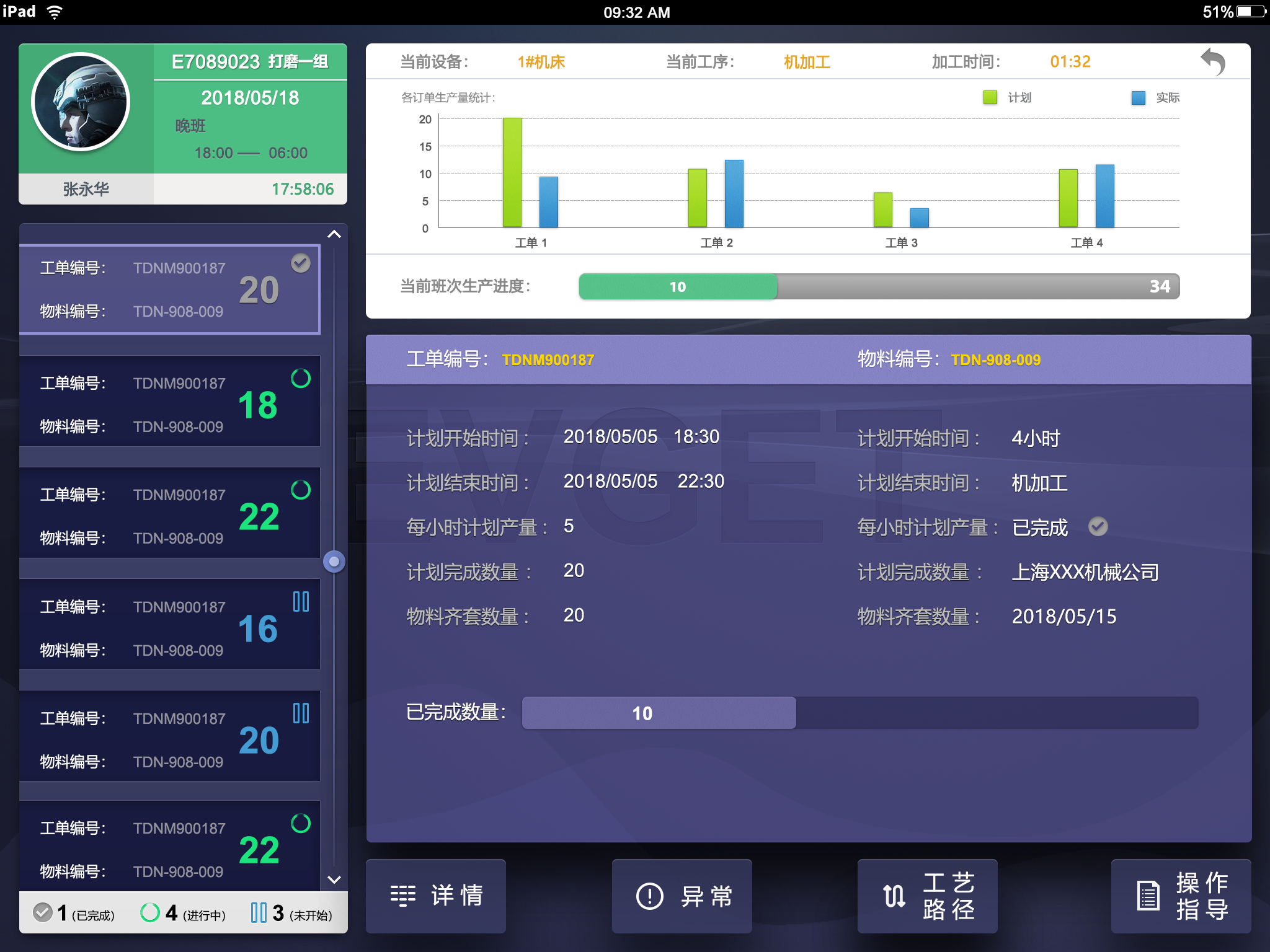
机加行业MES解决方案,助力企业打造数字化透明车间
机械加工行业的主要原材料占整个生产物料成本的95%~99%,以挖掘机为例,原材料有各种规格的钢板、焊丝、焊条、油漆以及各种气体等,其中主要原材料是钢板,占原材料比率的98%以上。 因此机械加工mes的原材料管理是机械加工行业信息化…...
C/C++每日一练(20230227)
目录 1. 按要求排序数组 ★ 2. Z 字形变换 ★★ 3. 下一个排列 ★★ 1. 按要求排序数组 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中,数字 1 的数目升序排序。 如果存在多个数字二进制中 1 的数目相同,则必须将它们按照数值大小…...

总结SpringBoot1.x迁移到2.x需要注意的问题
SpringBoot1.x和SpringBoot2.x版本差异化还是比较大的,有些三方依赖组件有些是基于2.0版本为标准升级的,当我们将项目由1.0升级到2.0时会出现依赖的方法不存在或方法错误,需要逐个去调整,下面总结了我们升级实践过程中遇到的一些问…...

Api接口小知识
应用程序接口API(Application Programming Interface),是提供特定业务输出能力、连接不同系统的一种约定。这里包括外部系统与提供服务的系统(中控系统)或者后台不同的系统之间的交互点。包括外部接口、内部接口、内部接口有包括&…...

「JVM 高效并发」Java 协程
Java 语言抽象和隐藏了各种操作系统线程差异性的接口,这曾经是它区别于其他编程语言的一大优势,但在某些场景下,却已经出现了疲态; 文章目录1. 内核线程的局限2. 协程的复苏3. Java 的解决方案1. 内核线程的局限 在微服务架构中&…...

Web Spider案例 网洛者 第一题 JS混淆加密 - 反hook操作 练习(五)
文章目录一、资源推荐二、第一题 JS混淆加密 - 反hook操作2.1 过控制台反调试(debugger)2.2 开始逆向分析三、python具体实现代码四、记录一下,execjs调用混淆JS报错的问题总结提示:以下是本篇文章正文内容,下面案例可供参考 一、资源推荐 …...
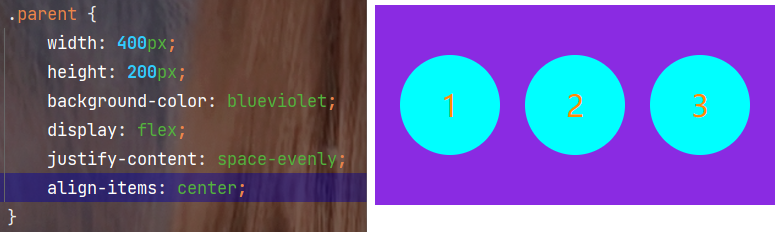
前端基础之CSS扫盲
文章目录一. CSS基本规范1. 基本语法格式2. 在HTML引入CSS3. 选择器分类二. CSS常用属性1. 文本属性2. 文本格式3. 背景属性4. 圆角矩形和圆5. 元素的显示模式6. CSS盒子模型7. 弹性布局光使用HTML来写一个前端页面的话其实只是写了一个大体的框架, 整体的页面并不工整美观, 而…...

mysql组复制、mysql路由器、mysql的MHA高可用
文章目录前言一、mysql组复制1.实验机配置2.测试二、mysql路由器三、mysql之MHA高可用1.MHA概念1.创建一主两从集群2.MHA部署3.故障切换前言 一、mysql组复制 1.实验机配置 server1配置 首先停止数据库 [rootserver1 mysql]# /etc/init.d/mysqld stop Shutting down MySQL..…...

一篇搞懂springboot多数据源
好文推荐 https://zhuanlan.zhihu.com/p/563949762 mybatis 配置多数据源 参考文章 https://blog.csdn.net/qq_38353700/article/details/118583828 使用mybatis配置多数据源我接触过的有两种方式,一种是通过java config的方式手动配置两个数据源,…...
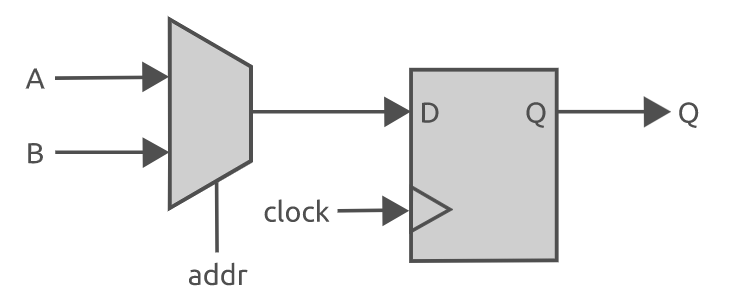
Verilog 数据类型和数组简介
在这篇文章将讨论 verilog 中最常用的数据类型,包括对数据表示,线网类型、变量类型,向量类型和数组的讨论。尽管 verilog 被认为是一种弱类型语言(loosely typed),但设计者仍必须在 Verilog 设计中为每个端…...

【数据结构】时间复杂度和空间复杂度以及相关OJ题的详解分析
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录1.算法效率1.1 如何衡…...

31--Vue-前端开发-Vue语法
一、前端-Vue介绍 1.前端介绍 1、HTML(5)、CSS(3)、JavaScript(ES5、ES6):编写一个个的页面 ----> 给后端(PHP、Python、Go、Java) ----> 后端嵌入模板语法 ----> 后端渲染完数据 ----> 返回数据给前端 ----> 在浏览器中查看 2、Ajax的出现 -> 后台发送异…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
