HMM(隐马尔科夫模型)-理论补充2
目录
一.大数定理
二.监督学习方法
1.初始概率
2.转移概率
3.观测概率
三.Baum-Welch算法
1.EM算法整体框架
2. Baum-Welch算法
3.EM过程
4.极大化
5.初始状态概率
6.转移概率和观测概率
四.预测算法
1.预测的近似算法
2.Viterbi算法
1.定义
2. 递推:
3. 终止:
五.总结
一.大数定理
假设已给定训练数据包含S个长度相同的观测序列和对应的状态序列{(O1,I1),(O2,I2)…(Os,Is)},那么,可以直接利用Bernoulli大数定理的结论“频率的极限是概率”,给出HMM的参数估计。
二.监督学习方法
1.初始概率
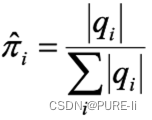
2.转移概率
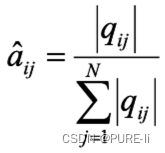
3.观测概率

三.Baum-Welch算法
若训练数据只有观测序列,则HMM的学习需要使用EM算法,是非监督学习。
1.EM算法整体框架
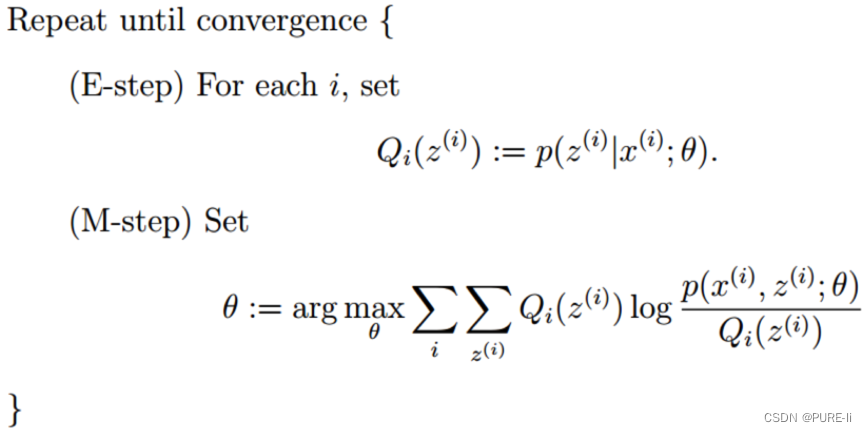
2. Baum-Welch算法
所有观测数据写成O=(o1,o2…oT),所有隐数据写成I=(i1,i2…iT),完全数据是(O,I)=(o1,o2…oT,i1,i2…iT),完全数据的对数似然函数是lnP(O,I|λ)
假设 是HMM参数的当前估计值,λ为待求的参数。
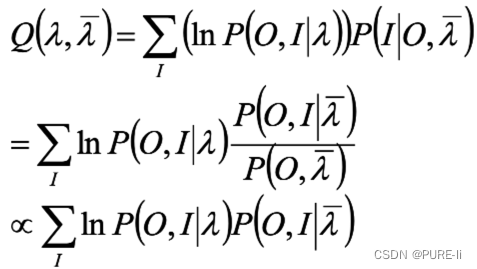
3.EM过程
根据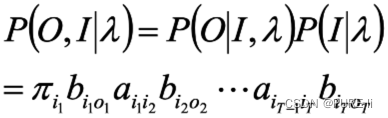
函数可写成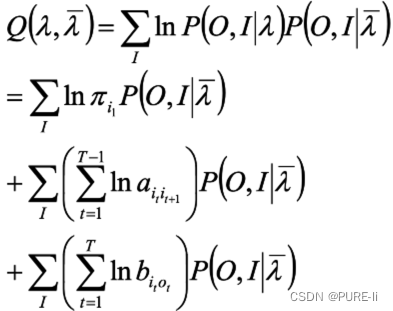
4.极大化
极大化Q,求得参数A,B,π
由于该三个参数分别位于三个项中,可分别极大化
![]()
注意到πi满足加和为1,利用拉格朗日乘子法,得到:
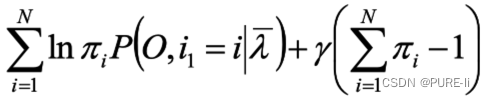
5.初始状态概率
对上式相对于πi求偏导,得到:
![]()
对i求和,得到:
![]()
从而得到初始状态概率:
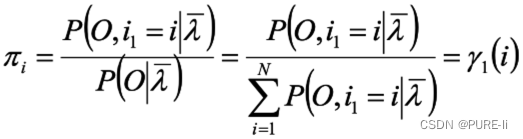
6.转移概率和观测概率
第二项可写成:
![]()
仍然使用拉格朗日乘子法,得到
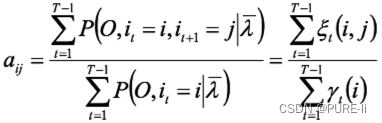
同理,得到:
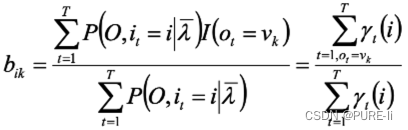
四.预测算法
1.预测的近似算法
在每个时刻t选择在该时刻最有可能出现的状态it*,从而得到一个状态序列I*={i1*,i2*…iT*},将它作为预测的结果。
给定模型和观测序列,时刻t处于状态qi的概率为:
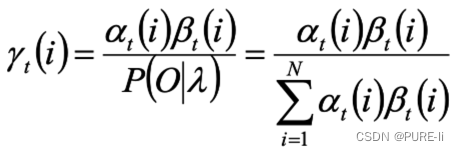
选择概率最大的i作为最有可能的状态
会出现此状态在实际中可能不会发生的情况
算法:走棋盘/格子取数
给定m*n的矩阵,每个位置是一个非负整数,从左上角开始,每次只能朝右和下走,走到
右下角,求总和最小的路径。

走的方向决定了同一个格子不会经过两次。
若当前位于(x,y)处,它来自于哪些格子呢?
dp[0,0]=a[0,0] / 第一行(列)累积
dp[x,y] = min(dp[x-1,y]+a[x,y],dp[x,y-1]+a[x,y])
即:dp[x,y] = min(dp[x-1,y],dp[x,y-1]) +a[x,y]
2.Viterbi算法
Viterbi算法实际是用动态规划解HMM预测问题,用DP求概率最大的路径(最优路径),这是一条路径对应一个状态序列。
定义变量δt(i):在时刻t状态为i的所有路径中,概率的最大值。
1.定义
![]()
2. 递推:
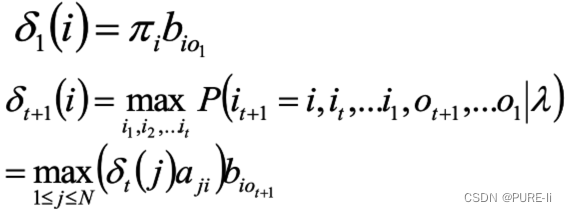
3. 终止:
![]()
五.总结
马尔科夫模型可以用来统一解释贪心法和动态规划。
HMM解决标注问题,在语音识别、NLP、生物信息、模式识别等领域被广泛使用。
定义变量δt(i):在时刻t状态为i的所有路径中,概率的最大值。
加强算法模型和实践问题的相互转换能力。
相关文章:
HMM(隐马尔科夫模型)-理论补充2
目录 一.大数定理 二.监督学习方法 1.初始概率 2.转移概率 3.观测概率 三.Baum-Welch算法 1.EM算法整体框架 2. Baum-Welch算法 3.EM过程 4.极大化 5.初始状态概率 6.转移概率和观测概率 四.预测算法 1.预测的近似算法 2.Viterbi算法 1.定义 2. 递推࿱…...
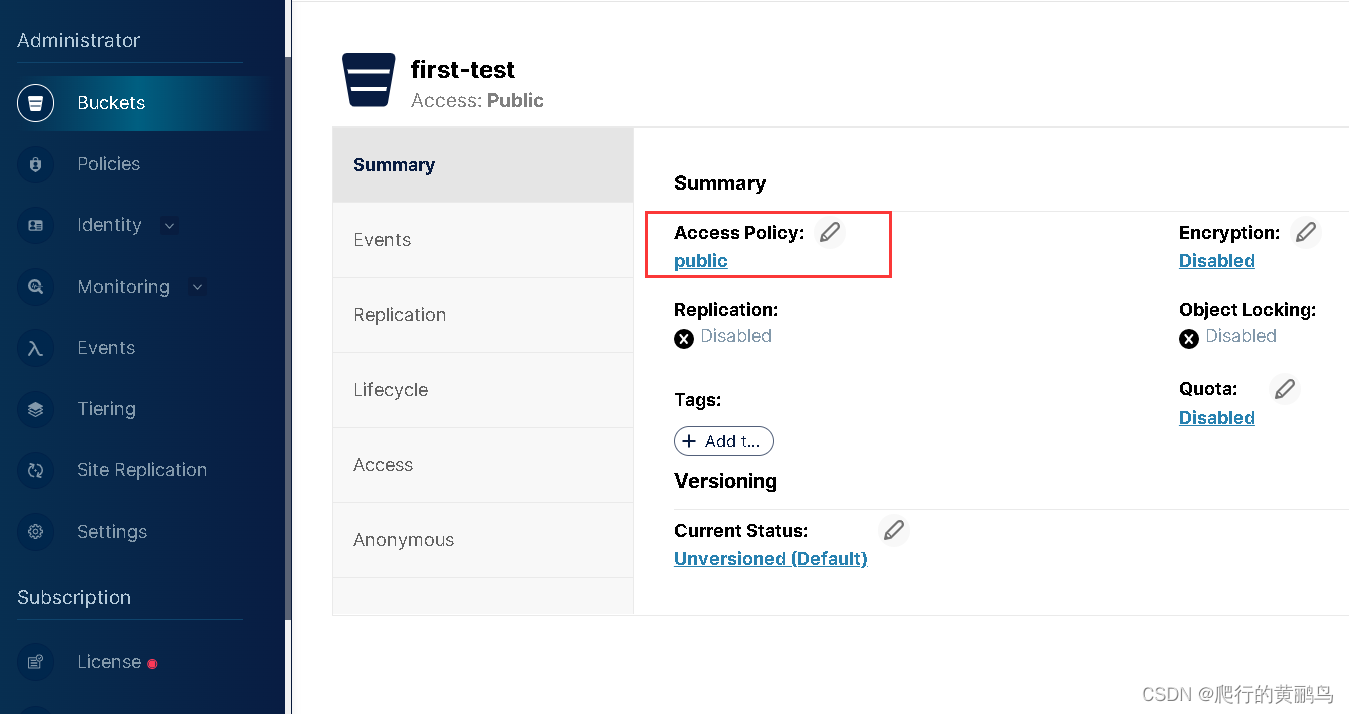
【分布式系统】MinIO之Multi-Node Multi-Drive架构分析
文章目录架构分析节点资源硬盘资源服务安装安装步骤创建系统服务新建用户和用户组创建环境变量启动服务负载均衡代码集成注意最近打算使用MinIO替代原来使用的FastDFS,所以一直在学习MinIO的知识。这篇文章是基于MinIO多节点多驱动的部署进行研究。 架构分析 节点资…...
【无标题】(2019)NOC编程猫创新编程复赛小学组真题含参考
(2019)NOC编程猫创新编程复赛小学组最后6道大题。前10道是选择填空题 略。 这道题是绘图题,没什么难度,大家绘制这2个正十边形要注意:一是不要超出舞台;二是这2个正十边形不要相交。 这里就不给出具体程序了…...
【尚硅谷MySQL入门到高级-宋红康】数据库概述
1、为什么要使用数据库 数据的持久化 2、数据库与数据库管理系统 2.1 数据库的相关概念 2.2 数据库与数据库管理系统的关系 3、 MySQL介绍 MySQL从5.7版本直接跳跃发布了8.0版本 ,可见这是一个令人兴奋的里程碑版本。MySQL 8版本在功能上做了显著的改进与增强&a…...
SpringBoot集成Redis并实现数据缓存
应用场景 存放Token、存放用户信息或字典等需要频繁访问数据库获取但不希望频繁访问增加数据库压力且变化不频繁的数据。 集成步骤 1. 新建 Maven 项目并引入 redis 依赖【部分框架有可能已经集成,会导致依赖文件有差异】 <dependency><groupId>org…...
SpringBoot配置文件(properties yml)
查看官网更多系统配置项:https://docs.spring.io/spring-boot/docs/current/reference/html/application-properties.html#application-properties 1.配置⽂件作⽤ 整个项⽬中所有重要的数据都是在配置⽂件中配置的,⽐如:数据库的连接信息&am…...

css 画图之质感盒子
前言 css 众所周知可以做很多的事情,比如:界面效果、特效、独特的样式等。今天给各位朋友带来的是以box-shadow来画一个很有质感效果的一个盒子。 之前在网上冲浪的时候,发现了这样的一个效果,所以来记录一下。 下面是实现后的…...

面了一个月,终于让我总结出了这份最详细的接口测试面试题
目录 1、你们公司是如何做接口测试的? 2、什么时候开展接⼝测试? 3、接⼝测试和UI测试的工作是否重复? 4、接口测试框架怎么搭建? 5、接⼝之间有依赖时怎么处理? 6、如何判断接⼝测试的结果(成功或失败&a…...

{新}【java开发环境安装】完整工作环境安装配置
公司新发了一台红米笔记本,打算用新的笔记本,开启自己新的工作旅程,其中把做个的事都记录一边,以便实现,听、读、视频图像、讨论、实践、教人的一个学习过程。 一、Java开发环境安装 找到安装包下载;在官…...

Python|每日一练|数组|数学|图算法|字符串|动态规划|单选记录:加一|迷宫问题|扰乱字符串
1、加一(数组,数学) 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以…...

MySQL 使用IF判断
mysql判断语句 1、IF 和IFNULL IF(表达式1,表达式2,表达式3); 含义:如果表达式1为true,则返回表达式2的值,否则返回表达式3的值,表达式的值类型可以为数字或字符串 例:判断对错 SELECT IF(TRUE…...
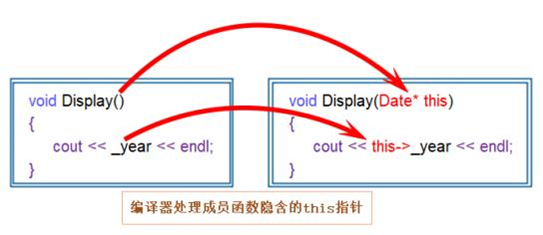
C++类与对象(上)【详析】
目录1.面向过程和面向对象初步认识2.类的引入3.类的定义4.类的访问限定符及封装4.1访问限定符4.2封装5.类的作用域6.类的实例化7.类对象模型7.1 如何计算类对象的大小8.this关键字如果说我们对C的初步认识,是觉得C是对C语言不足之处的进行修补,在认识完类…...
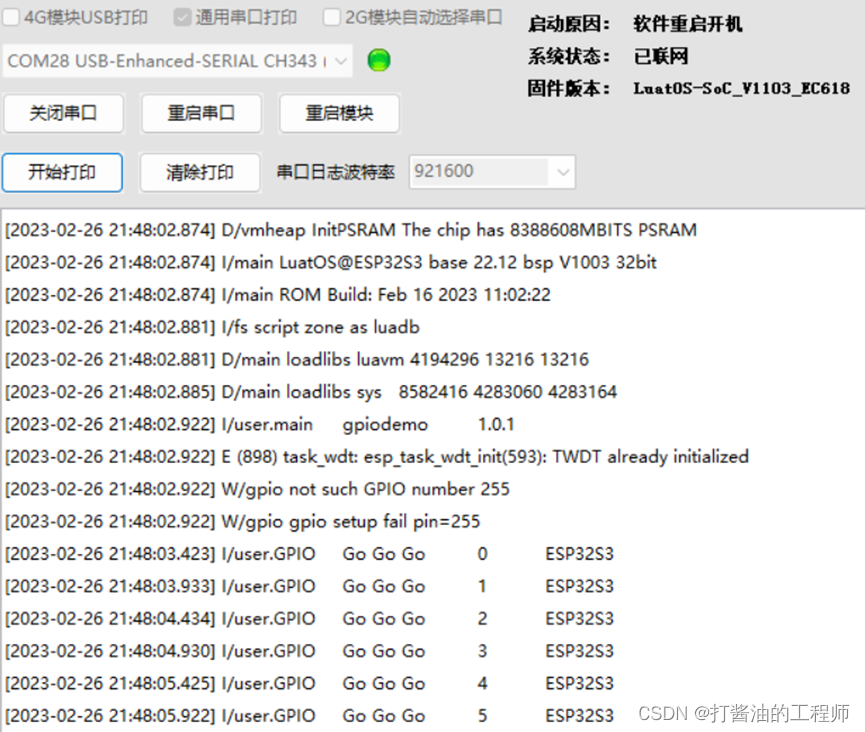
AIR系列|板载LED|gpio引脚选择|GPIO|流水灯|LuatOS-SOC接口|官方demo|学习(20-1):GPIO库基础
AIR系列各型号开发板板载LED对应管脚及GPIO控制代码 AIR103: rtos_bsp "AIR103" then -- Air103开发板LED引脚编号--return pin.PB26, pin.PB25, pin.PB24return 42,41,40 AIR105: rtos_bsp "AIR105" then -- Air105开发板LED引…...
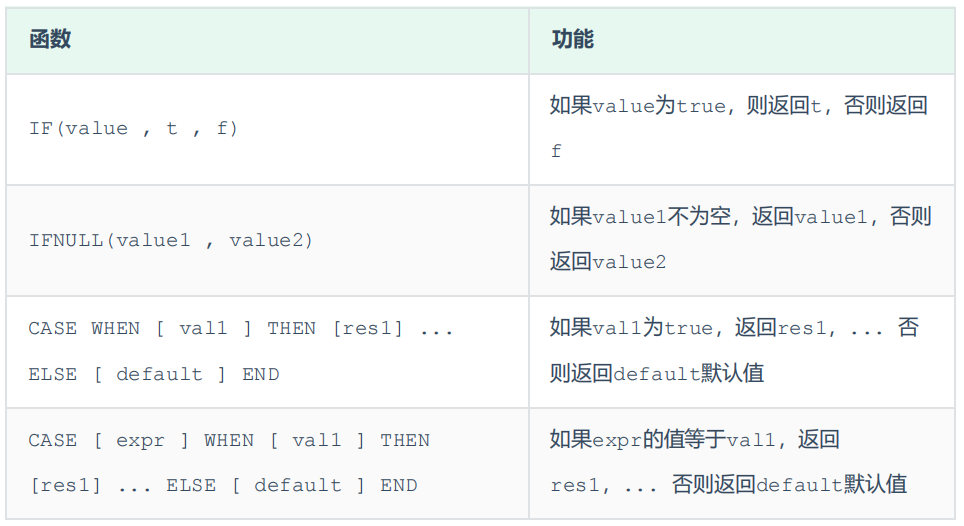
MySQL数据库中的函数怎样使用?
函数 是指一段可以直接被另一段程序调用的程序或代码。 也就意味着,这一段程序或代码在MySQL中已经给我们提供了,我们要做的就是在合适的业务场景调用对应的函数完成对应的业务需求即可。 那么,函数到底在哪儿使用呢?我们先来看两个场景&…...

命名空间的使用大全
概述 在C中,我们会使用变量、常量、函数、类、对象、结构体等各种元素。随着工程越来越庞大,代表这些元素的标识符冲突的概率也越来越大。为了解决标识符命名冲突的问题,C标准在1995年引入了关键字namespace,也叫做命名空间。使用…...

Redisson分布式锁和同步器详解-官方原版
一、锁定基于Redis的Java分布式可重入锁对象,并实现了锁接口。如果获取锁的Redisson实例崩溃,则此类锁可能会在获取状态下永久挂起。为了避免这种Redisson维护锁看门狗,当锁持有者Redisson实例处于活动状态时,它会延长锁的到期时间…...

【C语言进阶】指针与数组、转移表详解
前言 大家好我是程序猿爱打拳,我们在学习完指针的基本概念后知道了指针就是地址,我们可以通过这个地址并对它进行解引用从而改变一些数据。但只学习指针的基础是完全不够的,因此学习完指针的基础后我们可以学习关于指针的进阶,其中…...

SDN是什么,和SD-WAN有什么关系
SDN全称为“软件定义网络”(Software-Defined Networking),是一种新型的网络架构,通过将网络的控制面和数据面分离,将网络控制集中到控制器中进行统一管理和配置,以提高网络的灵活性和可管理性。传统网络的…...
)
百度前端高频react面试题(持续更新中)
说说你用react有什么坑点? 1. JSX做表达式判断时候,需要强转为boolean类型 如果不使用 !!b 进行强转数据类型,会在页面里面输出 0。 render() {const b 0;return <div>{!!b && <div>这是一段文本</div>}</div…...

中级嵌入式系统设计师2016下半年下午应用设计试题
中级嵌入式系统设计师2016下半年下午试题 试题一 阅读以下说明,回答问题1至问题3。 【说明】 某综合化智能空气净化器设计以微处理器为核心,包含各种传感器和控制器,具有检测环境空气参数(包含温湿度、可燃气体、细颗粒物等),空气净化、加湿、除湿、加热和杀菌等功能…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
