常用排序算法实现
时间复杂度
O ( 1 ) O(1) O(1)
void func1(int n){int count = 100;count++;
}
void func2(int n){int count = 100;for(int i = 0; i < count;i++){}
}
int func3(int n){return n;
}
O ( n ) O(n) O(n)
void func1(int n){int count = 100;for(int i = 0; i < n;i++){count++;}
}
O ( n 2 ) O(n^2) O(n2)
void func1(int n){int count = 100;for(int i = 0; i < n;i++){for(int j = 0;j < n;j++){count++;}}
}
O ( n m ) O(nm) O(nm)
void func1(int n,int m){int count = 100;for(int i = 0; i < n;i++){for(int j = 0;j < m;j++){count++;}}
}
O ( log n ) O(\log n) O(logn)
void func1(int n){int i = 1;while(i < n){i *= 2;}
}
O ( n log n ) O(n \log n) O(nlogn)
void func1(int n){int i = 1;for(j = 0; j < n; j++){while(i < n){i *= 2;} }
}
空间复杂度
O ( 1 ) O(1) O(1)
void func1(int n){int a = 1;a++;int b = 2;b++;
}
O ( n ) O(n) O(n)
void func1(int n){int[] array = new int[n];for(int i = 0;i < n; i++){array[i] = i;}
}int sum(int n){int a;if(n == 0) return 0;return n + sum(n - 1);
}
O ( n 2 ) O(n^2) O(n2)
void func1(int n){int[,] array = new int[n,n];
}int sum(int n){int[] array = new int[n];if(n == 0) return 0;return n + sum(n - 1);
}
稳定性和冒泡排序
稳定性:当需要排序的序列中存在相同关键字的元素,排序后的相对次序保持不变,则算法稳定,稳定的排序算法会保留数值项顺序的表达意义。
冒泡排序:
int [] array = new int[]{2,5,6,7,1,3}
void bubbleSort(int[] arr, int n){int temp;int i,j;for(i = 0;i< n - 1; i++){for(j = 0; j < n-1-i; j++){if(arr[j] > arr[j + 1]){temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}
时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1)
改进版:
int [] array = new int[]{2,5,6,7,1,3}
void bubbleSort(int[] arr, int n){int temp;int i,j;bool flag = false; for(i = 0;i< n - 1; i++){for(j = 0; j < n-1-i; j++){flag = false;if(arr[j] > arr[j + 1]){temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;flag = true;}}if(!flag){break;}}
}
选择排序
void arr_sort(int *p,int n)
{int i,j;int min = 0;for(i = 0;i < n - 1;i++)//排序次数{min = i;for(j = i + 1;j < n;j++){if(p[j] < p[min]){min = j;//记录交换的元素下标值}}if(i != min){int temp = p[i];p[i] = p[min];p[min] = temp;} }
}插入排序
int [] array = new int[]{2,5,6,7,1,3}
void printArray(int[] arr){ls = "";foreach(var r in arr){ls += r + ",";}Debug.Log("轮次" + index++ + "数组" + ls);
}
void insertSort(int[] arr, int n){for(i = 0;i< n; i++){for(j = i; j > 0 && arr[j-1] > arr[j]; j--){int temp = arr[j];arr[j] = arr[j - 1];arr[j - 1] = temp;}printArray(arr);}
}
时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1)
希尔排序
希尔排序是对插入排序的优化。
int [] array = new int[]{2,5,6,7,1,3}
void printArray(int[] arr){ls = "";foreach(var r in arr){ls += r + ",";}Debug.Log("轮次" + index++ + "数组" + ls);
}
void shellSort(int[] arr, int n){int i = 0;int j = 0;int temp;for(int step = n / 2; step > 0; step = step / 2){for(i = step; i < n; i++){temp = arr[i];for(j = i; j >= step && temp < arr[j - step]; j -= step){arr[j] = arr[j - step];} arr[j] = temp;}printArray(arr);}
}
时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( 1 ) O(1) O(1),稳定性是不稳定的
堆排序
堆是一颗完全的二叉树,堆中某个节点的值总是不大于(大顶堆)或不小于(小顶堆)其父节点的值
void heapSort(int[] list){// 构建初始堆for(int i = list.Length / 2 - 1; i >= 0; i--){AdjustHeap(list,i,list.Length); // O(n)}// 进行n-1次循环,完成排序for(int i = list.Length - 1; i > 0; i--){ // O(nlogn)// 交换堆顶(最大数)到最后,并把这个节点从二叉树去掉int temp = list[i];list[i] = list[0];list[0] = temp;// 只有堆顶不确定是不是最大,只调整堆顶即可AdjustHeap(list, 0, i);}
}
public void AdjustHeap(int[] array,int parent ,int Length){int temp = array[parent]; // 父节点int child = 2 * parent + 1; // 左子节点while(child < Length){// 找最大的子节点if(child + 1 < Length && array[child] < array[child + 1]){child++;}if(temp >= array[child])break;// 如果子节点较大,交换父子节点array[parent] = array[child];// 子节点作为父节点,进行下一轮比较parent = child;child = 2 * child + 1;}array[parent] = temp;
}
时间复杂度 O ( n log n ) O(n\log n) O(nlogn),空间复杂度 O ( 1 ) O(1) O(1),稳定性是不稳定的
二叉树排序
二叉排序树:空树或满足以下条件
- 如果左子树不空,左子树上的所有节点值均小于根节点的值。如果右子树不空,右子树上的所有节点均大于根节点的值。
- 左、右子树分别为二叉排序树。
遍历顺序:
中序遍历(左根右)、先序遍历(根左右)、后序遍历(左右根)
我们采用中序遍历,也就是说,二叉排序树从小到大的遍历顺序是从最后最左的子节点开始,往上遍历,遍历到父节点的时候,再从下往上,从左往右遍历右子节点,如此往复,遍历完左右节点。
public class BinarySortTreeNode{public int Key{get;set;}public BinarySortTreeNode Left{get;set;}public BinarySortTreeNode Right{get;set;}public BinarySortTreeNode(int key){Key = key;}public void Insert(int key){var tree = new BinarySortTreeNode(key);if(tree.Key <= Key){if(Left == null){Left = tree;}else{Left.Insert(key);}else{if(Right == null){Right = tree;}else{Right.Insert(key);}}}}// 遍历方法(妙啊)public void InorderTraversal(){Left?.InorderTraversal();Debug.Log(Key);Right?.InorderTraversal();}
}public static void BinaryTreeSort(int[] array){var binarySortTreeNode = new BinarySortTreeNode(array[0]);for(int i = 1; i < array.Length; i++){binarySortTreeNode.Insert(array[i]); }binarySortTreeNode.InorderTraversal();
}时间复杂度 O ( n log n ) O(n\log n) O(nlogn),空间复杂度 O ( n ) O(n) O(n),稳定性是不稳定的
快速排序
参考:https://blog.csdn.net/qq_40941722/article/details/94396010
void Quick_Sort(int *arr, int begin, int end){if(begin > end)return;int tmp = arr[begin];int i = begin;int j = end;while(i != j){while(arr[j] >= tmp && j > i)j--;while(arr[i] <= tmp && j > i)i++;if(j > i){int t = arr[i];arr[i] = arr[j];arr[j] = t;}}arr[begin] = arr[i];arr[i] = tmp;Quick_Sort(arr, begin, i-1);Quick_Sort(arr, i+1, end);
}function Sort(list, leftIndex, rightIndex)if(leftInfex >= rightIndex) thenreturnendlocal i = leftIndexlocal j = rightIndexlocal baseValue = list[leftIndex]while i < j dowhile i < j and list[j] >= baseValue doj = j - 1endwhile i < j and list[i] <= baseValue doi = i + 1endif j > i thent = list[i];list[i] = list[j];list[j] = t;endendlist[leftIndex] = list[i];list[i] = baseValue;Quick_Sort(list, leftIndex, i-1);Quick_Sort(list, i+1, rightIndex);
end快速排序最优时间复杂度为O(nlogn),不稳定
归并排序
参考:https://www.bilibili.com/video/BV1Pt4y197VZ/
function sort(arr, startIndex = 0, endIndex = arr.length - 1) {// 递归结束条件:startIndex大于等于endIndex的时候if (startIndex >= endIndex) {return;}// 折半递归let midIndex = parseInt((startIndex + endIndex) / 2);sort(arr, startIndex, midIndex);sort(arr, midIndex + 1, endIndex);// 将两个有序的小数组,合并成一个大数组merge(arr, startIndex, midIndex, endIndex);
}function merge(arr, startIndex, midIndex, endIndex) {// 新建一个大数组let tempArr = [];let p1 = startIndex;let p2 = midIndex + 1;let p = 0;// 比较两个有序小数组的元素,依次放入大数组中while (p1 <= midIndex && p2 <= endIndex) {if (arr[p1] <= arr[p2]) {tempArr[p++] = arr[p1++];} else {tempArr[p++] = arr[p2++];}}// 右侧小数组已排序完毕,左侧小数组还有剩余,将左侧小数组元素依次放入大数组尾部while (p1 <= midIndex) {tempArr[p++] = arr[p1++];}// 左侧小数组已排序完毕,右侧小数组还有剩余,将右侧小数组元素依次放入大数组尾部while (p2 <= endIndex) {tempArr[p++] = arr[p2++];}for (let i = 0; i < tempArr.length; i++) {arr[i + startIndex] = tempArr[i];}
}let arr = [4, 5, 8, 1, 7, 2, 6, 3];
sort(arr);
console.log(arr);时间复杂度是O(nlogn),稳定
排序算法的使用场景
- 游戏中得分排行榜
- 英雄战力榜列表等
拓扑排序
拓扑排序(Topological Sorting)是一种对有向无环图(Directed Acyclic Graph, DAG)进行排序的算法。在拓扑排序中,节点表示图中的任务或事件,有向边表示任务间的依赖关系。
拓扑排序的目标是将图中的节点按照一定的顺序线性排列,使得所有的依赖关系都得到满足。也就是说,在排序结果中,若存在一条从节点 A 到节点 B 的有向边,那么节点 A 在排序中必须出现在节点 B 之前。
通俗讲解:当同时存在很多件事情需要完成,但是有些事情的完成依赖于另外若干件事情的完成,拓扑排序需要我们排列出事情完成的顺序,这个顺序往往不止一种。
拓扑排序的算法通常使用深度优先搜索(DFS)或广度优先搜索(BFS)来实现。在实际应用中,如果图中存在环路(即有向图中存在回路),则无法进行拓扑排序,因为无法满足所有的依赖关系。因此,拓扑排序算法通常要求应用于有向无环图。
步骤
- 构建图:根据给定的有向图的边关系,构建表示图的数据结构。通常使用邻接表或邻接矩阵表示图。
- 统计节点入度:对于每个节点,统计它的入度(即指向该节点的边的数量)。可以通过遍历图的边关系,记录每个节点的入度。
- 初始化队列:创建一个队列(可以使用队列数据结构),用于存储入度为0的节点。
- 入度为0的节点入队:遍历所有节点,将入度为0的节点加入队列。
- 拓扑排序:从队列中取出一个节点,输出该节点(或保存到结果序列中),并将其相邻节点的入度减1。若某个节点的入度减为0,则将其加入队列。
- 重复步骤5,直到队列为空。如果输出的节点数量与图中的节点数量相同,则拓扑排序成功;否则,图中存在环路,无法进行拓扑排序。
- 输出结果:按照拓扑排序的顺序输出节点,即为拓扑排序的结果。
int topological_sort(LGraph G)
{int i,j;int index = 0;int head = 0; // 辅助队列的头int rear = 0; // 辅助队列的尾int *queue; // 辅组队列int *ins; // 入度数组char *tops; // 拓扑排序结果数组,记录每个节点的排序后的序号。int num = G.vexnum;ENode *node;ins = (int *)malloc(num*sizeof(int)); // 入度数组tops = (char *)malloc(num*sizeof(char));// 拓扑排序结果数组queue = (int *)malloc(num*sizeof(int)); // 辅助队列assert(ins!=NULL && tops!=NULL && queue!=NULL);memset(ins, 0, num*sizeof(int));memset(tops, 0, num*sizeof(char));memset(queue, 0, num*sizeof(int));// 统计每个顶点的入度数for(i = 0; i < num; i++){node = G.vexs[i].first_edge;while (node != NULL){ins[node->ivex]++;node = node->next_edge;}}// 将所有入度为0的顶点入队列for(i = 0; i < num; i ++)if(ins[i] == 0)queue[rear++] = i; // 入队列while (head != rear) // 队列非空{j = queue[head++]; // 出队列。j是顶点的序号tops[index++] = G.vexs[j].data; // 将该顶点添加到tops中,tops是排序结果node = G.vexs[j].first_edge; // 获取以该顶点为起点的出边队列// 将与"node"关联的节点的入度减1;// 若减1之后,该节点的入度为0;则将该节点添加到队列中。while(node != NULL){// 将节点(序号为node->ivex)的入度减1。ins[node->ivex]--;// 若节点的入度为0,则将其"入队列"if( ins[node->ivex] == 0)queue[rear++] = node->ivex; // 入队列node = node->next_edge;}}if(index != G.vexnum){printf("Graph has a cycle\n");free(queue);free(ins);free(tops);return 1;}// 打印拓扑排序结果printf("== TopSort: ");for(i = 0; i < num; i ++)printf("%c ", tops[i]);printf("\n");free(queue);free(ins);free(tops);return 0;
}
其中G是有向图,结构可能如下:
struct ENode
{int ivex; // 该边所指向的顶点的位置struct ENode *next_edge; // 指向下一条弧的指针
} ;struct VNode
{char data; // 顶点的数据ENode *first_edge; // 指向第一条依附该顶点的边的指针
} ;struct struct
{VNode vexs[MAX_VERTEX_NUM]; // 顶点数组int vexnum; // 顶点数量int edgenum; // 边数量
} ;
相关文章:

常用排序算法实现
时间复杂度 O ( 1 ) O(1) O(1) void func1(int n){int count 100;count; } void func2(int n){int count 100;for(int i 0; i < count;i){} } int func3(int n){return n; }O ( n ) O(n) O(n) void func1(int n){int count 100;for(int i 0; i < n;i){count;} …...

使用表单登录方法模拟登录通信人家园,要求发送登录请求后打印出来的用户名下的用户组类别
目标网站:https://www.txrjy.com/forum.php 一、进入网页,右键“检查” 二、输入用户名和密码,点击“登录”,点击“Network”,上划加载项找到蓝色框中的内容 三、点击第一个加载项,找到URL 四、相关代码: …...
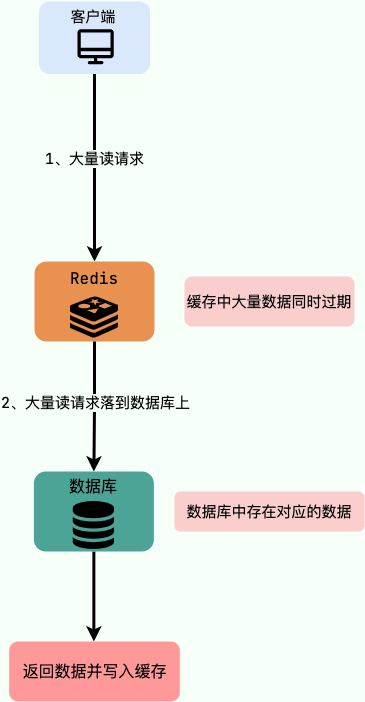
Redis 的缓存击穿,穿透,雪崩及其解决方案
1 缓存穿透 什么是缓存穿透? 大量请求的 key 是不合理的,根本不存在于缓存中,也不存在于数据库中 。导致这些请求直接到了数据库上,根本没有经过缓存这一层,对数据库造成了巨大的压力,可能直接就被这么多…...
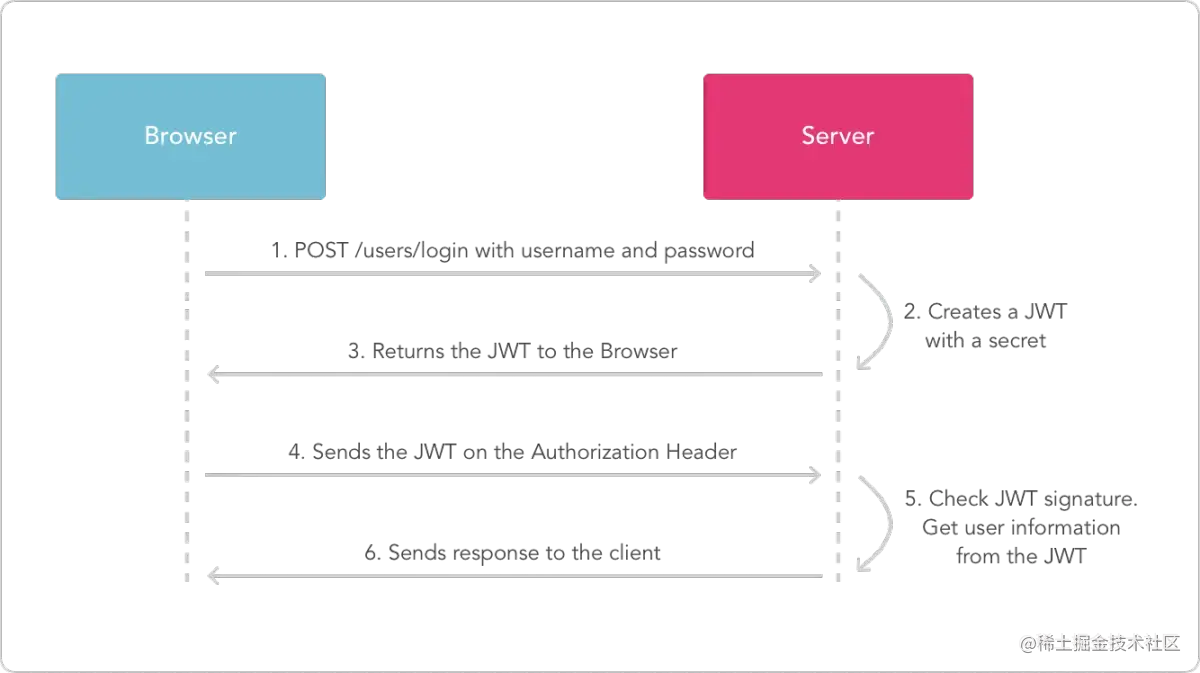
JWT原理分析——JWT
了解为什么会有JWT的出现? 首先不得不提到一个知识叫做跨域身份验证,JWT的出现就是为了更好的解决这个问题,但是在没有JWT的时候,我们一般怎么做呢?一般使用Cookie和Session,流程大体如下所示:…...
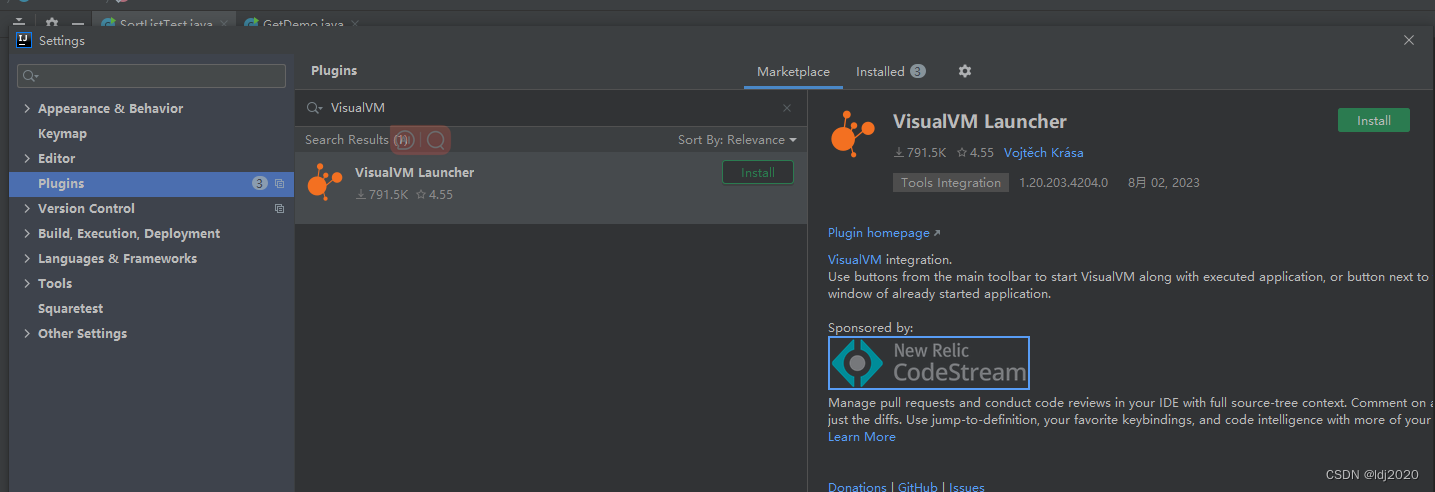
Jprofiler/ VisualVM 定位内存溢出OOM
下载,接受协议下一步下一步,最后选择与IDEA集成OK ej-technologies - Java APM, Java Profiler, Java Installer Builder IDEA配置参数: # F:\study\spring-test\dump 为dump文件保存路径-XX:HeapDumpOnOutOfMemoryError -XX:HeapDumpPathF:\study\spring-test\dumppackage …...

NOIP2023模拟13联测34 competition
题目大意 有一场题目数量为 m m m的比赛,有一个团队想要来参加。 这个团队有 n n n个选手,编号为 i i i的选手能做第 l i ∼ r i l_i \sim r_i li∼ri道题,每题他都有 100 % 100\% 100%的概率做出来。 这个团队会随机派出一只队伍来参…...
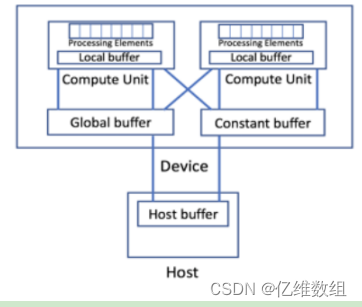
Intel oneAPI笔记(2)--jupyter官方文档(oneAPI_Intro)学习笔记
前言 本文是对jupyterlab中oneAPI_Essentials/01_oneAPI_Intro文档的学习记录,包含对SYCL、DPC extends SYCL、oneAPI Programming models等介绍和SYCL代码的初步演示等内容 oneAPI编程模型综述 oneAPI编程模型提供了一个全面而统一的开发人员工具组合࿰…...
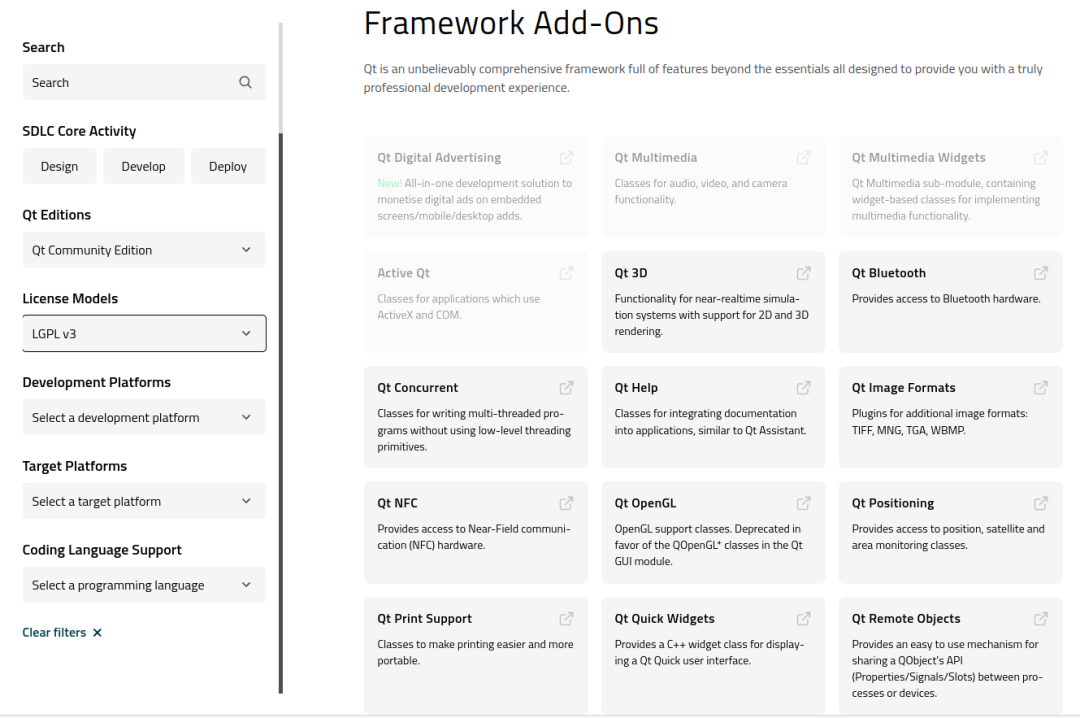
用 QT 开发软件会吃官司吗?
之前我写过我们现在使用 QT 开发跨平台软件,有朋友留言,QT 虽好,当心收到律师函。今天就来聊聊这个话题。 在开始这个话题之前,我们先把使用盗版 QT 排除在外,只讨论在合法且遵从版权协议的前提下,能否使用…...

远程运维用什么软件?可以保障更安全?
远程运维顾名思义就是通过远程的方式IT设备等运行、维护。远程运维适用场景包含因疫情居家办公,包含放假期间出现运维故障远程解决,包含项目太远需要远程操作等等。但远程运维过程存在一定风险,安全性无法保障,所以一定要选择靠谱…...

数据结构与算法C语言版学习笔记(2)-线性表、顺序存储结构的线性表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 数据结构部分的知识框架一、线性表的定义和特点1.定义2.特点 二、线性表的实际案例引入1.案例一:多项式的加减乘除2.案例二:当多项式是稀疏多…...
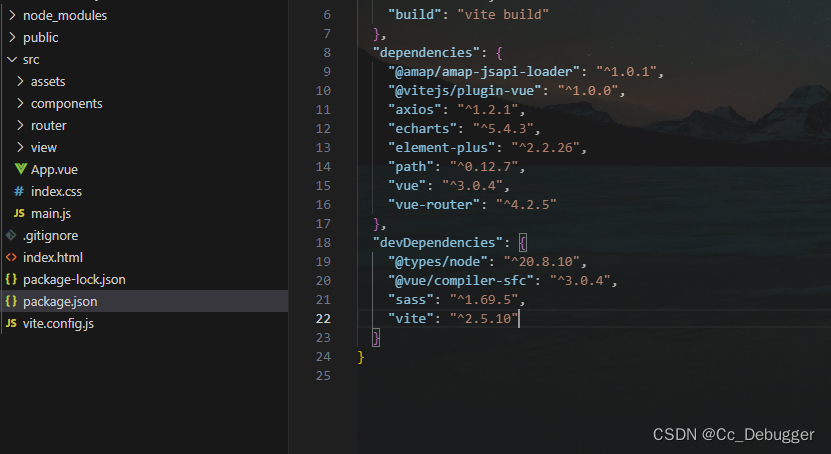
【vite】vite.defineConfig is not a function/npm无法安装第三方包问题
当使用vite命令 npm init vite-app 项目名称时配置 import vue from vitejs/plugin-vueexport default defineConfig({plugins: [vue()] })会报错vite.defineConfig is not a function 还有就是npm下载的时候也会报错 原因vite插件vitejs/plugin-vue和vite版本问题 解决 调…...

234. 回文链表 --力扣 --JAVA
题目 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 解题思路 判断链表是否为回文链表取决于链表中各个节点的值,所以可以通过存储各节点的值进行对比判断&…...
【JAVA学习笔记】65 - 文件类,IO流--节点流、处理流、对象流、转换流、打印流
项目代码 https://github.com/yinhai1114/Java_Learning_Code/tree/main/IDEA_Chapter19/src/com/yinhai 文件 一、文件,流 文件,对我们并不陌生,文件是保存数据的地方,比如大家经常使用的word文档,txt文件,excel文件..都是文件。它既可以保存一张图片…...

R语言 复习 习题图片
这是日天土申哥不知道从哪淘来的R语言复习知识点图片,大部分内容都是课后习题的答案 加油吧,骚年,考个好分数...
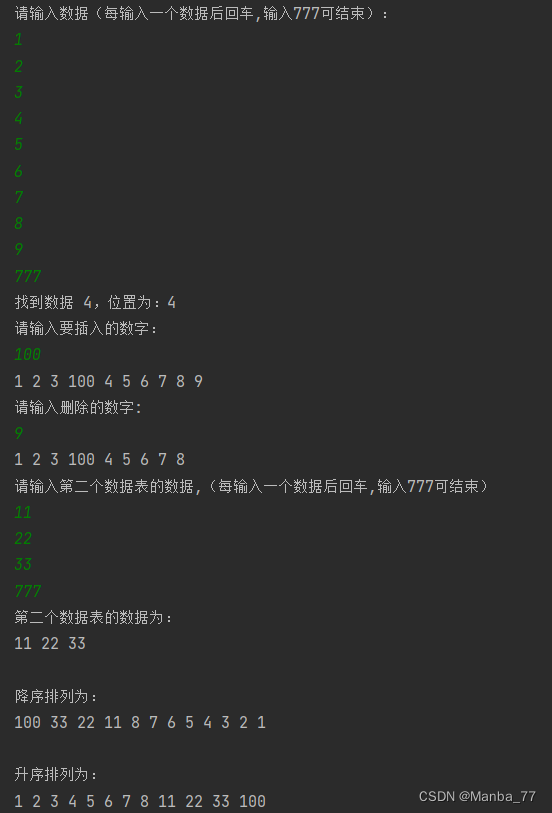
c语言 结构体 简单实例
结构体 简单例子 要求: 结构体保存学生信息操作 代码 #include <stdio.h>//定义结构体 struct student{int ID;char name[20];char sex;char birthday[8];int grade; };int main(){int number;printf("请输入学生个数:");scanf(&quo…...

【ChatGPT】ChatGPT的自定义指令
ChatGPT的自定义指令 关于ChatGPT自定义指令的常见问题解答概述可用性如何使用您的数据自定义指令设置将应用于所有新聊天。启动新聊天可查看更改iOS & AndroidWeb 示例常见问题使用自定义指令的好处字符限制我的ChatGPT数据导出中是否包含自定义指令?当我删除我…...

《哥德尔、艾舍尔、巴赫——集异璧之大成》阅读笔记1
1、谁也不知道非智能行为和智能行为之间的界限在哪里。事实上,认为存在明显界限也许是愚蠢的。但是智能的基本能力还是确定的,它们是: 对于情境有很灵活的反应充分利用机遇弄懂含糊不清或彼此矛盾的信息认识到一个情境中什么是重要的因素&am…...

稳定细胞系构建技术介绍
抗体药物的开发是一个非常复杂的过程,构建适用于工业生产的高表达的稳定细胞株是抗体药工艺开发的起点和基础。一株稳定高产的工程细胞株不仅能显著增加单位体积产量,降低生产成本,还可以降低下游纯化工艺复杂度,确保获得安全&…...
k8s部署srs服务
k8s部署srs服务 项目需要把srs纳入k8s进行管理,需要通过k8s来部署srs服务然后原本的srs可以支持rtmp与webrtc两种,官网查了部署方式,k8s只有最基本的部署方式于是开始研究k8s部署能够正常推拉流的webrtc版本的srs 首先肯定是去官网查有无相关…...

使用Java分割PDF文件
在Java中,我们可以使用iText库来处理PDF文件。iText是一个流行的Java库,用于创建和处理PDF文件。在本篇博客中,我们将介绍如何使用Java分割一个PDF文件为多个小的PDF文件。 1. 引入iText依赖 首先,我们需要在项目中引入iText库的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
