视频转码教程:轻松制作GIF动态图,一键高效剪辑操作
随着社交媒体的兴起,GIF动态图已经成为了人们表达情感、分享精彩瞬间的重要方式。而将视频转化为GIF动态图,不仅可以方便地在社交媒体上分享,还可以延长视频的播放时长,吸引更多的观众。本篇文章将为大家介绍如何将视频轻松转化为GIF动态图,帮助大家更好地分享自己的视频内容。

操作1首先在云炫AI智剪面板上点击“智能转码”功能,切换到主编辑面板中。

操作2、这一步需要把原视频的素材导入到列表中。先点击“添加视频文件夹”,在弹出的对话框内选择原素材路径,并点击“确定”。

操作3、选择转码的模式,有“转为H264和265编码、序列图片、gif动图、MP3音频、MP4视频、FLV视频等”。这些可根据要求来选择,我们这里选择“转为gif动图”就可以了。

操作4、现在设置保存位置,点击“浏览”选择新视频保存路径后,再点击“确定”。

操作5、都设定好之后就可以点击“开始转码”进行动态图转换。

操作6、这个过程速度会慢些,可以通过状态栏或滚动条查看转码进度的情况。

操作7、转码完成后,点击“打开文件夹”就能看到已转码的gif动态图。

操作8、打开gif图片,效果还不错,动作流畅,说明转码成功。

相关文章:

视频转码教程:轻松制作GIF动态图,一键高效剪辑操作
随着社交媒体的兴起,GIF动态图已经成为了人们表达情感、分享精彩瞬间的重要方式。而将视频转化为GIF动态图,不仅可以方便地在社交媒体上分享,还可以延长视频的播放时长,吸引更多的观众。本篇文章将为大家介绍如何将视频轻松转化为…...
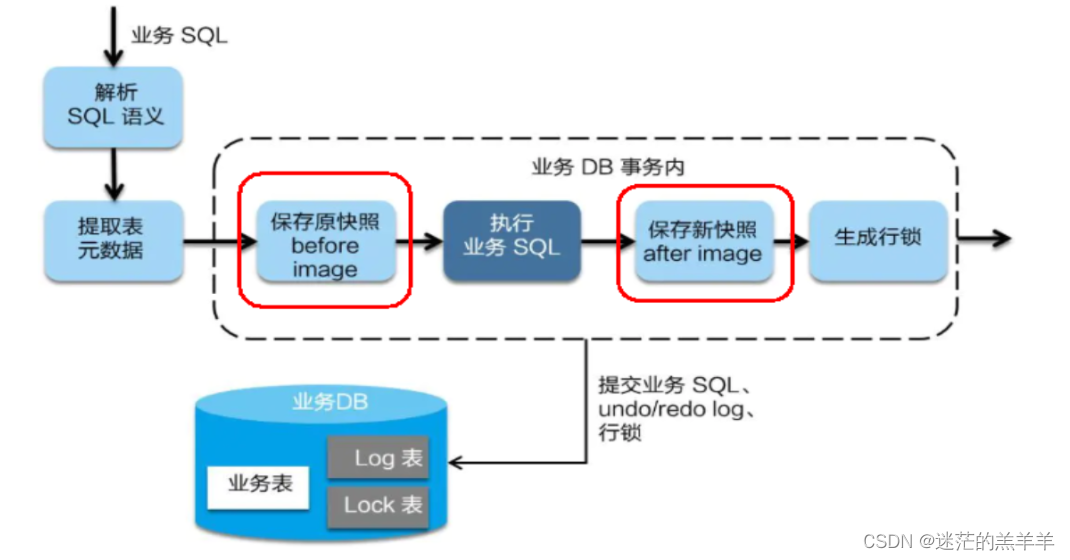
Seata分布式事务实现原理
Seata可以解决分布式事务问题,利用GlobalTransacational(name "fsp-create-order",rollbackFor Exception.class)注解就可以实现全局的事务管理,但是我们需要明白原理的实现。 我们举例创建订单——>调减库存——>调扣余额——>改订…...

Rasa NLU中的组件
Rasa NLU部分主要是解决NER(序列建模)和意图识别(分类建模)这2个任务。Rasa NLP是一个基于DAG的通用框架,图中的顶点即组件。组件特征包括有顺序关系、可相互替换、可互斥和可同时使用。有向无环图(DAG&…...
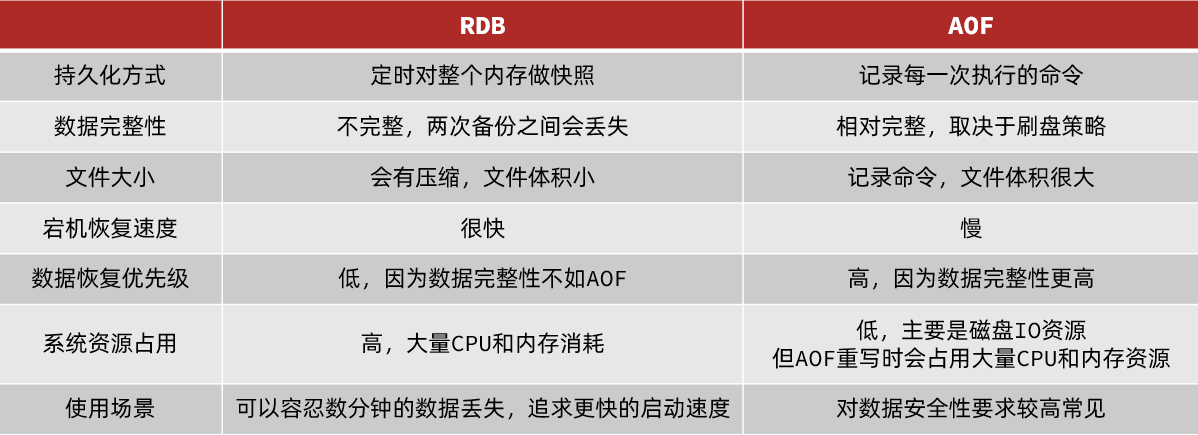
redis笔记 三 redis持久化
文章目录 Redis持久化RDB持久化执行时机RDB原理小结 AOF持久化AOF原理AOF配置AOF文件重写 RDB与AOF对比 Redis持久化 redis持久化是为了解决redis宕机时丢失数据的问题,Redis有两种持久化方案: RDB持久化AOF持久化 RDB持久化 RDB全称Redis Database …...

k8s-----数据存储
目录 一、数据存储的概念 二、基本存储 1、EmptyDir存储卷 2、hostPath存储卷 3、nfs共享存储卷 三、高级存储 1、PV(持久化卷) 2、PVC(持久化卷声明) 3、静态PV实验 4、动态PV实验 4.1 在stor01节点上安装nfs…...
macOS电池续航工具:Endurance中文
Endurance for Mac是一款强大而实用的电池管理和优化软件,专为MacBook设计。通过智能调整系统设置和管理后台应用,它能有效延长电池续航时间,提升工作和娱乐效率,成为你在各种场合下的得力助手。 Endurance for Mac软件的功能特色…...

栈(定义,基本操作,顺序存储,链式存储)
目录 1.栈的定义1.重要术语2.特点 2.栈的基本操作3.栈的顺序存储1.顺序栈的定义2.基本操作1.初始化2.进栈3.出栈4.读栈顶 3.共享栈 4.栈的链式存储 1.栈的定义 栈( Stack)是只允许在一端进行插入或删除操作的线性表。 一种受限的线性表,只能在栈顶进行插…...
在HTML单页面中,使用Bootstrap框架的多选框如何提交数据
1.引入Bootstrap CSS和JavaScript文件:确保在HTML页面的标签内引入Bootstrap的CSS和JavaScript文件。可以使用CDN链接或者下载本地文件。 <link rel"stylesheet" href"https://maxcdn.bootstrapcdn.com/bootstrap/4.5.2/css/bootstrap.min.css&q…...
当爱好变成职业,会不会就失去了兴趣?
当爱好变成职业,会不会就失去了兴趣? 当兴趣变成职业 1、学习能力变强了,积极主动性增加了。 2、学习努力变现了,赚到的更钱多了。 3、赚钱能力变强了,反过来再次促使兴趣发展(兴趣更大了....干劲更足了&…...
3-知识补充-MVC框架
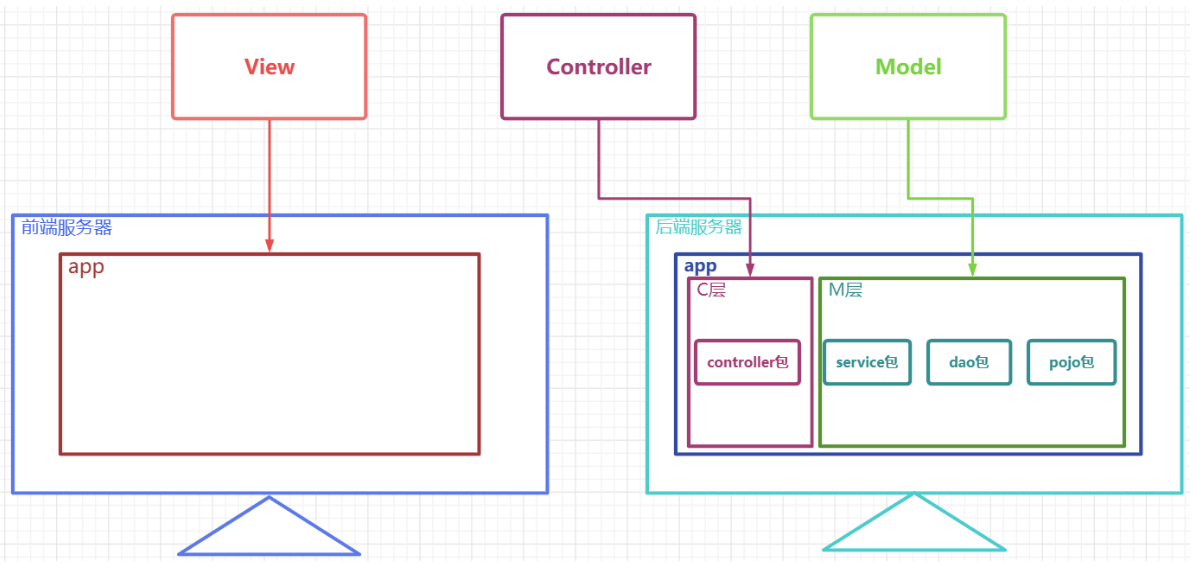
3-知识补充-MVC框架 文章目录 3-知识补充-MVC框架MVC概述M、V、C各自负责功能及常用包MVC框架图非前后端分离框架图前后端分离框架图 MVC概述 MVC(Model、View、Controller)是软件工程中的一种**软件架构模式,它把软件系统分为模型、视图和控…...
leetcode:141. 环形链表
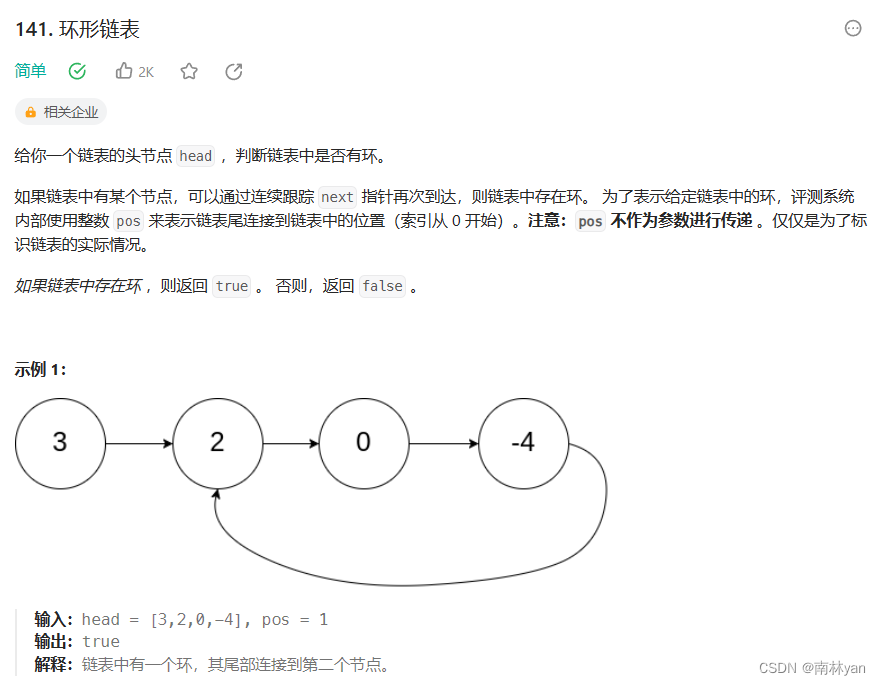
一、题目 函数原型: bool hasCycle(struct ListNode *head) 二、算法 判断不是环形链表,只需遍历链表找到空结点即可。 判断是环形链表,由于链表是环形的,遍历不会永远不会结束。所以要设置快慢指针,慢指针一次走一步&…...
了解企业邮箱的外观和功能特点
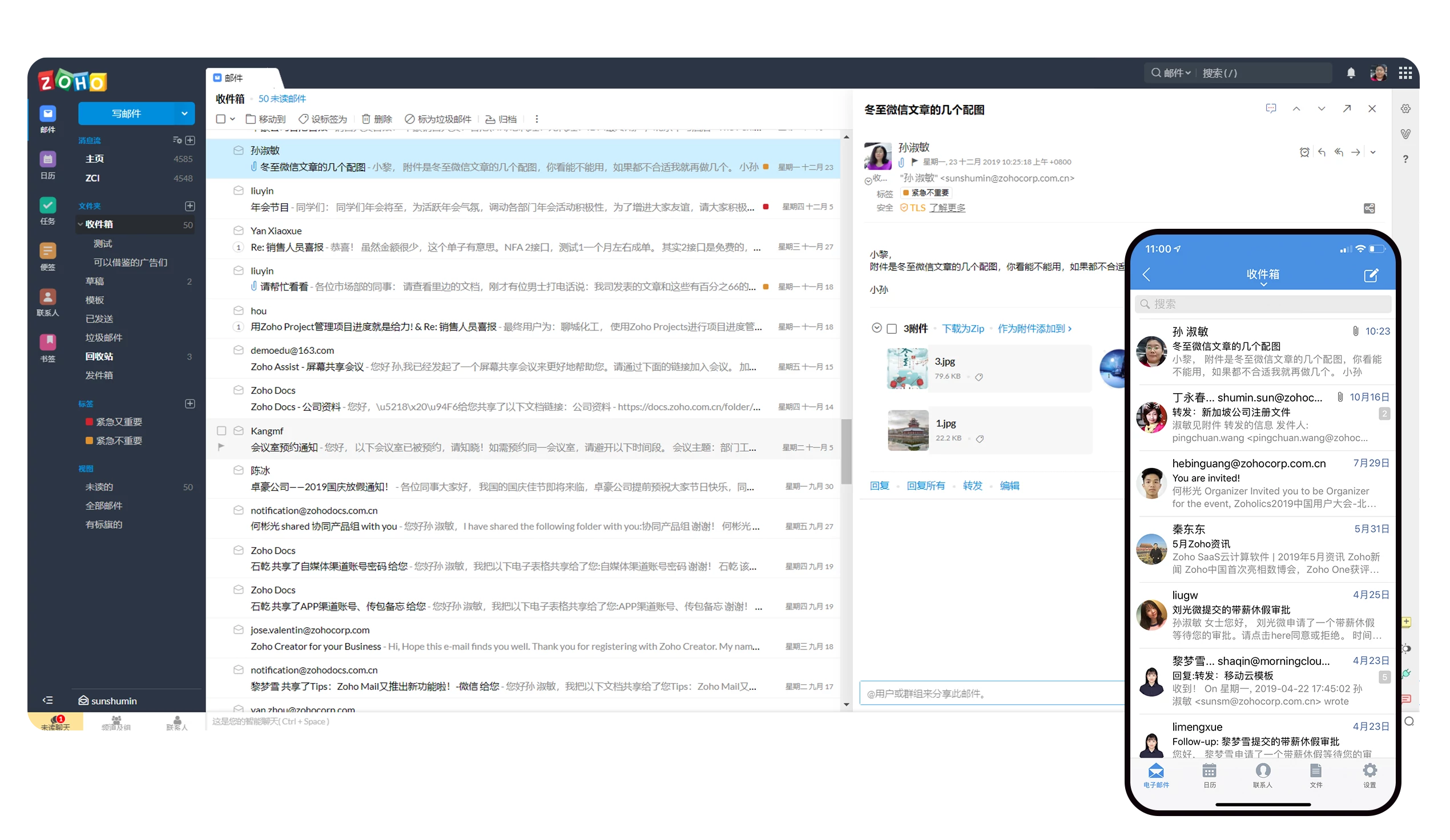
企业邮箱是什么样子的?企业邮箱不是单一产品,而是由一系列电子邮件服务组成的生态系统。这些服务包括但不限于邮件服务器、客户端、安全解决方案等。这些服务共同构成了企业邮箱的基础设施。 在外观上,企业邮箱和个人邮箱没有太大区别。用户通…...
配置阿里云镜像加速器 -docker
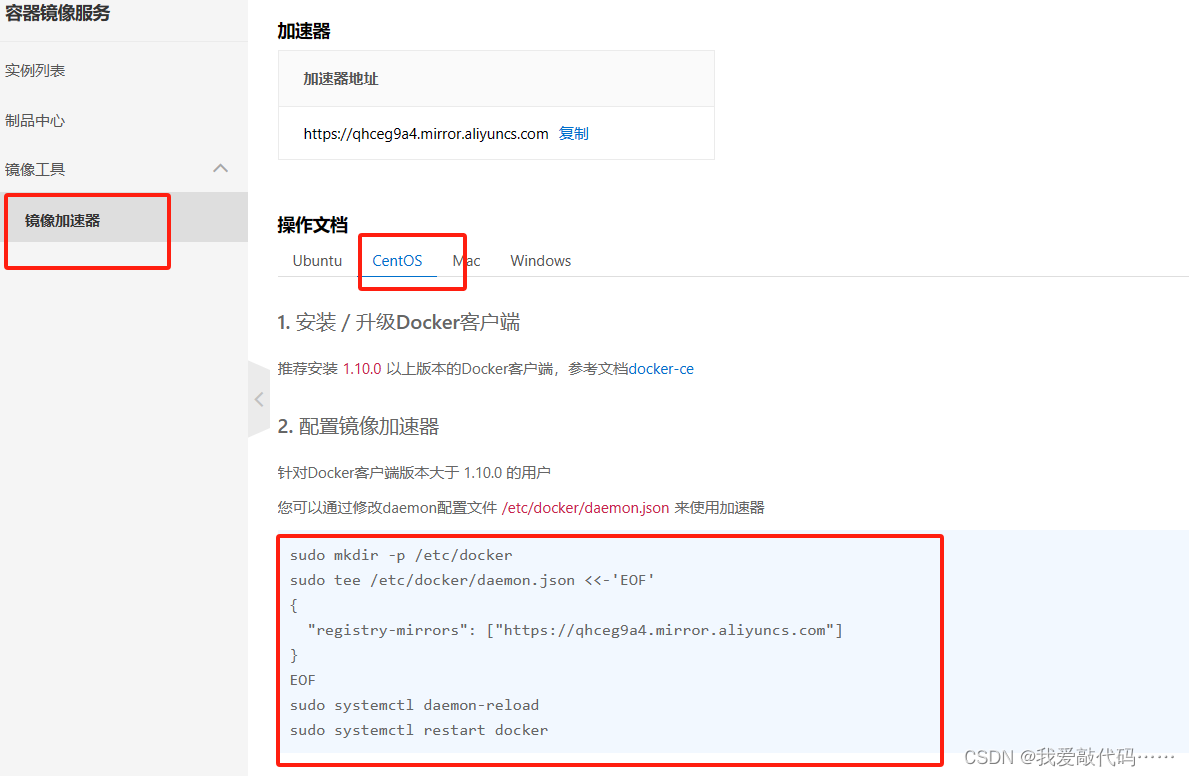
1.百度aliyun 2.找到镜像服务ACR 3.搞一个个人版,身份验证一下就行了很简单 4.找到镜像加速器Centos 5.执行下面4条命令:4条命令直接从上面操作文档中粘贴,不容易出错 sudo mkdir -p /etc/docker sudo tee /etc/docker/daemon.json <<…...

11 抽象向量空间
抽象向量空间 向量是什么函数什么是线性推论向量空间 这是关于3Blue1Brown "线性代数的本质"的学习笔记。 向量是什么 可以是一个箭头,可以是一组实数,即一个坐标对。 箭头在高维(4维,甚至更高)空间&…...

干洗店洗鞋店管理系统app小程序;
干洗店洗鞋店管理系统是一款专业的洗衣店管理软件,集成了前台收费收银系统、会员卡管理系统和财务报表系统等强大功能。界面简洁优美,操作直观简单。这款系统为干洗店和洗衣店提供了成本分析、利润分析、洗衣流程管理等诸多实用功能,用全新的…...

NOIP2023模拟13联测34 总结
NOIP2023模拟13联测34 总结 文章目录 NOIP2023模拟13联测34 总结比赛过程题目A. origen题目大意思路 B.competition题目大意思路 C. tour题目大意 D.abstract题目大意 比赛过程 看了一下题,感觉就 T 2 T2 T2 有一点思路。 T 1 T1 T1 先打一个 30 30 30 分暴力&am…...

Python武器库开发-常用模块之subprocess模块(十九)
常用模块之subprocess模块(十九) subprocess模块介绍 subprocess 模块允许我们启动一个新进程,并连接到它们的输入/输出/错误管道,从而获取返回值。subprocess 它可以用来调用第三方工具(例如:exe、另一个python文件、命令行工具…...

java验证 Map 的 key、value 是否可以为空
1、验证示例代码 Map<String, Object> maps new HashMap<>();maps.put("a", "1");maps.put(null, null);maps.put("c", null);System.out.println("maps " maps);Object o maps.get(null);System.out.println("o…...

编写MBR主引导记录
BIOS 检测,初始化硬件。挑一些重要的,能保证计算机能运行那些硬件的基本IO操作。 唤醒BIOS 唤醒BIOS需要知道其入口地址,在最后将跳转到0x7c00处 接电的一瞬间,cs:ip寄存器被初始化为0xF000:0xFFF0,所以等效地址是0…...

从零开始搭建React+TypeScript+webpack开发环境-自定义配置化的模拟服务器
技术栈 我们将使用Node.js和Express.js作为我们的后端框架,以及Node.js的文件系统(fs)模块来操作文件和文件夹。此外,我们将使用Node.js的require和delete require.cache来加载和更新模拟数据。 项目结构 首先,让我们定义一个简单的项目结…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
