机器学习基础之《回归与聚类算法(5)—分类的评估方法》
问题:上一篇的案例,真的患癌症的,能被检查出来的概率?
一、精确率和召回率
1、混淆矩阵
在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适用于多分类)
预测结果:是预测值
正确标记:是真实值
用来求精确率和召回率的
TP = True Possitive
FN = False Negative
FP = False Possitive
TN = True Negative
2、精确率(Precision)与召回率(Recall)
精确率:预测结果为正例样本中真实为正例的比例
即是,TP / (TP + FP)
召回率:真实为正例的样本中预测结果为正例的比例
即是,TP / (TP + FN)
3、真的患癌症的,能被检查出来的概率 - 召回率
二、F1-score
1、反映了模型的稳健性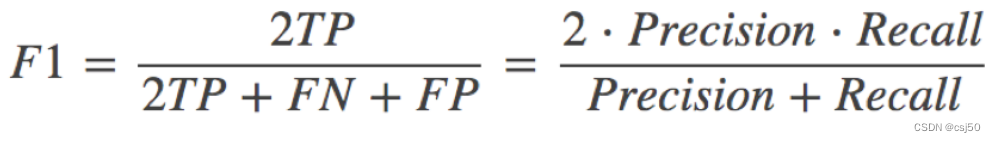
等价于:2*精确率*召回率 / (精确率 + 召回率)
Precision是预测的好瓜中有多少真正的好瓜,Recall是所有真正的好瓜被预测对了多少
三、分类评估报告API
1、sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None)
y_true:真实目标值
y_pred:估计器预测目标值
labels:指定类别对应的数字
我们在传y_true、y_pred传的是数字,将数字表示出来
target_names:目标类别名称
分类报告显示
return:每个类别精确率与召回率
2、在上一篇代码后添加
# 查看精确率、召回率、F1-score
from sklearn.metrics import classification_reportreport = classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"])print(report)运行结果: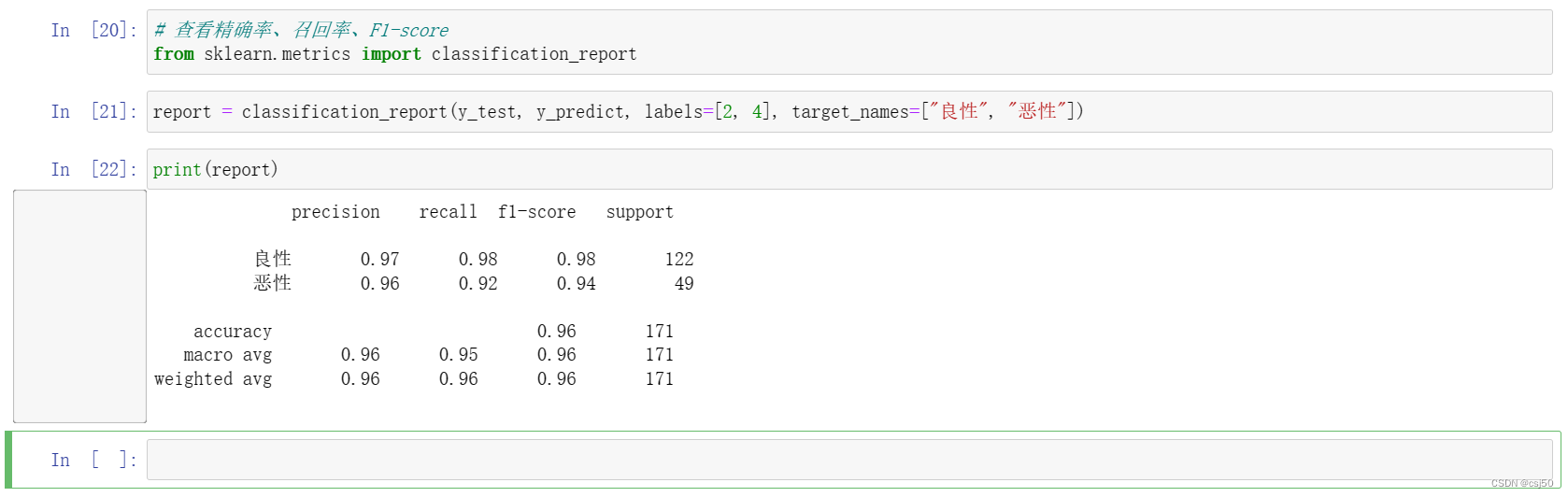
support是样本数量
四、样本不均衡的情况
1、假设这样一个情况,总共有100个人,如果99个样本癌症,1个样本非癌症,不管怎样我全都预测正例(默认癌症为正例),准确率就为99%但是这样效果并不好,这就是样本不均衡下的评估问题
准确率:99%
召回率:99 / 99 = 100%
精确率:99 / 100 = 99%
F1-score:2*99%*100% / 199% = 99.497%
就是瞎猜,全都蒙成换了癌症,不负责任的模型
这种情况我们是要避免的,我们目前学习到的这些分类指标都不能反映出它的问题所在
样本不均衡,正样本太多,反例太少
五、ROC曲线与AUC指标
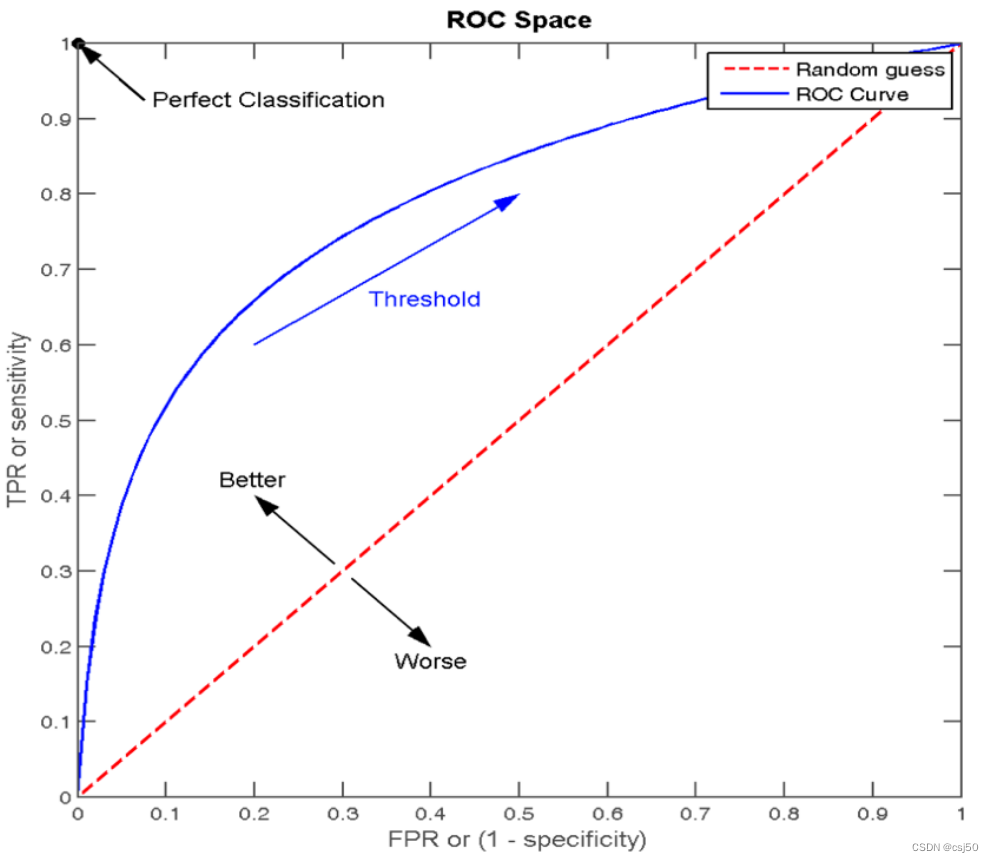
1、ROC曲线
蓝色的线是ROC曲线
2、AUC指标
ROC曲线和x轴、y轴包成的区域的面积
衡量好坏,我们看的是AUC指标,AUC越接近1越好,越接近0.5越不好
3、ROC曲线是怎么来的
TPR = TP / (TP + FN) - 就是召回率
所有真实类别为1的样本中,预测类别为1的比例
FPR = FP / (FP + FN)
所有真实类别为0的样本中,预测类别为1的比例
TPR是正例的召回率,FPR是反例的召回率
ROC曲线就是由TPR和FPR这两个指标构成的
当TPR=FPR:
正例的召回率、反例的召回率都为1,说明是在瞎猜,就是红色的斜线,面积是 1*1/2 = 0.5
当TPR>FPR:
TPR接近于1,FPR接近于0,就是接近于Perfect Classification,面积是 1*1=1
当TPR<FPR:
就是一条反曲线,做反向预测用
4、AUC的意义
(1)AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率
(2)AUC的最小值为0.5,最大值为1,取值越高越好
(3)AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器
(4)0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值
(5)最终AUC的范围在[0.5, 1]之间,并且越接近1越好
六、AUC的计算API
1、sklearn.metrics.roc_auc_score(y_true, y_score)
计算ROC曲线面积,即AUC值
y_true:每个样本的真实类别,必须传0(反例),1(正例)
y_score:可以是预测得分,可以是正例的估计概率、置信值或者分类器方法的返回值
2、代码
y_test.head()# y_true:每个样本的真实类别,必须传0(反例),1(正例)
# 将y_test转换成0,1
y_true = np.where(y_test > 3, 1, 0)y_truefrom sklearn.metrics import roc_auc_scoreroc_auc_score(y_true, y_predict)运行结果: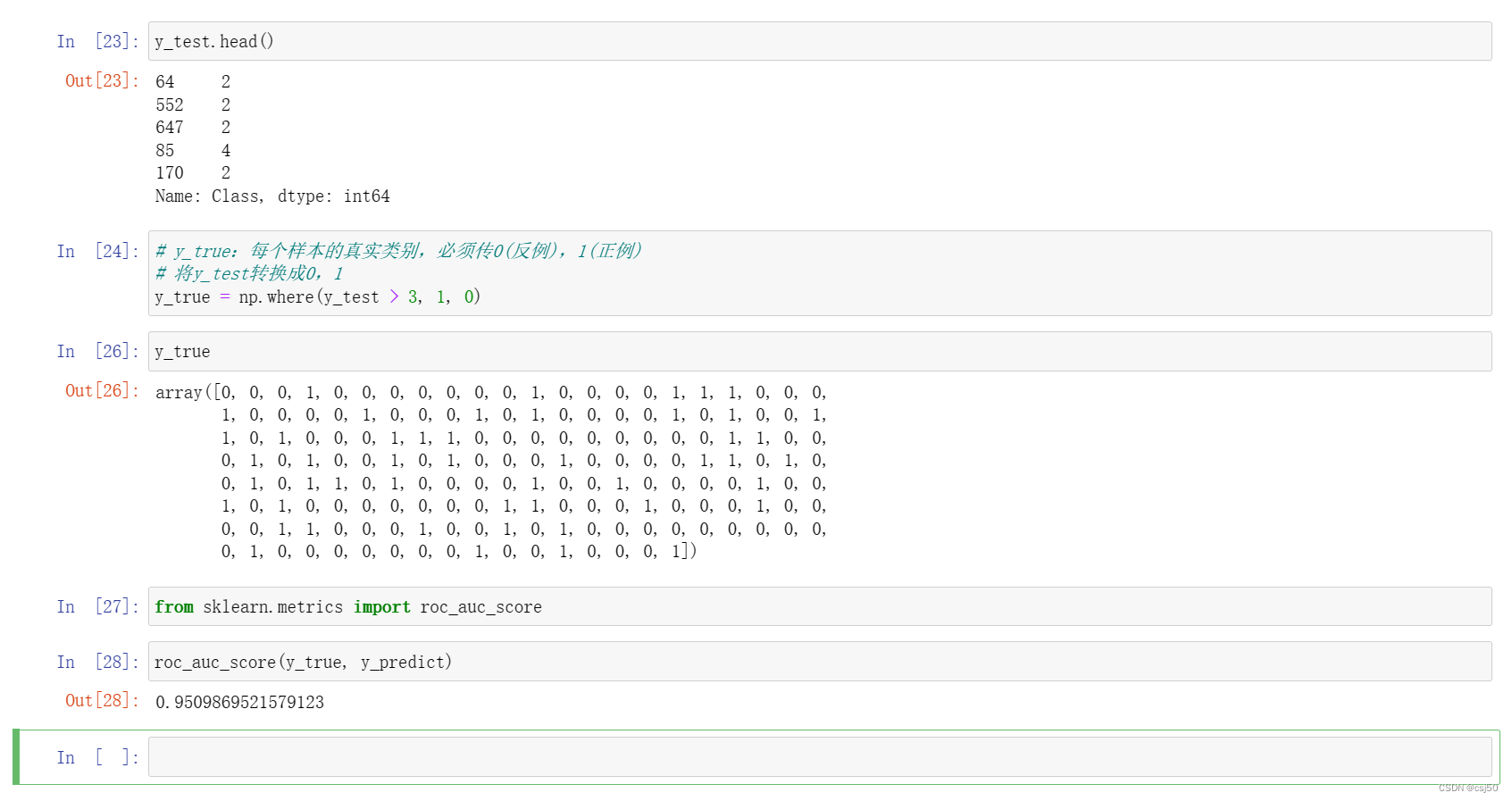
七、小结
AUC只能用来评价二分类
AUC非常适合评价样本不平衡中的分类器性能
相关文章:

机器学习基础之《回归与聚类算法(5)—分类的评估方法》
问题:上一篇的案例,真的患癌症的,能被检查出来的概率? 一、精确率和召回率 1、混淆矩阵 在分类任务下,预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合,构成混淆矩阵(适…...

如何在macbook上删除文件?Mac删除文件的多种方法
在使用MacBook电脑时,桌面上经常会积累大量的文件,而这些文件可能已经不再需要或已经过时。为了保持桌面的整洁和提高电脑性能,我们需要及时删除这些文件。本文将介绍MacBook怎么删除桌面文件,以及macbook删除桌面文件快捷键。 一…...

Java代码Demo——Map根据key或value排序
Map根据key排序 升序 Demo代码: //使用TreeMap Map<Integer, String> map new TreeMap<>(); map.put(10, "第10名次"); map.put(15, "第15名次"); map.put(1, "第1名次"); map.put(5, "第5名次"); map.put…...
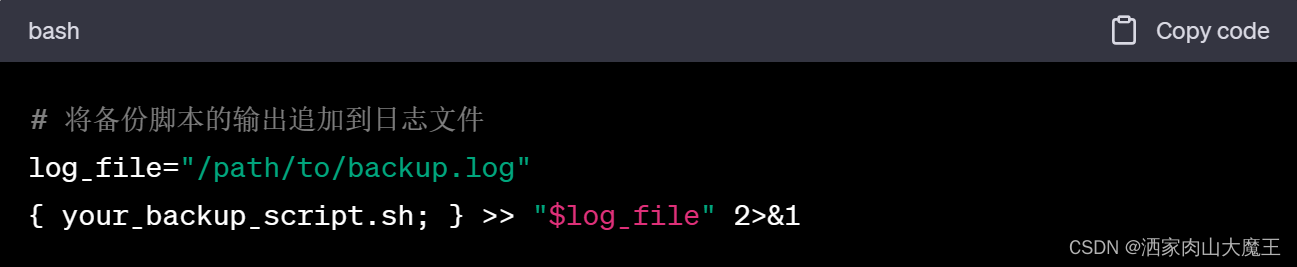
一个Linux自动备份脚本的示例
一个简单的Linux自动备份脚本的示例,根据需要进行自定义: 请确保按照您的需求修改source_dir和backup_dir为要备份的源目录和备份目录的路径。此脚本使用tar命令创建一个以当前日期命名的压缩备份文件,并在备份完成后检查是否成功。此外&…...
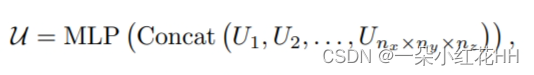
[论文阅读]PV-RCNN++
PV-RCNN PV-RCNN: Point-Voxel Feature Set Abstraction With Local Vector Representation for 3D Object Detection 论文网址:PV-RCNN 论文代码:PV-RCNN 简读论文 这篇论文提出了两个用于3D物体检测的新框架PV-RCNN和PV-RCNN,主要的贡献如下: 提出P…...
测试老鸟整理,Postman加密接口测试-Rsa/Aes对参数加密(详细总结)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 一些问题 postma…...

JavaScript使用对象
对象(object)是最基本、最通用的类型,具有复合性结构,属于引用型数据,对象的结构具有弹性,内部的数据是无序的,每个成员被称为属性。在JavaScript中,对象是一个泛化的概念,任何值都可以转换为对…...
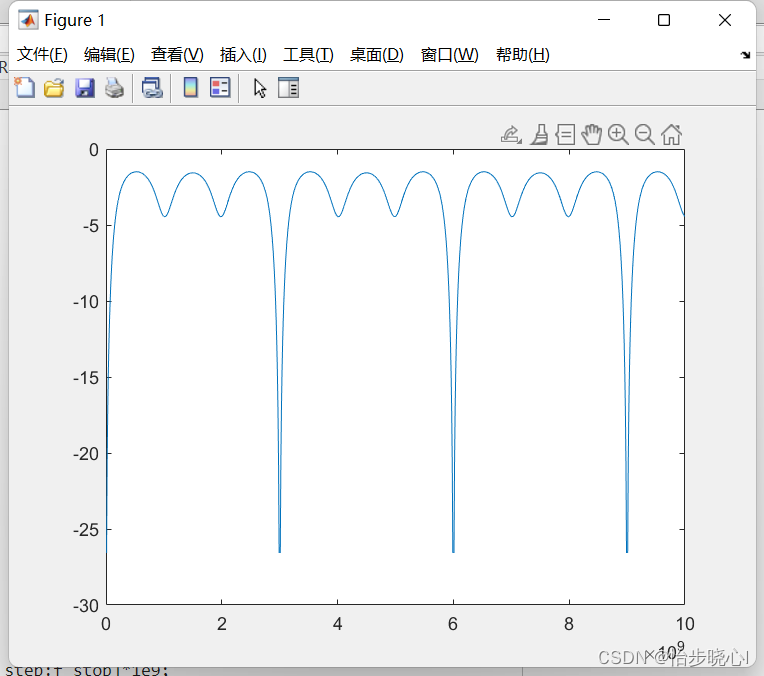
微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例
微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例 散射参数矩阵有实际的物理意义,但是其无法级联计算,但是ABCD参数和传输散射矩阵可以级联计算,在此先简单介绍ABCD参数矩阵的基本用法。 1、微带线的ABCD矩阵的推导 其他的一些常用的二端…...
“网站不安全”该如何解决
当我们的网站被客户访问的时候,经常会出现提示不安全的情况,导致客户的不信任,从而出现客户流失的现象,这种情况我们应该如何解决呢? 首先,我们要确定网站会出现不安全的原因,一般来说ÿ…...

gitlab数据备份和恢复
gitlab数据备份 sudo gitlab-rake gitlab:backup:create备份文件默认存放在/var/opt/gitlab/backups路径下, 生成1697101003_2023_10_12_12.0.3-ee_gitlab_backup.tar 文件 gitlab数据恢复 sudo gitlab-rake gitlab:backup:restore BACKUP1697101003_2023_10_12_…...
嵌入式Linux和stm32区别? 之间有什么关系吗?
嵌入式Linux和stm32区别? 之间有什么关系吗? 主要体现在以下几个方面: 1.硬件资源不同 单片机一般是芯片内部集成flash、ram,ARM一般是CPU,配合外部的flash、ram、sd卡存储器使用。最近很多小伙伴找我,说想要一些嵌…...

【Redis】String字符串类型-内部编码使用场景
文章目录 内部编码使用场景缓存功能计数功能共享会话手机验证码 内部编码 字符串类型的内部编码有3种: int:8个字节(64位)的⻓整型,存储整数embstr:压缩字符串,适用于表示较短的字符串raw&…...

电脑发热发烫,具体硬件温度达到多少度才算异常?
环境: 联想E14 问题描述: 电脑发热发烫,具体硬件温度达到多少度才算异常? 解决方案: 电脑硬件的温度正常范围会因设备类型和使用的具体硬件而有所不同。一般来说,以下是各种硬件的正常温度范围: CPU:正…...

计算机网络第4章-IPv6和寻址
IP地址的分配 为了获取一块IP地址用于一个组织的子网内,于是我们向ISP联系,ISP则会从已分给我们的更大 地址块中提供一些地址。 例如,ISP也许已经分配了地址块200.23.16.0/20。 该ISP可以依次将该地址块分成8个长度相等的连续地址块&…...
Lazarus安装和入门资料
azarus-2.2.6-fpc-3.2.2-win64 下载地址 Lazarus 基础教程 - Lazarus Tutorials for Beginners Lazarus Tutorial #1 - Learning programming_哔哩哔哩_bilibili https://www.devstructor.com/index.php?pagetutorials Lazarus是一款开源免费的object pascal语言RAD IDE&…...

mediapipe流水线分析 二
目标检测 Graph 一 流水线上游输入处理 1 TfLiteConverterCalculator 将输入的数据转换成tensorflow api 支持的Tensor TfLiteTensor 并初始化相关输入输出节点 ,该类的业务主要通过 interpreter std::unique_ptrtflite::Interpreter interpreter_ nullptr; 实现…...
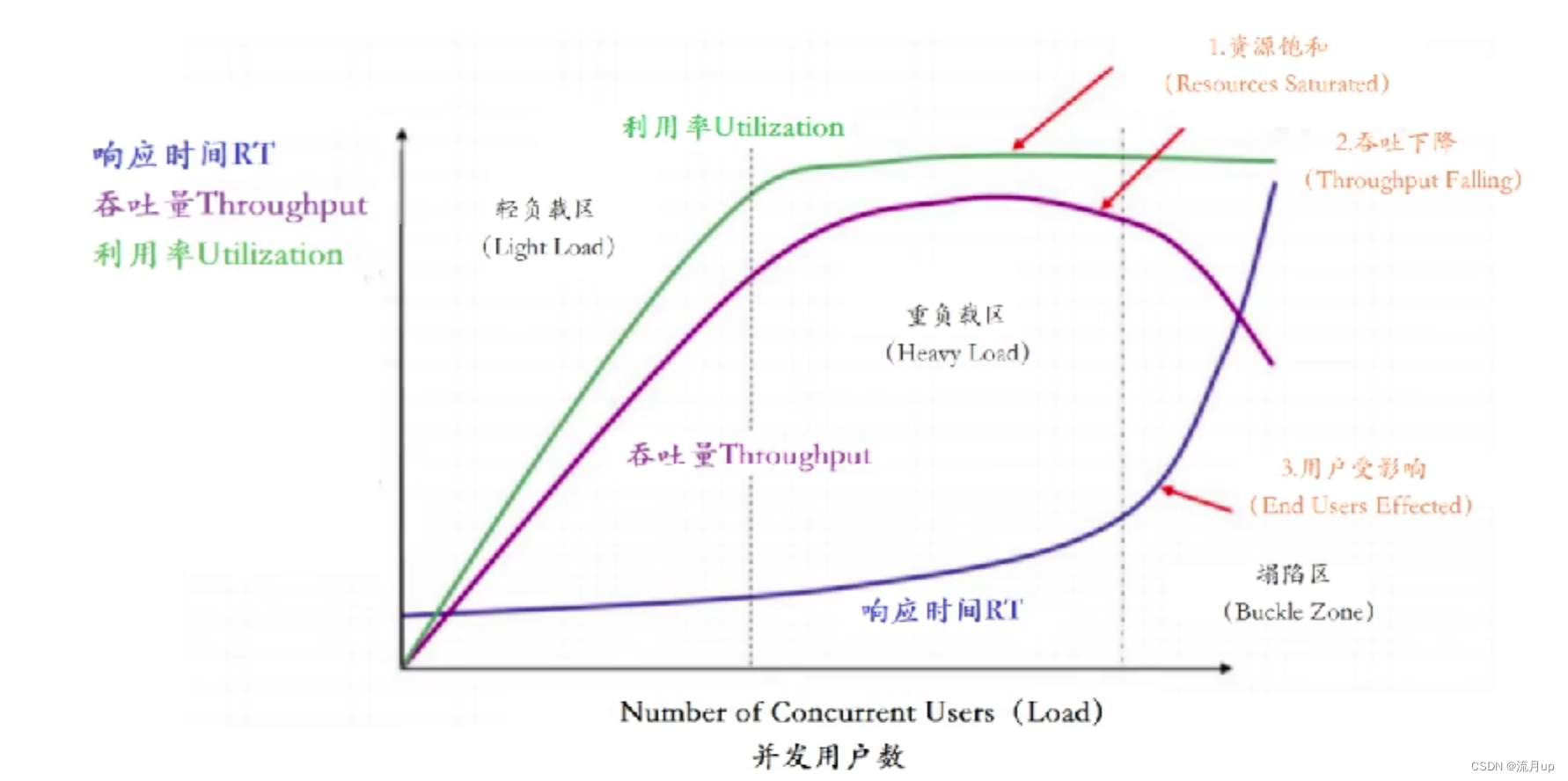
1.性能优化
概述 今日目标: 性能优化的终极目标是什么压力测试压力测试的指标 性能优化的终极目标是什么 用户体验 产品设计(非技术) 系统性能(快,3秒不能更久了) 后端:RT,TPS,并发数 影响因素01:数据库读写,RPCÿ…...
使用Plsql+oracle client 连接 Oracle数据库
2011年入职老东家X煤集团的时候,在csnd上写了一篇blog,题目叫“什么是ERP”,从此跳入DBA了这个烂坑,目前公司的数据库一部分是Oracle,另一部分是MySQL的,少量MSSQL,还需要捡起来一部分ÿ…...
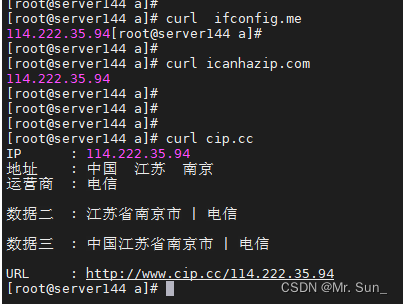
centos获取服务器公网ip
查看公网IP 用下面几个命令: #curl ifconfig.me #curl icanhazip.com #curl cip.cc...

思谋科技进博首秀:工业多模态大模型IndustryGPT V1.0正式发布
大模型技术正在引领新一轮工业革命,但将其应用于工业制造,仍面临许多挑战,专业知识的缺乏是关键难点。11月5日,香港中文大学终身教授、思谋科技创始人兼董事长贾佳亚受邀参加第六届中国国际进口博览会暨虹桥国际经济论坛开幕式。虹…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
