力扣第300题 最长递增子序列 c++ 动态规划题 附Java代码
题目
300. 最长递增子序列
中等
相关标签
数组 二分查找 动态规划
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
进阶:
- 你能将算法的时间复杂度降低到
O(n log(n))吗?
思路和解题方法
if(nums.size()<=1) return nums.size();:特判,如果数组nums长度为0或1,直接返回其长度。vector<int> dp(nums.size(), 1);:创建一个大小为nums长度的数组dp,用于存储以nums[i]结尾的最长上升子序列的长度。初始值全部赋为1,因为每个元素本身也可以构成一个长度为1的上升子序列。int ans = 0;:初始化最长上升子序列的长度为0。for(int i = 1; i < nums.size(); i++):从第二个元素开始遍历数组nums。for(int j = 0; j < i; j++):在i之前的元素中,找到比nums[i]小的元素。if(nums[i] > nums[j]):如果nums[i]大于nums[j],则可以将nums[i]加入到以nums[j]结尾的最长上升子序列中。dp[i] = max(dp[i], dp[j] + 1);:更新以nums[i]结尾的最长上升子序列的长度。当前位置的值为前面比它小的元素中以每个元素结尾的最长上升子序列长度的最大值+1。if(ans < dp[i]) ans = dp[i];:更新最长上升子序列的长度。return ans;:返回最长上升子序列的长度。
复杂度
时间复杂度:
O(n*n)
时间复杂度分析: 代码中使用了两重循环,时间复杂度为O(n^2)。
其中,内层循环每次迭代都会执行常数个操作(比较和更新dp数组),因此时间复杂度为O(1)。
外层循环的迭代次数为n-1,因此时间复杂度为O(n)。
因此,算法的总时间复杂度为O(n^2)。
空间复杂度
O(n)
空间复杂度分析: 代码中使用了一个长度为n的dp数组,因此空间复杂度为O(n)。
c++ 代码
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if(nums.size()<=1) return nums.size();vector<int> dp(nums.size(), 1); // 创建一个dp数组,用于存储以nums[i]结尾的最长上升子序列的长度,默认初始为1int ans = 0; // 初始化最长上升子序列的长度为0for(int i = 1; i < nums.size(); i++) // 遍历数组nums{for(int j = 0; j < i; j++) // 在i之前的元素中,找到比nums[i]小的元素{if(nums[i] > nums[j]) // 如果nums[i]大于nums[j],则可以将nums[i]加入到以nums[j]结尾的最长上升子序列中dp[i] = max(dp[i], dp[j] + 1); // 更新以nums[i]结尾的最长上升子序列的长度}if(ans < dp[i]) // 更新最长上升子序列的长度ans = dp[i];}return ans; // 返回最长上升子序列的长度}
};Java代码
class Solution {public int lengthOfLIS(int[] nums) {int[] dp = new int[nums.length]; // 创建一个大小为nums.length的数组dp,用于存储以nums[i]结尾的最长上升子序列的长度,默认初始为1int res = 0; // 初始化最长上升子序列的长度为0Arrays.fill(dp, 1); // 将dp数组中的元素全部赋值为1for (int i = 1; i < dp.length; i++) { // 遍历数组nums,从第二个元素开始for (int j = 0; j < i; j++) { // 在i之前的元素中,找到比nums[i]小的元素if (nums[i] > nums[j]) { // 如果nums[i]大于nums[j],则可以将nums[i]加入到以nums[j]结尾的最长上升子序列中dp[i] = Math.max(dp[i], dp[j] + 1); // 更新以nums[i]结尾的最长上升子序列的长度}res = Math.max(res, dp[i]); // 更新最长上升子序列的长度}}return res; // 返回最长上升子序列的长度}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第300题 最长递增子序列 c++ 动态规划题 附Java代码
题目 300. 最长递增子序列 中等 相关标签 数组 二分查找 动态规划 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例…...

Si3262 集成低功耗SOC 三合一智能门锁应用芯片
Si3262 是一款G度集成的低功耗 SOC 芯片,其集成了基于 RISC-V 核的低功耗MCU 和工作在 13.56MHz 的非接触式读写器模块。 读写器模块支持 ISO/IEC 14443 A/B/MIFARE 协议,支持自动载波侦测功能(ACD)。无需外W其他电路,…...
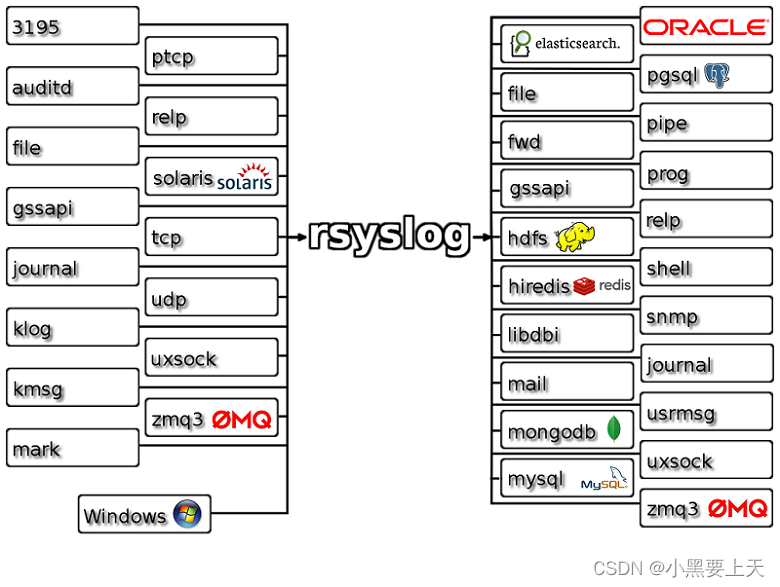
linux rsyslog介绍
Rsyslog网址:https://www.rsyslog.com/ Rsyslog is the rocket-fast system for log processing. It offers high-performance, great security features and a modular design. While it started as a regular syslogd, rsyslog has evolved into a kind of swis…...

项目部署之安装和配置Canal
1.Canal介绍 Canal是阿里巴巴的一个开源项目,基于java实现,整体已经在很多大型的互联网项目生产环境中使用,包括阿里、美团等都有广泛的应用,是一个非常成熟的数据库同步方案,基础的使用只需要进行简单的配置即可。 …...

基于Skywalking的全链路跟踪实现
在前文“分布式应用全链路跟踪实现”中介绍了分布式应用全链路跟踪的几种实现方法,本文将重点介绍基于Skywalking的全链路实现,包括Skywalking的整体架构和基本概念原理、Skywalking环境部署、SpringBoot和Python集成Skywalking监控实现等。 1、Skywalki…...

Spark Core
Spark Core 本文来自 B站 黑马程序员 - Spark教程 :原地址 第一章 RDD详解 1.1 为什么需要RDD 分布式计算需要 分区控制shuffle控制数据存储、序列化、发送数据计算API等一系列功能 这些功能,不能简单的通过Python内置的本地集合对象(如…...
)
[算法日志]图论: 广度优先搜索(BFS)
[算法日志]图论: 广度优先搜索(BFS) 广度优先概论 广度优先遍历也是一种常用的遍历图的算法策略,其思想是将本节点相关联的节点都遍历一遍后才切换到相关联节点重复本操作。这种遍历方式类似于对二叉树节点的层序遍历,即先遍历完子节点后…...
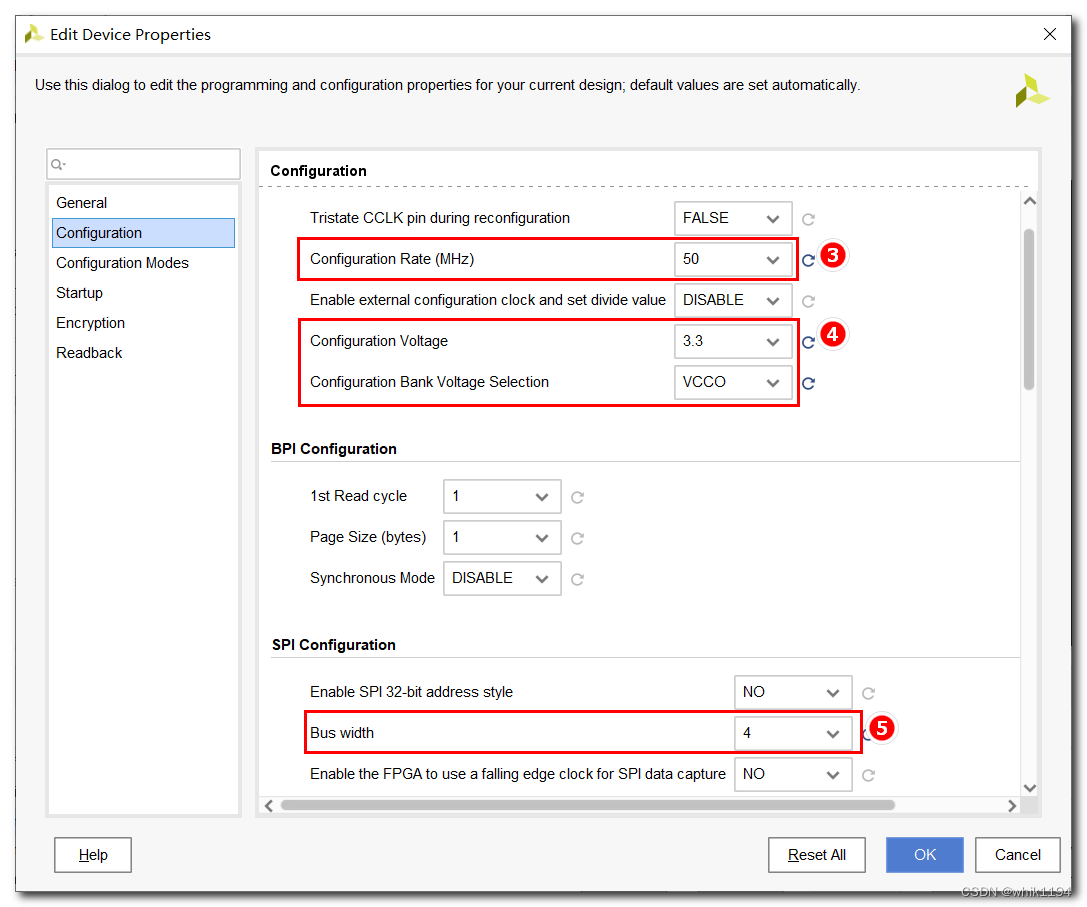
Xilinx FPGA SPIx4 配置速度50M约束语句(Vivado开发环境)
qspi_50m.xdc文件: set_property BITSTREAM.GENERAL.COMPRESS TRUE [current_design] set_property BITSTREAM.CONFIG.SPI_BUSWIDTH 4 [current_design] set_property BITSTREAM.CONFIG.CONFIGRATE 50 [current_design] set_property CONFIG_VOLTAGE 3.3 [curren…...

Linux Shell和权限
目录 Shell命令及运行原理 权限 1.文件基本属性 2.文件权限值的表示方法 3.文件访问权限的相关设置方法 3.(1)chmod 组名修改 3.(2)chmod 二进制修改 3.(3)chown 3.(4)chgrp 3.(5)umask 4.目录权限 Shell命令及运行原理 Linux的操作系统,狭义上是…...
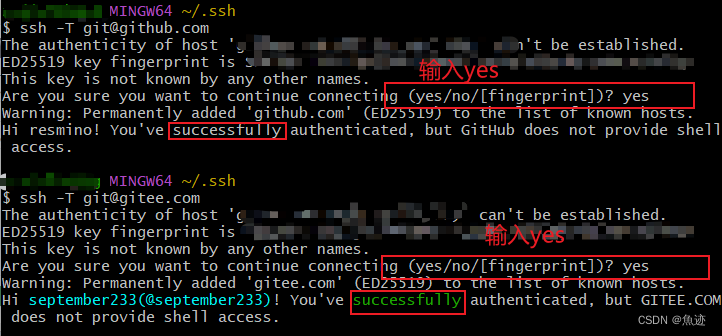
Git同时配置Gitee和GitHub
Git同时配置Gitee和GitHub 一、删除原先ssh密钥二、生成密钥 这里的同时配置是针对于之前配置过单个gitee或者github而言的,如果需要看git从安装开始的配置,则可以看这一篇文章 git安装配置教程 一、删除原先ssh密钥 在C盘下用户/用户名/.ssh文件下找到…...

IGP高级特性简要介绍(OSPF-上篇)
OSPF高级特性 一、OSPF_提升故障收敛及网络恢复速度 1.FRR与BFD快速恢复故障 1.1 FRR 在传统转发模式下,当到达同一个目的网络存在多条路由时,路由器总是选择最优路由使用,并且下发到FIB表指导数据转发。 当最优路由故障时,需…...

Oracle-Ogg集成模式降级为经典模式步骤
前言: Ogg集成模式降级为经典模式的场景比较少,因为降级为经典模式会导致无法支持压缩表同步,XA事务,多线程模式,PDB模式同步等功能,除非遇到集成模式暂时无法解决的bug或者环境不支持集成模式,比如DG备库环…...
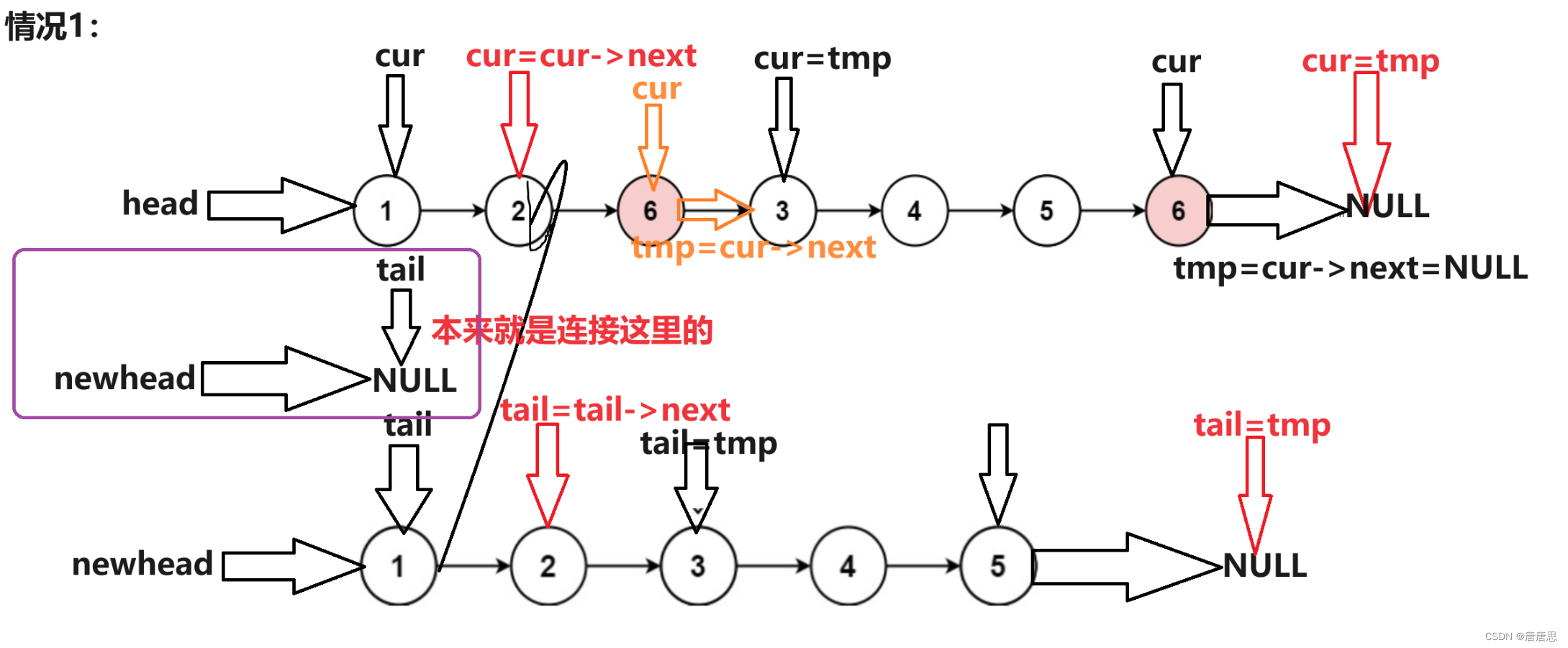
链表面试OJ题(1)
今天讲解两道链表OJ题目。 1.链表的中间节点 给你单链表的头结点 head ,请你找出并返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。 示例 输入:head [1,2,3,4,5] 输出:[3,4,5] 解释:链表只有一个…...
[极客大挑战 2019]Upload 1
题目环境: 根据题目和环境可知此题目是一道文件上传漏洞 编写一句话木马脚本<?php eval($_POST[shell]);?>将脚本文件更改为jpg图片文件我这里是flag.jpg上传文件并burpsuite抓包Repeater重放 报错一句话木马里面有<?字符 换一种一句话木马继续编写木马…...

OpenFeign讲解+面试题
一:OpenFeign是什么? 是一个声明式的web客户端,只需要创建一个接口,添加注解即可完成微服务之间的调用 二:调用微服务的方式? ribbon restTemplate方式调用openFeign通过接口注解的方式调用 三:如何使用OpenFeign&…...

嬴图 | LLM+Graph:大语言模型与图数据库技术的协同
前言 2022年11月以来,大语言模型席卷全球,在自然语言任务中表现卓越。尽管存在一系列伦理、安全等方面的担心,但各界对该技术的热情和关注并未减弱。 本文不谈智能伦理方面的问题,仅集中于Ulitpa嬴图在应用中的一些探索与实践&a…...

微信小程序下载文件和转发文件给好友总结
这段时间公司让我负责小程序的一些功能开发,回想上次开发小程序还是在上一次,这次开发小程序主要实现的功能就是转发文件给好友和下载文件,总结一下这次遇到的各种问题和解决方法。 下载文件 首先正常下载 wx.downloadFile({url: https://img.haihaina.cn/月度支出表.xls,…...
一文掌握 Apache SkyWalking
Apache SkyWalking SkyWalking是一个开源可观测平台,用于收集、分析、聚合和可视化来自服务和云原生基础设施的数据。SkyWalking 提供了一种简单的方法来保持分布式系统的清晰视图,甚至跨云。它是一种现代APM,专为云原生、基于容器的分布式系…...

外贸网站优化常用流程和一些常识
外贸网站google排名,总以为是单个网页标签的优化过程。 显然,这些观点都是错误的,九凌网络是做谷歌优化服务,九凌网络跟大家分享外贸网站Google优化常用流程和一些常识需要做以下几个步骤: 第一步:网站诊断࿰…...

Hive的时间操作函数
目录 前言函数使用介绍实际使用判断该天是星期几判断该天对应的周(包含一周开始和结束) 前言 hive 里面的时间函数有很多,今天单讲dayofweek函数,背景:有时候不仅要出日报,还要出周报,需要很多…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...

codeforces C. Cool Partition
目录 题目简述: 思路: 总代码: https://codeforces.com/contest/2117/problem/C 题目简述: 给定一个整数数组,现要求你对数组进行分割,但需满足条件:前一个子数组中的值必须在后一个子数组中…...
