3 决策树及Python实现
1 主要思想
1.1 数据
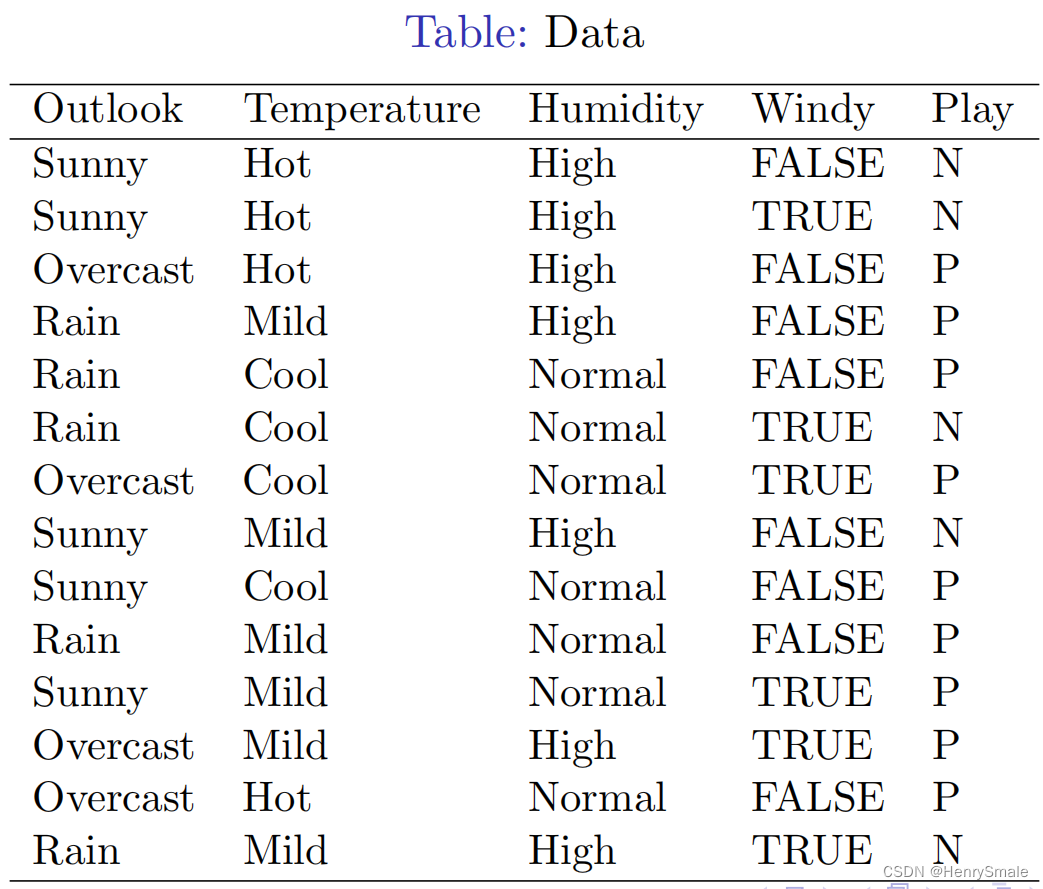
1.2 训练和使用模型
训练:建立模型(树)
测试:使用模型(树)
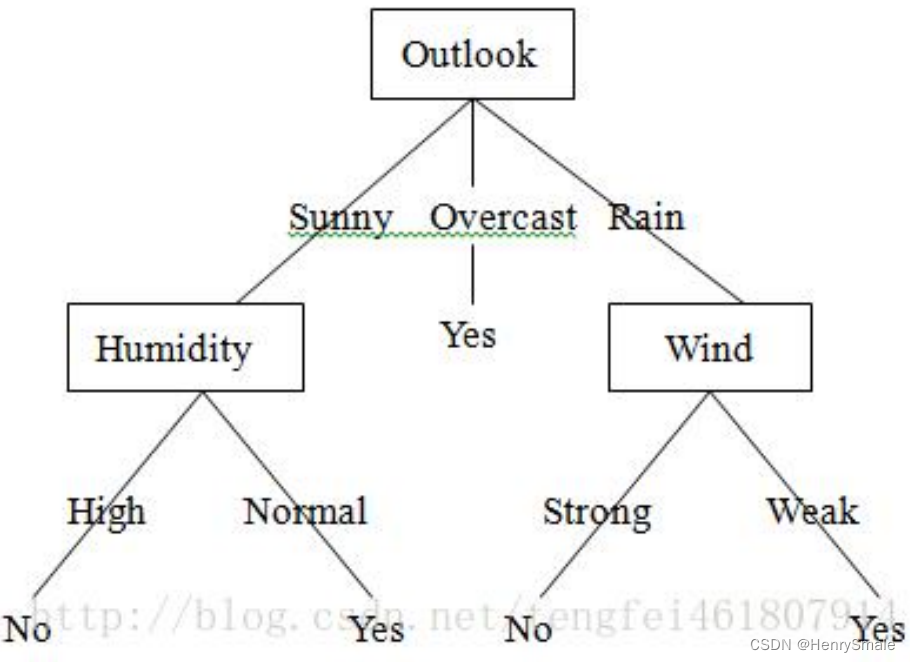
Weka演示ID3(终端用户模式)
- 双击weka.jar
- 选择Explorer
- 载入weather.arff
- 选择trees–>ID3
- 构建树,观察结果
建立决策树流程
- Step 1. 选择一个属性
- Step 2. 将数据集分成若干子集
- Step 3.1 对于决策属性值唯一的子集, 构建叶结点
- Step 3.2 对于决策属性值不唯一的子集, 递归调用本函数
演示: 利用txt文件, 按照决策树的属性划分数据集
2 信息熵
问题: 使用哪个属性进行数据的划分?
随机变量YYY的信息熵为 (YYY为决策变量):
H(Y)=E[I(yi)]=∑i=1np(yi)log1p(yi)=−∑i=1np(yi)logp(yi),H(Y) = E[I(y_i)] = \sum_{i=1}^n p(y_i)\log \frac{1}{p(y_i)} = - \sum_{i=1}^n p(y_i)\log p(y_i), H(Y)=E[I(yi)]=i=1∑np(yi)logp(yi)1=−i=1∑np(yi)logp(yi),
其中 0log0=00 \log 0 = 00log0=0.
随机变量YYY关于XXX的条件信息熵为(XXX为条件变量):
H(Y∣X)=∑i=1mp(xi)H(Y∣X=xi)=−∑i,jp(xi,yj)logp(yj∣xi).\begin{array}{ll} H(Y | X) & = \sum_{i=1}^m p(x_i) H(Y | X = x_i)\\ & = - \sum_{i, j} p(x_i, y_j) \log p(y_j | x_i). \end{array} H(Y∣X)=∑i=1mp(xi)H(Y∣X=xi)=−∑i,jp(xi,yj)logp(yj∣xi).
XXX为YYY带来的信息增益: H(Y)−H(Y∣X)H(Y) - H(Y | X)H(Y)−H(Y∣X).
3 程序分析
版本1. 使用sklearn (调包侠)
这里使用了数据集是数值型。
import numpy as np
import scipy as sp
import time, sklearn, math
from sklearn.model_selection import train_test_split
import sklearn.datasets, sklearn.neighbors, sklearn.tree, sklearn.metricsdef sklearnDecisionTreeTest():#Step 1. Load the datasettempDataset = sklearn.datasets.load_breast_cancer()x = tempDataset.datay = tempDataset.target# Split for training and testingx_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2)#Step 2. Build classifiertempClassifier = sklearn.tree.DecisionTreeClassifier(criterion='entropy')tempClassifier.fit(x_train, y_train)#Step 3. Test#precision, recall, thresholds = sklearn.metrics.precision_recall_curve(y_test, tempClassifier.predict(x_test))tempAccuracy = sklearn.metrics.accuracy_score(y_test, tempClassifier.predict(x_test))tempRecall = sklearn.metrics.recall_score(y_test, tempClassifier.predict(x_test))#Step 4. Outputprint("precision = {}, recall = {}".format(tempAccuracy, tempRecall))sklearnDecisionTreeTest()
版本2. 自己重写重要函数
- 信息熵
#计算给定数据集的香农熵
def calcShannonEnt(paraDataSet):numInstances = len(paraDataSet)labelCounts = {} #定义空字典for featVec in paraDataSet:currentLabel = featVec[-1]if currentLabel not in labelCounts.keys():labelCounts[currentLabel] = 0labelCounts[currentLabel] += 1shannonEnt = 0.0for key in labelCounts:prob = float(labelCounts[key])/numInstancesshannonEnt -= prob * math.log(prob, 2) #以2为底return shannonEnt
- 划分数据集
#dataSet 是数据集,axis是第几个特征,value是该特征的取值。
def splitDataSet(dataSet, axis, value):resultDataSet = []for featVec in dataSet:if featVec[axis] == value:#当前属性不需要reducedFeatVec = featVec[:axis]reducedFeatVec.extend(featVec[axis+1:])resultDataSet.append(reducedFeatVec)return resultDataSet
- 选择最好的特征划分
#该函数是将数据集中第axis个特征的值为value的数据提取出来。
#选择最好的特征划分
def chooseBestFeatureToSplit(dataSet):#决策属性不算numFeatures = len(dataSet[0]) - 1baseEntropy = calcShannonEnt(dataSet)bestInfoGain = 0.0bestFeature = -1for i in range(numFeatures):#把第i列属性的值取出来生成一维数组featList = [example[i] for example in dataSet]#剔除重复值uniqueVals = set(featList)newEntropy = 0.0for value in uniqueVals:subDataSet = splitDataSet(dataSet, i, value)prob = len(subDataSet) / float(len(dataSet))newEntropy += prob*calcShannonEnt(subDataSet)infoGain = baseEntropy - newEntropyif(infoGain > bestInfoGain):bestInfoGain = infoGainbestFeature = ireturn bestFeature
- 构建叶节点
#如果剩下的数据中无特征,则直接按最大百分比形成叶节点
def majorityCnt(classList):classCount = {}for vote in classList:if vote not in classCount.keys():classCount[vote] = 0classCount += 1;sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgette(1), reverse = True)return sortedClassCount[0][0]
- 创建决策树
#创建决策树
def createTree(dataSet, paraFeatureName):featureName = paraFeatureName.copy()classList = [example[-1] for example in dataSet]#Already pureif classList.count(classList[0]) == len(classList):return classList[0]#No more attributeif len(dataSet[0]) == 1:#if len(dataSet) == 1:return majorityCnt(classList)bestFeat = chooseBestFeatureToSplit(dataSet)#print(dataSet)#print("bestFeat:", bestFeat)bestFeatureName = featureName[bestFeat]myTree = {bestFeatureName:{}}del(featureName[bestFeat])featvalue = [example[bestFeat] for example in dataSet]uniqueVals = set(featvalue)for value in uniqueVals:subfeatureName = featureName[:]myTree[bestFeatureName][value] = createTree(splitDataSet(dataSet, bestFeat, value), subfeatureName)return myTree
- 分类和返回预测结果
#Classify and return the precision
def id3Classify(paraTree, paraTestingSet, featureNames, classValues):tempCorrect = 0.0tempTotal = len(paraTestingSet)tempPrediction = classValues[0]for featureVector in paraTestingSet:print("Instance: ", featureVector)tempTree = paraTreewhile True:for feature in featureNames:try:tempTree[feature]splitFeature = featurebreakexcept:i = 1 #Do nothingattributeValue = featureVector[featureNames.index(splitFeature)]print(splitFeature, " = ", attributeValue)tempPrediction = tempTree[splitFeature][attributeValue]if tempPrediction in classValues:breakelse:tempTree = tempPredictionprint("Prediction = ", tempPrediction)if featureVector[-1] == tempPrediction:tempCorrect += 1return tempCorrect/tempTotal
- 构建测试代码
def mfID3Test():#Step 1. Load the datasetweatherData = [['Sunny','Hot','High','FALSE','N'],['Sunny','Hot','High','TRUE','N'],['Overcast','Hot','High','FALSE','P'],['Rain','Mild','High','FALSE','P'],['Rain','Cool','Normal','FALSE','P'],['Rain','Cool','Normal','TRUE','N'],['Overcast','Cool','Normal','TRUE','P'],['Sunny','Mild','High','FALSE','N'],['Sunny','Cool','Normal','FALSE','P'],['Rain','Mild','Normal','FALSE','P'],['Sunny','Mild','Normal','TRUE','P'],['Overcast','Mild','High','TRUE','P'],['Overcast','Hot','Normal','FALSE','P'],['Rain','Mild','High','TRUE','N']]featureName = ['Outlook', 'Temperature', 'Humidity', 'Windy']classValues = ['P', 'N']tempTree = createTree(weatherData, featureName)print(tempTree)#print(createTree(mydata, featureName))#featureName = ['Outlook', 'Temperature', 'Humidity', 'Windy']print("Before classification, feature names = ", featureName)tempAccuracy = id3Classify(tempTree, weatherData, featureName, classValues)print("The accuracy of ID3 classifier is {}".format(tempAccuracy))def main():sklearnDecisionTreeTest()mfID3Test()main()
4 讨论
符合人类思维的模型;
信息增益只是一种启发式信息;
与各个属性值“平行”的划分。
其它决策树:
- C4.5:处理数值型数据
- CART:使用gini指数
相关文章:

3 决策树及Python实现
1 主要思想 1.1 数据 1.2 训练和使用模型 训练:建立模型(树) 测试:使用模型(树) Weka演示ID3(终端用户模式) 双击weka.jar选择Explorer载入weather.arff选择trees–>ID3构建树…...
小程序和Vue+uniapp+unicloud培训课件
文章目录**一、什么是小程序****1.1** **小程序简介****1.2** **小程序的特点****1.3** **小程序的开发流程**个人小程序和企业小程序的区别1.4 小程序代码构成1.4.1 JSON 配置1.4.2 WXML 模板**数据绑定**逻辑语法条件逻辑列表渲染模板引用共同属性1.4.3 WXSS 样式1.4.4 JS 逻…...
C语言--指针进阶2
目录前言函数指针函数指针数组指向函数指针数组的指针回调函数前言 本篇文章我们将继续学习指针进阶的有关内容 函数指针 我们依然用类比的方法1来理解函数指针这一全新的概念,如图1 我们用一段代码来验证一下: int Add(int x, int y) {return xy;…...

【步进电机和 Arduino】
【步进电机和 Arduino】 前言1. 什么是步进电机及其工作原理?1.1 步进电机结构1.2 绕线方式1.3 通电方式2. 如何使用Arduino和A17步进驱动器控制NEMA4988步进电机2.1 A4988 和 Arduino 连接2.2 测量AB相2.3 A4988 限流3. 步进电机和 Arduino3.1 示例代码 13.2 示例代码 24. 使…...
【面试一:|和||、和区别】
相同点: ||和&&都是逻辑运算符,而|和&是位运算符。位运算符的优先级要比逻辑运算符的优先级高。 &和&&的区别 &和&&都可以用作逻辑与的运算符,表示逻辑与(and),当运…...

【一天一门编程语言】使用汇编语言实现斐波那契数列
文章目录使用汇编语言实现斐波那契数列一、什么是斐波那契数列二、如何用汇编语言实现斐波那契数列一、汇编语言概念1.1 什么是汇编语言1.2 汇编语言的特点二、汇编语言指令2.1 简单指令2.2 复杂指令汇编语言程序结构代码实例指令集常用指令指令代码实例使用汇编语言实现斐波那…...

RabbitMQ实现死信队列
目录死信队列是什么怎样实现一个死信队列说明实现过程导入依赖添加配置编写mq配置类添加业务队列的消费者添加死信队列的消费者添加消息发送者添加消息测试类测试死信队列的应用场景总结死信队列是什么 “死信”是RabbitMQ中的一种消息机制,当你在消费消息时&#…...

【Linux】安装Tomcat教程
目录 1.上传安装包 2.解压安装包 3.启动Tomcat 4.查看启动日志 5.查看进程 6.开放端口 7.停止Tomcat 1.上传安装包 使用FinalShell自带的上传工具将Tomcat的二进制发布包上传到Linux(与前面上传JDK安装包步骤 一致)。 2.解压安装包 将上传上来的安装包解压到指定目录…...

学习笔记之Vuex(五)
Vuex(五)Vuex一、什么是Vuex二、Vuex工作原理三、搭建Vuex环境四、求和案例分析4.1 求和案例——vue实现4.2 求和案例——vuex实现(五)Vuex 一、什么是Vuex 1.概念 在Vue中实现集中式状态(数据)管理的一…...
SSM知识快速复习
SSM知识快速复习SpringIOCDIIOC容器在Spring中的实现常用注解Autowired注解的原理AOP相关术语作用动态代理实现原理事务Transactional事务属性:只读事务属性:超时事务属性:回滚策略事务属性:事务隔离级别事务属性:事务…...
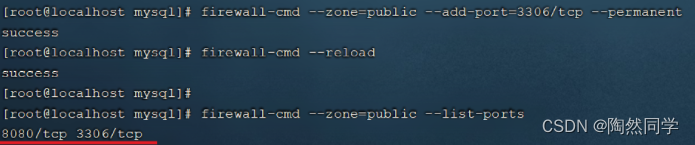
【Linux】安装MySQL
目录 1.检测当前系统是否安装过MySQL相关数据库 2. 卸载现有的MySQL数据库 3.上传解压 4.顺序安装rpm包 5.启动MySQL 6.查看临时密码 7.登录MySQL 8.开放端口 1.检测当前系统是否安装过MySQL相关数据库 需要通过rpm相关指令,来查询当前系统中是否存在已安…...
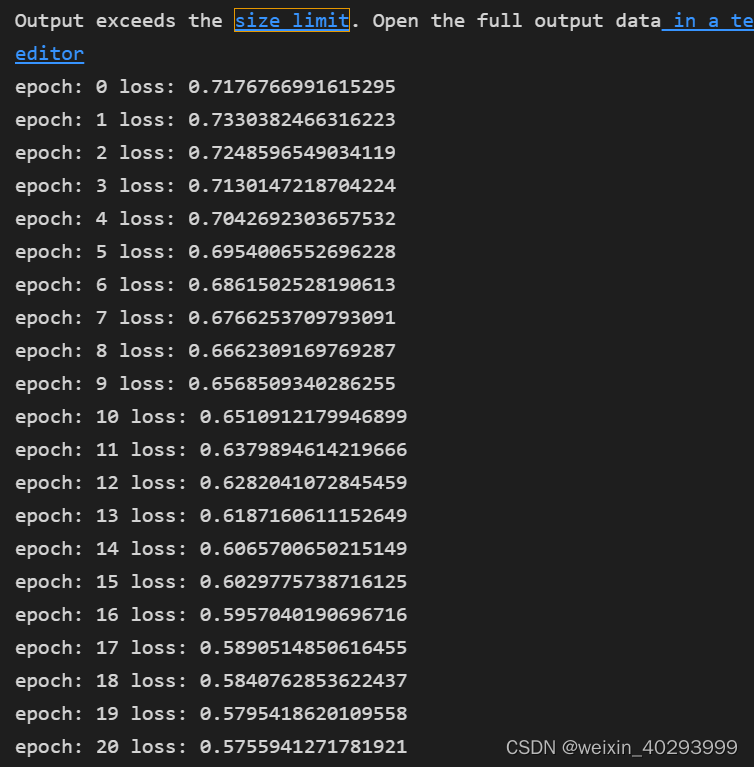
【深度学习】手把手教你开发自己的深度学习模板
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言1数据相关1.1 数据初探1.2.数据处理1.3 数据变形2 定义网络,优化函数3. 训练前言 入坑2年后,重新梳理之前的知识,发现其实需…...
一个诡异的 Pulsar InterruptedException 异常
背景 今天收到业务团队反馈线上有个应用往 Pulsar 中发送消息失败了,经过日志查看得知是发送消息时候抛出了 java.lang.InterruptedException 异常。 和业务沟通后得知是在一个 gRPC 接口中触发的消息发送,大约持续了半个小时的异常后便恢复正常了&…...
Java岗面试题--Java并发(volatile 专题)
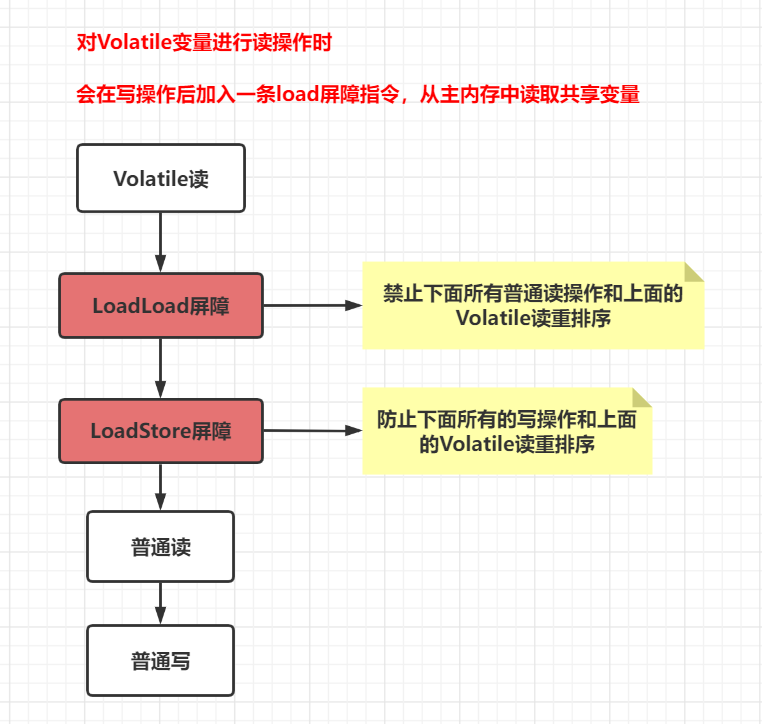
目录1. 面试题一:谈谈 volatile 的使用及其原理补充:内存屏障volatile 的原理2. 面试题二:volatile 为什么不能保证原子性3. 面试题三:volatile 的内存语义4. 面试题四:volatile 的实现机制5. 面试题五:vol…...
Java---打家劫舍ⅠⅡ
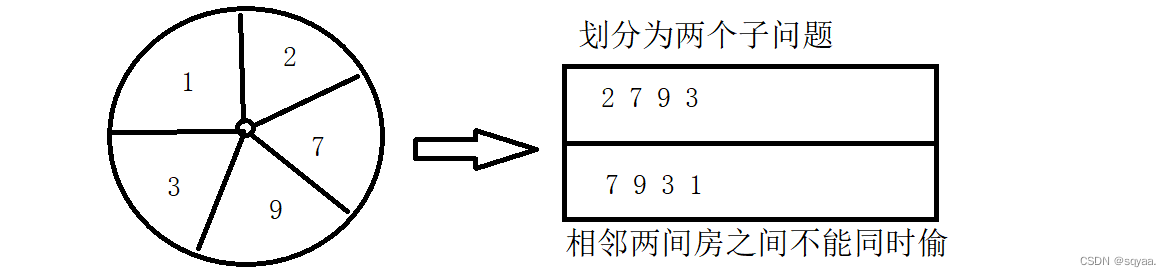
目录 打家劫舍Ⅰ 题目分析 代码一 代码二 打家劫舍Ⅱ 打家劫舍Ⅰ 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被…...

MySQL Lesson4
1:关于查询结果集的去重(distinct) select distinct job from emp; **distinct只能出现在所有字段的最前面。所表示的含有是所有的结果联合起来去重。 select distinct deptno,job from emp order by deptno; select count(distinct job)from…...

浅谈权限获取方法之文件上传
概述 文件上传漏洞是发生在有上传功能的应用中,如果应用程序对用户的上传文件没有控制或者存在缺陷,攻击者可以利用应用上传功能存在的缺陷,上传木马、病毒等有危害的文件到服务器上面,控制服务器。 漏洞成因及危害 文件上传漏…...
资产设备防拆标签安全防护和资产定位解决方案
随着社会经济的发展和高新技术的日新月异,对各方面的安全要求也在不断地提高,以物联网安防、入侵报警和出入口控制、应急系统等为主的安全防范系统日益成为各类文物场所智能化弱电工程不可或缺的组成部分,是重点资产管理场所内加强管理和安全…...
企业电子招标采购源码之电子招标投标全流程!
随着各级政府部门的大力推进,以及国内互联网的建设,电子招投标已经逐渐成为国内主流的招标投标方式,但是依然有很多人对电子招投标的流程不够了解,在具体操作上存在困难。虽然各个交易平台的招标投标在线操作会略有不同࿰…...

【考研408】计算机网络笔记
文章目录计算机网络体系结构计算机网络概述计算机网络的组成计算机网络的功能计算机网络的分类计算机网络的性能指标课后习题计算机网络体系结构与参考模型计算机网络协议、接口、服务的概念ISO/OSI参考模型和TCP/IP模型课后习题物理层通信基础基本概念奈奎斯特定理与香农定理编…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
