【PAT甲级题解记录】1151 LCA in a Binary Tree (30 分)
【PAT甲级题解记录】1151 LCA in a Binary Tree (30 分)
前言
Problem:1151 LCA in a Binary Tree (30 分)
Tags:树的遍历 并查集 LCA
Difficulty:
剧情模式想流点汗想流点血死而无憾Address:1151 LCA in a Binary Tree (30 分)
问题描述
给定一棵二叉树,求两个元素 lowest common ancestor (LCA) 即最低公共祖先,也就是离两个元素的最近公共祖先节点。
解题思路
这道题至少可以有两种解法:
- 暴力并查集法:利用并查集,说是并查集,其实只是一个保存前置节点的数组,在建树的过程中就可以得到。然后对输入的元素分别向上遍历,找到第一个相同的即可,但节点的值可以为负数,若存储下标也会超范围,所以我们需要离散化,可以自己写离散化,也可以利用map直接写(实测这道题需要unorder_map才不会超时)。
- DFS建树法:结合建树过程(这种方法其实不用建树,但是与建树的递归逻辑重合),利用中序遍历数组的规律,当需要求的两个点分别在左右子树时则可确认当前分叉点就是LCA,否则就往两个点所在的子树dfs。可以参考柳:https://blog.csdn.net/liuchuo/article/details/82560863
排一个测试点2的坑,就是可能出现U=R的情况,此时应该输出U is an ancestor of V.
参考代码
- 暴力并查集法
/** @Author: Retr0.Wu* @Date: 2022-02-20 00:29:21* @Last Modified by: Retr0.Wu* @Last Modified time: 2022-02-21 20:56:14*/
#include <bits/stdc++.h>
#include <unordered_map> // 我的万能头不包含所以我加了
using namespace std;
int N, M;
vector<int> dep_v[10010]; // 每一层有哪些值
unordered_map<int, int> pre;
unordered_map<int, int> visit;
vector<int> in_order(10010);
vector<int> pre_order(10010);
int cnt;
vector<int> ansv;
vector<int> build(int prenumber, int in_l, int in_r, int pre_l, int pre_r)
{// 在in里找pre的第一个int pos = 0;for (int i = in_l; i <= in_r; i++){if (in_order[i] == pre_order[pre_l]){pos = i;break;}}pre[pre_order[pre_l]] = prenumber;// 左子树的大小 pos-in_lif (pos > in_l){// tree[2 * root + 1] = pre_order[pre_l + 1];vector<int> tv = build(pre_order[pre_l], in_l, pos - 1, pre_l + 1, pre_l + pos - in_l);}if (pos < in_r){// tree[2 * root + 2] = pre_order[pre_l + pos - in_l + 1];vector<int> tv = build(pre_order[pre_l], pos + 1, in_r, pre_l + pos - in_l + 1, pre_r);}return ansv;
}
int main()
{//cin >> M >> N;scanf("%d %d",&M,&N);for (int i = 0; i < N; i++){scanf("%d",&in_order[i]);}for (int i = 0; i < N; i++){scanf("%d",&pre_order[i]);}build(pre_order[0], 0, N - 1, 0, N - 1);for (int i = 0; i < M; i++){int U, V;cin >> U >> V;if (pre.count(U) == 0 && pre.count(V) == 0){printf("ERROR: %d and %d are not found.\n", U, V);}else if (pre.count(U) == 0){printf("ERROR: %d is not found.\n", U);}else if (pre.count(V) == 0){printf("ERROR: %d is not found.\n", V);}else{visit.clear(); // 每一次都是新的查找公共根,必须清空int m = U, n = V;int ans = 0;int flag = 1;// 俩个点分俩条路径往上遍历,找最近的共同遍历点while (m != pre[m]){visit[m] = 1;m = pre[m];}while(n!=pre[n]){if(visit[n]==1){ans = n;flag = 0;break;}n = pre[n];}if(flag) ans = m; // 如果最终都没有找到除树根外的最近共同祖先,ans就只有可能是树根了if (ans == U){printf("%d is an ancestor of %d.\n", U, V);}else if (ans == V){printf("%d is an ancestor of %d.\n", V, U);}else{printf("LCA of %d and %d is %d.\n", U, V, ans);}}}return 0;
}- DFS建树法
#include<iostream>
#include<vector>
#include<map>
#include<cstdio>using namespace std;
int M; // the number of pairs of nodes to be tested (1e3)
int N; // the number of keys in the binary tree (1e4)
vector<int> pre_order, in_order;
map<int, int> pos;
int U, V;
int pos_U, pos_V; // U、V 在inorder中的位置
void init() {cin >> M >> N;in_order.resize(N), pre_order.resize(N);for (int i = 0; i < N; ++i) {cin >> in_order[i];pos[in_order[i]] = i;}for (int i = 0; i < N; ++i) cin >> pre_order[i];
}void creat_tree(int in_l, int in_r, int pre_l, int pre_r) {// find root in in_orderint pos_in = pos[pre_order[pre_l]];// LCA is found or U/V is an ancestor of anotherif ((pos_V < pos_in && pos_U > pos_in) || (pos_V > pos_in && pos_U < pos_in)) {printf("LCA of %d and %d is %d.\n", U, V, in_order[pos_in]);} else if (pos_U == pos_in) {printf("%d is an ancestor of %d.\n", U, V);} else if (pos_V == pos_in) {printf("%d is an ancestor of %d.\n", V, U);} else { // continue searchif (pos_U < pos_in && in_l < pos_in) { // search leftcreat_tree(in_l, pos_in - 1, pre_l + 1, pre_l + (pos_in - in_l));}if (pos_U > pos_in && in_r > pos_in) { // search rightcreat_tree(pos_in + 1, in_r, pre_l + (pos_in - in_l) + 1, pre_r);}}
}void test() {cin >> U >> V;// U/V is not foundif (pos.count(U) == 0 || pos.count(V) == 0) {if (pos.count(V) != 0) {printf("ERROR: %d is not found.\n", U);} else if (pos.count(U) != 0) {printf("ERROR: %d is not found.\n", V);} else {printf("ERROR: %d and %d are not found.\n", U, V);}return;}// LCA is found or U/V is an ancestor of anotherpos_V = pos[V], pos_U = pos[U];creat_tree(0, N - 1, 0, N - 1);
}void solution_1151() {init();for (int i = 0; i < M; i++) {test();}
}int main() {solution_1151();return 0;
}
总结
如果想要map速度不够,可以试试unordered_map。还是不行再考虑自己写映射离散化。
相关文章:
)
【PAT甲级题解记录】1151 LCA in a Binary Tree (30 分)
【PAT甲级题解记录】1151 LCA in a Binary Tree (30 分) 前言 Problem:1151 LCA in a Binary Tree (30 分) Tags:树的遍历 并查集 LCA Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1151 LCA in a Binary Tree (30 分…...

Android 获取手机语言环境 区分简体和繁体,香港,澳门,台湾繁体
安卓和IOS 系统语言都是准守:ISO 639 ISO 代码表IOS:plus.os.language ios正常,安卓下简体和繁体语言,都是zh安卓获取系统语言方法:Locale.getDefault().language手机切换到繁体(台湾,香港&…...

一文搞懂Python时间序列
Python时间序列1. datetime模块1.1 datetime对象1.2 字符串和datatime的相互转换2. 时间序列基础3. 重采样及频率转换4. 时间序列可视化5. 窗口函数5.1 移动窗口函数5.2 指数加权函数5.3 二元移动窗口函数时间序列(Time Series)是一种重要的结构化数据形…...
GeoServer发布数据进阶
GeoServer发布数据进阶 GeoServer介绍 GeoServer是用于共享地理空间数据的开源服务器。 它专为交互操作性而设计,使用开放标准发布来自任何主要空间数据源的数据。 GeoServer实现了行业标准的 OGC 协议,例如网络要素服务 (WFS)…...
Docker离线部署
Docker离线部署 目录 1、需求说明 2、下载docker安装包 3、上传docker安装包 4、解压docker安装包 5、解压的docker文件夹全部移动至/usr/bin目录 6、将docker注册为系统服务 7、重启生效 8、设置开机自启 9、查看docker版本信息 1、需求说明 大部份公司为了服务安全…...
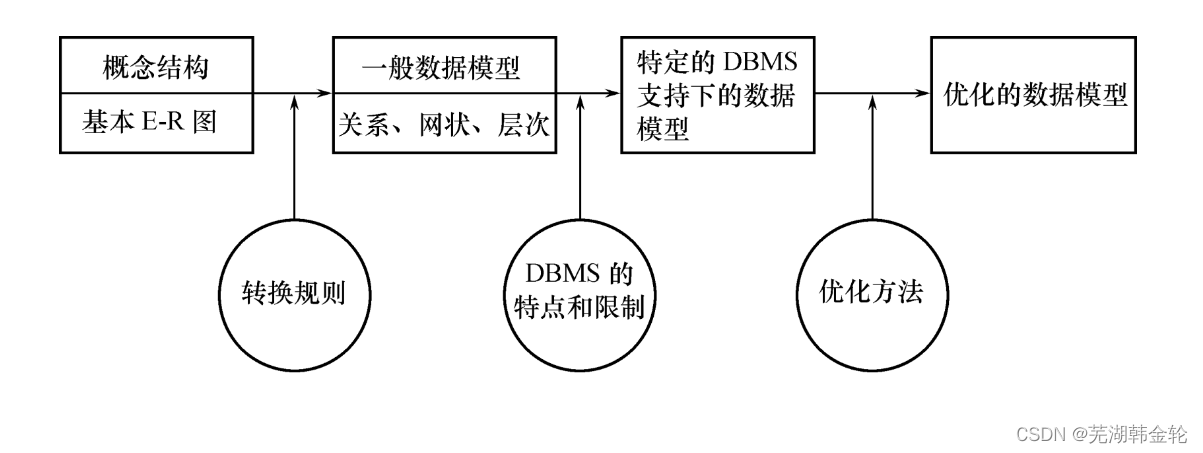
《数据库系统概论》学习笔记——第七章 数据库设计
教材为数据库系统概论第五版(王珊) 这一章概念比较多。最重点就是7.4节。 7.1 数据库设计概述 数据库设计定义: 数据库设计是指对于一个给定的应用环境,构造(设计)优化的数据库逻辑模式和物理结构&#x…...

【Datawhale图机器学习】半监督节点分类:标签传播和消息传递
半监督节点分类:标签传播和消息传递 半监督节点分类问题的常见解决方法: 特征工程图嵌入表示学习标签传播图神经网络 基于“物以类聚,人以群分”的Homophily假设,讲解了Label Propagation、Relational Classificationÿ…...
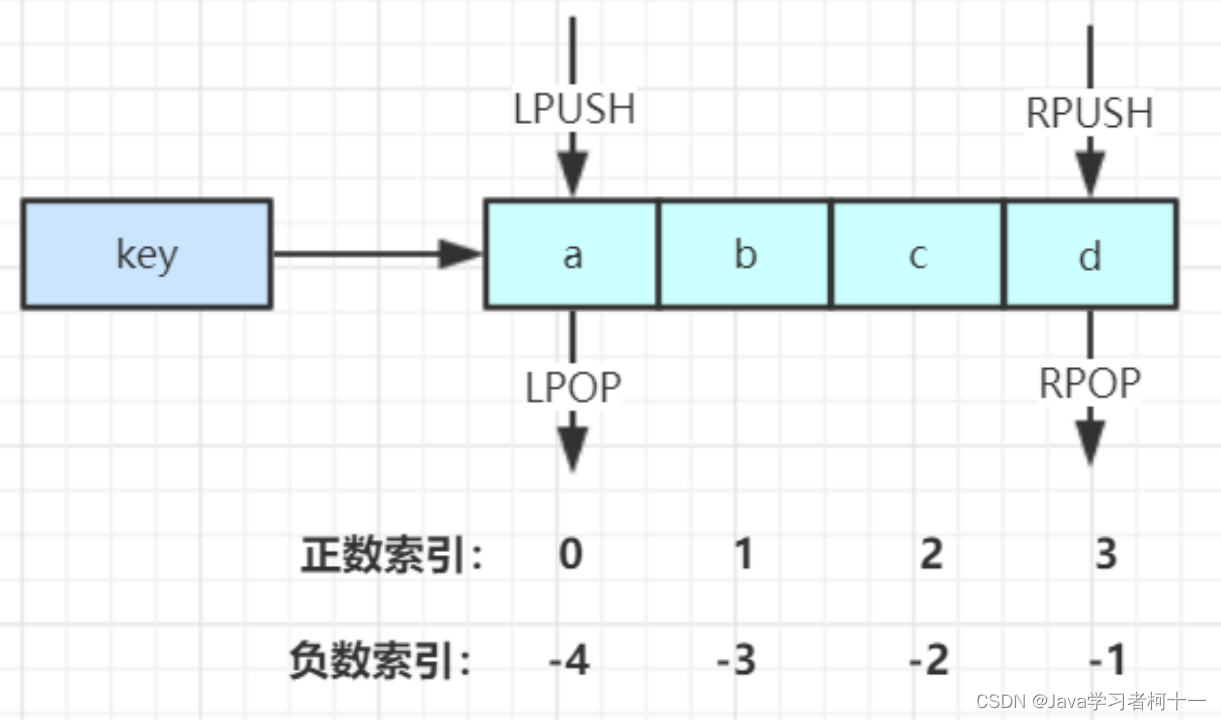
【分布式缓存学习篇】Redis数据结构
一、Redis的数据结构 二、String 数据结构 2.1 字符串常用操作 //存入字符串键值对 SET key value //批量存储字符串键值对 MSET key value [key value ...] //存入一个不存在的字符串键值对 SETNX key value //获取一个字符串键值 GET ke…...

【跟着ChatGPT学深度学习】ChatGPT带我入门NLP
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

RGB888与RGB565颜色
颜色名称RGB888原色RGB565还原色英RGB888[Hex]RGB888_R[Hex]RGB888_G[Hex]RGB888_B[Hex]RGB565[Hex]RGB565_R[Hex]RGB565_G[Hex]RGB565_B[Hex]黑色Black0x0000000000000x0000000昏灰Dimgray0x6969696969690x6B4DD1AD灰色Gray0x8080808080800x8410102010暗灰Dark Gray0xA9A9A9A9…...

常见的域名后缀有哪些?不同域名后缀的含义是什么?
域名发展至今,已演变出各种各样的域名后缀,导致很多网站管理人员在注册域名时不知该如何选择。下面,中科三方针对常见域名后缀种类,以及不同域名后缀的含义做下简单介绍。 什么是域名后缀? 域名是由一串由点分隔开的…...
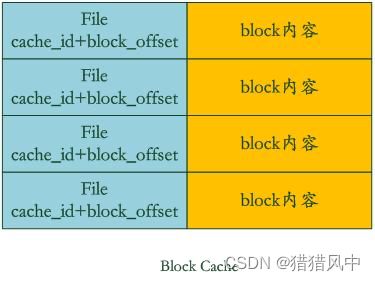
LevelDB架构介绍以及读、写和压缩流程
LevelDB 基本介绍 是一个key/value存储,key值根据用户指定的comparator排序。 特性 keys 和 values 是任意的字节数组。数据按 key 值排序存储。调用者可以提供一个自定义的比较函数来重写排序顺序。提供基本的 Put(key,value),Get(key),…...

华为OD机试模拟题 用 C++ 实现 - 快递货车(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明快递货车题目输入输出示例一输入输出Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单…...
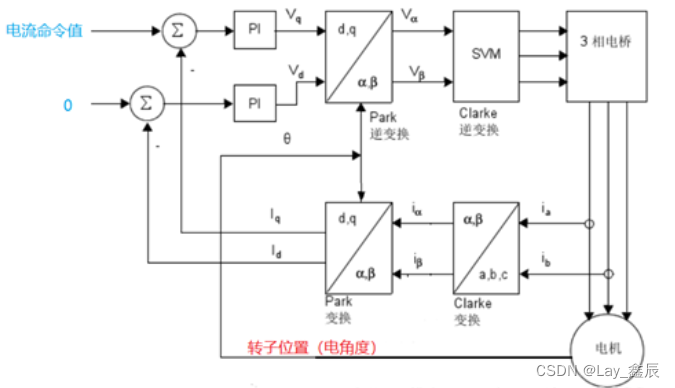
伺服三环控制深层原理解析
我们平时使用的工业伺服,通常是成套伺服,即驱动器和电机型号存在配对关系。 但有些时候,我们要用电机定转子和编码器制作非成套电机,这种时候,我们需要对驱动器进行各种设置才能驱动电机。 此篇文章将通过介绍伺服控制的三环控制原理入手来说明我们调试非成套伺服时需要…...
)
Cornerstone完整的基于 Web 的医学成像平台(一)
1.简介 Cornerstone是一个开源的基于Web的医学成像平台,它提供了一个易于使用的界面,可以用于加载、显示和处理医学图像。Cornerstone可以用于许多医学图像处理应用程序,例如计算机断层扫描(CT)、磁共振成像ÿ…...
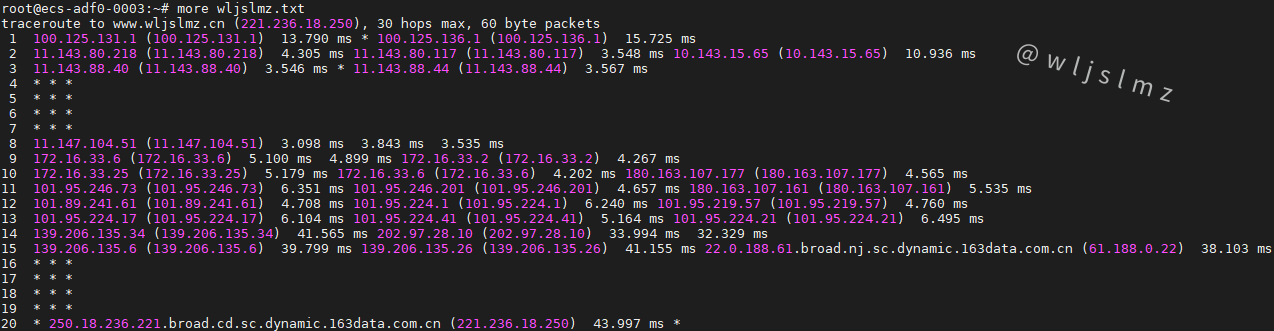
老板让我在Linux中使用traceroute排查服务器网络问题,幸好我收藏了这篇文章!
一、前言 作为网络工程师或者运维工程师,traceroute命令不会陌生,它的作用类似于ping命令,用于诊断网络的连通性,不过traceroute命令输出的命令会比ping命令丰富的多,可以跟踪从源系统到目标系统的路径。 很多工程师…...

一文读懂【数据埋点】
数据埋点是数据采集领域(尤其是用户行为数据采集领域)的术语,指的是针对特定用户行为或事件进行捕获、处理和发送的相关技术及其实施过程。比如用户某个icon点击次数、观看某个视频的时长等等。 数据分析是我们获得需求的来源之一,…...

Qt图片定时滚动播放器+透明过渡动画
目录参考结构PicturePlay.promain.cppmyqlabel.h 自定义QLabelmyqlabel.cpp自定义QLabelpictureplay.hpictureplay.cpppictureplay.uistyle.qss效果源码参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 Qt的动画类修改…...

手把手带你做一套毕业设计-征程开启
本文是《手把手带你做一套毕业设计》专栏的开篇,文本将会包含我们创作这个专栏的初衷,专栏的主体内容,以及我们专栏的后续规划。关于这套毕业设计的作者呢前端部分由狗哥负责,服务端部分则由天哥操刀。我们力求毕业生或者新手通过…...

万字解析 Linux 中 CPU 利用率是如何算出来的?
在线上服务器观察线上服务运行状态的时候,绝大多数人都是喜欢先用 top 命令看看当前系统的整体 cpu 利用率。例如,随手拿来的一台机器,top 命令显示的利用率信息如下 这个输出结果说简单也简单,说复杂也不是那么容易就能全部搞明白…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
