《数据库系统概论》学习笔记——第六章 关系数据理论
教材为数据库系统概论第五版(王珊)
这一章重点在于各种范式的概念和将低级范式转为高级范式。一定要看多值依赖和4NF(因为这个概念很绕又烦,但是期中期末都考了)。最后计算题就是一定要会:算闭包,求候选码,求最小函数依赖集,看本文的几题例题基本就会了。
6.1 问题的提出
关系数据库逻辑设计
- 针对具体问题,如何构造一个适合于它的数据模式
- 数据库逻辑设计的工具──关系数据库的规范化理论
一、概念回顾
- 关系
- 关系模式
- 关系数据库
- 关系数据库的模式
二、关系模式的形式化定义
关系模式由五部分组成,即它是一个五元组:
R(U, D, DOM, F)
- R: 关系名
- U: 组成该关系的属性名集合
- D: 属性组U中属性所来自的域
- DOM: 属性向域的映象集合
- F: 属性间数据的依赖关系集合
三、什么是数据依赖
1. 完整性约束的表现形式
- 限定属性取值范围:例如学生成绩必须在0-100之间
- 定义属性值间的相互关连(主要体现于值的相等与否),这就是数据依赖,它是数据库模式设计的关键
2. 数据依赖
- 一个关系内部属性与属性之间的约束关系
- 现实世界属性间相互联系的抽象
- 数据内在的性质
- 语义的体现
3. 数据依赖的类型
- 函数依赖(Functional Dependency,简记为FD)
- 多值依赖(Multivalued Dependency,简记为MVD)
- 其他
四、关系模式的简化表示
关系模式R(U, D, DOM, F)简化为一个三元组:
- R(U, F)
当且仅当U上的一个关系r满足F时,r称为关系模式 R(U, F)的一个关系
五、数据依赖对关系模式的影响
例:建立一个描述学校教务的数据库:学生的学号(Sno)、所在系(Sdept),系主任姓名(Mname)、课程名(Cname),成绩(Grade)
单一的关系模式 :Student <U、F>
U ={ Sno, Sdept, Mname, Cname, Grade }
属性组U上的一组函数依赖F:
F ={ Sno → Sdept, Sdept → Mname, (Sno, Cname) → Grade }
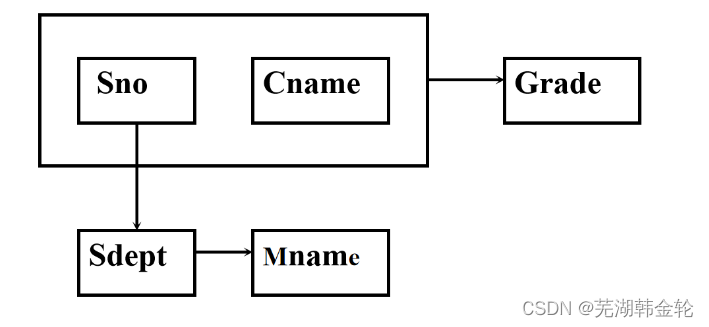
关系模式Student<U, F>中存在的问题
数据冗余太大
- 系主任姓名重复出现,浪费存储空间
更新异常(Update Anomalies)
- 更换系主任?更改系名?
插入异常(Insertion Anomalies)
- 一个系刚成立,尚无学生?
删除异常(Deletion Anomalies)
- 一个系的学生全部毕业了?
结论:
Student关系模式不是一个好的模式。
“好”的模式:不会发生插入异常、删除异常、更新异常,数据冗余应尽可能少
原因:由存在于模式中的某些数据依赖引起的
解决方法:通过分解关系模式来消除其中不合适的数据依赖
6.2 规范化
规范化理论正是用来改造关系模式,通过分解关系模式来消除其中不合适的数据依赖,以解决插入异常、删除异常、更新异常和数据冗余问题。
6.2.1 函数依赖
一、函数依赖
设R(U)是一个属性集U上的关系模式,X和Y是U的子集。
若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等, 而在Y上的属性值不等, 则称 “X函数确定Y” 或 “Y函数依赖于X”,记作X→Y。
说明:
所有关系实例均要满足
语义范畴的概念
数据库设计者可以对现实世界作强制的规定
二、平凡函数依赖与非平凡函数依赖
在关系模式R(U)中,对于U的子集X和Y,
- 如果X→Y,但Y∉X,则称X→Y是非平凡的函数依赖
- 若X→Y,但Y∈X, 则称X→Y是平凡的函数依赖
例:
在关系SC(Sno, Cno, Grade)中,
非平凡函数依赖: (Sno, Cno) → Grade
平凡函数依赖: (Sno, Cno) → Sno ,(Sno, Cno) → Cno
- 若X→Y,则X称为这个函数依赖的决定属性组,也称为决定因素(Determinant)。
- 若X→Y,Y→X,则记作X←→Y。
- 若Y不函数依赖于X,则记作X↛\nrightarrow↛Y。
三、完全函数依赖与部分函数依赖
在R(U)中,如果X→Y,并且对于X的任何一个真子集X’,都有X’$\nrightarrow Y,则称Y对X∗∗完全函数依赖∗∗,记作Y, 则称Y对X**完全函数依赖**,记作Y,则称Y对X∗∗完全函数依赖∗∗,记作X\overset{F}{\rightarrow}Y$
若X→Y,但Y不完全函数依赖于X,则称Y对X部分函数依赖,记作X→PYX\overset{P}{\rightarrow}YX→PY。
(Sno,Cno)→Grade是完全函数依赖,
(Sno,Cno)→Sdept是部分函数依赖,因为Sno →Sdept成立,且Sno是(Sno,Cno)的真子集
四、传递函数依赖
在R(U)中,如果X→Y,(Y∉X) ,Y$\nrightarrow XY→Z,则称Z对X∗∗传递函数依赖∗∗。记为:X Y→Z, 则称Z对X**传递函数依赖**。 记为:XY→Z,则称Z对X∗∗传递函数依赖∗∗。记为:X\overset{传递}{\rightarrow}Z$
注意:如果Y→X, 即X←→Y,则Z直接依赖于X。
在关系Std(Sno, Sdept, Mname)中,有:
Sno → Sdept,Sdept → Mname
则Mname传递函数依赖于Sno
6.2.2 码
候选码:
设K为R<U,F>中的属性或属性组合。若K→FUK\overset{F}{\rightarrow}UK→FU, 则K称为R的侯选码(Candidate Key)。
若候选码多于一个,则选定其中的一个做为主码(Primary Key)。
- 主属性与非主属性
- 包含在任何一个候选码中的属性称为主属性
- 不包含在任何码中的属性称为非主属性或非码属性
整个属性组是码,称为全码(All-key)
外码:
关系模式R中属性或属性组X并非R的码,但X是另一个关系模式的码,则称X是R的外部码(Foreign key)也称外码
- 主码与外部码一起提供了表示关系间联系的手段
6.2.3 范式
-
范式是符合某一种级别的关系模式的集合
-
关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式
范式的种类:
-
第一范式(1NF)
-
第二范式(2NF)
-
第三范式(3NF)
-
BC范式(BCNF)
-
第四范式(4NF)
-
第五范式(5NF)
各种范式之间存在联系:
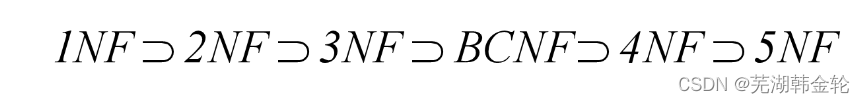
-
某一关系模式R为第n范式,可简记为R∈nNF
规范化:
一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
6.2.4 2NF
1NF:
如果一个关系模式R的所有属性都是不可分的基本数据项,则R∈1NF
- 第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库
- 但是满足第一范式的关系模式并不一定是一个好的关系模式
例:关系模式 S-L-C(Sno, Sdept, Sloc, Cno, Grade)
Sloc为学生住处,假设每个系的学生住在同一个地方
函数依赖包括:
(Sno, Cno) →F\overset{F}{\rightarrow}→F Grade
Sno → Sdept
(Sno, Cno)→P\overset{P}{\rightarrow}→PSdept
Sno → Sloc
(Sno, Cno)→P\overset{P}{\rightarrow}→PSloc
Sdept → Sloc

- S-L-C的码为(Sno, Cno)
- S-L-C满足第一范式
- 非主属性Sdept和Sloc部分函数依赖于码(Sno, Cno)
但S-L-C不是一个好的关系模式
- 插入异常。插入一个学生信息,但学生还没有选课?
- 删除异常。学生取消选课,如果所有选课都取消了?
- 修改复杂。学生转系?住处也要修改
- 数据冗余度大
原因:Sdept、Sloc部分函数依赖于码。
解决方法:S-L-C分解为两个关系模式,以消除这些部分函数依赖
- SC(Sno, Cno, Grade)
- S-L(Sno, Sdept, Sloc)

不存在非主属性对码的部分依赖
2NF:
若R∈1NF,且每一个非主属性完全函数依赖于码,则R∈2NF。
采用投影分解法将一个1NF的关系分解为多个2NF的关系,可以在一定程度上减轻原1NF关系中存在的插入异常、删除异常、数据冗余度大、修改复杂等问题。但并不能完全消除。
判断一个关系是否属于第二范式:
找出数据表中的所有码;
找出所有主属性和非主属性;
判断所有的非主属性对码的部分函数依赖。
6.2.5 3NF
3NF:
关系模式R<U,F> 中若不存在这样的码X、属性组Y及非主属性Z(Y不包含Z), 使得X→Y,Y→Z成立,Y$ \nrightarrow $X,则称R<U,F> ∈ 3NF。
若R∈3NF,则每一个非主属性既不部分依赖于码也不传递依赖于码。
若R∈3NF,当且仅当任何时候,每个元组都含有一个主码来识别实体,同时有一组0个或多个相互独立的属性从不同方面描述这个实体。
6.2.6 BCNF
BCNF:
关系模式R<U,F>∈1NF,若X→Y且X不包含Y时X必含有码,则R<U,F> ∈BCNF。
等价于:每一个决定属性因素都包含码
若R∈BCNF
- 所有非主属性对每一个码都是完全函数依赖
- 所有的主属性对每一个不包含它的码,也是完全函数依赖
- 没有任何属性完全函数依赖于非码的任何一组属性

6.2.7 多值依赖
例:学校中某一门课程由多个教师讲授,他们使用相同的一套参考书。每个教员可以讲授多门课程,每种参考书可以供多门课程使用。
非规范化关系:
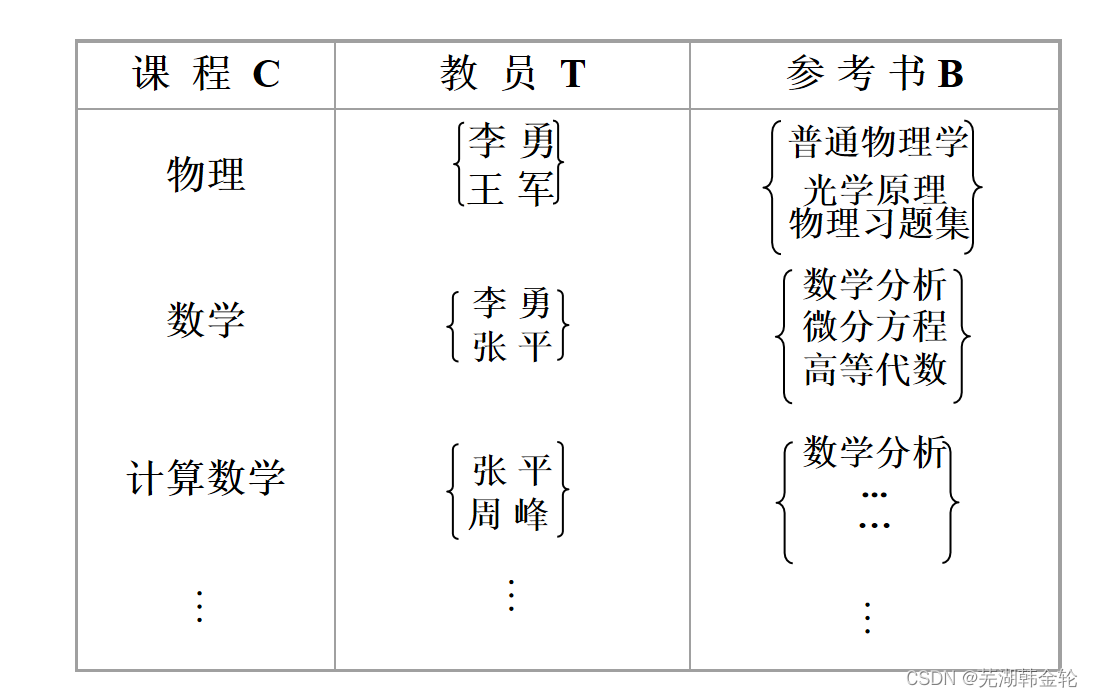
用二维表表示Teaching:

- Teaching∈BCNF
- Teaching具有唯一候选码(C,T,B), 即全码
Teaching模式中存在的问题:
- 数据冗余度大
- 插入操作复杂。某门课程增加一个教员?需要插入多个元组
- 删除操作复杂。某门课程去掉一本参考书?需要删除多个元组
- 修改操作复杂
多值依赖:(真的难记)
设R(U)是一个属性集U上的一个关系模式, X、 Y和Z是U的子集,并且Z=U-X-Y。关系模式R(U)中多值依赖 X→→Y成立,当且仅当对R(U)的任一关系r,给定的一对(x,z)值,有一组Y的值,这组值仅仅决定于x值而与z值无关
多值依赖的另一个等价的形式化的定义:
在R(U)的任一关系r中,如果存在元组t,s 使得t[X]=s[X],那么就必然存在元组 w,v∈ r,(w,v可以与s,t相同),使得w[X]=v[X]=t[X],而w[Y]=t[Y],w[Z]=s[Z],v[Y]=s[Y],v[Z]=t[Z](即交换s,t元组的Y值所得的两个新元组必在r中),则Y多值依赖于X,记为X→→Y。 这里,X,Y是U的子集,Z=U-X-Y。
平凡多值依赖和非平凡的多值依赖
- 若X→→Y,而Z=φ,则称X→→Y为平凡的多值依赖
- 否则称X→→Y为非平凡的多值依赖
多值依赖的性质
(1)多值依赖具有对称性
若X→→Y,则X→→Z,其中Z=U-X-Y
(2)多值依赖具有传递性
若X→→Y,Y→→Z, 则X→→Z –Y
(3)函数依赖是多值依赖的特殊情况。
若X→Y,则X→→Y。
(4)若X→→Y,X→→Z,则X→→Y∪Z。
(5)若X→→Y,X→→Z,则X→→Y∩Z。
(6)若X→→Y,X→→Z,则X→→Y-Z,X→→Z -Y
多值依赖与函数依赖的区别
(1) 多值依赖的有效性与属性集的范围有关
(2)
若函数依赖X→Y在R(U)上成立,则对于任何Y’⊂Y均有X→Y’ 成立
多值依赖X→→Y若在R(U)上成立,不能断言对于任何Y’⊂Y有X→→Y’ 成立
6.2.8 4NF
4NF:
关系模式R<U,F>∈1NF,如果对于R的每个非平凡多值依赖X→→Y(X不包含Y),X都含有码,则R∈4NF。
如果R ∈ 4NF, 则R ∈ BCNF
- 不允许有非平凡且非函数依赖的多值依赖
- 允许的非平凡多值依赖是函数依赖
6.2.9 规范化小结
- 关系数据库的规范化理论是数据库逻辑设计的工具
- 目的:尽量消除插入、删除异常,修改复杂,数据冗余
- 基本思想:逐步消除数据依赖中不合适的部分
- 实质:概念的单一化
关系模式规范化的基本步骤

6.3 数据依赖的公理系统
逻辑蕴含:
对于满足一组函数依赖F的关系模式R <U,F>,其任何一个关系r,若函数依赖X→Y都成立,(即r中任意两元组t,s,若t[X]=s[X],则t[Y]=s[Y]),则称F逻辑蕴含X →Y
Armstrong公理系统
关系模式R <U,F >来说有以下的推理规则:
A1.自反律(Reflexivity):若Y ⊆ X ⊆ U,则X →Y为F所蕴含。
A2.增广律(Augmentation):若X→Y为F所蕴含,且Z ⊆ U,则XZ→YZ为F所蕴含。
A3.传递律(Transitivity):若X→Y及Y→Z为F所蕴含,则X→Z为F所蕴含。
导出规则:
根据A1,A2,A3这三条推理规则可以得到下面三条推理规则:
合并规则:由X→Y,X→Z,有X→YZ。(A2, A3)
伪传递规则:由X→Y,WY→Z,有XW→Z。(A2, A3)
分解规则:由X→Y及 Z⊆Y,有X→Z。(A1, A3)
引理1:
X→A1 A2…Ak成立的充分必要条件是X→Ai成立(i=l,2,…,k)
函数依赖闭包
在关系模式R<U,F>中为F所逻辑蕴含的函数依赖的全体叫作F的闭包,记为F+。
例:

Armstrong公理系统是有效的、完备的
- 有效性:由F出发根据Armstrong公理推导出来的每一个函数依赖一定在F+中;
- 完备性:F+中的每一个函数依赖,必定可以由F出发根据Armstrong公理推导出来
设F为属性集U上的一组函数依赖,X⊆U, XF+ ={A|X→A能由F 根据Armstrong公理导出},XF+称为属性集X关于函数依赖集F的闭包
求闭包的算法:

例:背下这些详细步骤

候选码求解方法
对关系模式R<U,F>,选取可能是候选码的属性集,求其函数依赖闭包,如果属性集的函数依赖闭包=U,则该属性集为候选码
三类属性
L类:仅出现在F的函数依赖左边
R类:仅出现在F的函数依赖右边
N类:没有出现在F的函数依赖中定理1:L类属性必为任一候选码的成员
定理2:R类属性不在任何候选码中
定理3:N类属性必包含在任何候选码中


最小函数依赖集
定义:如果函数依赖集F满足以下条件,则称F为一个极小函数依赖集。也称为最小依赖集或最小覆盖。
(1)F中任一函数依赖的右部仅含有一个属性。
(2)F中不存在这样的函数依赖X→A,使得F与F-{X→A}等价。
(3)F中不存在这样的函数依赖X→A,X有真子集Z使得F-{X→A}U{Z→A}与F等价。
最小依赖集通用算法:
① 用分解的法则,使F中的任何一个函数依赖的右部仅含有一个属性;
② 去掉多余的函数依赖:从第一个函数依赖X→Y开始将其从F中去掉,然后在剩下的函数依赖中求X的闭包X+,看X+是否包含Y,若是,则去掉X→Y;否则不能去掉,依次做下去。直到找不到冗余的函数依赖;
③ 去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖。例如XY→A,若要判Y为多余的,则以X→A代替XY→A是否等价?若A属于(X)+,则Y是多余属性,可以去掉。(以上步骤中,求出关系依赖集F,此时,在F的基础上,求出X或者Y的闭包,是否包含A)注意:第三步求闭包使用的依赖集是第二步求出时的。
例:关系模式R(U,F)中,U=ABCDEG,F={B->D,DG->C,BD->E,AG->B,ADG->BC};求F的最小函数依赖集



最后建议这章还是找点题目来做,也是有一定占比的
随便找的几篇:
http://t.csdn.cn/aFuG9
http://t.csdn.cn/cUnNC考试更会考这种贴近生活的例子
相关文章:

《数据库系统概论》学习笔记——第六章 关系数据理论
教材为数据库系统概论第五版(王珊) 这一章重点在于各种范式的概念和将低级范式转为高级范式。一定要看多值依赖和4NF(因为这个概念很绕又烦,但是期中期末都考了)。最后计算题就是一定要会:算闭包࿰…...
Odoo | Webserivce | 5分钟学会【JSONRPC】接口开发
文章目录Odoo - JsonRPC1. Odoo内方法结构(接收端)2. POST接口请求结构(发送端)3. 实例测试Odoo - JsonRPC 1. Odoo内方法结构(接收端) # -*- coding: utf-8 -*- import odoo import logging import trac…...
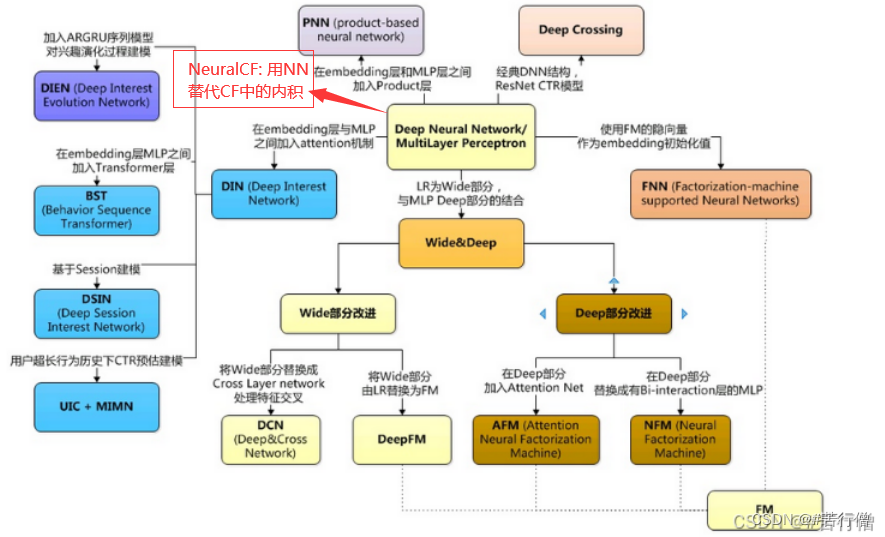
搜广推 NeuralCF - 改进协同过滤+矩阵分解的思想
😄 NeuralCF:2017新加坡国立大学提出。【后文简称NCF】 😄 PNN:2016年上海交通大学提出。 文章目录 NeuralCF动机原理general NCFNCF终极版(GMF+MLP的结合)缺点优点ReferenceNeuralCF 动机 前面学了MF,可知MF在用户-物品评分矩阵的基础上做矩阵分解(用户矩阵Q和物品…...
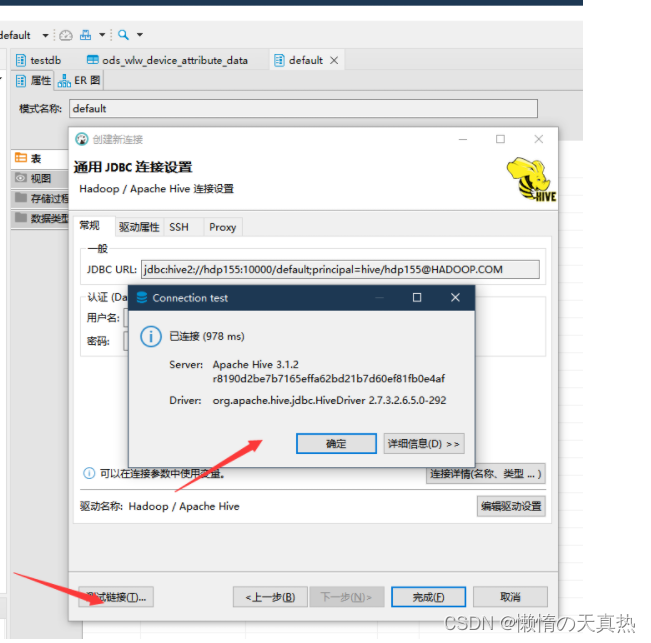
dbever连接kerberos认证的hive
文章目录一、本地安装kerberos客户端二、本地kerberos客户端登录三、dbever连接hive一、本地安装kerberos客户端 下载地址:https://web.mit.edu/kerberos/dist/index.html 安装:下一步或者自定义安装即可 安装后会自动生成配置文件:C:\Pro…...
pom依赖产生的各种问题
文章目录问题一(org.apache.ibatis.session.Configuration)解决方法问题二(ERROR StatusLogger No log4j2)解决方法问题三(com.google.common.util.concurrent)解决方法问题四(start bean documentationPluginsBootstrapper)解决方法问题五(Unable to infer base url. )解决办法…...
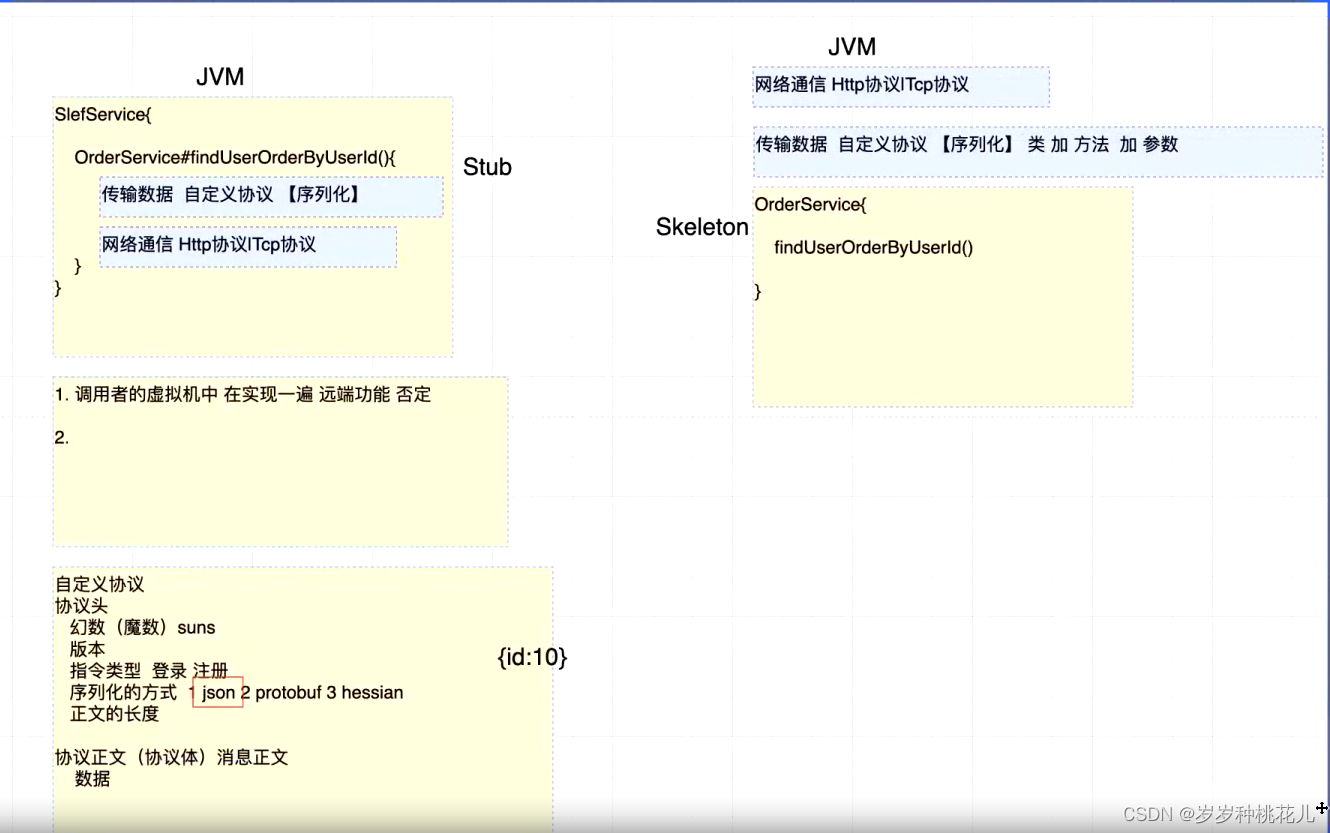
RPC编程:RPC框架设计目标
一:前导知识 Http是超文本传输协议,跨平台性非常好。Http可以传输文本,更多的时候传输的是文本,我们也是可以传输二进制的,我们基于Http进行下载的时候,就是走的Http协议。 Tcp协议,处理的时候…...

RBAC 权限模型介绍
RBAC 权限: 一、关系: 这基于角色的访问控制的结构就叫RBAC结构。 二、RBAC 重要对象: 用户(Employee):角色施加的主体;用户通过拥有某个或多个角色以得到对应的权限。角色(Role&…...
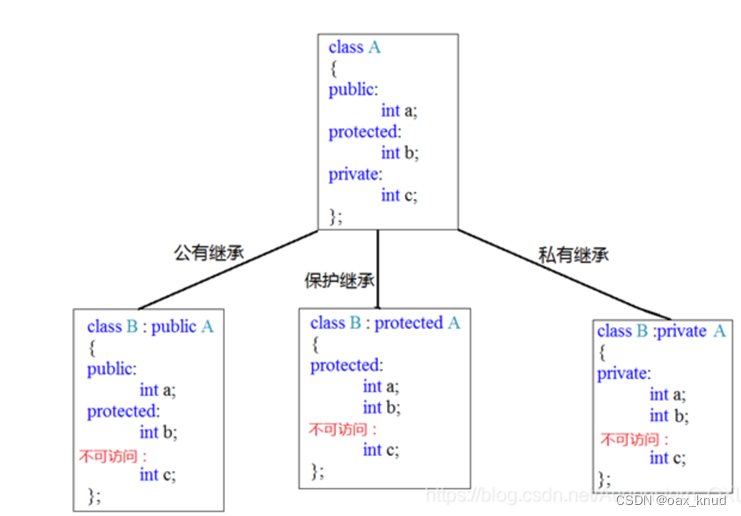
西电面向对象程序设计核心考点汇总(期末真题)
文章目录前言一、往年真题与答案1.1 改错题1.2 读程题1.3 面向对象程序设计二、易错知识点2.1 构造函数2.2 静态成员变量和静态成员函数2.3 权限2.4 继承2.5 多态总结前言 主要针对西安电子科技大学《面向对象程序设计》的核心考点进行汇总,包含总共8章的核心简答。…...

判断一个用字符串表达的数字是否可以被整除
一.问题引出 当一个数字很大的时候,我们常用字符串进行表达,(超过了int和long等数据类型可以存储的最大范围),但是这个时候我们该如何判断他是否可以被另一个数整除呢? 这个时候我们不妨这样来考虑问题,每次将前边求模之后的数保存下来,然后乘以10和这一位的数字进行相加的操…...
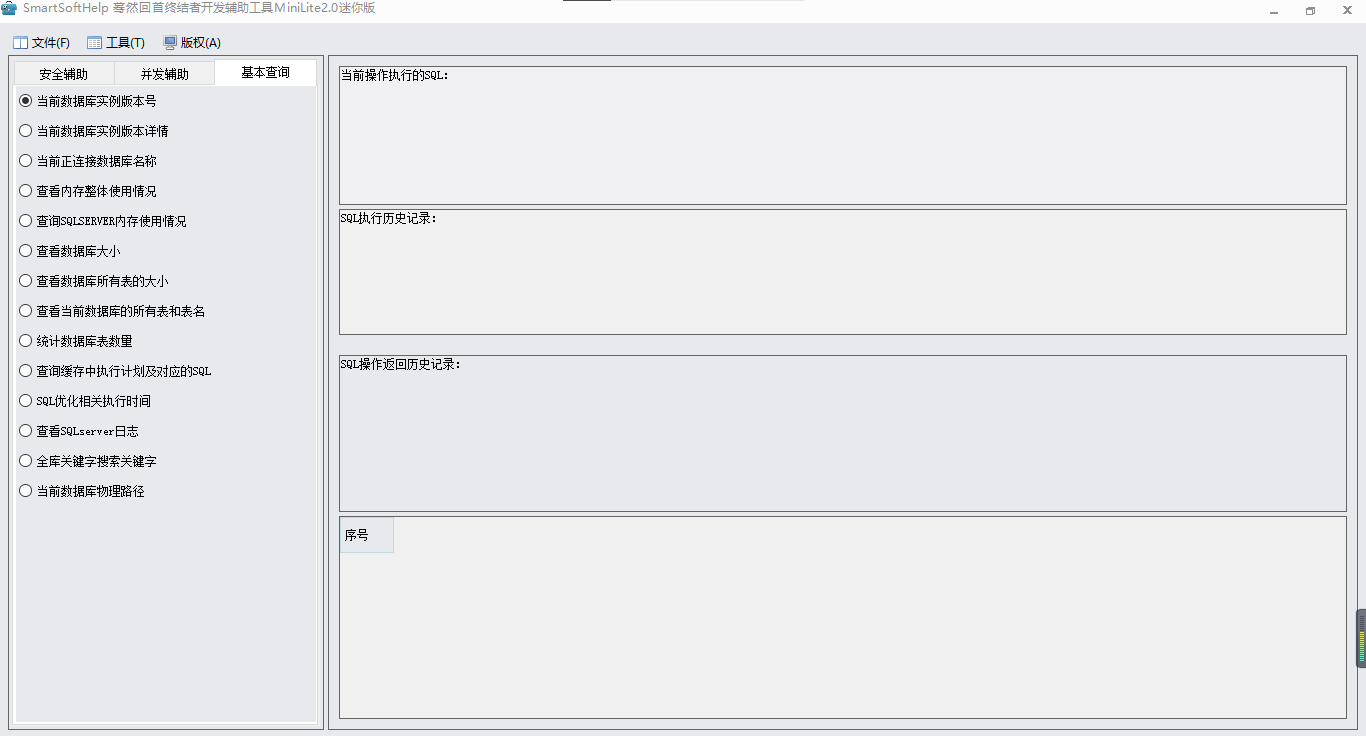
这是一款值得开发人员认真研究的软件,数据库优化,应用服务器安全优化...
1.查询数据库死锁相关信息2.查看数据库的链接情况3.当前实例上的所有用户4.创建数据库独立密码5.查看数据库使用的端口号6.当前数据库设置的最大连接数7.当前数据库最大的理论可连接数8.当前数据库实例的连接数9.当前数据库连接数10.当前数据库连接超时设置11.当前sqlserver 超…...
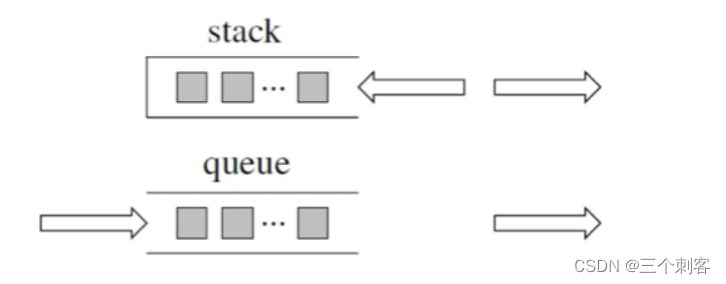
栈与队列小结
一、理论基础1.队列是先进先出,栈是先进后出2.栈和队列是STL(C标准库)里面的两个数据结构。栈提供push和pop等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器。3.栈是以底层容器…...

SpringBoot整合(五)HikariCP、Druid数据库连接池—多数据源配置
在项目中,数据库连接池基本是必不可少的组件。在目前数据库连接池的选型中,主要是 Druid ,为监控而生的数据库连接池。HikariCP ,号称性能最好的数据库连接池。 在Spring Boot 2.X 版本,默认采用 HikariCP 连接池。而…...
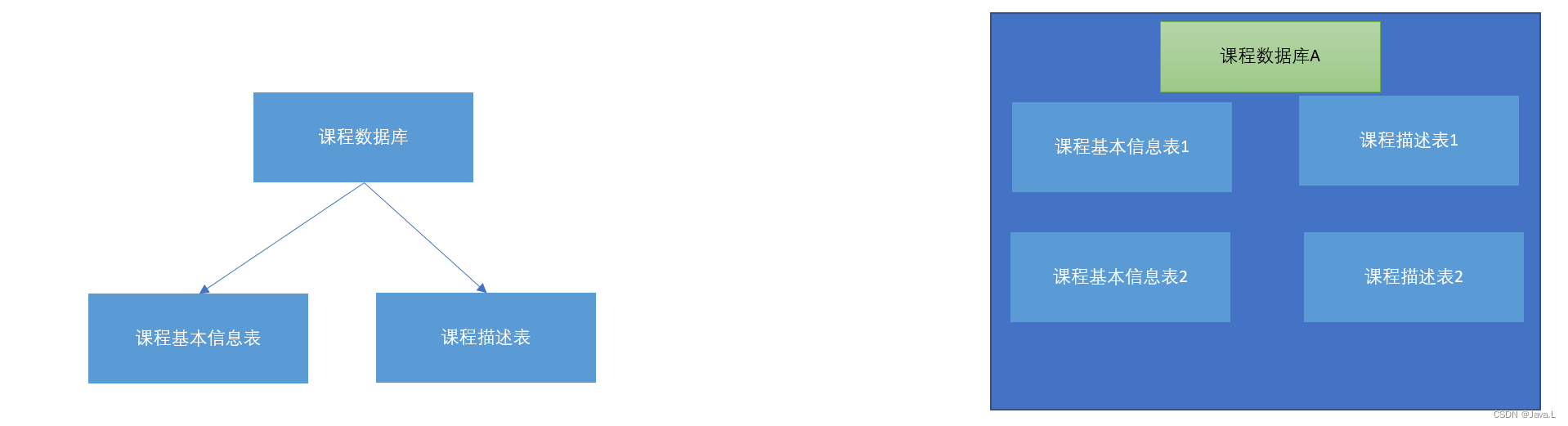
ShardingSphere水平、垂直分库、分表和公共表
目录一、ShardingSphere简介二、ShardingSphere-分库分表1、垂直拆分(1)垂直分库(2)垂直分表2、水平拆分(1)水平分库(2)水平分表三、水平分库操作1、创建数据库和表2、配置分片的规则…...

《分布式技术原理与算法解析》学习笔记Day24
分布式缓存 在计算机领域,缓存是一个非常重要的、用来提升性能的技术。 什么是分布式缓存? 缓存技术是指用一个更快的存储设备存储一些经常用到的数据,供用户快速访问。 分布式缓存是指在分布式环境或者系统下,把一些热门数据…...

强化学习RL 02: Value-based Reinforcement Learning
DQN和TD更新算法。 目录 Review 1. Deep Q-Network(DQN) 1.1 Approximate the Q*(s,a) Function 1.2 Apply DQN to Play Game 1.3 Temporal Difference(TD) Learning 1.4 TD Learning for DQN 1.4.1 TD使用条件 condition 1.4.2 Train DQN using TD learning 1.5 summ…...
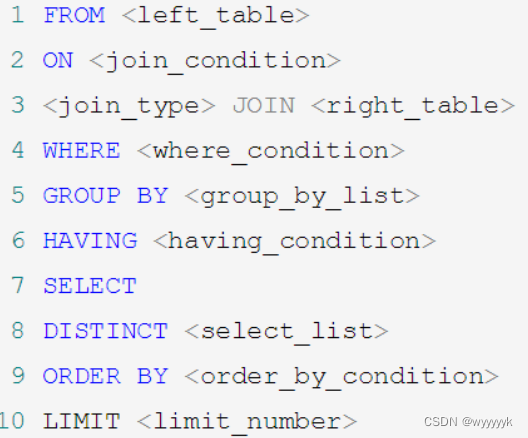
08_MySQL聚合函数
1. 聚合函数介绍什么是聚合函数聚合函数作用于一组数据,并对一组数据返回一个值。聚合函数类型AVG()SUM()MAX()MIN()COUNT()注意:聚合函数不能嵌套调用。比如不能出现类似“AVG(SUM(字段名称))”形式的调用。1.1 AVG和SUM函数可以对数值型数据使用AVG 和…...

「TCG 规范解读」词汇表
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
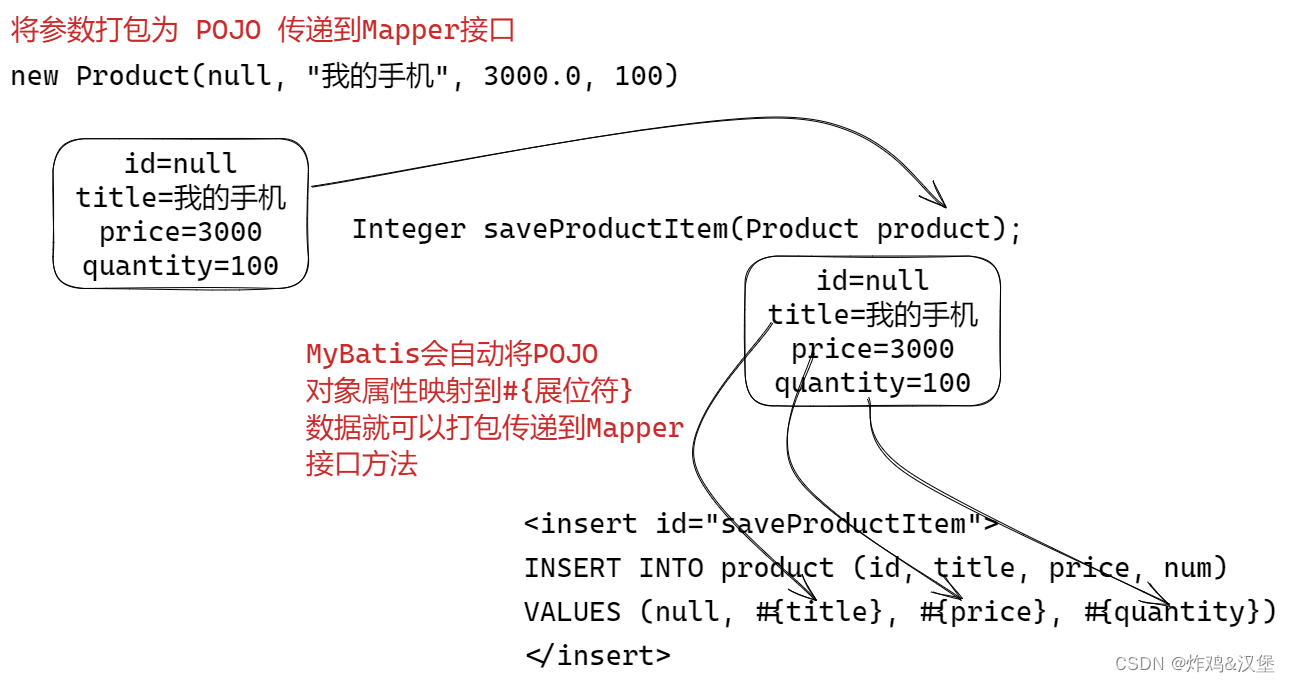
第三阶段-03MyBatis 中使用XML映射文件详解
MyBatis 中使用XML映射文件 什么是XML映射 使用注解的映射SQL的问题: 长SQL需要折行,不方便维护动态SQL查询拼接复杂源代码中的SQL,不方便与DBA协作 MyBatis建议使用XML文件映射SQL才能最大化发挥MySQL的功能 统一管理SQL, 方…...

从0开始学python -41
Python3 命名空间和作用域 命名空间 先看看官方文档的一段话: A namespace is a mapping from names to objects.Most namespaces are currently implemented as Python dictionaries。 命名空间(Namespace)是从名称到对象的映射,大部分的命名空间都是…...
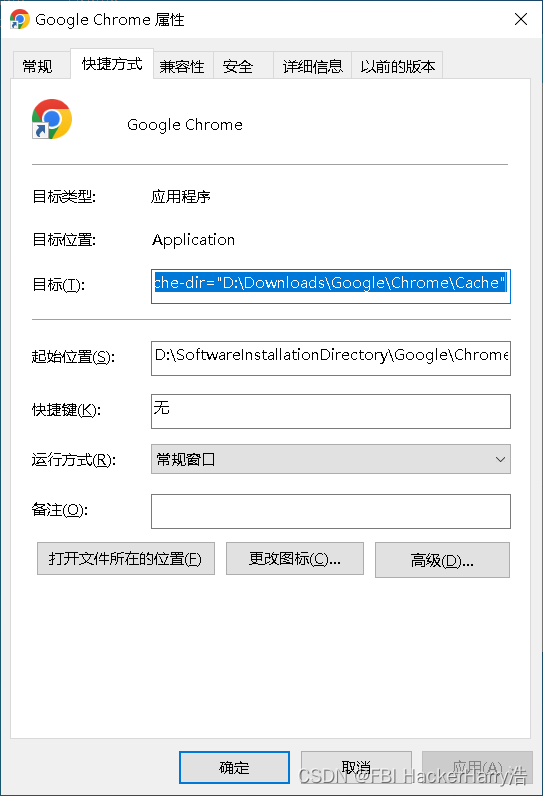
如何将Google浏览器安装到D盘(内含教学视频)
如何将Google浏览器安装到D盘(内含教学视频) 教学视频下载链接地址:https://download.csdn.net/download/weixin_46411355/87503968 目录如何将Google浏览器安装到D盘(内含教学视频)教学视频下载链接地址:…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
