【数据结构与算法】前缀树的实现
🌠作者:@阿亮joy.
🎆专栏:《数据结构与算法要啸着学》
🎇座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根
目录
- 👉前缀树的实现👈
- 什么是前缀树
- 节点的定义
- 构造函数
- 插入字符串
- 查找字符串和前缀
- 析构函数
- 删除字符串
- 打印前缀树
- 完整代码
- OJ题:实现前缀树
- 👉总结👈
👉前缀树的实现👈
什么是前缀树
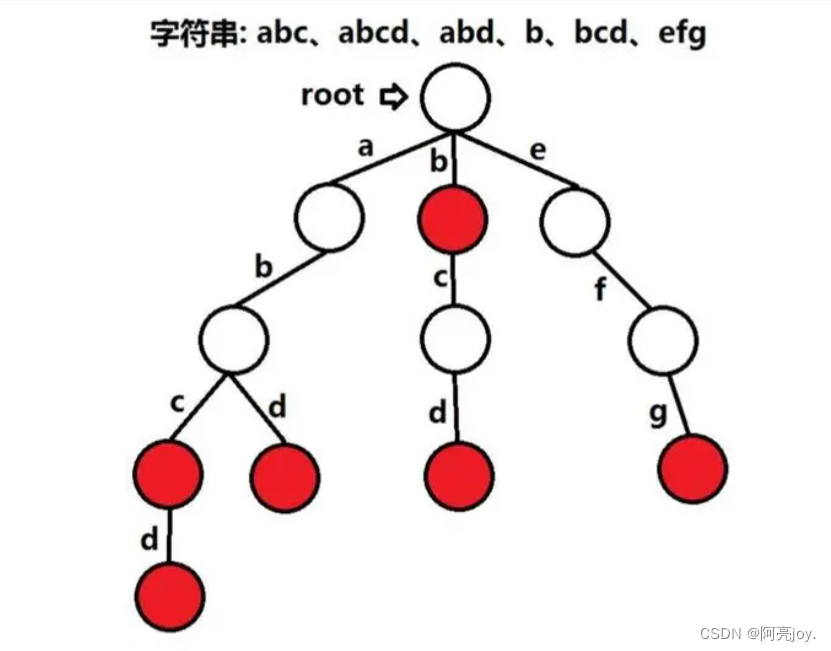
Trie(发音类似 “try”),被称为前缀树或字典树,是一种树形的数据结构,可用于高效地存储和检索字符串数据集中的键。这个数据结构有相当多的应用情景,例如自动补完和拼写检查。下图就是经典的前缀树,我们接下来要实现的前缀树的节点存储的数据比较丰富,以达到特定字符串在树中出现几次等类似的功能。
节点的定义
// 前缀树节点的定义
// 假设字符都是小写字母
struct TrieNode
{int pass = 0; // 有几个字符串经过该节点(前缀包含这个字符的字符串数量)int end = 0; // 以该节点为结尾的字符串的数量,如果不允许字符串重复插入,可以改成bool// next[0] == nullptr 表示没有走向'a'的路// next[0] != nullptr 表示有走向'a'的路// ...// next[25] != nullptr 表示有走向'z'的路TrieNode* next[26] = { nullptr }; // 26个空位,准备挂下一个节点'a'-'z',没有挂节点时为nullptr// 如果字符种类个数比较多,可以将数组换成哈希表或者set
};
构造函数
前缀树是用哨兵位头节点来管理整棵前缀树的,所以其构造函数需要 new 上一个哨兵位头节点。
class Trie
{typedef TrieNode Node;
public:Trie(){_root = new Node();}
private:Node* _root = nullptr; // 哨兵位头节点,可以用来求前缀树中字符串的数量,也可以求空串的数量
};
注:哨兵位头节点的 pass 值可以表示前缀树含有的字符串数量,end 值可以表示前缀树含有空串的数量。因为任何字符串都会以空串作为前缀,都会经过哨兵位头节点。
插入字符串
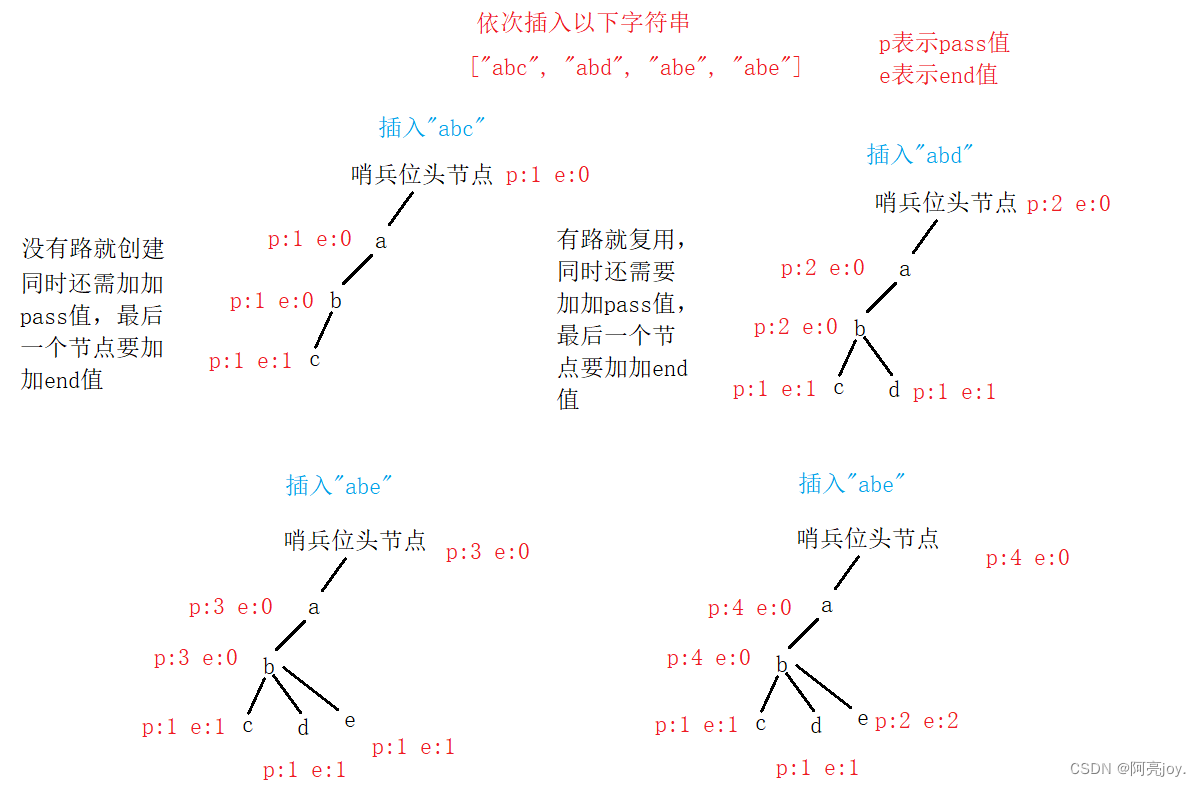
我们从哨兵位头节点开始,插入字符串。对于当前字符对应的子节点,有以下两种情况:
- 子节点存在:沿着指针移动到子节点,继续处理下一个字符。
- 子节点不存在:创建一个新的子节点,记录在 next 指针数组的对应的位置上,然后沿着指针移动到子节点,继续处理下一个字符。
- 插入字符串的同时,还需要更新沿途节点的 pass 值。
插入字符串图解:
class Trie
{
public:void Insert(const string& str){Node* cur = _root;++cur->pass; // 任何一个字符串都需要经过哨兵位头节点for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果之前没有字符串经过该节点,则需要建出新节点if (cur->next[index] == nullptr){cur->next[index] = new Node();}cur = cur->next[index];++cur->pass;}// cur指向字符串的最后一个节点,++cur->end表示多了一个字符串以该节点结尾++cur->end;}
}
如果不需要插入重复字符串,可以将函数的返回值改成 bool 类型。
查找字符串和前缀
class Trie
{
public:// 查找前缀树中有多少个要查找的字符串size_t Search(const string& str) const{Node* cur = _root;for (auto ch : str){// 找的过程发现没路了,说明树中不存在要查找的字符串if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur是str最后一个字符,cur->end表示树中有多少个strreturn cur->end;}// 查找树中有多少个字符串以前缀prefix为前缀size_t StartsWith(const std::string& prefix) const{Node* cur = _root;for (auto ch : prefix){// 找的过程中发现没有路,则说明没有字符串以prefix为前缀if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur->pass表示有多少个字符串以prefix为前缀return cur->pass;}
}
注:查找的过程和插入的过程非常的相似,只是查找时发现没有路,就直接返回 0,表示树中没有该字符串或者树中的字符串不以 prefix 为前缀。注:如果树中有要查找的字符串 str,则 cur->end 表示树中有多少个 str;如果树有字符串以 prefix 为前缀,则 cur->pass 表示多少个字符串以 prefix 为前缀。
析构函数
class Trie
{typedef TrieNode Node;
public:~Trie(){Destroy(_root);}
private:void Destroy(Node* root){// 先销毁孩子节点,才能够销毁自己for (int i = 0; i < 26; ++i){// root->next[i]不为空,则说明有节点,需要递归释放节点if (root->next[i] != nullptr){Destroy(root->next[i]);}}delete root;}
}
前缀树析构时,需要先释放孩子节点,才能够释放哨兵位头节点。而孩子节点有可能会有孩子节点,所以我们可以采用递归去释放节点。
删除字符串
class Trie
{typedef TrieNode Node;
public:// 从树中删除字符串str,注:如果有多个str,只会删除一次void Erase(const string& str){// 树中没有str,无法删除if (Search(str) == 0)return;Node* cur = _root;--cur->pass;for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果发现str是唯一经过该节点的字符串// 那么就需要递归去释放当前节点及后续路径的节点if (--cur->next[index]->pass == 0){Destroy(cur->next[index]); // 递归释放节点cur->next[index] = nullptr; // next需要置为nullptrreturn;}cur = cur->next[index];}// 如果字符串的所有字符都删除了一遍,还有该路径,那么最后要// --cur->end,表明树中str的个数减少了一个--cur->end;}
}
删除字符串时,需要看树中是否有需要删除的字符串。如果没有,直接 return 即可。如果有,才进行删除。进行删除时,如果发现 str 是唯一经过该节点的字符串,那么就需要递归去释放当前节点及后续路径的节点。
打印前缀树
class Trie
{typedef TrieNode Node;
public:void Print() const{cout << "根节点:[" << "pass: " << _root->pass << " end: " << _root->end << "]" << endl;_Print(_root);}
private:void _Print(Node* root) const{if (root == nullptr)return;for (int i = 0; i < 26; ++i){if (root->next[i] == nullptr)continue;else{cout << "节点" << (char)('a' + i) << ":[pass: " << root->next[i]->pass << " end: " << root->next[i]->end << "]" << endl;_Print(root->next[i]);}}}
}
完整代码
#pragma once#include <vector>
#include <string>
#include <iostream>
using namespace std;// 前缀树节点的定义
// 假设字符都是小写字母
struct TrieNode
{int pass = 0; // 有几个字符串经过该节点(前缀包含这个字符的字符串数量)int end = 0; // 以该节点为结尾的字符串的数量,如果不允许重复插入,可以改成bool// next[0] == nullptr 表示没有走向'a'的路// next[0] != nullptr 表示有走向'a'的路// ...// next[25] != nullptr 表示有走向'z'的路TrieNode* next[26] = { nullptr }; // 26个空位,准备挂下一个节点'a'-'z',没有挂节点时为nullptr// 如果字符种类个数比较多,可以将数组换成哈希表或者set
};class Trie
{typedef TrieNode Node;
public:Trie(){_root = new Node();}~Trie(){Destroy(_root);}// 查找前缀树中有多少个要查找的字符串size_t Search(const string& str) const{Node* cur = _root;for (auto ch : str){// 找的过程发现没路了,说明树中不存在要查找的字符串if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur是str最后一个字符,cur->end表示树中有多少个strreturn cur->end;}// 查找树中有多少个字符串以前缀prefix为前缀size_t StartsWith(const std::string& prefix) const{Node* cur = _root;for (auto ch : prefix){// 找的过程中发现没有路,则说明没有字符串以prefix为前缀if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur->pass表示有多少个字符串以prefix为前缀return cur->pass;}// 插入字符串void Insert(const string& str){Node* cur = _root;++cur->pass; // 任何一个字符串都需要经过哨兵位头节点for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果之前没有字符串经过该节点,则需要建出新节点if (cur->next[index] == nullptr){cur->next[index] = new Node();}cur = cur->next[index];++cur->pass;}// cur指向字符串的最后一个节点,++cur->end表示多了一个字符串以该节点结尾++cur->end;}// 从树中删除字符串str,注:如果有多个str,只会删除一次void Erase(const string& str){// 树中没有str,无法删除if (Search(str) == 0)return;Node* cur = _root;--cur->pass;for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果发现str是唯一经过该节点的字符串// 那么就需要递归去释放当前节点及后续路径的节点if (--cur->next[index]->pass == 0){Destroy(cur->next[index]); // 递归释放节点cur->next[index] = nullptr; // next需要置为nullptrreturn;}cur = cur->next[index];}// 如果字符串的所有字符都删除了一遍,还有该路径,那么最后要// --cur->end,表明树中str的个数减少了一个--cur->end;}void Print() const{cout << "根节点:[" << "pass: " << _root->pass << " end: " << _root->end << "]" << endl;_Print(_root);}private:void Destroy(Node* root){// 先销毁孩子节点,才能够销毁自己for (int i = 0; i < 26; ++i){if (root->next[i] != nullptr){Destroy(root->next[i]);}}delete root;}void _Print(Node* root) const{if (root == nullptr)return;for (int i = 0; i < 26; ++i){if (root->next[i] == nullptr)continue;else{cout << "节点" << (char)('a' + i) << ":[pass: " << root->next[i]->pass << " end: " << root->next[i]->end << "]" << endl;_Print(root->next[i]);}}}private:Node* _root = nullptr; // 哨兵位头节点,可以用来求前缀树中字符串的数量,也可以求空串的数量
};
前缀树的测试
void TrieTest()
{Trie t;vector<string> v = { "abc","abd", "abe", "abe", "" ,"a" , "bc", "bd", "be" };for (string& str : v){t.Insert(str);}// 前缀树的打印t.Print();cout << "----------------------" << endl;// 输出空串的数量cout << "空串的数量: " << t.Search("") << endl;// 任意字符串均以空串为前缀/树中字符串的数量cout << "树中字符串的数量: " << t.StartsWith("") << endl;// 以"ab"为前缀的字符串个数cout << "以ab为前缀的字符串个数: " << t.StartsWith("ab") << endl;cout << "----------------------" << endl;// 测试删除for (string& str : v){t.Erase(str);}t.Print();
}

OJ题:实现前缀树
LeetCode 上的实现前缀树是比我们实现的前缀树是要难度低的,所以只需要将上面的代码拷贝过去,再将函数名和函数的返回值修改成题目要求的样子就可以通过了。
👉总结👈
本篇博客主要讲解了什么是前缀树以及前缀树的实现等。那么以上就是本篇博客的全部内容了,如果大家觉得有收获的话,可以点个三连支持一下!谢谢大家!💖💝❣️
相关文章:

【数据结构与算法】前缀树的实现
🌠作者:阿亮joy. 🎆专栏:《数据结构与算法要啸着学》 🎇座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉…...
canvas 制作2048
效果展示 对UI不满意可以自行调整,这里只是说一下游戏的逻辑,具体的API调用不做过多展示。 玩法分析 2048 的玩法非常简单,通过键盘的按下,所有的数字都向着同一个方向移动,如果出现两个相同的数字,就将…...

playwright: 全局修改页面等待超时时间
等待超时时间默认是30s, 可以通过以下几个方法设置: browser_context.set_default_navigation_timeout()browser_context.set_default_timeout()page.set_default_navigation_timeout()page.set_default_timeout() set_default_navigation_timeout set_default_n…...

C++类和对象(中)
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 I do not believe in taking the right decision. I take a decision and make it right. 我不相信什么正确的决定。我都是先做决定,然后把…...

Docker安装EalasticSearch、Kibana,安装Elasticvue插件
使用Docker快速安装部署ES和Kibana的前提:首先需要确保已经安装了Docker环境。 如果没有安装Docker的话,先在Linux上安装Docker。 有了Docker环境后,就可以使用Docker安装部署ES和Kibana了 一、安装ES 1、拉取EalasticSearch镜像 docker p…...

算法训练营 day39 贪心算法 无重叠区间 划分字母区间 合并区间
算法训练营 day39 贪心算法 无重叠区间 划分字母区间 合并区间 无重叠区间 435. 无重叠区间 - 力扣(LeetCode) 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互…...
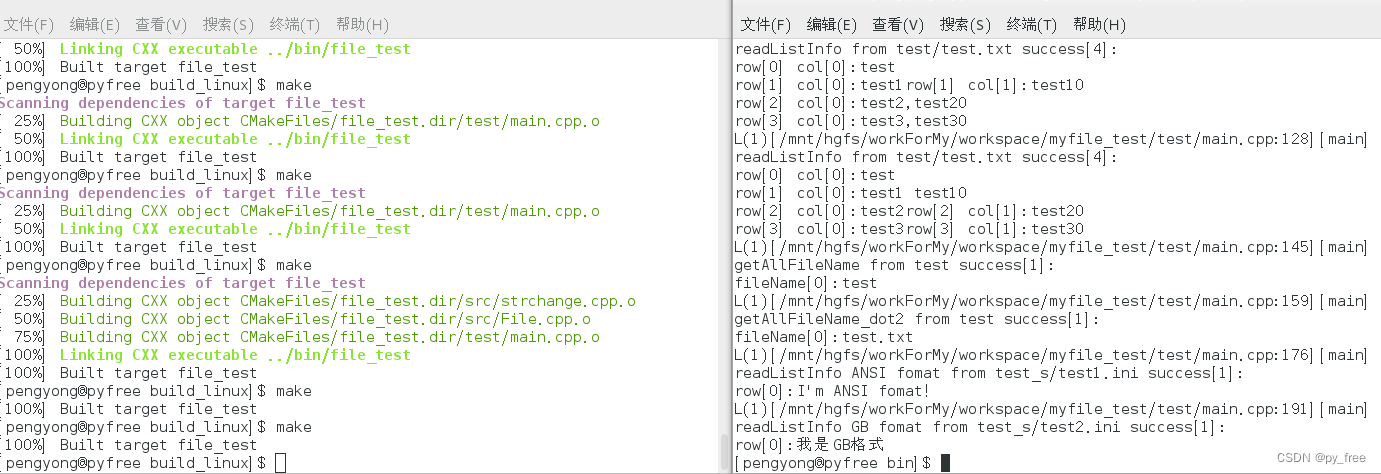
c/c++开发,无可避免的文件访问开发案例
一、缓存文件系统 ANSI C标准中的C语言库提供了fopen, fclose, fread, fwrite, fgetc, fgets, fputc, fputs, freopen, fseek, ftell, rewind等标准函数,这些函数在不同的操作系统中应该调用不同的内核API,从而支持开发者跨平台实现对文件的访问。 在Lin…...

MySQL学习笔记
MySQL学习笔记一、基础配置二、数据库操作三、表的操作1.创建表2.表选项3.查看表4.修改表5.删除表6.复制表7.检查优化修复表四、数据操作基础增删改查五、字符集编码六、数据类型(列类型)1.数值类型2.字符串类型3.日期时间类型4.枚举和集合七、列属性&am…...
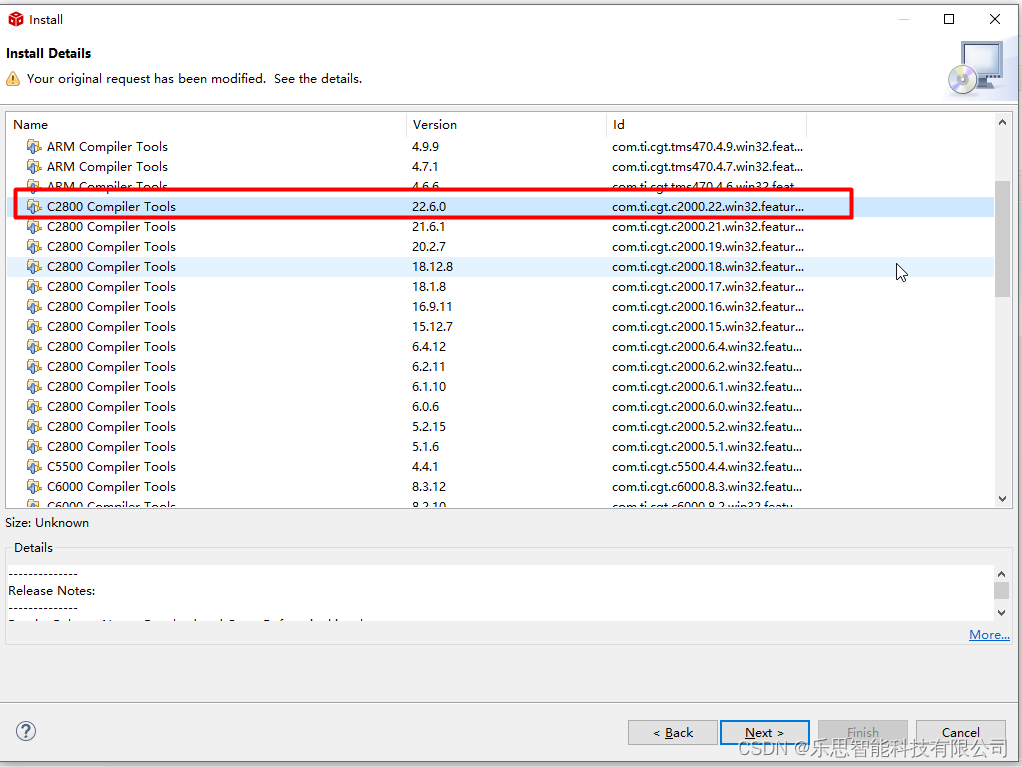
ccs导入工程失败的处理方法
文章目录当导入CCS新工程时出现下述错误怎么办?方法一 从TI官网下载安装包进行安装,下载链接:软件下载完成 安装路径为上面的文件夹点击安装完成后,导入安装路径,并点击Refresh按钮,依据路径进行更新&#…...

探针台常见的故障及解决方法
症状、 可能原因、 解决方法 移动样品后画面变模糊 —显微镜不垂直,调垂直显微镜 样品台不水平 —调水平样品台 显微镜视场亮度不足,边缘切割或看不到像—转换器不在定位位置上 把转换器转到定位位置上 管镜转盘不在定位位置上 —把管镜转盘转到定…...

域内资源探测
✅作者简介:CSDN内容合伙人、信息安全专业在校大学生🏆 🔥系列专栏 :内网安全 📃新人博主 :欢迎点赞收藏关注,会回访! 💬舞台再大,你不上台,永远是…...
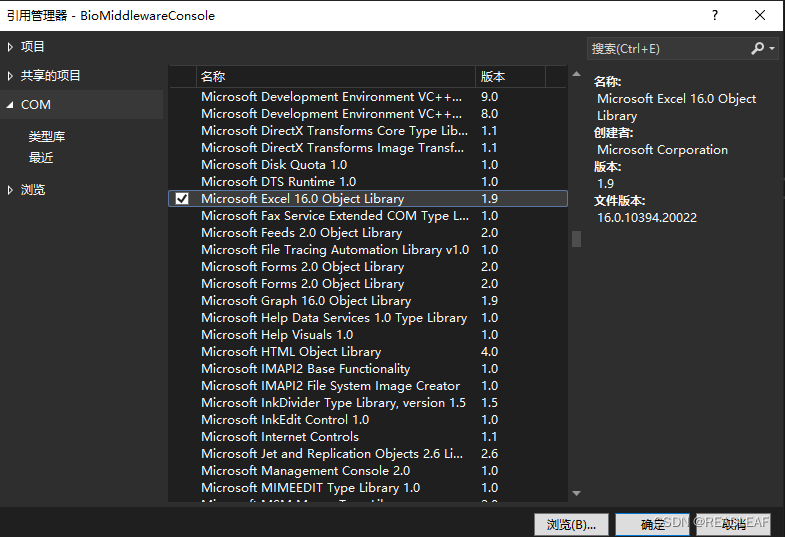
c# 将数据导出到EXCEL文件
第一步:项目中加入引用。 在鼠标右击项目,点击【添加】弹出菜单列表,选择【项目引用】弹出【引用管理器】对话框,选择【COM】-【Microsoft Excel 16.0 Object Library】,如图所示: 第二步,编辑…...
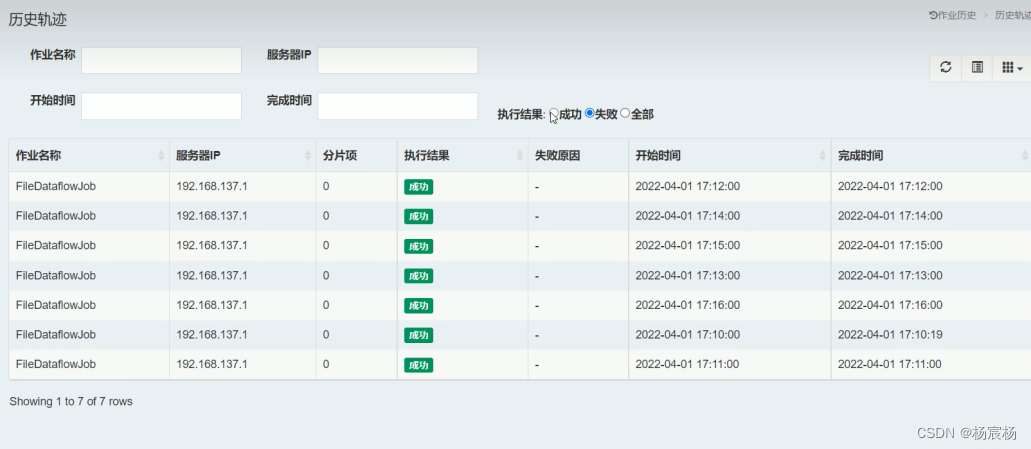
微服务 分片 运维管理
微服务 分片 运维管理分片分片的概念分片案例环境搭建案例改造成任务分片Dataflow类型调度代码示例运维管理事件追踪运维平台搭建步骤使用步骤分片 分片的概念 当只有一台机器的情况下,给定时任务分片四个,在机器A启动四个线程,分别处理四个…...

批量占满TEMP表空间问题处理与排查
批量占满TEMP表空间问题处理与排查应急处置问题排查查看占用TEMP表空间高的SQL获取目标SQL执行计划方法一:EXPLAIN PLAN FOR方法二:DBMS_XPLAN.DISPLAY_CURSOR方法三:DBMS_XPLAN.DISPLAY_AWR方法四:AUTOTRACE数据库跑批任务占满TE…...

Pytorch中的tensor和variable
Tensor与Variable pytorch两个基本对象:Tensor(张量)和Variable(变量) 其中,tensor不能反向传播,variable可以反向传播(forword)。 反向传播是为了让神经网络更新前面…...
暗月内网渗透实战——项目七
首先环境配置 VMware的网络配置图 环境拓扑图 开始渗透 信息收集 使用kali扫描一下靶机的IP地址 靶机IP:192.168.0.114 攻击机IP:192.168.0.109 获取到了ip地址之后,我们扫描一下靶机开放的端口 靶机开放了21,80,999,3389,5985,6588端口…...

【Java 面试合集】描述下Objec类中常用的方法(未完待续中...)
描述下Objec类中常用的方法 1. 概述 首先我们要知道Object 类是所有的对象的基类,也就是所有的方法都是可以被重写的。 那么到底哪些方法是我们常用的方法呢??? cloneequalsfinalizegetClasshashCodenotifynotifyAlltoStringw…...

SQLSERVER 的 truncate 和 delete 有区别吗?
一:背景 1. 讲故事 在面试中我相信有很多朋友会被问到 truncate 和 delete 有什么区别 ,这是一个很有意思的话题,本篇我就试着来回答一下,如果下次大家遇到这类问题,我的答案应该可以帮你成功度过吧。 二࿱…...

【C++】CC++内存管理
就是你被爱情困住了?Wake up bro! 文章目录一、C/C内存分布二、C语言中动态内存管理方式三、C中内存管理方式1.new和delete操作内置类型2.new和delete操作自定义类型(仅限vs的底层实现机制,new和delete一定要匹配使用,…...

数据预处理之图像去空白
数据预处理之图像去空白图像去空白介绍方法边缘检测阈值处理形态学图像剪切图像去空白 介绍 图像去空白是指在图像处理中去除图像中的空白区域的过程。空白区域通常是指图像中的白色或其他颜色,其不包含有用的信息。去空白的目的是为了节省存储空间、提高图像处理…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...