数组中只出现一次的两个数字(异或法思路)
题目简介
一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b
用HashMap记录就不说了。
这里记录一下用异或的方式解决。
- 由于异或特性为自己异或自己为0。a^a = 0;
- 所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉了。
- 又a != b 因此,a^b 的结果在二进制中,肯定有一位是1。这个也好理解。
下面就是我半天不能理解的点了。这里记录一下。
上面说a^b 肯定有一位是1。然后通过遍历数组的所有项,以这一位是不是为1分成两组。
我就很纳闷,理解了很久,为什么以这个条件分成两组。
后来终于想到
因为a^b至少有一位是1的话,那么在a 和b的二进制当中,这一位一定是1个为0,一个为1。
比如:
a: xxx0xx,
b: xxx1xx,
这样通过这一位去分组的话。就拿到两个数组,分别存在a和b。这两个数组的其他项不用担心,也一定是有重复,可以异或成0的。
如:
arr1: [a, 1, 1, 2, 2];
arr2: [b, 2, 2, 3, 3];
进一步理解,既然a的这一位为0(举例),那么数组中其他这一位 为0的就不可能是b。
那我怎么知道其他这些数字能两两成对呢?
因为这一位是0 的数字有一个满足的话,那和他相同的那个数字也能满足。就一定是成对出现的。(反证法了属于😂)
这样通过遍历arr1 的所有项就能获取a的值了。
获取b的值也可以复用刚才a^b 的结果。使a^b^a = b了;
至于怎么获取这一位变成 0001000,就看其他文章,本文不做讨论。
代码就不放了。思路最重要。
相关文章:
)
数组中只出现一次的两个数字(异或法思路)
题目简介 一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b 用HashMap记录就不说了。 这里记录一下用异或的方式解决。 由于异或特性为自己异或自己为0。a^a 0;所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉…...

python支持的操作系统有哪些
支持python开发环境的系统有Linux、OSX和windows,以及所有主要的操作系统中。 Linux,Linux系统是为编程而设计的,因此在大多数Linux计算机中,都默认安装了Python。编写和维护Linux的人认为会使用这种系统进行编程。要在Linux中运…...

S3C2440开发环境搭建
拿出了之前的S3C2440开发板,然后把移植uboot、移植内核、制作根文件系统、设备树编写驱动等几项再做一遍,这篇文章先记录下环境搭建过程,以及先把现成的uboot、内核、根文件系统下载进去,看看开发板还能不能用,先熟悉一…...

软件测试之测试用例
测试用例 1. 测试用例定义 测试用例又叫做test case,是为某个特殊目标而编制的一组测试输入、执行条件以及预期结果,以便测试某个程序路径或核实是否满足某个特定需求。 2. 编写测试用例的原因 2.1 理清思路,避免遗漏 如果测试的项目大而复杂&#…...

null和undefined的区别有哪些?
null和undefined的区别有哪些?相同点不同点undefinednull总结相同点 1.null和undefined都是js的基本数据类型 2.undefined和null都是假值(falsy),都能作为条件进行判断,所以在绝大多数情况下两者在使用上没有区别 if(undefined)…...

【强烈建议收藏:计算机网络面试专题:HTTP协议、HTTP请求报文和响应报文、HTTP请求报文常用字段、HTTP请求方法、HTTP响应码】
一.知识回顾 之前我们一起学习了HTTP1.0、HTTP1.1、HTTP2.0协议之前的区别、以及URL地址栏中输入网址到页面展示的全过程&&DNS域名解析的过程、HTTP协议基本概念以及通信过程、HTTPS基本概念、SSL加密原理、通信过程、中间人攻击问题、HTTP协议和HTTPS协议区别。接下来…...
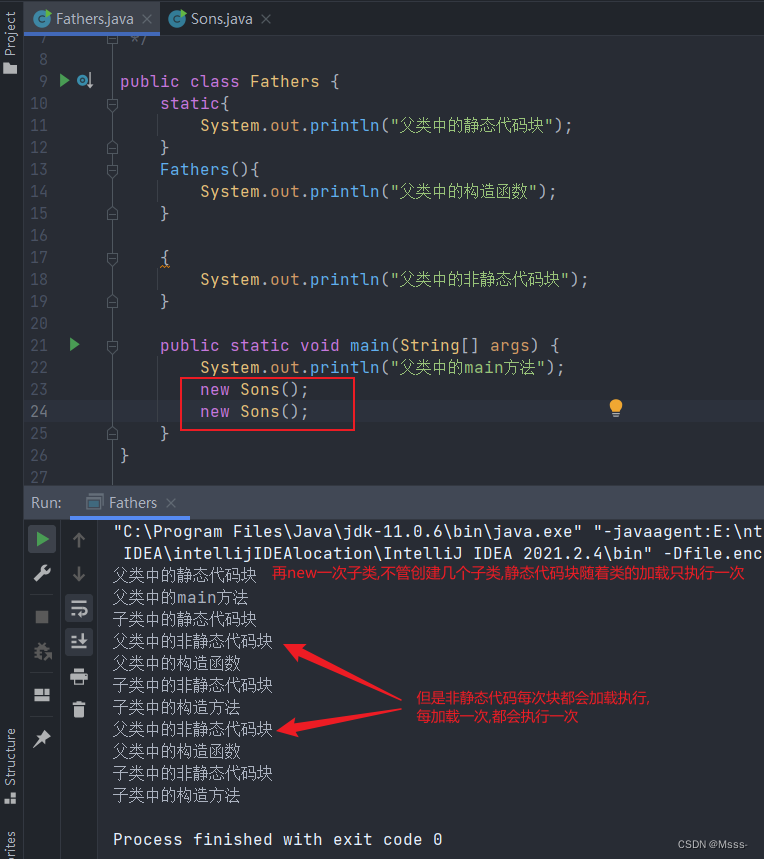
关于Java中的静态块讲解
文章目录类的加载特性与时机类加载的特性类加载的时机static的三个常用地方什么是静态块?特点写法静态块 static怎么用?类的加载特性与时机 在介绍static之前可以先看看类的相关 类加载的特性 在JVM的生命周期里,每个类只会被加载一次。 类加载的原则…...
ledcode【用队列实现栈】
目录 题目描述: 解析题目 代码解析 1.封装一个队列 1.2封装带两个队列的结构体 1.3封装指向队列的结构体 1.4入栈函数实现 1.5出栈函数实现 1.6取栈顶数据 1.7判空函数实现 题目描述: 解析题目 这个题我是用c语言写的,所以队列的pu…...

【基础算法】双指针----字符串删减
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Billu靶场黑盒盲打——思路和详解
一、信息收集 1、探测内网主机IP可以使用各种扫描工具比如nmap,我这里用的是自己编写的。 nmap -n 192.168.12.0/24 #扫描IP,发现目标主机 2、先不着急,先收集一波它的端口(无果) nmap -n 192.168.12.136 -p 1-10000…...

【2363. 合并相似的物品】
来源:力扣(LeetCode) 描述: 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,we…...
)
【C++提高编程】C++全栈体系(二十四)
C提高编程 第三章 STL - 常用容器 九、map/ multimap容器 1. map基本概念 简介: map中所有元素都是pairpair中第一个元素为key(键值),起到索引作用,第二个元素为value(实值)所有元素都会根…...
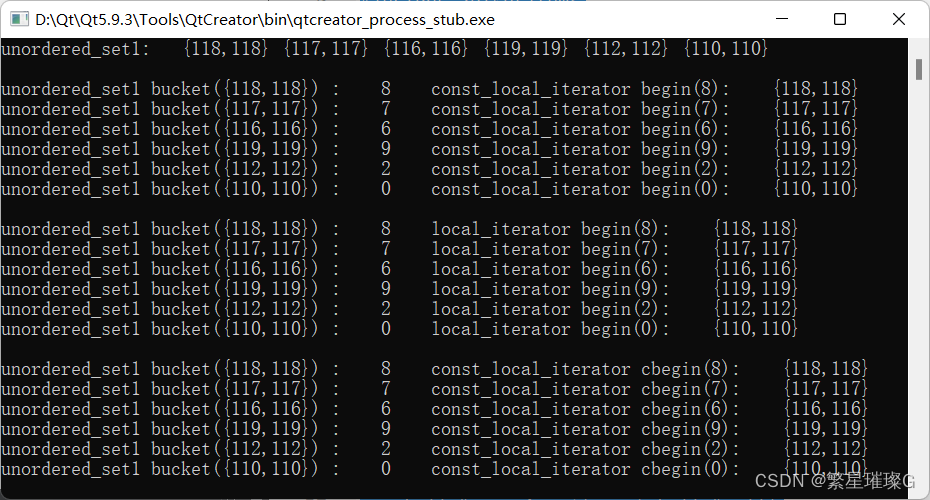
c++11 标准模板(STL)(std::unordered_set)(十一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点算法复习1、二叉树的遍历2、回溯算法3、二分搜索4、滑动窗口算法题5、经典动态规划6、动态规划答疑篇6.1、总结一下如何找到动态规划的状态转移关系7、编辑距离8、戳气球问题9、最长公共子序列 Longest Common Subsequence…...

华为OD机试题,用 Java 解【静态扫描最优成本】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
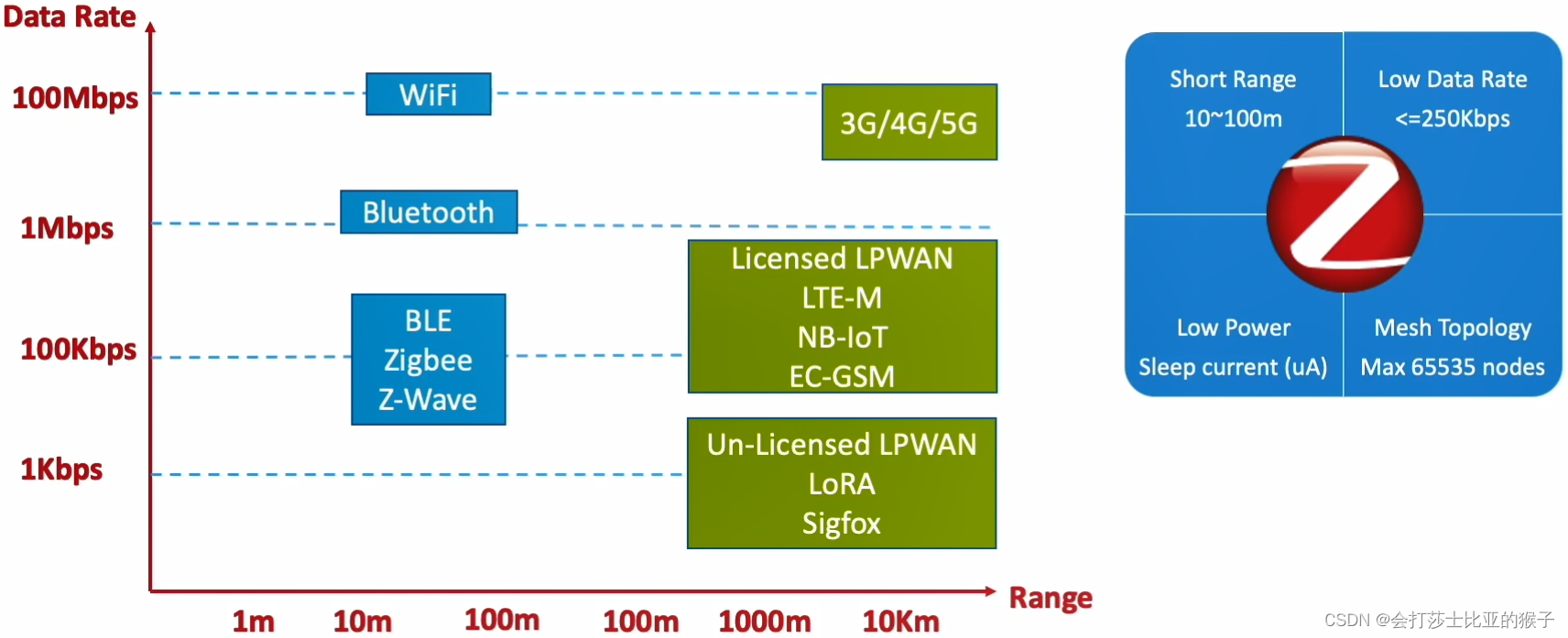
常见无线技术方案介绍
无线技术 无线网络大体有两种:WAN(广域网)、PAN(个人区域网)。 对于LoRa,NB-IoT,2G / 3G / 4G等无线技术,通常传输距离超过1 km,因此它们主要用于广域网(WA…...

收获满满的2022年
收到csdn官方的证书,感谢官方的认可!...

react的生命周期
目录 一、初始化阶段 constructor() static getDerivedStateFromProps() componentWillMount() / UNSAFE_componentWillMount() render(): componentDidMount() 二、运行阶段 componentWillUpdate() / UNSAFE_componentWillUpdate() render() getSnapsh…...

scanpy 单细胞分析API接口使用案例
参考:https://zhuanlan.zhihu.com/p/537206999 https://scanpy.readthedocs.io/en/stable/api.html scanpy python包主要分四个模块: 1)read 读写模块、 https://scanpy.readthedocs.io/en/stable/api.html#reading 2)pp Prepr…...

【Vue3 第二十一章】Teleport组件传送
一、基本使用场景 有时我们可能会遇到这样的场景:一个组件模板的一部分在逻辑上从属于该组件,但从整个应用视图的角度来看,它在 DOM 中应该被渲染在整个 Vue 应用外部的其他地方。 这类场景最常见的例子就是全屏的模态框。理想情况下&#…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
