AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点
- 算法复习
- 1、二叉树的遍历
- 2、回溯算法
- 3、二分搜索
- 4、滑动窗口算法题
- 5、经典动态规划
- 6、动态规划答疑篇
- 6.1、总结一下如何找到动态规划的状态转移关系
- 7、编辑距离
- 8、戳气球问题
- 9、最长公共子序列 Longest Common Subsequence
- 10、子序列的相关问题。最长,回文,编辑距离。
- 11、动态规划,博弈问题
- 12、贪心算法
- 13、二叉堆,实现优先级队列
- 14、LRU缓存淘汰策略
- 15、完全二叉树 满二叉树
本人参加了一些互联网大公司(N个公司)的笔试,机试以及后续的面试过程。主要总结一下在笔试和面试中的高频考点。主要是要掌握以下几类算法的核心思想。在笔试和面试的过程中,遇到这些问题,想清楚思路,然后套用下面的解法,将会非常有用。我没有刷500道LeetCode题,所以整体的刷题量和对事情的复杂程度还没有到位。但是下面的浅见,供大家参考一下。互相学习。祝福找工作的同学们,一切顺利。
算法复习
1、二叉树的遍历
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
前序遍历,中序遍历能够重构出后序遍历;
后序遍历,中序遍历能够重构出前序遍历;
前序遍历,后序遍历无法重构出中序遍历。
void traverse(TreeNode root){//前序遍历traverse(root.left);//中序遍历traverse(root.right);//后序遍历
}
2、回溯算法
def backtrack(...):for 选择 in 选择列表:做选择backtrack()撤销选择
路径,选择列表,结束条件
动态规划:状态,选择,base case 重叠子问题,可以用dp table或者备忘录 优化。
queue 先进先出。 stack 先进后出.
3、二分搜索
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只找到⼀个target 的索引即可
所以当 nums[mid] == target 时可以⽴即回
-
寻找左侧边界的二分查找
在nums[mid] == target时,
right=mid-1.
-
寻找右侧边界的二分查找
在nums[mid] == target时,
left=mid+1.
返回逻辑记得防止越界,边界检查。
4、滑动窗口算法题
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {unordered_map<char, int> need, window;for (char c : t) need[c]++;int left = 0, right = 0;int valid = 0; while (right < s.size()) {// c 是将移入窗口的字符char c = s[right];// 右移窗口right++;// 进行窗口内数据的一系列更新.../*** debug 输出的位置 ***/printf("window: [%d, %d)\n", left, right);/********************/// 判断左侧窗口是否要收缩while (window needs shrink) {// d 是将移出窗口的字符char d = s[left];// 左移窗口left++;// 进行窗口内数据的一系列更新...}}
}
5、经典动态规划
这个问题有什么「状态」,有什么「选择」,然后穷举。
对于高楼扔鸡蛋问题,状态:鸡蛋的个数。楼层的层数;随着测试的进行,K减少,楼层N减少。
选择:去哪层楼扔鸡蛋;线性扫描?二分法?等等。策略问题。
穷举加DP table。就可以解决动态规划的特性。 稍微处理一下 base case。
def dp(K, N):for 1 <= i <= N:# 最坏情况下的最少扔鸡蛋次数res = min(res, max( dp(K - 1, i - 1), # 碎了,就去低一层楼找;dp(K, N - i) # 没碎,就去高一层楼找。) + 1 # 在第 i 楼扔了一次)return res
对于动态规划的标准步骤:
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for …
dp[状态1] [状态2] […] = 择优(选择1,选择2…)
stack堆栈,先进后出。stack.top( )获取栈顶元素; stack.pop( ),删除栈顶元素; stack.push(5),推入元素到栈顶。
6、动态规划答疑篇
-
找最优子结构的过程:
其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。
最优子结构性质作为动态规划问题的必要条件,一定是让你求最值的。 从最简单的 base case 往后推导。
-
dp数组的遍历方向:
1、遍历的过程中,所需的状态必须是已经计算出来的。
2、遍历的终点必须是存储结果的那个位置。
6.1、总结一下如何找到动态规划的状态转移关系
1、明确 dp 数组所存数据的含义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
2、根据 dp 数组的定义,运用数学归纳法的思想,假设 dp[0...i-1] 都已知,想办法求出 dp[i],一旦这一步完成,整个题目基本就解决了。
但如果无法完成这一步,很可能就是 dp 数组的定义不够恰当,需要重新定义 dp 数组的含义;或者可能是 dp 数组存储的信息还不够,不足以推出下一步的答案,需要把 dp 数组扩大成二维数组甚至三维数组。
7、编辑距离
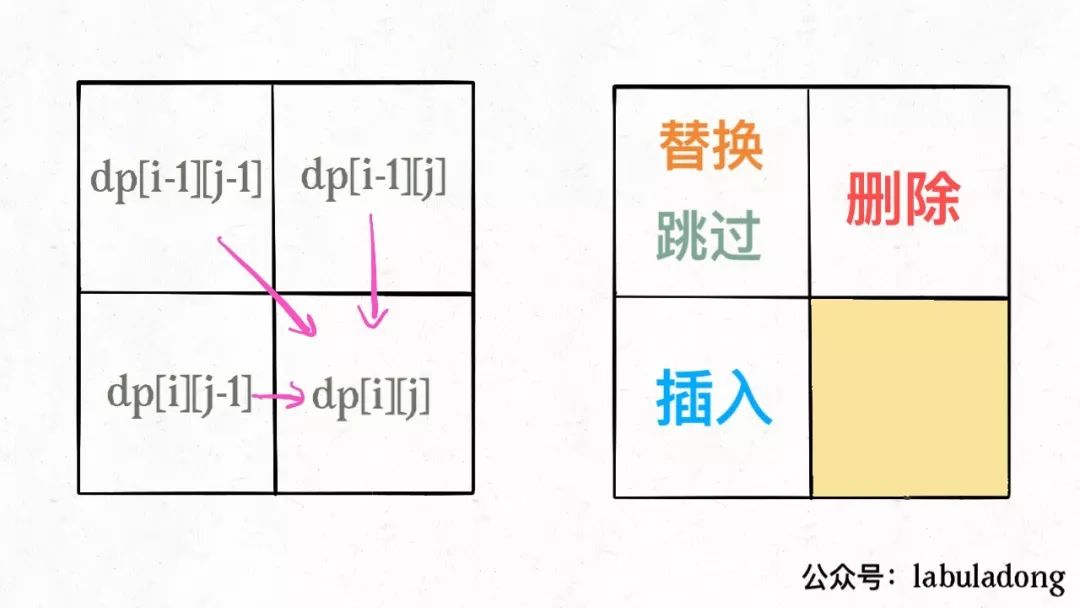
编辑距离的dp状态转移矩阵,比较巧妙。如何设计这个函数。左上,左边,上边。三个方向选最小的。跳转到[i+1] [j+1].
if s1[i] == s2[j]:
啥都别做(skip)
i, j 同时向前移动
else:
三选一:
插入(insert)
删除(delete)
替换(replace)
状态转移所依赖的状态必须被提前计算出来。
8、戳气球问题
这个问题中我们每戳破一个气球nums[i],得到的分数和该气球相邻的气球nums[i-1]和nums[i+1]是有相关性的。
这里面比较巧妙的是,如何转移矩阵。将气球🎈划分成不被破坏的,相互独立的3个子块。
dp[i] [k] + dp[k] [j] + points[i] * points[k] * points[j]
你不是要最后戳破气球k吗?那得先把开区间(i, k)的气球都戳破,再把开区间(k, j)的气球都戳破;最后剩下的气球k,相邻的就是气球i和气球j,这时候戳破k的话得到的分数就是points[i]*points[k]*points[j]。
9、最长公共子序列 Longest Common Subsequence
大部分比较困难的字符串问题,比如编辑距离,都是用二维动态规划来做。涉及到子序列问题,用动态规划来做。
子序列问题的核心。 dp 的转移。
从dp(i, j)转移到dp(i+1, j+1)。 字符串相同的时候,应该如何跳转,不同的时候,应该如何跳转。
关于状态转移,当s1[i]和s2[j]相同时不需要删除,不同时需要删除,所以可以利用dp函数计算两种情况,得出最优的结果。
| dp[i-1] [j-1] | dp[i-1] [j] |
|---|---|
| dp[i] [j-1] | dp[i] [j] |
10、子序列的相关问题。最长,回文,编辑距离。
涉及到子序列和最值,那几乎可以肯定,考察的是动态规划技巧,时间复杂度一般都是 O(n^2)。
然后根据实际问题看看哪种思路容易找到状态转移关系。
另外,找到状态转移和 base case 之后,一定要观察 DP table,看看怎么遍历才能保证通过已计算出来的结果解决新的问题
子序列问题,一共两种动态规划思路。二维的 dp 数组
-
涉及两个字符串/数组时(比如最长公共子序列),dp 数组的含义如下:
在子数组
arr1[0..i]和子数组arr2[0..j]中,我们要求的子序列(最长公共子序列)长度为dp[i][j]。第一种情况可以参考这两篇旧文:详解编辑距离和最长公共子序列 -
只涉及一个字符串/数组时(比如本文要讲的最长回文子序列),dp 数组的含义如下:
在子数组
array[i..j]中,我们要求的子序列(最长回文子序列)的长度为dp[i][j]。
if (s[i] == s[j])
// 它俩一定在最长回文子序列中
dp[i][j] = dp [ i + 1 ] [j - 1] + 2;
else
// s[i+1…j] 和 s[i…j-1] 谁的回文子序列更长?
dp[i][j] = max(dp [i + 1] [j], dp[i] [j - 1]);
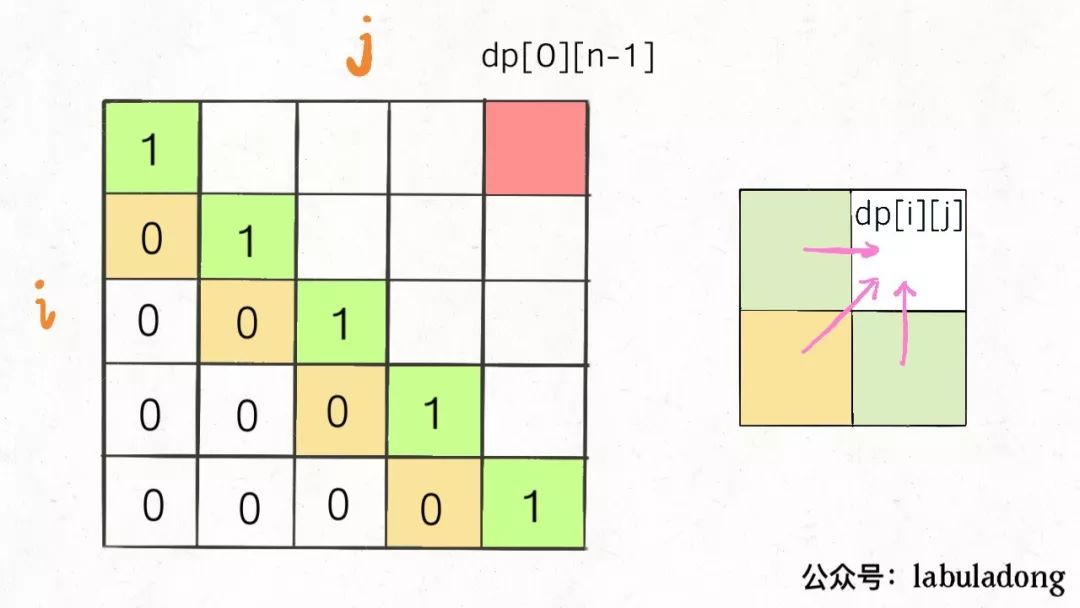
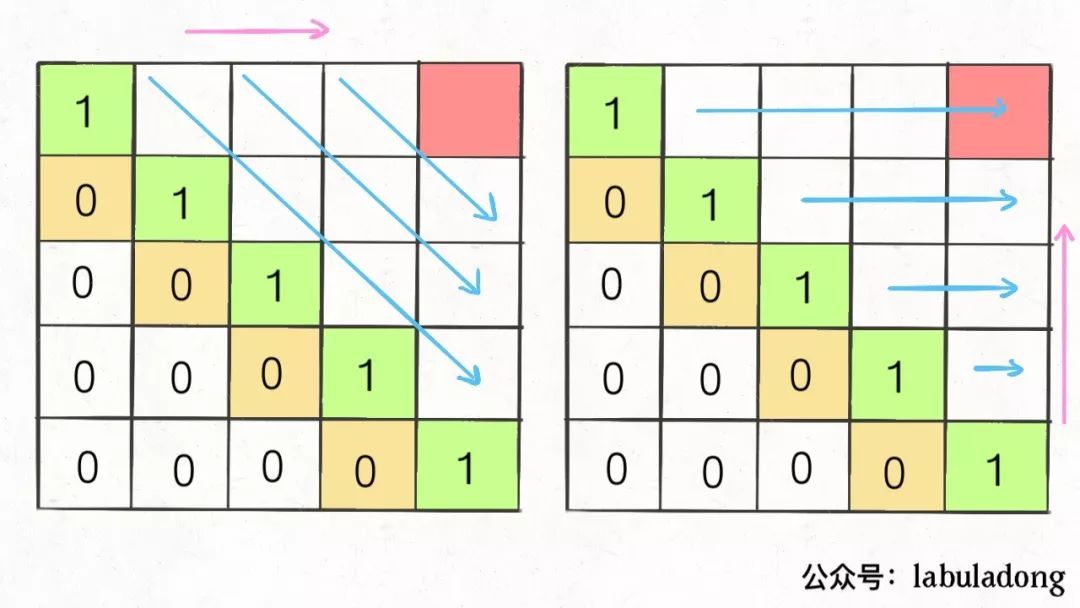
另外,看看刚才写的状态转移方程,想求dp[i][j]需要知道dp[i+1][j-1],dp[i+1][j],dp[i][j-1]这三个位置;再看看我们确定的 base case,填入 dp 数组之后是这样。为了保证每次计算dp[i][j],左、下、左下三个方向的位置已经被计算出来,只能斜着遍历或者反着遍历。
11、动态规划,博弈问题
博弈问题的前提一般都是在两个聪明人之间进行,编程描述这种游戏的一般方法是二维 dp 数组,数组中通过元组分别表示两人的最优决策。
之所以这样设计,是因为先手在做出选择之后,就成了后手,后手在对方做完选择后,就变成了先手。这种角色转换使得我们可以重用之前的结果,典型的动态规划标志。
12、贪心算法
对于区间问题的处理,一般来说第一步都是排序,相当于预处理降低后续操作难度。
13、二叉堆,实现优先级队列
Priority queue.
优先级队列,插入或者删除元素的时候,元素会自动排序,这底层的原理就是二叉堆的操作。
数据结构的功能无非增删查改,优先级队列有两个主要 API,分别是insert插入一个元素和delMax删除最大元素(如果底层用最小堆,那么就是delMin)。
insert方法先把要插入的元素添加到堆底的最后,然后让其上浮到正确位置。
delMax方法先把堆顶元素 A 和堆底最后的元素 B 对调,然后删除 A,最后让 B 下沉到正确位置。
优先级队列是基于⼆叉堆实现的,主要操作是插⼊和删除。插⼊是先插到最后,然后上浮到正确位置。删除操作是删除最大元素,先是交换位置到队尾,后再删除,然后将队列顶部的元素下沉到正确位置。核⼼代码也就⼗⾏。
删除是把第一个元素 pq[1](最值)调换到最后再删除,然后把新的 pq[1] 下沉到正确位置。
14、LRU缓存淘汰策略
LRU 缓存淘汰算法就是⼀种常⽤策略。LRU 的全称是 Least Recently Used,也就是 我们认为最近使⽤的数据应是「有⽤的」, 很久都没⽤过的数据应该是⽆⽤的,内存满了就优先删除很久没⽤的数据。
LRU 按访问时序淘汰缓存。还有LFU,按照访问频率淘汰。优先淘汰较少使用的应用/缓存。
LRU capacity作为容量,put(key,val)存入键值队,get(key)返回val。没有则-1。
注意
LRU缓存算法的核心是哈希链表,采用双向链表和哈希表结合。借助哈希表赋予了链表快速查找的特性。可以快速查找某个 key 是否存在缓存(链表)中,同时可以快速删除、添加节点。
为什么必须要⽤双向链表,因为我们需要删除操作。删除⼀个节点不光要得到该节点本⾝的指针,也需要操作其前驱节点的指针,⽽双向链表才能⽀持直接查找前驱,保证操作的时间复杂度O(1) 。
“为什么要在链表中同时存储 key 和 val,⽽不是只存储 val”,注意这段代码:
if (cap == cache.size()) {
// 删除链表最后⼀个数据
Node last = cache.removeLast();
map.remove(last.key);
}
当缓存容量已满,我们不仅仅要删除最后⼀个 Node 节点,还要把 map 中映射到该节点的 key 同时删除,⽽这个 key 只能由 Node 得到。如果 Node 结构中只存储 val,那么我们就⽆法得知 key 是什么,就⽆法删除 map 中的键,造成错误。
处理链表节点的同时不要忘了更新哈希表中对节点的映射。
链表操作,只需要处理指针。比较方便。
在二叉树框架上,扩展出一套BST遍历框架。
void BST(TreeNode root, int target)
{if (root.val == target)// 找到⽬标 做点什么if (root.val < target)BST(root.right, target);if (root.val > target)BST(root.left, target);
}
15、完全二叉树 满二叉树
完全二叉树如下图,每一层都是紧凑靠左排列的:
满二叉树如下图,是一种特殊的完全二叉树,每层都是是满的,像一个稳定的三角形。

\quad 完全二叉树 \quad \quad\quad\quad\quad\quad 满二叉树
一棵完全二叉树的两棵子树,至少有一棵是满二叉

算法的递归深度就是树的高度 O(logN),每次递归所花费的时间就是 while 循环,需要 O(logN),所以总体的时间复杂度是 O(logN*logN)。
相关文章:

AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点算法复习1、二叉树的遍历2、回溯算法3、二分搜索4、滑动窗口算法题5、经典动态规划6、动态规划答疑篇6.1、总结一下如何找到动态规划的状态转移关系7、编辑距离8、戳气球问题9、最长公共子序列 Longest Common Subsequence…...

华为OD机试题,用 Java 解【静态扫描最优成本】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
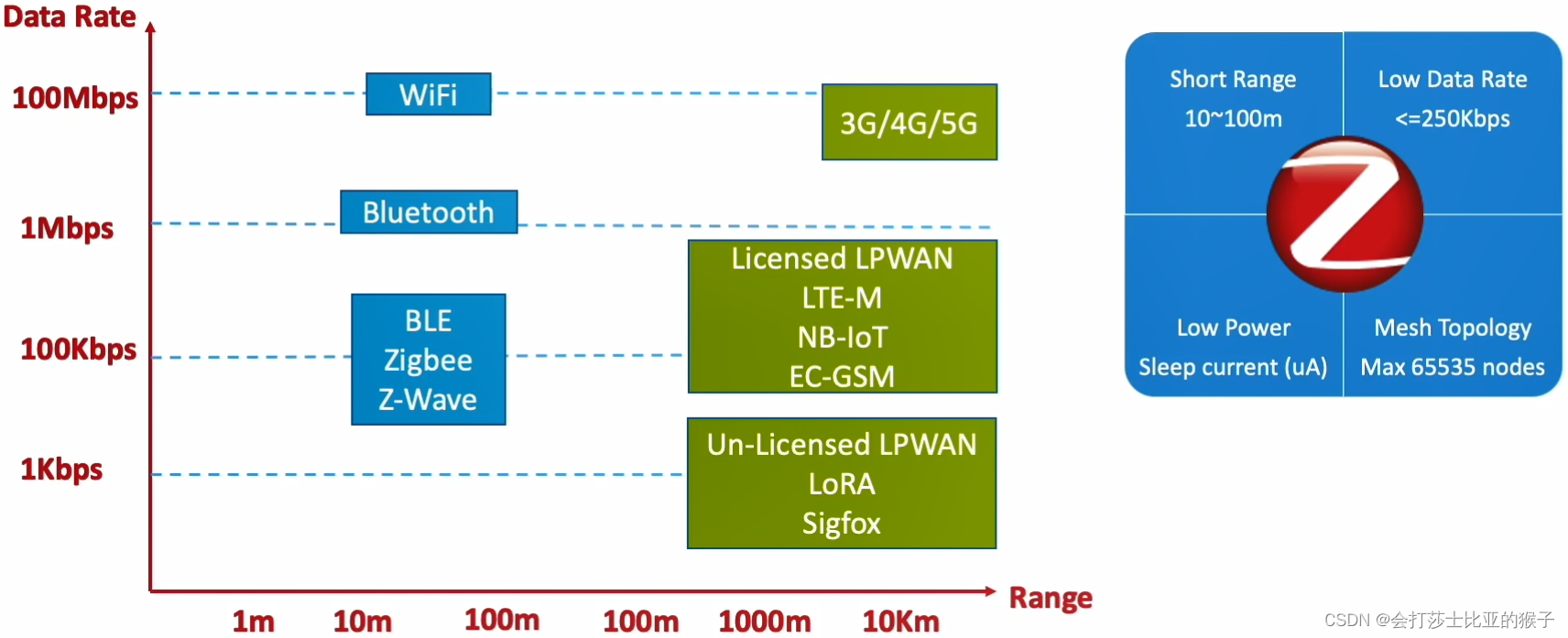
常见无线技术方案介绍
无线技术 无线网络大体有两种:WAN(广域网)、PAN(个人区域网)。 对于LoRa,NB-IoT,2G / 3G / 4G等无线技术,通常传输距离超过1 km,因此它们主要用于广域网(WA…...

收获满满的2022年
收到csdn官方的证书,感谢官方的认可!...

react的生命周期
目录 一、初始化阶段 constructor() static getDerivedStateFromProps() componentWillMount() / UNSAFE_componentWillMount() render(): componentDidMount() 二、运行阶段 componentWillUpdate() / UNSAFE_componentWillUpdate() render() getSnapsh…...

scanpy 单细胞分析API接口使用案例
参考:https://zhuanlan.zhihu.com/p/537206999 https://scanpy.readthedocs.io/en/stable/api.html scanpy python包主要分四个模块: 1)read 读写模块、 https://scanpy.readthedocs.io/en/stable/api.html#reading 2)pp Prepr…...

【Vue3 第二十一章】Teleport组件传送
一、基本使用场景 有时我们可能会遇到这样的场景:一个组件模板的一部分在逻辑上从属于该组件,但从整个应用视图的角度来看,它在 DOM 中应该被渲染在整个 Vue 应用外部的其他地方。 这类场景最常见的例子就是全屏的模态框。理想情况下&#…...

在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境
在 Windows Subsystem for Linux (WSL2) 的 Ubuntu 系统上配置 Vulkan 开发环境Vulkan Tutorial https://vulkan-tutorial.com/ Development environment - Linux https://vulkan-tutorial.com/Development_environment 1. Vulkan - Cross platform 3D Graphics https://www…...

放苹果HJ61
入门题目 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5&#…...

Windows下,OPC UA移植,open62541移植
OPC通信标准的核心是互通性 (Interoperability) 和标准化 (Standardization) 问题。传统的OPC技术在控制级别很好地解决了硬件设备间的互通性问题,在企业层面的通信标准化是同样需要的。OPC UA之前的访问规范都是基于微软的COM/DCOM技术, 这会给新增层面的通信带来不可根除的…...
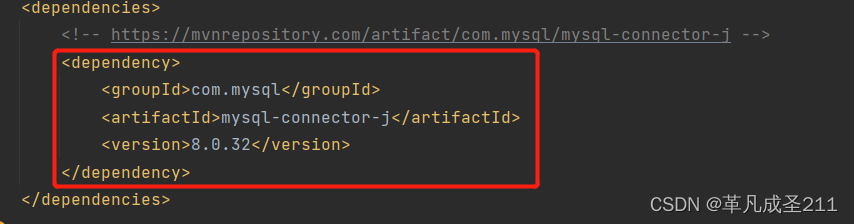
【Tomcat与Servlet篇1】认识Tomcat与Maven
目录 一、什么是Tomcat 二、Tomcat的几个重要目录 conf文件编辑 Server.xml logs文件 Webapps目录 三、如何使用Tomcat 但是,如果出现了点击之后进行闪退的情况,那又是怎么回事呢? 原因1:环境变量没有配置 原因2&#…...

C++类和对象:拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1.1 什么是拷贝构造函数 1.2 编译器默认生成的拷贝构造函数 1.3 拷贝构造函数特性总结 二. 运算符重载 2.1 运算符重载概述 2.2 比较运算符重载(> > < <) 2.2.1 >运算符的重载 2.2.2 运算符的重载 2.…...
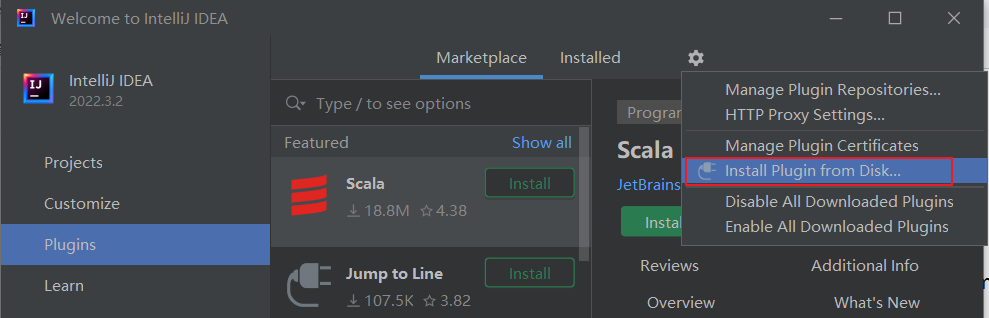
【IntelliJ IDEA】idea plugins搜索不出来,如何找到插件的解决方案
一、背景描述安装好IDEA后,想下载一些插件来使用,因为IDEA非常方便的一点就是插件使用非常的方便,但是经常会发现进入到插件市场无法搜索到插件的情况,这个时候就有点烦人了。那么怎么解决这个问题呢?以下会把我能想到…...

移动端自动化测试(一)appium环境搭建
自动化测试有主要有两个分类,接口自动化和ui自动化,ui自动化呢又分移动端的和web端的,当然还有c/s架构的,这种桌面程序应用的自动化,使用QTP,只不过现在没人做了。 web自动化呢,现在基本上都是…...
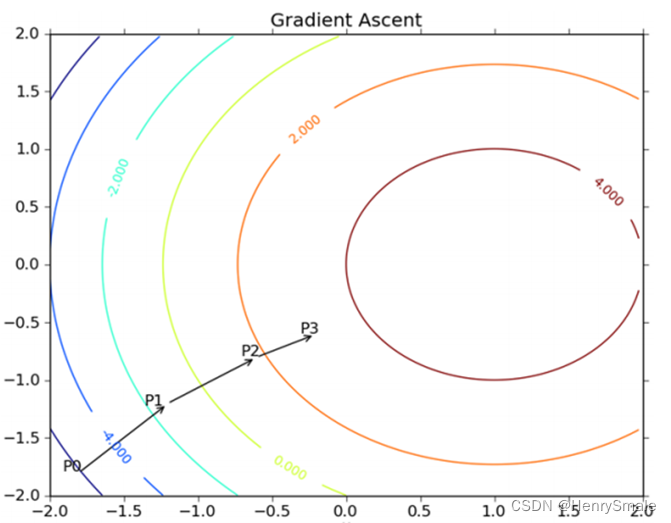
5 逻辑回归及Python实现
1 主要思想 分类就是分割数据: 两个条件属性:直线;三个条件属性:平面;更多条件属性:超平面。 使用数据: 5.1,3.5,0 4.9,3,0 4.7,3.2,0 4.6,3.1,0 5,3.6,0 5.4,3.9,0 . . . 6.2,2.9,1 5.1,2.5…...
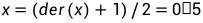
技术干货 | Modelica建模秘籍之状态变量
在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。图1 一只南美洲亚马…...

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

rollup环境配置
VUE2.x源码学习笔记 1. rollup环境配置 首先在VScode中新建文件夹vue_sc,然后终端打开定位到打开的文件夹,输入“npm init -y”初始化配置项,运行成功之后文件夹新增package.json文件 继续在终端运行"npm install babel/preset-env ba…...

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
