D. Moscow Gorillas(双指针 + 区间分析)
Problem - D - Codeforces
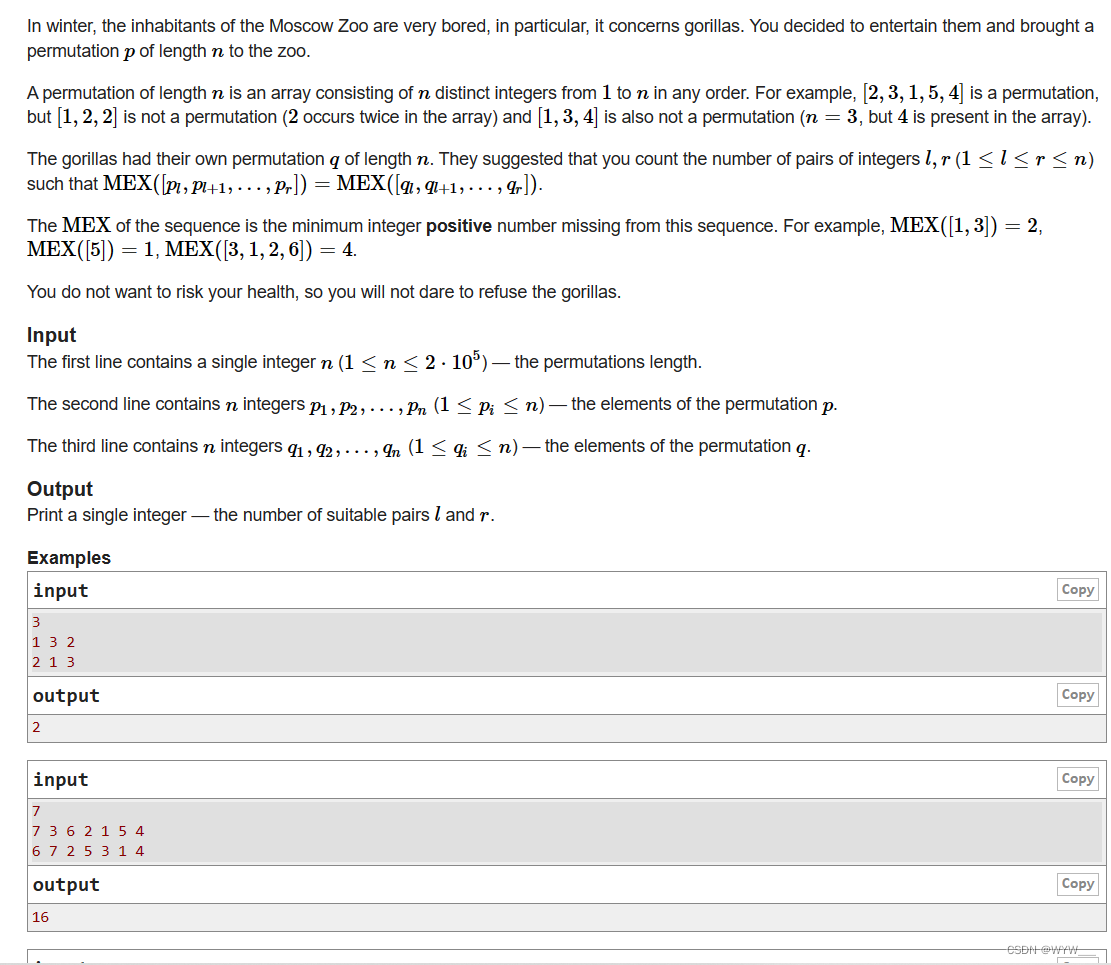
在冬天,莫斯科动物园的居民非常无聊,尤其是大猩猩。你决定娱乐他们,带了一个长度为n的排列p到动物园。长度为n的排列是由n个从1到n的不同整数以任意顺序组成的数组。例如,[2,3,1,5,4]是一个排列,但[1,2,2]不是一个排列(2在数组中出现两次),[1,3,4也不是一个排列(n3,但4在数组中出现)。大猩猩有自己的长度为n的排列q。他们建议你计算整数l,r (1 r n)对的数量,使得MEX([p1, Pl+1,,p,]) = MEX([a,9+1,,a])。数列的MEX是数列中缺少的最小正整数。例如,MEX([1,3]) = 2,MEX([5]) = 1, MEX([3,1,2,6]) = 4。你不想拿自己的健康冒险,所以你也不敢拒绝大猩猩。输入第一行包含一个整数n (1 <n<2.105)-排列长度。第二行包含n个整数p1 P2。,Pn (1 <pi Sn)-排列p的元素。第三行包含n个整数q1,92,,an (1 <gi Sn)-排列q的元素。输出打印一个整数-合适的对l和r的数量。
Examples
input
Copy
3
1 3 2
2 1 3
output
Copy
2
input
Copy
7
7 3 6 2 1 5 4
6 7 2 5 3 1 4
output
Copy
16
input
Copy
6
1 2 3 4 5 6
6 5 4 3 2 1
output
Copy
11
题解:
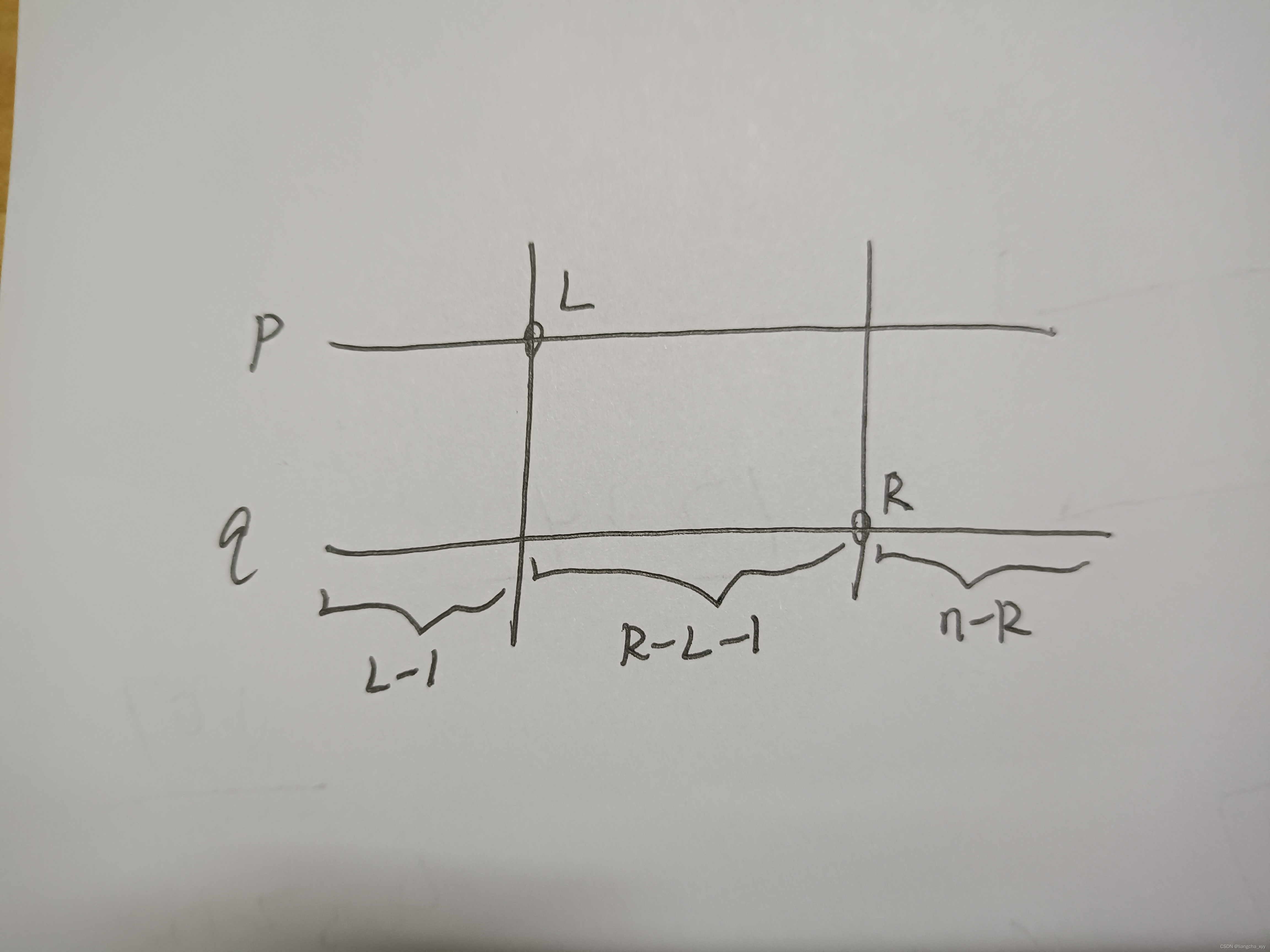
我们假设L,R分别是此时排列p,q1的位置,
那么MEX(1)l,r成立的情况有三种
1.均在L左侧
2.均在R右侧
3.在L,R之间
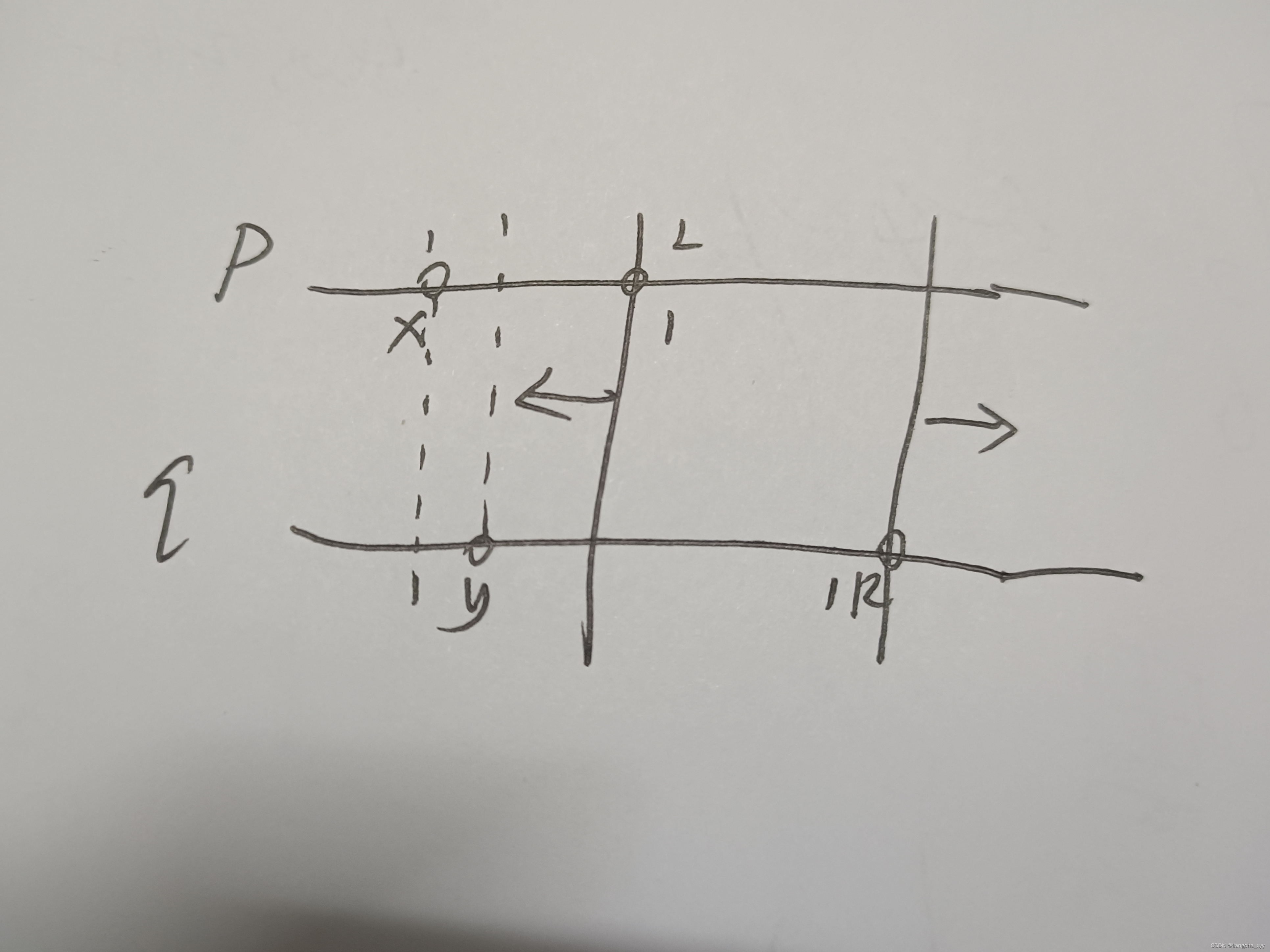
假设x,y是此时p,q排列的位置
接着考虑MEX = 2的情况。MEX = 2时,说明区间里一定包含1,但不含2,那么2的位置就不能出现在【L,R】之间。设x为序列p中2的位置,y为序列q中2的位置,x<=y, x,y要么同时出现在【1,L-1】一侧,要么同时出现在【R+1,n】一侧,要么一边在【1,L-1】一边在【R+1,n】。
成立的情况只有三种
1.都在L的左边 (L-y)*(n-R+1)
2.都在R的右边 L*(x-R)
3.x在L左边,y在R右边 (L-x)*(y-R)
随着MEX()增大,L,R区间会逐渐增大,或不变,所以要不断更新,
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
using namespace std;
#define int long long
const int N = 6e5 + 10;
int p[N],q[N];
int posp[N];
int posq[N];
int mod = 998244353;
int C(int n)
{return (n+1)*n/2;//区间l == r的情况也要算所以是n*(n-1)/2 + n
}
void solve()
{int n;cin >> n;int ans = 0; for(int i = 1;i <= n;i++){cin >> p[i];posp[p[i]] = i;}for(int i = 1;i <= n;i++){cin >> q[i];posq[q[i]] = i;}int L = posp[1];int R = posq[1];if(L > R)swap(L,R);ans += C(L-1);ans += C(max(0ll,R-L-1));ans += C(n - R);for(int i = 2;i <= n;i++){int x = posp[i];int y = posq[i];if(x > y)swap(x,y);if(y < L){ans += (L - y)*(n - R+1);}else if(x > R){ans += L*(x - R);}else if(x < L&&y > R){ans += (L - x)*(y - R);}L = min(L,x);R = max(R,y);}cout << ans + 1;//+1是整个排列都算一种
}
signed main()
{int t = 1;
// cin >> t;while(t--){solve();}
}相关文章:
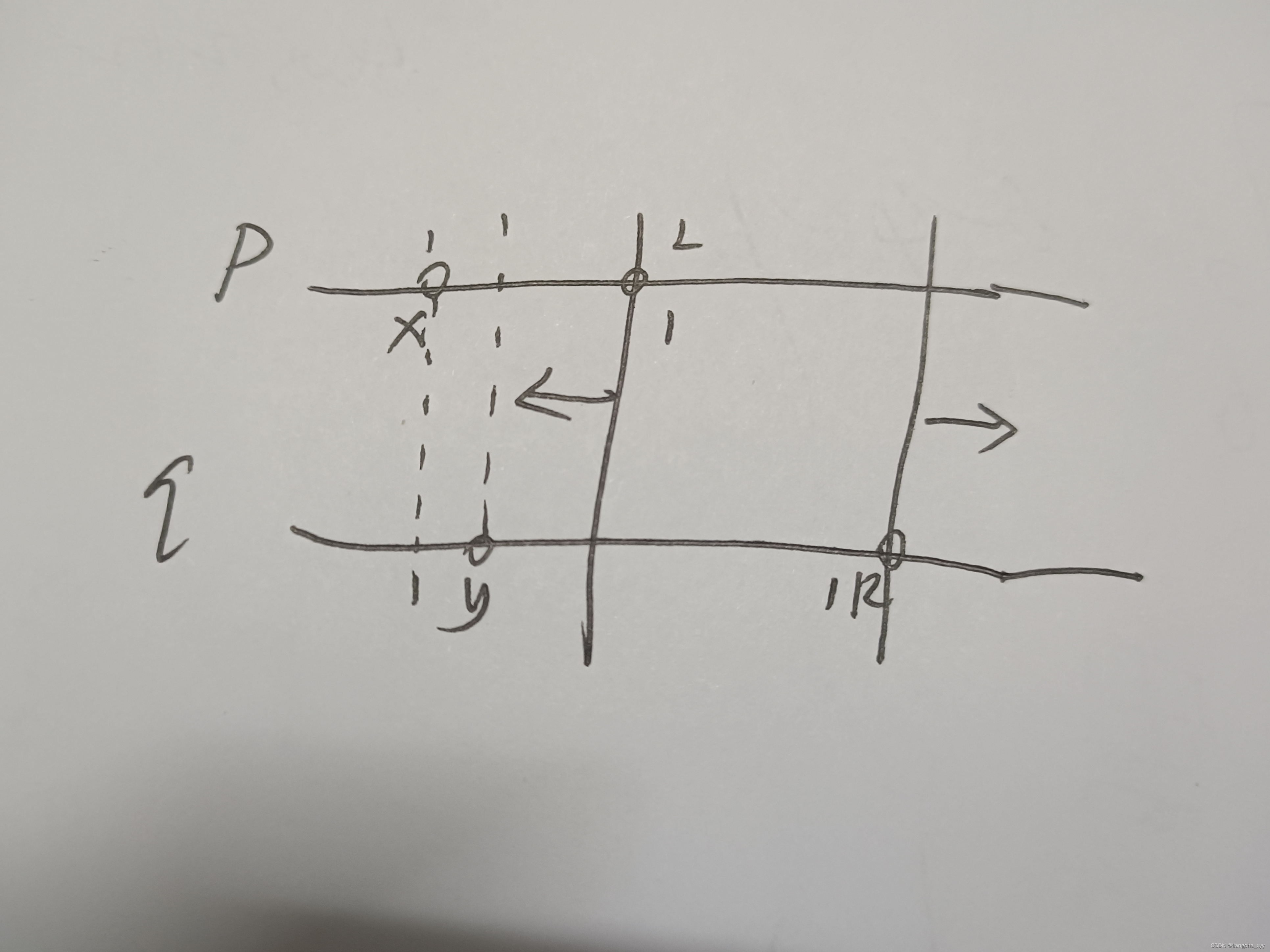
D. Moscow Gorillas(双指针 + 区间分析)
Problem - D - Codeforces 在冬天,莫斯科动物园的居民非常无聊,尤其是大猩猩。你决定娱乐他们,带了一个长度为n的排列p到动物园。长度为n的排列是由n个从1到n的不同整数以任意顺序组成的数组。例如,[2,3,1,5,4]是一个排列…...

华为OD机试题,用 Java 解【相同数字的积木游戏 1】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

Python实现GWO智能灰狼优化算法优化BP神经网络分类模型(BP神经网络分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。1.项目背景灰狼优化算法(GWO),由澳大利亚格里菲斯大学学者 Mirjalili 等人于2014年提出来的一种群智能优…...

无线蓝牙耳机哪个牌子好?2023质量好的无线蓝牙耳机推荐
近几年,随着蓝牙技术的不断进步,使用蓝牙耳机的人也越来越多。蓝牙耳机的出现,不仅能让我们摆脱线带来的约束,还能提升我们学习和工作的效率。最近看到很多人问,无线蓝牙耳机哪个牌子好?下面,我…...

Qt之QTableView自定义排序/过滤(QSortFilterProxyModel实现,含源码+注释)
一、效果示例图 1.1 自定义表格排序示例图 本文过滤条件为行索引取余2等于0时返回true,且从下图中可以看到,奇偶行是各自挨在一起的。 1.2 自定义表格过滤示例图 下图添加两列条件(当前数据大于当前列条件才返回true,且多个列…...
电商(强一致性系统)的场景设计
领域拆分:如何合理地拆分系统? 一般来说,强一致性的系统都会牵扯到“锁争抢”等技术点,有较大的性能瓶颈,而电商时常做秒杀活动,这对系统的要求更高。业内在对电商系统做改造时,通常会从三个方面…...
)
算法与数据结构(一)
一、时间复杂度 一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。 时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多…...

【Python】元组如何创建?
嗨害大家好鸭!我是小熊猫~ Python 元组 Python 的元组与列表类似, 不同之处在于元组的元素不能修改。 元组使用小括号,列表使用方括号。 元组创建很简单,只需要在括号中添加元素, 并使用逗号隔开即可。 如下实例…...

qt操作文件以及字符串转换
//从文件加载英文属性与中文属性对照表QFile file(":/propertyname.txt");if (file.open(QFile::ReadOnly)) {//QTextStream方法读取速度至少快百分之30#if 0while(!file.atEnd()) {QString line file.readLine();appendName(line);}#elseQTextStream in(&file)…...
)
数组中只出现一次的两个数字(异或法思路)
题目简介 一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b 用HashMap记录就不说了。 这里记录一下用异或的方式解决。 由于异或特性为自己异或自己为0。a^a 0;所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉…...

python支持的操作系统有哪些
支持python开发环境的系统有Linux、OSX和windows,以及所有主要的操作系统中。 Linux,Linux系统是为编程而设计的,因此在大多数Linux计算机中,都默认安装了Python。编写和维护Linux的人认为会使用这种系统进行编程。要在Linux中运…...

S3C2440开发环境搭建
拿出了之前的S3C2440开发板,然后把移植uboot、移植内核、制作根文件系统、设备树编写驱动等几项再做一遍,这篇文章先记录下环境搭建过程,以及先把现成的uboot、内核、根文件系统下载进去,看看开发板还能不能用,先熟悉一…...

软件测试之测试用例
测试用例 1. 测试用例定义 测试用例又叫做test case,是为某个特殊目标而编制的一组测试输入、执行条件以及预期结果,以便测试某个程序路径或核实是否满足某个特定需求。 2. 编写测试用例的原因 2.1 理清思路,避免遗漏 如果测试的项目大而复杂&#…...

null和undefined的区别有哪些?
null和undefined的区别有哪些?相同点不同点undefinednull总结相同点 1.null和undefined都是js的基本数据类型 2.undefined和null都是假值(falsy),都能作为条件进行判断,所以在绝大多数情况下两者在使用上没有区别 if(undefined)…...

【强烈建议收藏:计算机网络面试专题:HTTP协议、HTTP请求报文和响应报文、HTTP请求报文常用字段、HTTP请求方法、HTTP响应码】
一.知识回顾 之前我们一起学习了HTTP1.0、HTTP1.1、HTTP2.0协议之前的区别、以及URL地址栏中输入网址到页面展示的全过程&&DNS域名解析的过程、HTTP协议基本概念以及通信过程、HTTPS基本概念、SSL加密原理、通信过程、中间人攻击问题、HTTP协议和HTTPS协议区别。接下来…...
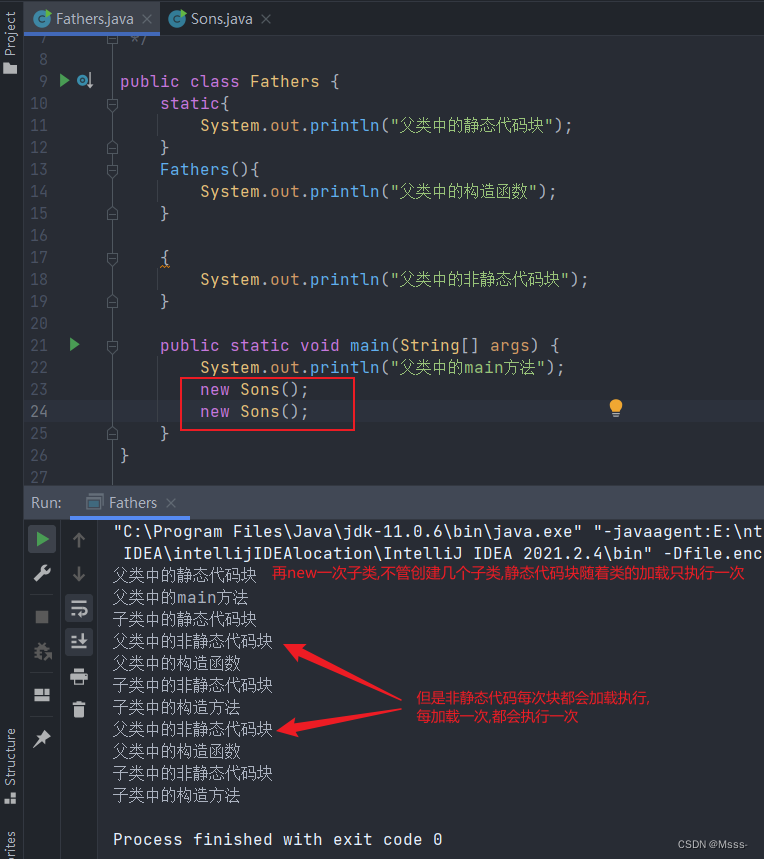
关于Java中的静态块讲解
文章目录类的加载特性与时机类加载的特性类加载的时机static的三个常用地方什么是静态块?特点写法静态块 static怎么用?类的加载特性与时机 在介绍static之前可以先看看类的相关 类加载的特性 在JVM的生命周期里,每个类只会被加载一次。 类加载的原则…...
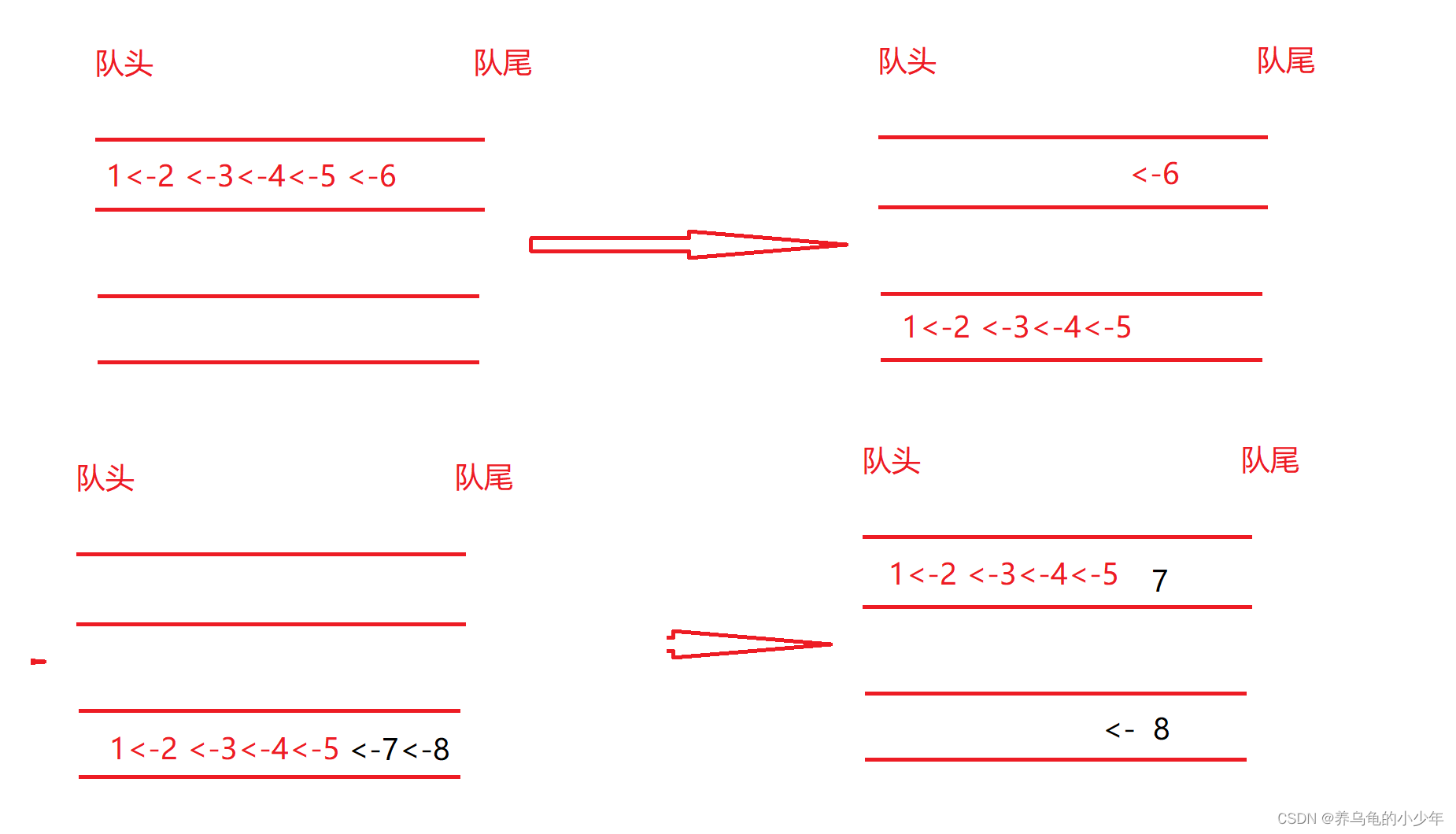
ledcode【用队列实现栈】
目录 题目描述: 解析题目 代码解析 1.封装一个队列 1.2封装带两个队列的结构体 1.3封装指向队列的结构体 1.4入栈函数实现 1.5出栈函数实现 1.6取栈顶数据 1.7判空函数实现 题目描述: 解析题目 这个题我是用c语言写的,所以队列的pu…...

【基础算法】双指针----字符串删减
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Billu靶场黑盒盲打——思路和详解
一、信息收集 1、探测内网主机IP可以使用各种扫描工具比如nmap,我这里用的是自己编写的。 nmap -n 192.168.12.0/24 #扫描IP,发现目标主机 2、先不着急,先收集一波它的端口(无果) nmap -n 192.168.12.136 -p 1-10000…...

【2363. 合并相似的物品】
来源:力扣(LeetCode) 描述: 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,we…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
