算法与数据结构(一)
一、时间复杂度
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
选择排序、冒泡排序的时间复杂度为O(N2)O(N^2)O(N2),额外空间复杂度为O(1)O(1)O(1)
c++实现的选择排序算法:
//创建一个数组int arr[] = {1, 6, 3, 6, 8, 6, 4};//判断数组是否为空或者只有一个数组if (arr == NULL || sizeof(arr) < 2){return;}//开始选择排序for (int i = 0; i < sizeof(arr)/sizeof(arr[0]) - 1; i++){// 暂存最小的数据下标索引int min = i;//从第一个操作数开始筛选for (int j = i + 1; j < sizeof(arr) / sizeof(arr[0]); j++){if (arr[min] > arr[j]){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}}}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
冒泡排序:
//创建数组int arr[] = { 2, 3, 5, 1, 3, 4, 5 };//判断数组是否为空或者只有一个数组if (arr == NULL || sizeof(arr) < 2){return;}//开始冒泡排序for (int i = sizeof(arr) / sizeof(arr[0]) - 1; i > 0; i--){for (int j = 0; j < i; j++){if (arr[j] > arr[j+1]){arr[i] = arr[j] ^ arr[i];arr[j] = arr[j] ^ arr[i];arr[i] = arr[j] ^ arr[i];}}}//输出排序后的数组for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
以上两种排序算法不管数组内部是什么情况,都需要执行固定的操作,但是插入排序要考虑数组内部的情况,在最好情况下(数组刚好按照想要排序的顺序排列),其时间复杂度为O(N)O(N)O(N),,最差情况下((数组刚好与想要排序的顺序相反)),其时间复杂度为O(N2)O(N^2)O(N2),在时间复杂度的考量上,以最差情况为标准,所以为O(N2)O(N^2)O(N2),其c++实现:
//创建数组int arr[] = { 2, 2, 3, 1, 3, 1, 5, 6 };//如果数组为空或者只有一个数据时,跳过if (arr == NULL || sizeof(arr) < 2){return;}//外侧循环for (int i = 1; i < sizeof(arr)/ sizeof(arr[0]); i++){//内侧循环for (int j = i; j > 0; j--){//如果内测循环指针指向的数据比左侧数据小,则进行交换if (arr[j - 1] > arr[j]){int tem = arr[j];arr[j] = arr[j - 1];arr[j - 1] = tem;}}}//输出排序后的数组for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){cout << arr[i] << " ";}cout << endl;
二、力扣刷题:
有一系列数组,只有一个数字出现了奇数次,其余的数出现了偶数次,求出出现奇数次的数据,要求算法的时间复杂度为O(N):
void test10()
{//创建一系列数组int arr[] = { 2, 2, 3, 1, 3, 1, 5 };int eor = 0;for (int i = 0; i < sizeof(arr)/sizeof(arr[0]); i++){//使用初始变量0逐个异或数组中的每一个元素eor ^= arr[i];}cout << "出现奇数次的数字为: " << eor << endl;
}在异或操作中,0异或0就会出现0的结果,1异或1就等于0,1异或0就等于1。异或操作也可以看成二进制的无进位相加。所以当数组中出现偶数个相同的元素时,其结果会是0,由于异或操作有交换性质,当0异或一个奇数个元素时,其结果就是该数。
有一系列数组,有两个数字出现了奇数次,且这两个奇数次的元素不相等,其余的数出现了偶数次,求出出现奇数次的数据,要求算法的时间复杂度为O(N):
//创建一系列数组int arr[] = { 2, 2, 3, 1, 3, 1, 5, 6 };int eor = 0;int eor1 = 0;for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//最终得出a异或b的结果eor ^= arr[i];}//提取eor二进制中的最后一个1int RightOne = eor & (~eor + 1);for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){if ((RightOne & arr[i]) == 0){//得出两个奇数次数数字之一eor1 ^= arr[i];}}cout << eor1 << (eor1 ^ eor) << endl;
假设两个出现奇数次的数分别为a,b。这道算法题与之前的算法题有相同之处,但是第一次遍历异或的结果是a异或b。我们只需要知道a或者b再异或一下a异或b的结果就可以得到另一个数字的结果。我们可以这样假设,因为a与b不相等,a异或b的结果也就肯定不为0。在二进制中,a异或b的结果肯定某一位会出现1。假设a异或b的结果为1010。在这里我们只看其中的一位,也就是第二位。a异或b在第二位中出现1,反映到a,b上我们可以知道。a或者b肯定在第二位为1,在这里我们假设a在第二位为1。我们只需要再次迭代一下数组中的元素,可以通过与的操作将第二位上不是1的数进行过滤,如果第二位上是1,我们只需要进行一个异或操作即可,因为除了a之外,其余第二位上是1的数都是偶数,所以最后异或出来的数就是a,再用a异或(a异或b)的结果可以得出b。
相关文章:
)
算法与数据结构(一)
一、时间复杂度 一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。 时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,这个算法流程中,发生了多…...

【Python】元组如何创建?
嗨害大家好鸭!我是小熊猫~ Python 元组 Python 的元组与列表类似, 不同之处在于元组的元素不能修改。 元组使用小括号,列表使用方括号。 元组创建很简单,只需要在括号中添加元素, 并使用逗号隔开即可。 如下实例…...

qt操作文件以及字符串转换
//从文件加载英文属性与中文属性对照表QFile file(":/propertyname.txt");if (file.open(QFile::ReadOnly)) {//QTextStream方法读取速度至少快百分之30#if 0while(!file.atEnd()) {QString line file.readLine();appendName(line);}#elseQTextStream in(&file)…...
)
数组中只出现一次的两个数字(异或法思路)
题目简介 一个数组中只有2个数字只有一个,其他数字都有两个。找出这两个数字。a, b 用HashMap记录就不说了。 这里记录一下用异或的方式解决。 由于异或特性为自己异或自己为0。a^a 0;所以可以异或数组中的所有数字得出 a^b 的结果,其他相同的都消掉…...

python支持的操作系统有哪些
支持python开发环境的系统有Linux、OSX和windows,以及所有主要的操作系统中。 Linux,Linux系统是为编程而设计的,因此在大多数Linux计算机中,都默认安装了Python。编写和维护Linux的人认为会使用这种系统进行编程。要在Linux中运…...

S3C2440开发环境搭建
拿出了之前的S3C2440开发板,然后把移植uboot、移植内核、制作根文件系统、设备树编写驱动等几项再做一遍,这篇文章先记录下环境搭建过程,以及先把现成的uboot、内核、根文件系统下载进去,看看开发板还能不能用,先熟悉一…...

软件测试之测试用例
测试用例 1. 测试用例定义 测试用例又叫做test case,是为某个特殊目标而编制的一组测试输入、执行条件以及预期结果,以便测试某个程序路径或核实是否满足某个特定需求。 2. 编写测试用例的原因 2.1 理清思路,避免遗漏 如果测试的项目大而复杂&#…...

null和undefined的区别有哪些?
null和undefined的区别有哪些?相同点不同点undefinednull总结相同点 1.null和undefined都是js的基本数据类型 2.undefined和null都是假值(falsy),都能作为条件进行判断,所以在绝大多数情况下两者在使用上没有区别 if(undefined)…...

【强烈建议收藏:计算机网络面试专题:HTTP协议、HTTP请求报文和响应报文、HTTP请求报文常用字段、HTTP请求方法、HTTP响应码】
一.知识回顾 之前我们一起学习了HTTP1.0、HTTP1.1、HTTP2.0协议之前的区别、以及URL地址栏中输入网址到页面展示的全过程&&DNS域名解析的过程、HTTP协议基本概念以及通信过程、HTTPS基本概念、SSL加密原理、通信过程、中间人攻击问题、HTTP协议和HTTPS协议区别。接下来…...
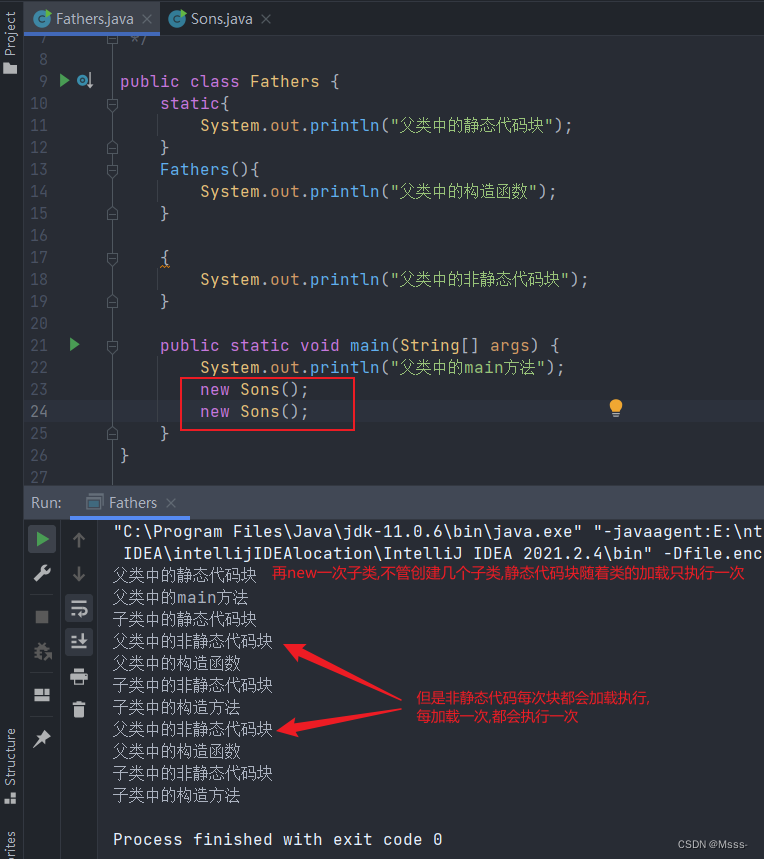
关于Java中的静态块讲解
文章目录类的加载特性与时机类加载的特性类加载的时机static的三个常用地方什么是静态块?特点写法静态块 static怎么用?类的加载特性与时机 在介绍static之前可以先看看类的相关 类加载的特性 在JVM的生命周期里,每个类只会被加载一次。 类加载的原则…...
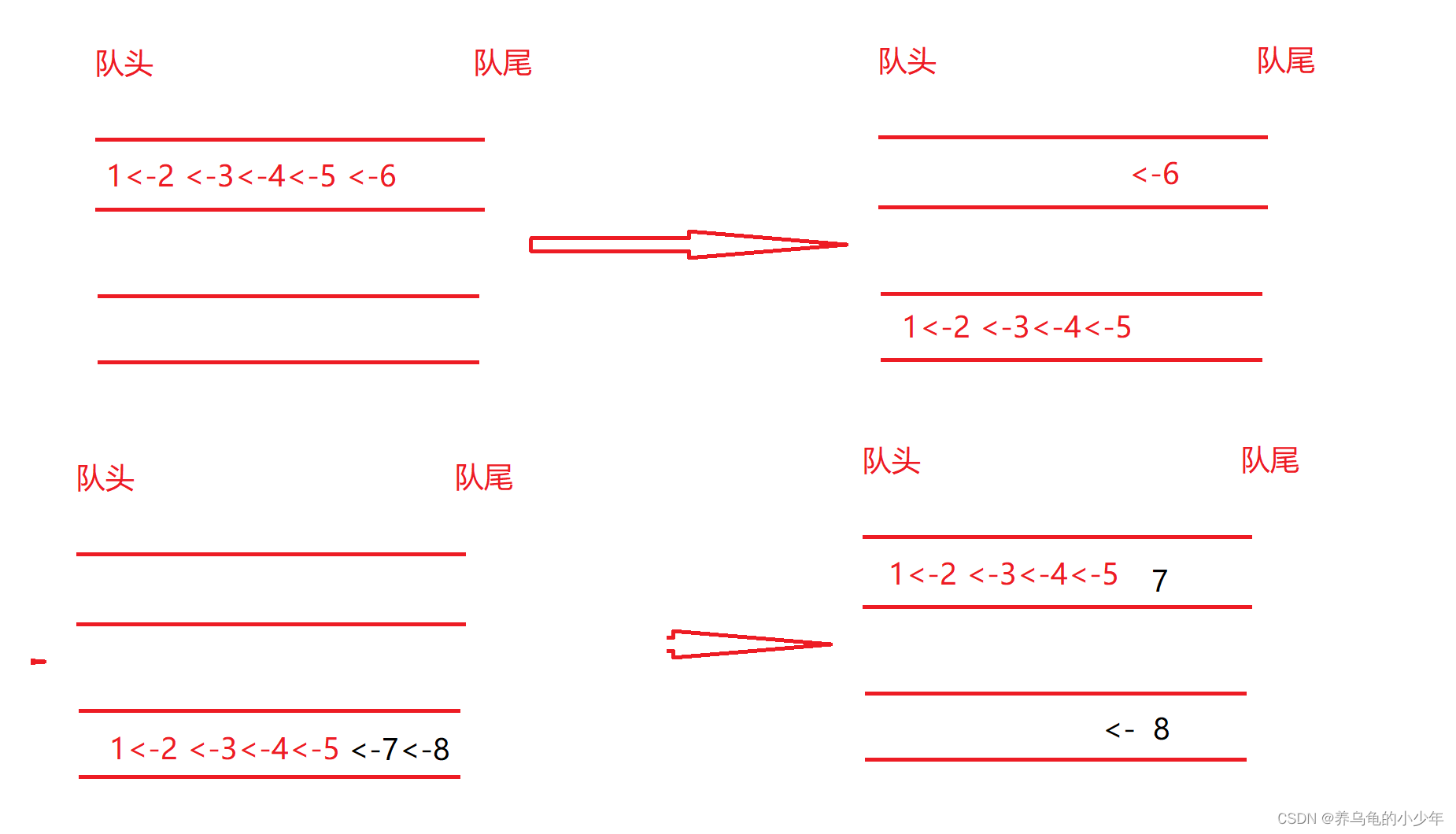
ledcode【用队列实现栈】
目录 题目描述: 解析题目 代码解析 1.封装一个队列 1.2封装带两个队列的结构体 1.3封装指向队列的结构体 1.4入栈函数实现 1.5出栈函数实现 1.6取栈顶数据 1.7判空函数实现 题目描述: 解析题目 这个题我是用c语言写的,所以队列的pu…...

【基础算法】双指针----字符串删减
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Billu靶场黑盒盲打——思路和详解
一、信息收集 1、探测内网主机IP可以使用各种扫描工具比如nmap,我这里用的是自己编写的。 nmap -n 192.168.12.0/24 #扫描IP,发现目标主机 2、先不着急,先收集一波它的端口(无果) nmap -n 192.168.12.136 -p 1-10000…...

【2363. 合并相似的物品】
来源:力扣(LeetCode) 描述: 给你两个二维整数数组 items1 和 items2 ,表示两个物品集合。每个数组 items 有以下特质: items[i] [valuei, weighti] 其中 valuei 表示第 i 件物品的 价值 ,we…...
)
【C++提高编程】C++全栈体系(二十四)
C提高编程 第三章 STL - 常用容器 九、map/ multimap容器 1. map基本概念 简介: map中所有元素都是pairpair中第一个元素为key(键值),起到索引作用,第二个元素为value(实值)所有元素都会根…...
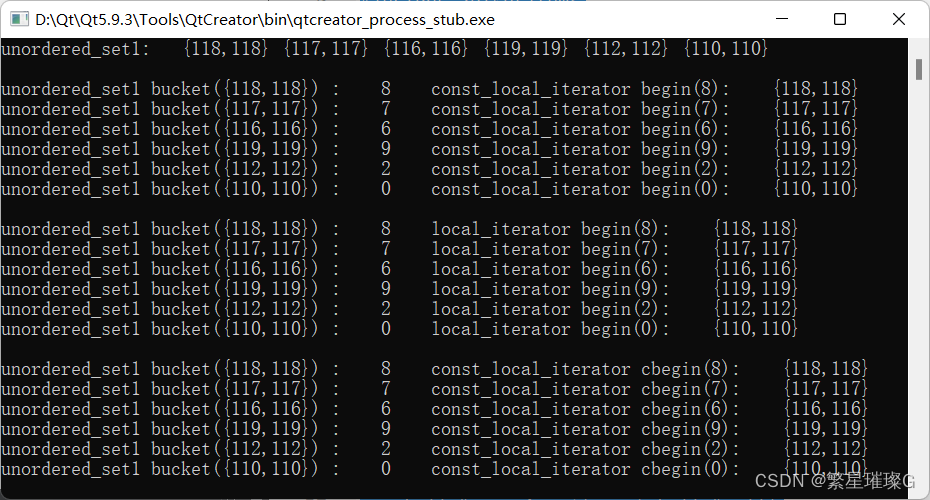
c++11 标准模板(STL)(std::unordered_set)(十一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

AI/CV大厂笔试LeetCode高频考题之基础核心知识点
AI/CV互联网大厂笔试LeetCode高频考题之基础核心知识点算法复习1、二叉树的遍历2、回溯算法3、二分搜索4、滑动窗口算法题5、经典动态规划6、动态规划答疑篇6.1、总结一下如何找到动态规划的状态转移关系7、编辑距离8、戳气球问题9、最长公共子序列 Longest Common Subsequence…...

华为OD机试题,用 Java 解【静态扫描最优成本】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
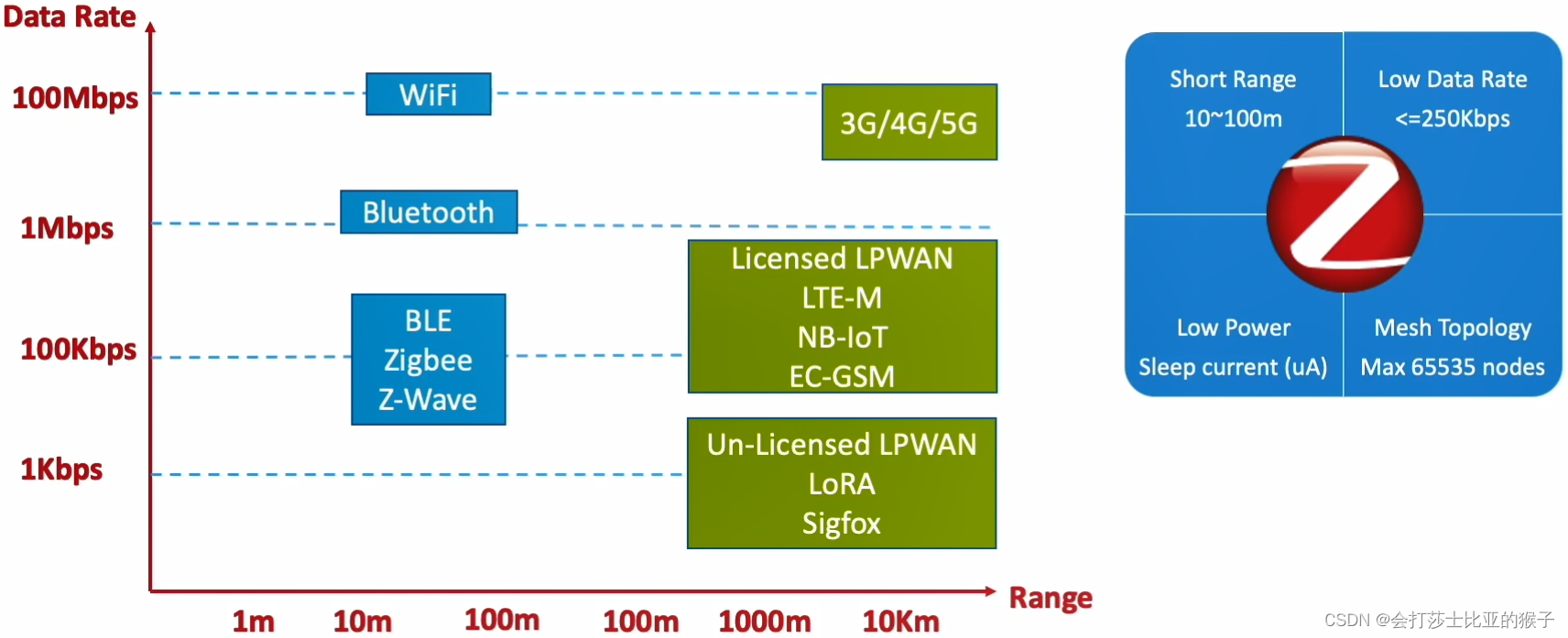
常见无线技术方案介绍
无线技术 无线网络大体有两种:WAN(广域网)、PAN(个人区域网)。 对于LoRa,NB-IoT,2G / 3G / 4G等无线技术,通常传输距离超过1 km,因此它们主要用于广域网(WA…...

收获满满的2022年
收到csdn官方的证书,感谢官方的认可!...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
