scipy实现单因素方差分析
经典例题
某校高二年级共有四个班,采用四种不同的教学方法进行数学教学,为了比较这四种教学法的效果是否存在明显的差异,期末统考后,从这四个班中各抽取 5 名考生的成绩,如下所示。
| 班级 | 一班 | 二班 | 三班 | 四班 | |
| 1 | 75 | 93 | 65 | 72 | |
| 2 | 77 | 80 | 67 | 70 | |
| 3 | 70 | 85 | 77 | 71 | |
| 4 | 88 | 90 | 68 | 65 | |
| 5 | 72 | 84 | 65 | 81 | |
| 6 | 80 | 86 | 64 | 72 | |
| 7 | 79 | 85 | 62 | 68 | |
| 8 | 81 | 81 | 68 | 74 |
问这四种教学法的效果是否存在显著性差异(α =0.05)?
1.计算F值
import numpy as np
from scipy.stats import f_oneway# Data for the four classes
class1 = [75, 77, 70, 88, 72, 80, 79, 81]
class2 = [93, 80, 85, 90, 84, 86, 85, 81]
class3 = [65, 67, 77, 68, 65, 64, 62, 68]
class4 = [72, 70, 71, 65, 81, 72, 68, 74]# Perform one-way ANOVA
f_statistic, p_value = f_oneway(class1, class2, class3, class4)# Output the results
print("F-statistic:", f_statistic)
print("P-value:", p_value)# Interpret the results
alpha = 0.05
if p_value < alpha:print("There is a significant difference in the effectiveness of the teaching methods.")
else:print("There is no significant difference in the effectiveness of the teaching methods.")
F-statistic: 22.045992451864645
P-value: 1.5622062333927252e-07
There is a significant difference in the effectiveness of the teaching methods.2.计算SS、df和F值
import numpy as np
import pandas as pd
from scipy.stats import f_oneway, f# Data for the four classes
class1 = [75, 77, 70, 88, 72, 80, 79, 81]
class2 = [93, 80, 85, 90, 84, 86, 85, 81]
class3 = [65, 67, 77, 68, 65, 64, 62, 68]
class4 = [72, 70, 71, 65, 81, 72, 68, 74]# Perform one-way ANOVA
f_statistic, p_value = f_oneway(class1, class2, class3, class4)# Degrees of freedom
num_groups = 4
num_samples = len(class1) + len(class2) + len(class3) + len(class4)
df_between = num_groups - 1
df_within = num_samples - num_groups# Calculate sum of squares (SS)
mean_total = np.mean([np.mean(class1), np.mean(class2), np.mean(class3), np.mean(class4)])
ss_total = np.sum((np.concatenate([class1, class2, class3, class4]) - mean_total) ** 2)
ss_between = np.sum([len(class1) * (np.mean(class1) - mean_total) ** 2,len(class2) * (np.mean(class2) - mean_total) ** 2,len(class3) * (np.mean(class3) - mean_total) ** 2,len(class4) * (np.mean(class4) - mean_total) ** 2])
ss_within = np.sum((class1 - np.mean(class1)) ** 2) + \np.sum((class2 - np.mean(class2)) ** 2) + \np.sum((class3 - np.mean(class3)) ** 2) + \np.sum((class4 - np.mean(class4)) ** 2)# Calculate mean squares (MS)
ms_between = ss_between / df_between
ms_within = ss_within / df_within# Calculate F-statistic
f_statistic_manual = ms_between / ms_within# Critical F-value
alpha = 0.05
f_crit = f.ppf(1 - alpha, df_between, df_within)# Create a DataFrame for better tabular representation
data = {'Class 1': class1,'Class 2': class2,'Class 3': class3,'Class 4': class4,
}df = pd.DataFrame(data)# Output the ANOVA results
print("Analysis of Variance (ANOVA):")
print("F-statistic (from scipy.stats):", f_statistic)
print("P-value (from scipy.stats):", p_value)
print("\nManual Calculation:")
print("SS Between:", ss_between)
print("SS Within:", ss_within)
print("DF Between:", df_between)
print("DF Within:", df_within)
print("MS Between:", ms_between)
print("MS Within:", ms_within)
print("F-statistic (manual calculation):", f_statistic_manual)
print("Critical F-value:", f_crit)# Interpret the results
if p_value < alpha:print("\nThere is a significant difference in the effectiveness of the teaching methods.")
else:print("\nThere is no significant difference in the effectiveness of the teaching methods.")
Manual Calculation:
SS Between: 1538.59375
SS Within: 651.375
DF Between: 3
DF Within: 28
MS Between: 512.8645833333334
MS Within: 23.263392857142858
F-statistic (manual calculation): 22.045992451864645
Critical F-value: 2.9466852660172655相关文章:

scipy实现单因素方差分析
经典例题 某校高二年级共有四个班,采用四种不同的教学方法进行数学教学,为了比较这四种教学法的效果是否存在明显的差异,期末统考后,从这四个班中各抽取 5 名考生的成绩,如下所示。 班级 一班 二班 三班 四班 …...
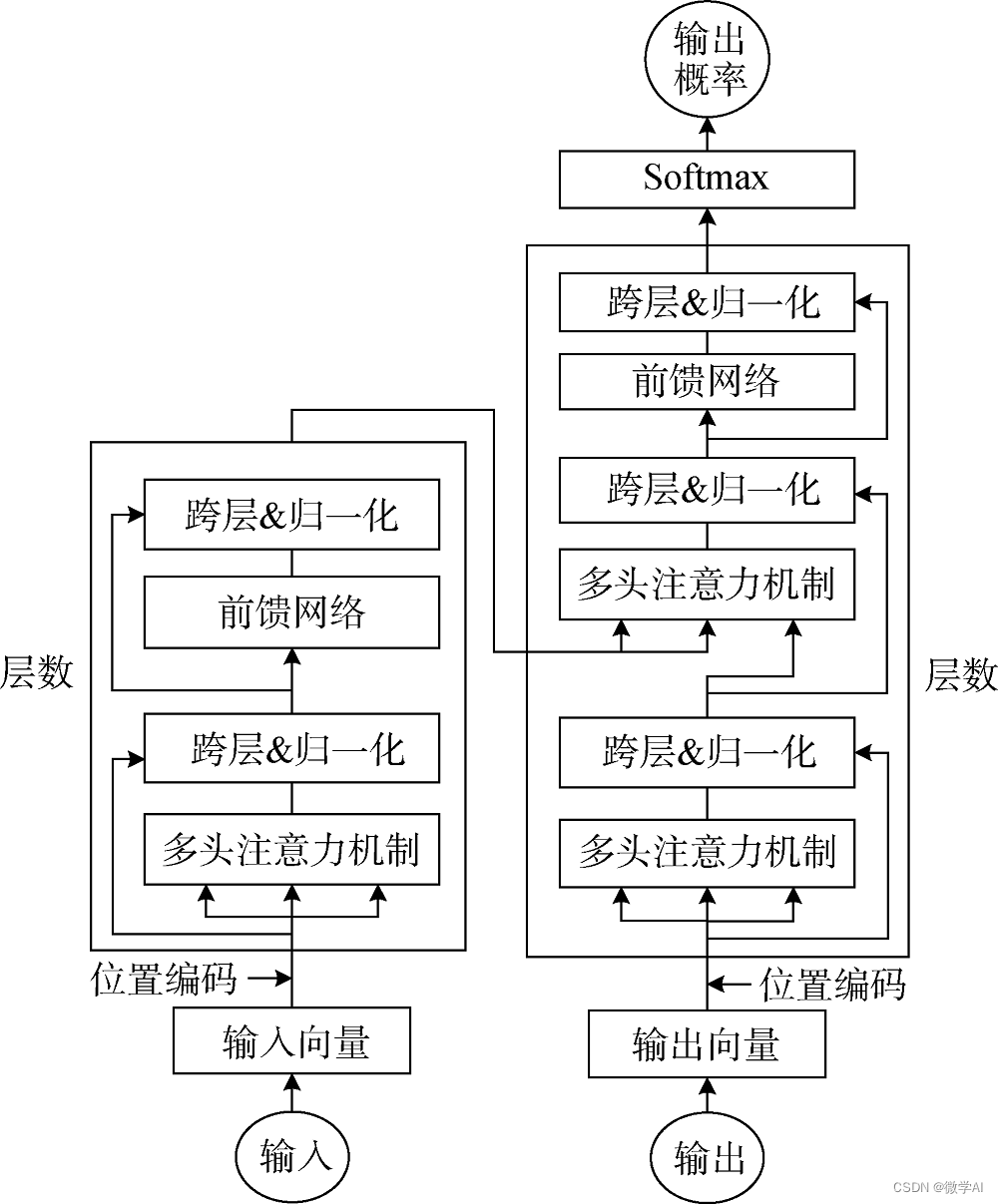
深度学习实战59-NLP最核心的模型:transformer的搭建与训练过程详解,手把手搭建与跑通
大家好,我是微学AI,今天给大家介绍一下深度学习实战59-NLP最核心的模型:transformer的搭建与训练过程详解,手把手搭建与跑通。transformer是一种基于自注意力机制的深度学习模型,由Vaswani等人在2017年的论文《Attention is All You Need》中提出。它最初被设计用来处理序…...
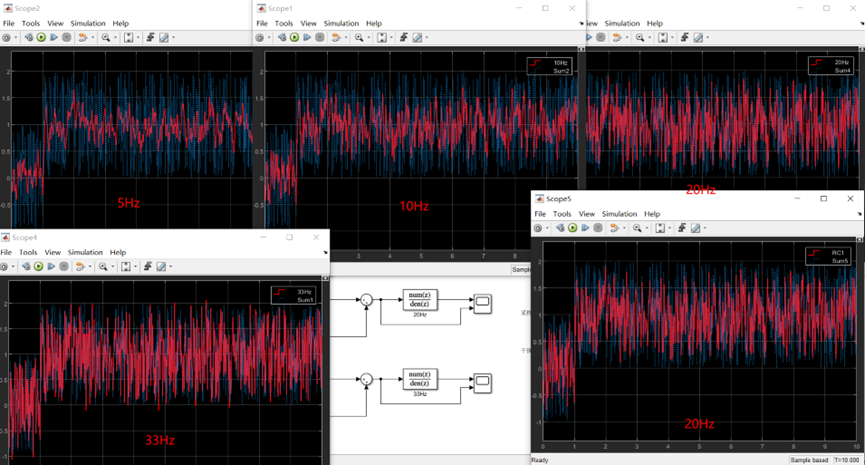
一阶滤波器(一阶巴特沃斯滤波器)
连续传递函数G(s) 离散传递函数G(z) 转换为差分方程形式 一阶巴特沃斯滤波器Filter Designer参数设计:参考之前的博客Matlab的Filter Designer工具设计二阶低通滤波器 设计采样频率100Hz,截止频率20Hz。 注意:设计参数使用在离散系统中&…...
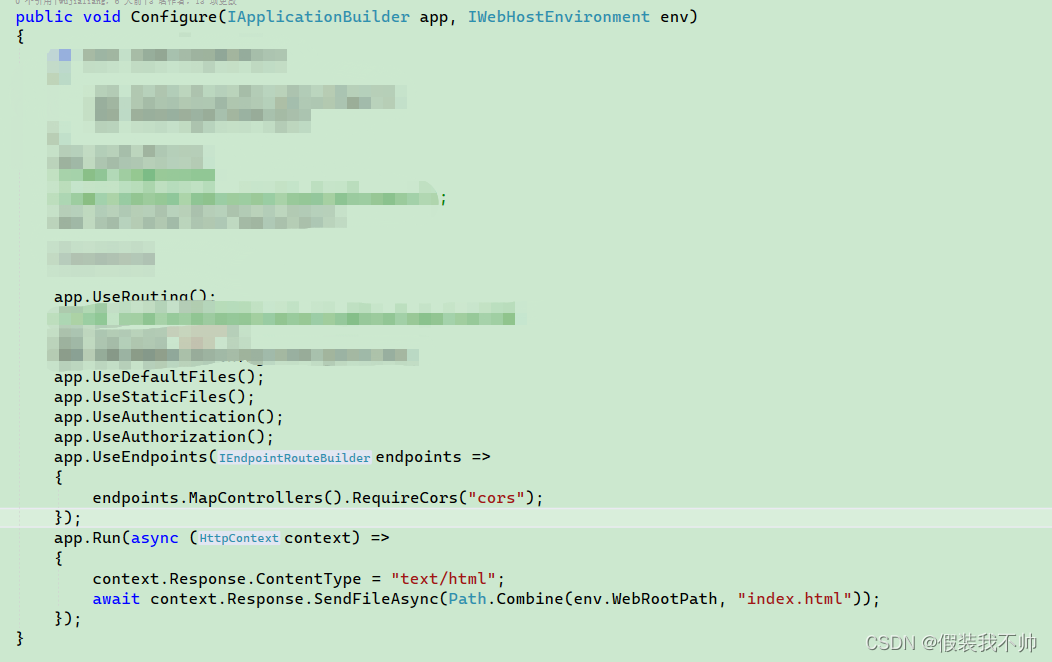
.net core中前端vue HTML5 History 刷新页面404问题
放到启动的应用程序的最后面 app.Run(async (context) > {context.Response.ContentType "text/html";await context.Response.SendFileAsync(Path.Combine(env.WebRootPath, "index.html")); });https://blog.csdn.net/lee576/article/details/88355…...
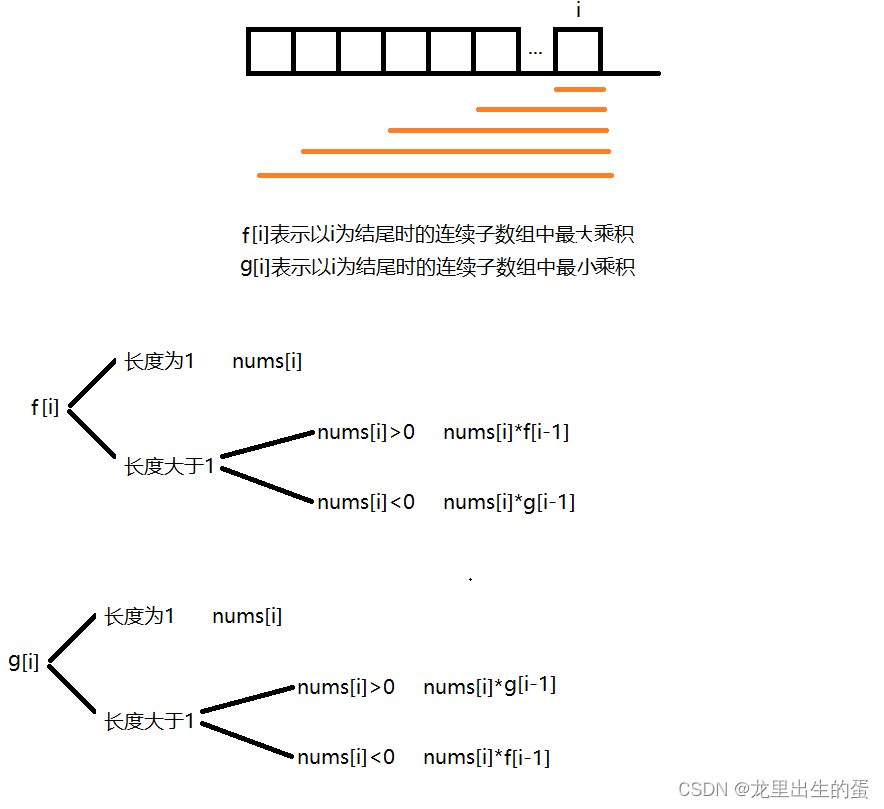
【152.乘积最大子数组】
目录 一、题目描述二、算法原理三、代码实现 一、题目描述 二、算法原理 三、代码实现 class Solution { public:int maxProduct(vector<int>& nums) {int nnums.size();vector<int> f(n);vector<int> g(n);f[0]g[0]nums[0];int retnums[0];for(int i1;…...

如何开发OA系统场景的系统架构
1.开发OA系统场景的系统架构 针对开发OA系统的场景,以下是一个简单的系统架构示例,包括前端、后端和数据库三个基本部分: 前端: 使用React框架进行前端开发,构建用户界面和交互逻辑。前端模块包括日程管理模块、文档管…...

spring boot 集成 RedisSearch 和 RedisJSON
1. 准备工作 环境说明 java 8;redis7.2.2,redis集成RedisSearch、redisJson 模块;spring boot 2.5在执行 redis 命令, 或者监控 程序执行的redis 指令时,可以采用 redisinsight查看,下载地址。 背景说明 需…...

【Kotlin精简】第8章 协程
1 简介 Kotlin 中的协程提供了一种全新处理并发的方式,您可以在 Android 平台上使用它来简化异步执行的代码。协程是从 Kotlin 1.3 版本开始引入,但这一概念在编程世界诞生的黎明之际就有了,最早使用协程的编程语言可以追溯到 1967 年的 Sim…...
【MATLAB源码-第79期】基于蚯蚓优化算法(EOA)的栅格路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 蚯蚓优化算法(Earthworm Optimisation Algorithm, EOA)是一种启发式算法,灵感来源于蚯蚓在自然界中的行为模式。蚯蚓优化算法主要模仿了蚯蚓在寻找食物和逃避天敌时的行为策略。以下是蚯蚓…...

RPC实现简单解析
RPC是什么,先摘取一段解释: RPC全称为远程过程调用(Remote Procedure Call),它是一种计算机通信协议,允许一个计算机程序调用另一个计算机上的子程序,而无需了解底层网络细节。通过RPCÿ…...

【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr
【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr 文章目录 【Ubuntu】Ubuntu20.04下安装视频播放器vlc和录屏软件ssr1. 安装视频播放器vlc2. 安装录屏软件ssr 1. 安装视频播放器vlc sudo apt-get install vlcvlc是一款比较简洁的视频播放器,如下所示 2. 安…...
WMS仓储管理系统与TMS系统整合后的优势
随着全球化的加速和供应链网络的日益复杂,仓库和运输成为企业运营中的两个关键环节。为了更高效地管理这两个环节,许多企业开始探索将WMS仓储管理系统和TMS运输管理系统整合的可能性。这种整合不仅可以提升仓库流程的可见性,还有助于改善调度…...

测试的专用
测试...
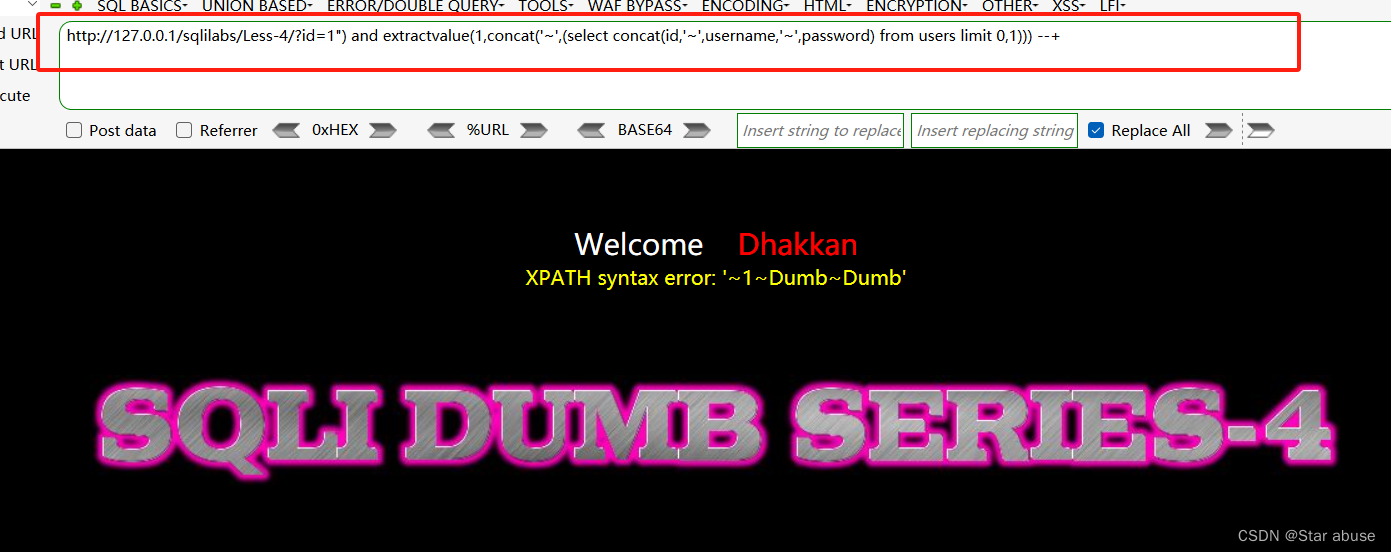
sqli-labs(Less-4) extractvalue闯关
extractvalue() - Xpath类型函数 1. 确认注入点如何闭合的方式 2. 爆出当前数据库的库名 http://127.0.0.1/sqlilabs/Less-4/?id1") and extractvalue(1,concat(~,(select database()))) --3. 爆出当前数据库的表名 http://127.0.0.1/sqlilabs/Less-4/?id1") …...
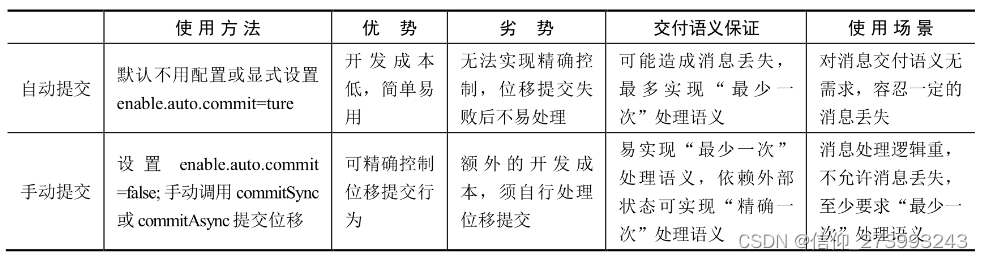
Kafka简单汇总
Kafka的结构图 多个Parttion共同组成这个topic的所有消息。每个consumer都属于一个consumer group,每条消息只能被consumer group中的一个Consumer消费, 但可以被多个consumer group消费。即组间数据是共享的,组内数据是竞争的。二、消费模型…...

任务交给谁?委派模式告诉你最佳选择!
文章目录 一、概念二、角色三、代码实现四、委派模式在源码中的体现五、委派模式的优缺点优点缺点 一、概念 委派模式(Delegate Pattern)又叫委托模式,是一种面向对象的设计模式。委派模式是一种行为模式,不属于GOF23种设计模式之中基本作用…...

【JavaEE】Servlet(创建Maven、引入依赖、创建目录、编写及打包、部署和验证、smart Tomcat)
一、什么是Servlet? Servlet 是一种实现动态页面的技术. 是一组 Tomcat 提供给程序猿的 API, 帮助程序猿简单高效的开发一个 web app 1.1 Servlet能干什么? 🚕允许程序猿注册一个类, 在 Tomcat 收到某个特定的 HTTP 请求的时候, 执行这个类…...
降低城市内涝风险,万宾科技内涝积水监测仪的作用
频繁的内涝会削弱和损坏城市的关键基础设施,包括道路、桥梁和公用设施。城市内涝风险降低可以减少交通中断事件,也可以保护居民安全并降低路面维修等成本,进一步确保城市基本服务继续发挥作用。对城市可持续发展来讲有效减少内涝的风险是重要…...

水库大坝安全监测预警系统的重要作用
水库大坝建造在地质构造复杂、岩土特性不均匀的地基上,在各种荷载的作用和自然因素的影响下,其工作性态和安全状况随时都在变化。如果出现异常,又不被及时发现,其后果不堪设想。全天候实时监测,实时掌握水库水位、雨情…...

【AI视野·今日NLP 自然语言处理论文速览 第六十五期】Mon, 30 Oct 2023
AI视野今日CS.NLP 自然语言处理论文速览 Mon, 30 Oct 2023 Totally 67 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers An Approach to Automatically generating Riddles aiding Concept Attainment Authors Niharika Sri Parasa,…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
