2736. 最大和查询 : 从一维限制到二维限制,逐步思考剖析本题(进阶一问)
题目描述
这是 LeetCode 上的 「2736. 最大和查询」 ,难度为 「困难」。
Tag : 「排序」、「离散化」、「树状数组」
给你两个长度为 n、下标从 0 开始的整数数组 nums1 和 nums2,另给你一个下标从 1 开始的二维数组 queries,其中 。
对于第 i 个查询,在所有满足 且 的下标 j ( ) 中,找出 的 最大值 ,如果不存在满足条件的 j 则返回 。
返回数组 answer,其中 answer[i] 是第 i 个查询的答案。
示例 1:
输入:nums1 = [4,3,1,2], nums2 = [2,4,9,5], queries = [[4,1],[1,3],[2,5]]
输出:[6,10,7]
解释:
对于第 1 个查询:xi = 4 且 yi = 1 ,可以选择下标 j = 0 ,此时 nums1[j] >= 4 且 nums2[j] >= 1 。nums1[j] + nums2[j] 等于 6 ,可以证明 6 是可以获得的最大值。
对于第 2 个查询:xi = 1 且 yi = 3 ,可以选择下标 j = 2 ,此时 nums1[j] >= 1 且 nums2[j] >= 3 。nums1[j] + nums2[j] 等于 10 ,可以证明 10 是可以获得的最大值。
对于第 3 个查询:xi = 2 且 yi = 5 ,可以选择下标 j = 3 ,此时 nums1[j] >= 2 且 nums2[j] >= 5 。nums1[j] + nums2[j] 等于 7 ,可以证明 7 是可以获得的最大值。
因此,我们返回 [6,10,7] 。
示例 2:
输入:nums1 = [3,2,5], nums2 = [2,3,4], queries = [[4,4],[3,2],[1,1]]
输出:[9,9,9]
解释:对于这个示例,我们可以选择下标 j = 2 ,该下标可以满足每个查询的限制。
示例 3:
输入:nums1 = [2,1], nums2 = [2,3], queries = [[3,3]]
输出:[-1]
解释:示例中的查询 xi = 3 且 yi = 3 。对于每个下标 j ,都只满足 nums1[j] < xi 或者 nums2[j] < yi 。因此,不存在答案。
提示:
离散化 + 排序 + 树状数组
根据题意,两个等长的数组 num1 和 nums2,只能是相同下标的元素凑成一对。
我们不妨用两个一维数组 nums1 和 nums2 构建出一个二维数组 nums,方便后续处理,其中 。
同时对 queries 进行简单拓展,构建新的二维数组 nq,目的是对原有下标信息进行记录,其中 (此处构建新 nq 的作用,下文会说)。
好了,现在我们有两个新的数组 nums 和 nq,接下来所有讨论都会针对新数组进行。
我希望你牢牢记住:** 是对 nums1 和 nums2 的简单合并;而 是对 queries 原有下标的拓展记录**。
做完简单的预处理工作后,来思考一个前置问题:
假设其他内容不变,要求从满足「 且 」调整为仅需满足「 」,我们会如何求解?
一个简单的做法:
-
对
nums中的第一维(即 )和nq中第一维(即 )排倒序; -
从前往后处理每个询问 ,同时使用变量
idx对nums进行扫描,若满足 时,将idx右移,同时记录已被扫描的数对和 。当
idx不能再后移时,说明当前所有满足 要求的数对已被扫描完,在记录的数对和中取最大值,即是当前询问 的答案 (此处解释了为什么需要构造新数组nq,因为询问处理是按照排序后进行,但在ans中需要映射回原有顺序)。 -
重复步骤 ,直到处理完所有询问。
搞定前置问题后,回到原问题,需要满足「 且 」要求。
进一步思考,排序 + 调整询问顺序,只能解决其中一维限制要求,另一维该如何处理?
或者更加直接的问题:如何在被记录的所有数对和 中找出那些满足 的最大数对和。
不失一般性,假设当前处理到的是 ,其中 的限制要求,通过前置问题的排序方式解决了。另外的 「 我们希望作为“位置信息”,数对和 作为“值信息”进行记录」。
由于条件 ,我们需要对将要作为“位置信息”添加到树状数组的 和 进行离散化,将其映射到 范围内。
对于每个询问,都需要找到已遍历过的大于 的位置上的最大值,把离散化后的值域换成数组坐标,相当于求后缀最大值,后缀最大值可通过相反数,变成求前缀最大值。
能够实现类似的前缀操作,支持“单点修改”和“区间查询”的数据结构是「树状数组」。
Java 代码:
class Solution {
int sz;
int[] tr;
int lowbit(int x) {
return x & -x;
}
void add(int a, int b) {
for (int i = a; i <= sz; i += lowbit(i)) tr[i] = Math.max(tr[i], b);
}
int query(int x) {
int ans = -1;
for (int i = x; i > 0; i -= lowbit(i)) ans = Math.max(ans, tr[i]);
return ans;
}
public int[] maximumSumQueries(int[] nums1, int[] nums2, int[][] queries) {
int n = nums1.length, m = queries.length;
// 构建新的 nums 和 nq
int[][] nums = new int[n][2];
for (int i = 0; i < n; i++) nums[i] = new int[]{nums1[i], nums2[i]};
int[][] nq = new int[m][3];
for (int i = 0; i < m; i++) nq[i] = new int[]{queries[i][0], queries[i][1], i};
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
Set<Integer> set = new HashSet<>();
for (int[] x : nums) set.add(x[1]);
for (int[] q : nq) set.add(q[1]);
List<Integer> list = new ArrayList<>(set);
Collections.sort(list);
sz = list.size();
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < sz; i++) map.put(list.get(i), i);
// 调整询问顺序, 解决其中一维限制
Arrays.sort(nums, (a,b)->b[0]-a[0]);
Arrays.sort(nq, (a,b)->b[0]-a[0]);
tr = new int[sz + 10];
Arrays.fill(tr, -1);
int[] ans = new int[m];
int idx = 0;
for (int[] q : nq) {
int x = q[0], y = q[1], i = q[2];
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - map.get(nums[idx][1]), nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - map.get(y)); // 查询树状数组中的最值
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int sz;
vector<int> tr;
int lowbit(int x) {
return x & -x;
}
void add(int a, int b) {
for (int i = a; i <= sz; i += lowbit(i)) tr[i] = max(tr[i], b);
}
int query(int x) {
int ans = -1;
for (int i = x; i > 0; i -= lowbit(i)) ans = max(ans, tr[i]);
return ans;
}
vector<int> maximumSumQueries(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& queries) {
int n = nums1.size(), m = queries.size();
// 构建新的 nums 和 nq
vector<vector<int>> nums(n, vector<int>(2));
vector<vector<int>> nq(m, vector<int>(3));
for (int i = 0; i < n; i++) {
nums[i][0] = nums1[i]; nums[i][1] = nums2[i];
}
for (int i = 0; i < m; i++) {
nq[i][0] = queries[i][0]; nq[i][1] = queries[i][1]; nq[i][2] = i;
}
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
unordered_set<int> set;
for (auto& x : nums) set.insert(x[1]);
for (auto& q : nq) set.insert(q[1]);
vector<int> list(set.begin(), set.end());
sort(list.begin(), list.end());
sz = list.size();
map<int, int> map;
for (int i = 0; i < sz; i++) map[list[i]] = i;
// 调整询问顺序, 解决其中一维限制
sort(nums.begin(), nums.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] > b[0];
});
sort(nq.begin(), nq.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] > b[0];
});
tr.resize(sz + 10, -1);
vector<int> ans(m);
int idx = 0;
for (auto& q : nq) {
int x = q[0], y = q[1], i = q[2];
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - map[nums[idx][1]], nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - map[y]); // 查询树状数组中的最值
}
return ans;
}
};
Python 代码:
class Solution:
def maximumSumQueries(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
sz = 0
tr = []
def lowbit(x):
return x & -x
def add(a, b):
i = a
while i <= sz:
tr[i] = max(tr[i], b)
i += lowbit(i)
def query(x):
ans, i = -1, x
while i > 0:
ans = max(ans, tr[i])
i -= lowbit(i)
return ans
n, m = len(nums1), len(queries)
# 构建新的 nums 和 nq
nums = [(nums1[i], nums2[i]) for i in range(n)]
nq = [(queries[i][0], queries[i][1], i) for i in range(m)]
# 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
unique_set = set()
for x in nums:
unique_set.add(x[1])
for q in nq:
unique_set.add(q[1])
unique_list = list(unique_set)
unique_list.sort()
sz = len(unique_list)
mapping = {val: idx for idx, val in enumerate(unique_list)}
# 调整询问顺序, 解决其中一维限制
nums.sort(key=lambda x: x[0], reverse=True)
nq.sort(key=lambda x: x[0], reverse=True)
tr = [-1] * (sz + 10)
ans = [0] * m
idx = 0
for x, y, i in nq:
# 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while idx < n and nums[idx][0] >= x:
add(sz - mapping[nums[idx][1]], nums[idx][0] + nums[idx][1])
idx += 1
ans[i] = query(sz - mapping[y]) # 查询树状数组中的最值
return ans
TypeScript 代码:
function maximumSumQueries(nums1: number[], nums2: number[], queries: number[][]): number[] {
let sz = 0;
let tr = [];
const lowbit = function(x: number): number {
return x & -x;
}
const add = function(a: number, b: number): void {
for (let i = a; i <= sz; i += lowbit(i)) tr[i] = Math.max(tr[i], b);
}
const query = function(x: number): number {
let ans = -1;
for (let i = x; i > 0; i -= lowbit(i)) ans = Math.max(ans, tr[i]);
return ans;
}
const n = nums1.length, m = queries.length;
// 构建新的 nums 和 nq
const nums = Array.from({ length: n }, (_, i) => [nums1[i], nums2[i]]);
const nq = Array.from({ length: m }, (_, i) => [...queries[i], i]);
// 对要添加到树状数组的 nums[i][1] 和 nq[i][1] 进行离散化(构建映射字典, 将原值映射到 [0, m - 1])
const set: Set<number> = new Set();
for (const x of nums) set.add(x[1]);
for (const q of nq) set.add(q[1]);
const list: number[] = [...set];
list.sort((a, b) => a - b);
sz = list.length;
const mapping = new Map();
for (let i = 0; i < sz; i++) mapping.set(list[i], i);
// 调整询问顺序, 解决其中一维限制
nums.sort((a, b) => b[0] - a[0]);
nq.sort((a, b) => b[0] - a[0]);
tr = Array(sz + 10).fill(-1);
const ans = Array(m).fill(0);
let idx = 0;
for (let [x, y, i] of nq) {
// 扫描所有满足 nums[idx][0] >= x 的数对, 添加到树状数组中(其中离散值作为位置信息, 数对和作为值信息)
while (idx < n && nums[idx][0] >= x) {
add(sz - mapping.get(nums[idx][1])!, nums[idx][0] + nums[idx][1]);
idx++;
}
ans[i] = query(sz - mapping.get(y)!); // 查询树状数组中的最值
}
return ans;
};
-
时间复杂度:令 nums1长度为 ,queries长度为 ,构建nums和nq的复杂度为 ;离散化复杂度为 ;对nums和nq的排序复杂度为 ;构建答案复杂度为 。整体复杂度为 -
空间复杂度:
进阶
本题解讲述了「从一维到二维偏序问题」时,可通过「一维排序,一维树状数组」求通解。
那三维偏序问题呢?是否存在通用的解决思路。
答:一维排序,一维归并,一维树状数组。
最后
这是我们「刷穿 LeetCode」系列文章的第 No.2736 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:
)
2736. 最大和查询 : 从一维限制到二维限制,逐步思考剖析本题(进阶一问)
题目描述 这是 LeetCode 上的 「2736. 最大和查询」 ,难度为 「困难」。 Tag : 「排序」、「离散化」、「树状数组」 给你两个长度为 n、下标从 0 开始的整数数组 nums1 和 nums2,另给你一个下标从 1 开始的二维数组 queries,其中 。 对于第…...

2023数维杯国际数学建模A题B题C题D题思路+模型+代码+完整论文
目录 1.数维杯各题思路模型:比赛开始后,第一时间更新,获取见文末名片 3 常见数模问题常见模型分类 3.1 分类问题 3.2 优化问题 详细思路见此名片,开赛第一时间更新 1.数维杯各题思路模型:9.7晚上比赛开始后&#x…...

java多个jar包编译生成.class文件
有时候需要通过多个jar包让java文件生成 .class字节码文件,这里主要记录一下格式问题 javac -cp a.jar;b.jar a.java...

小米手环8pro重新和手机配对解决办法
如果更换了手机,那么小米手环8pro是无法和新手机自动连接的。 但是在新手机上直接连接又连接不上,搜索蓝牙根本找不到手环的蓝牙。 解决办法就是: 把手环恢复出厂!!!!! 是的&…...
element-china-area-data插件vue3做省市区的下拉选择,用3个独立的el-select实现
第1版,选择下拉没有优化 第2版,选择下拉时,做了优化...

盘点十大免费低/无代码开发软件,数字化转型看这里
在数字化日益普及的当下,低代码开发技术逐渐受到大众的追捧。这种技术让缺乏编程经验的大众也能轻松创建应用程序和网站。通过直观的图形界面和拖拽功能,用户可以无需编写任何代码,轻松实现自己的开发需求。本文将为您介绍十大免费的低代码开…...
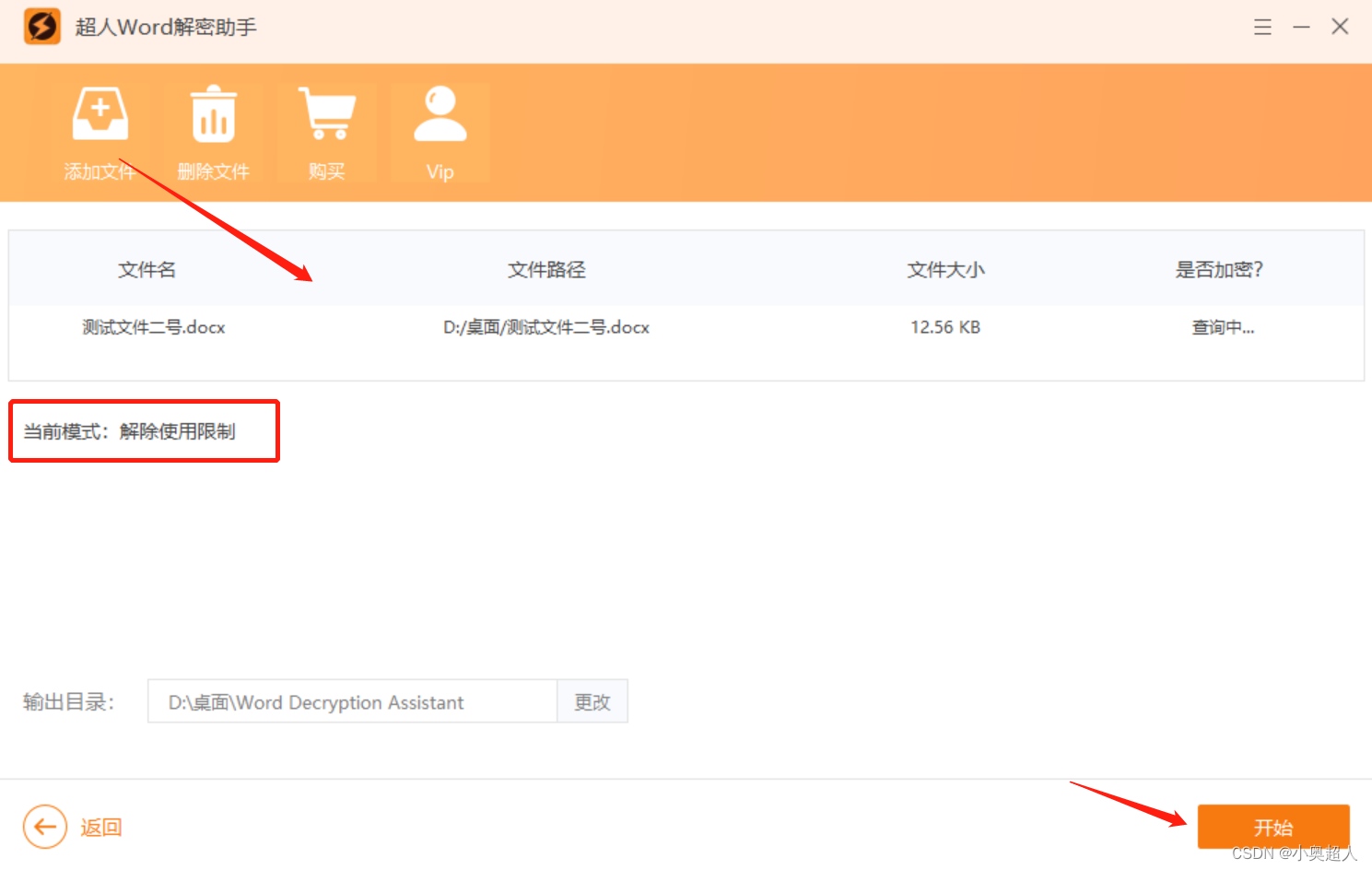
【word密码】word设置只读方式的四个方法
想要将word文档设置为只读模式,方法有很多,今天小奥超人介绍几个方法给大家。 方法一:文件属性 常见的、简单的设置方法,不用打开word文件,只需要右键选择文件,打开文件属性,勾选上【只读】选…...

正整数的阶乘
阶乘是基斯顿卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。 一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶…...
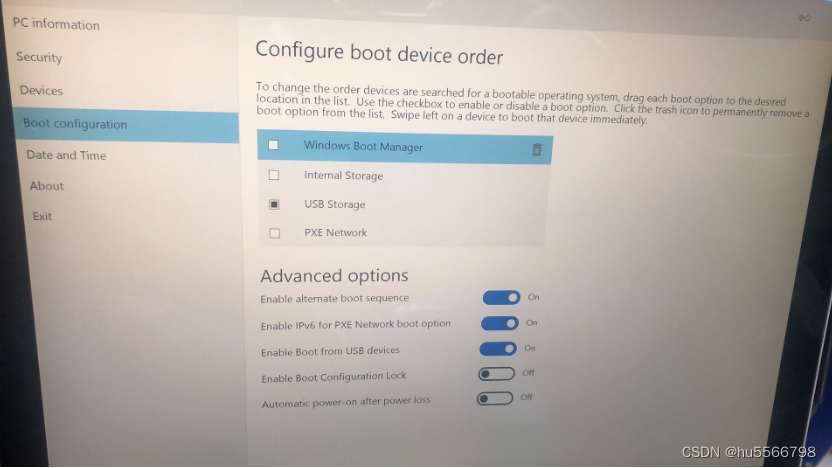
微软Surface/Surface pro笔记本电脑进入bios界面
微软Surface笔记本电脑进入bios界面 方法一推薦這種方法:Surface laptop 进BIOS步骤 开机后,不停按音量键进bios界面。 方法二:Surface Book、Surface Pro进bios步骤 1、关闭Surface,然后等待大约10秒钟以确保其处于关闭状态。…...

暂存2暂存2暂存2
暂存2暂存2暂存2...
深入理解TensorFlow:计算图的重要性与应用
TensorFlow是一个流行而强大的机器学习框架,其核心概念之一是计算图(computation graph)。计算图在TensorFlow中扮演着重要角色,作为一种数据流图表示形式,它能够将计算的过程可视化,同时方便优化、分布式计…...

20231114在HP笔记本的ubuntu20.04系统下向RealmeQ手机发送PDF文件
20231114在HP笔记本的ubuntu20.04系统下向RealmeQ手机发送PDF文件 2023/11/14 14:11 手机:Realme Q 笔记本电脑:HP https://item.jd.com/100012583174.html 惠普(HP)战66 三代AMD版 14英寸轻薄笔记本电脑(锐龙7nm 六核…...

【0234】PgBackendStatus 记录当前postgres进程的活动状态
1. 关于PgBackendStatus 每个存活的后端进场在共享内存中维护一个PgBackendStatus结构体,显示其当前活动状态。(结构体是根据BackendId分配的,但这并不重要。) 请注意: 进场状态收集器进程不参与、甚至不访问这些结构。 每个辅助进程还在共享内存中维护一个PgBackendStatu…...

存钱虚拟计划,嘚
存钱计划—虚拟 2024年 (第一年) 1月 2月 3月 4月 5月 6 月 7月 8月 9月 10月 11月 12月 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 1w 2025年(第二年) 1w1w*102.5% A 懒得写A代替 A A A A A A A A A A 2026年(第三年) (1w1w*10…...
基于IDEA进行Maven工程构建
Java全能学习面试指南:https://javaxiaobear.cn 1. 构建概念和构建过程 项目构建是指将源代码、依赖库和资源文件等转换成可执行或可部署的应用程序的过程,在这个过程中包括编译源代码、链接依赖库、打包和部署等多个步骤。 项目构建是软件开发过程中…...
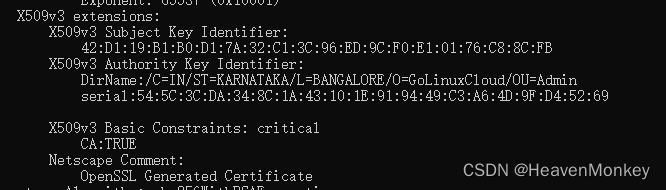
Openssl X509 v3 AuthorityKeyIdentifier实验与逻辑分析
Openssl是X509的事实标准,目前主流OS或个别安全性要求较高的设计场景,对X509的证书链验证已经不在停留在只从数字签名校验了,也就是仅仅从公钥验签的角度,在这些场景中,往往还会校验AuthorityKeyIdentifier和SubjectKe…...

聊聊logback的MDCFilter
序 本文主要研究一下logback的MDCFilter MatchingFilter ch/qos/logback/classic/turbo/MatchingFilter.java public abstract class MatchingFilter extends TurboFilter {protected FilterReply onMatch FilterReply.NEUTRAL;protected FilterReply onMismatch FilterR…...
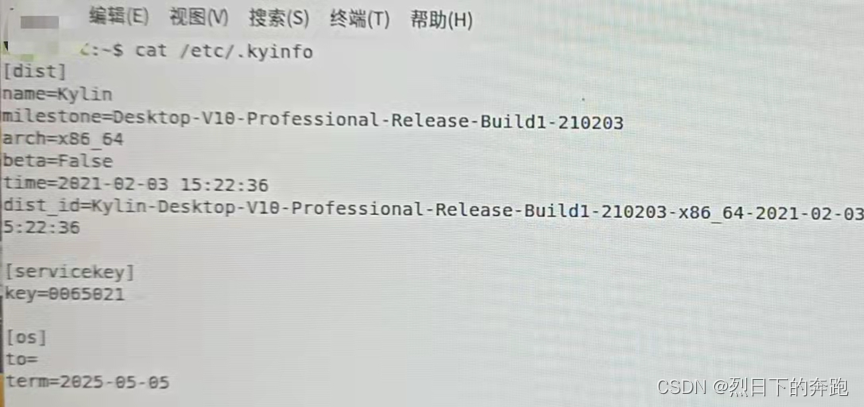
Windows10安装麒麟桌面V10双系统
概述 想要在Windows10操作系统中安装麒麟V10的桌面操作系统(Kylin-Desktop-V10-Professional-Release-Build1-210203-X86_64) 安装前准备 1、先搞清楚自己的电脑类型 A MBR传统bios单硬盘 B MBR 传统bios双硬盘(SSD固态硬盘机械硬盘&…...

file_put_contents锁的问题
记一次线上生产file_put_contents锁的问题 php项目,很多地方加了日志记录,方法为 function logstr($namelog,$str"",$type"Ymd"){$file date("$type")._.$name..log;$add __DIR__./../runtime/cuslog/.date("Ym&q…...
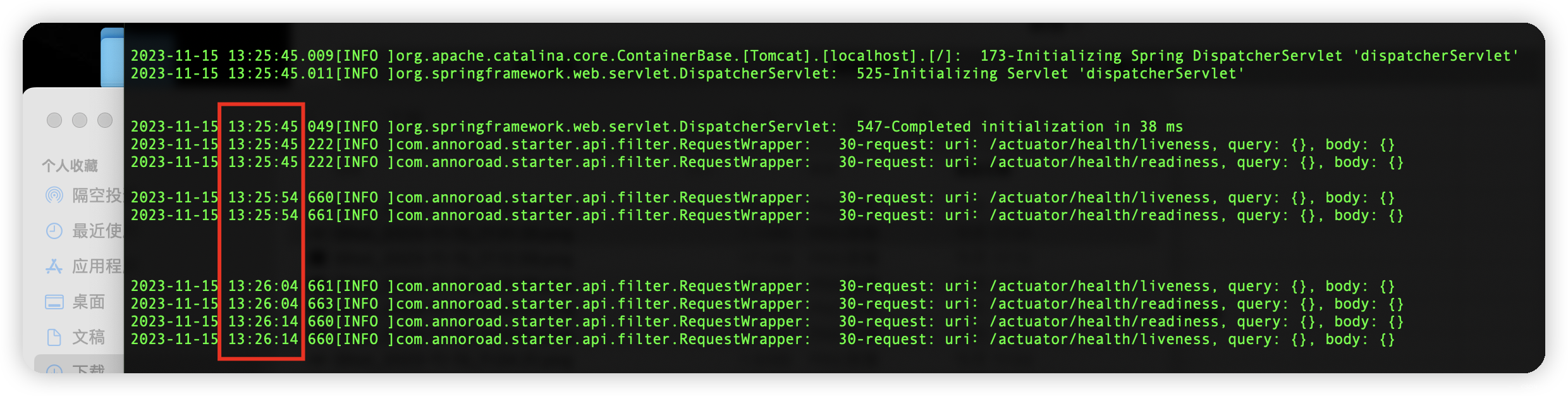
工作中积累的对K8s的就绪和存活探针的一些认识
首先,我的项目是基于 Spring Boot 2.3.5 的,并依赖 spring-boot-starter-actuator 提供的 endpoints 来实现就绪和存活探针,POM 文件如下图: 下面,再让我们来看下与该项目对应的Deployment的YAML文件,如下…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
