2023亚太杯数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录
- 算法介绍
- FP树表示法
- 构建FP树
- 实现代码
- 建模资料
## 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
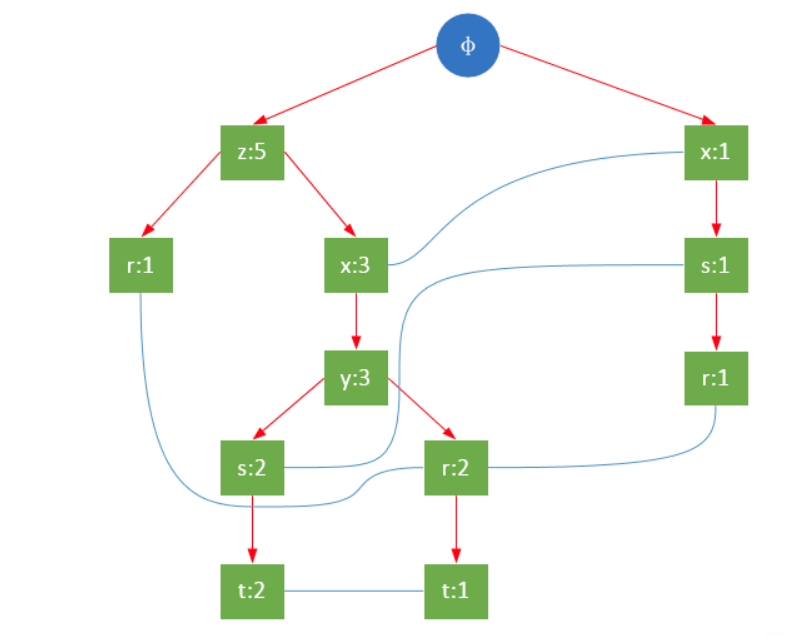
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
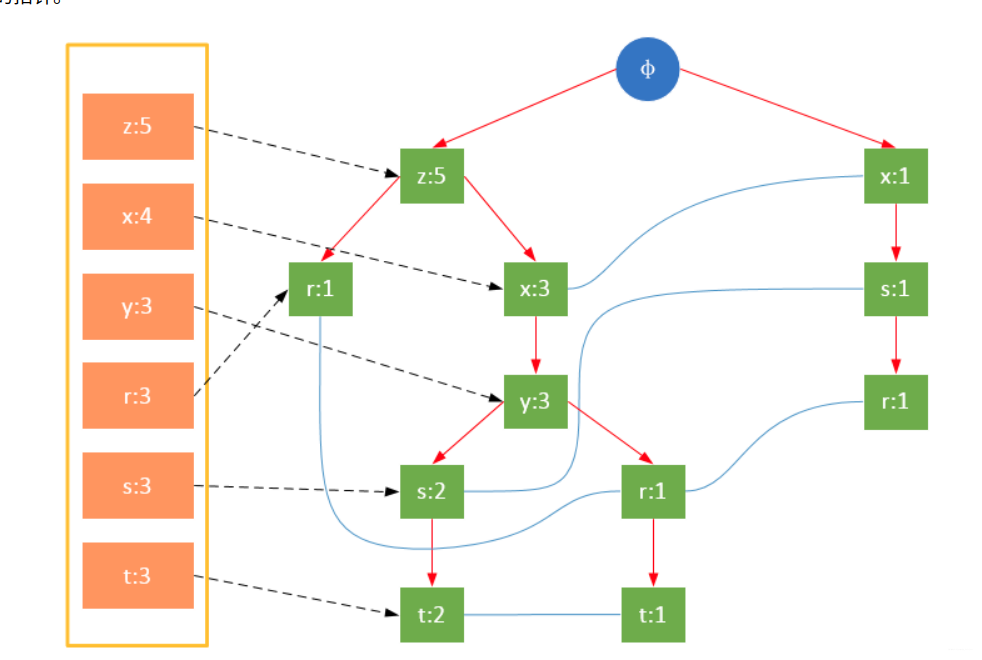
构建FP树
现在有如下数据:
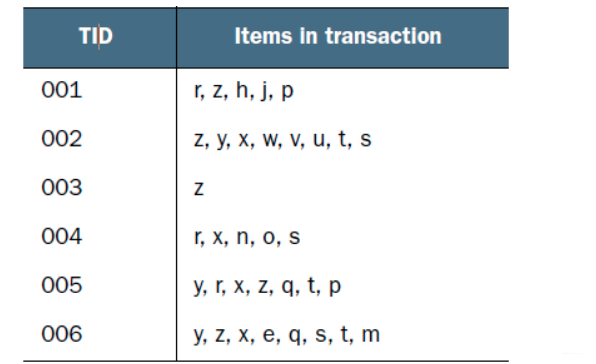
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
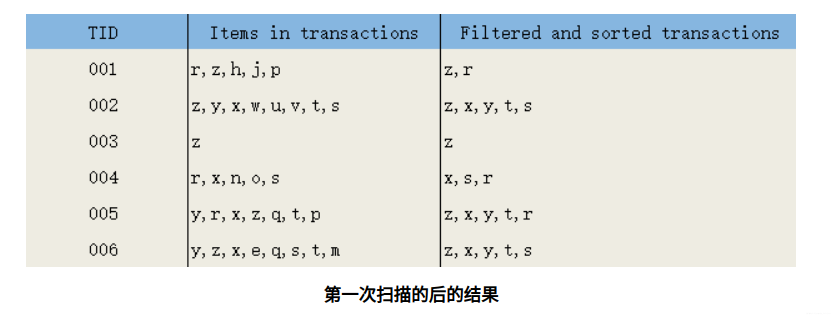
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
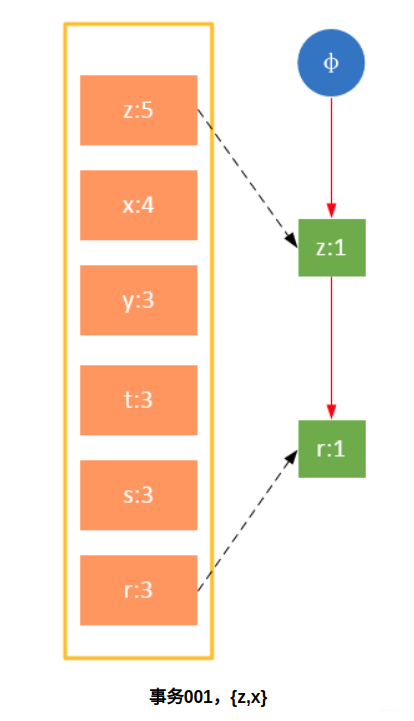
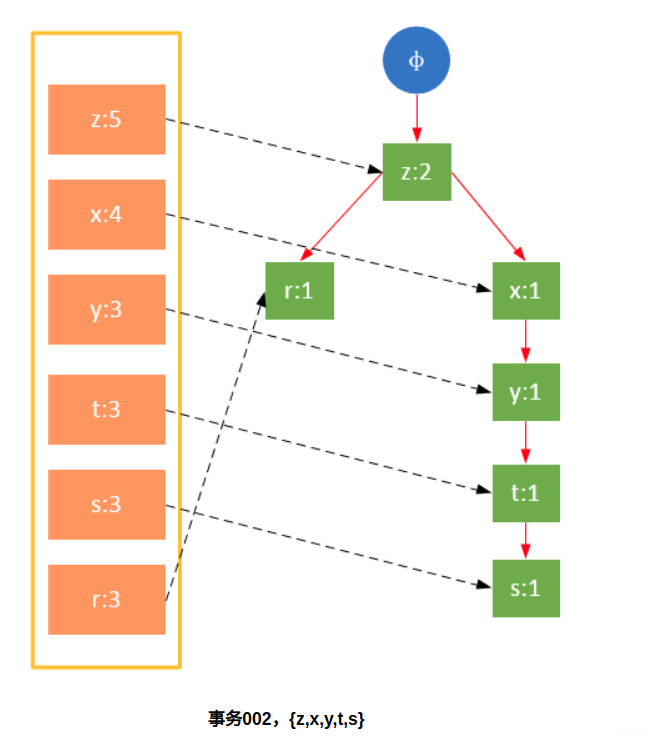
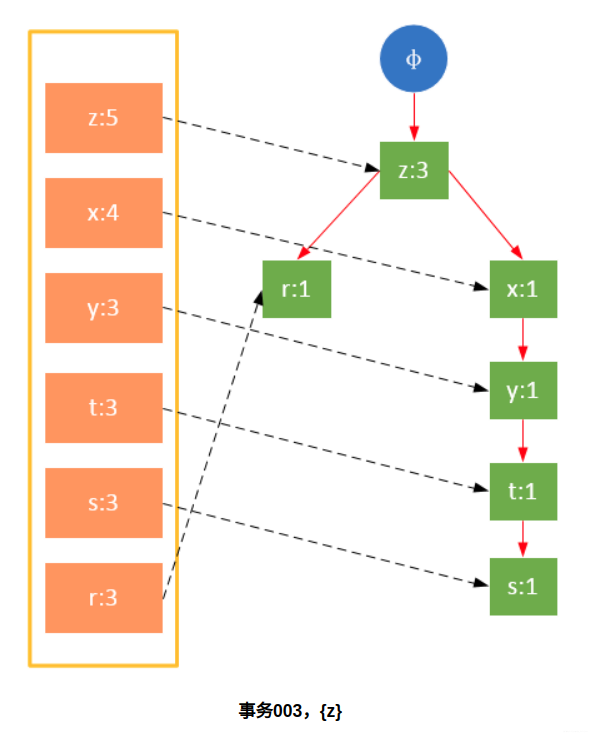
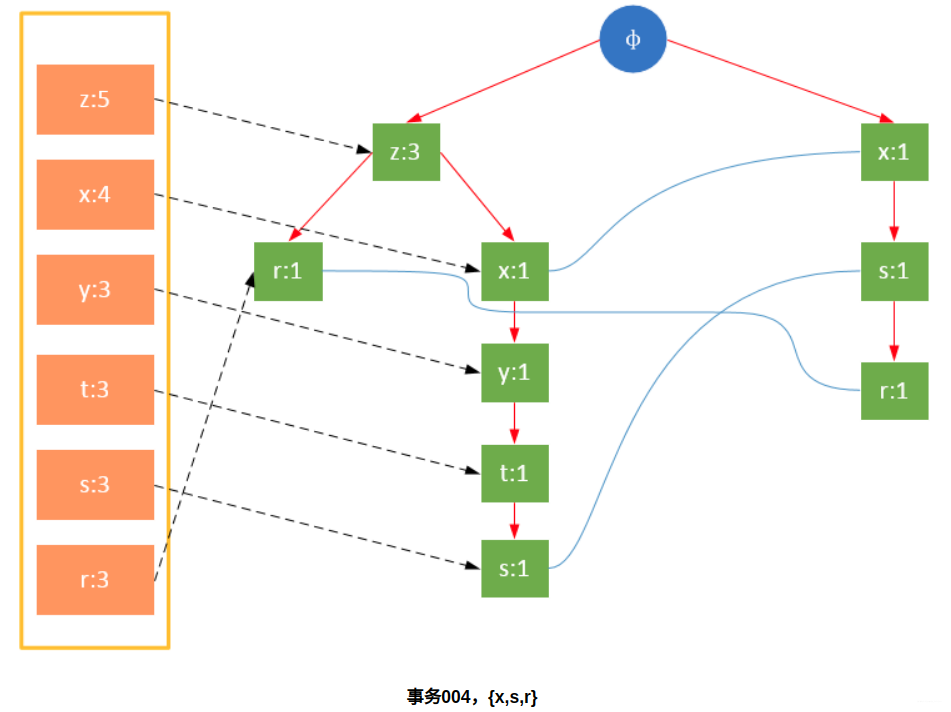
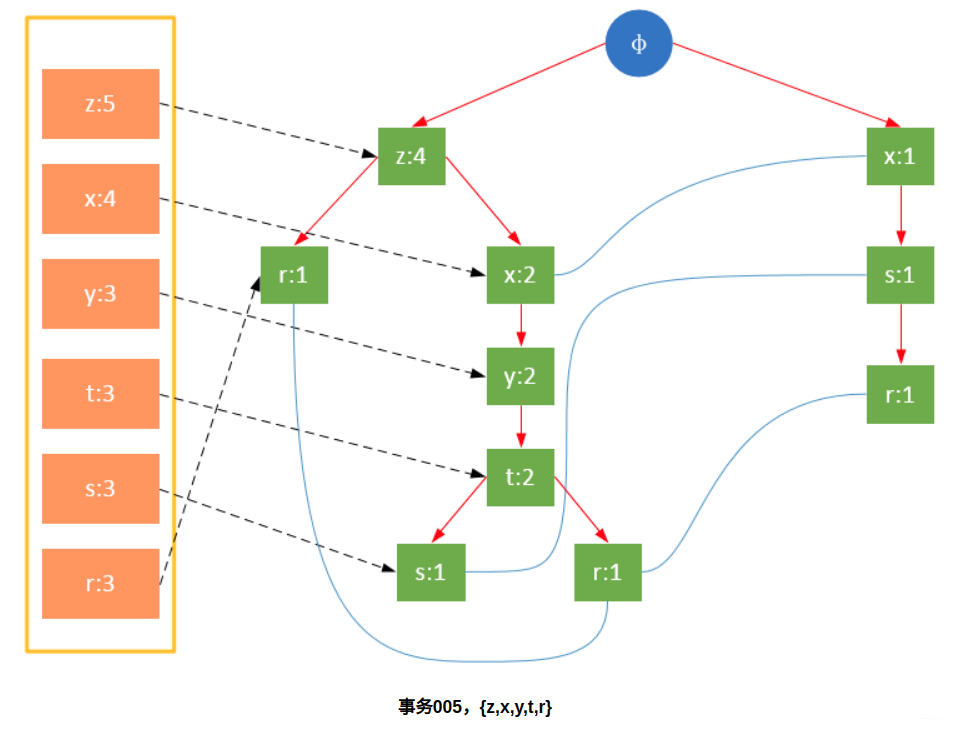
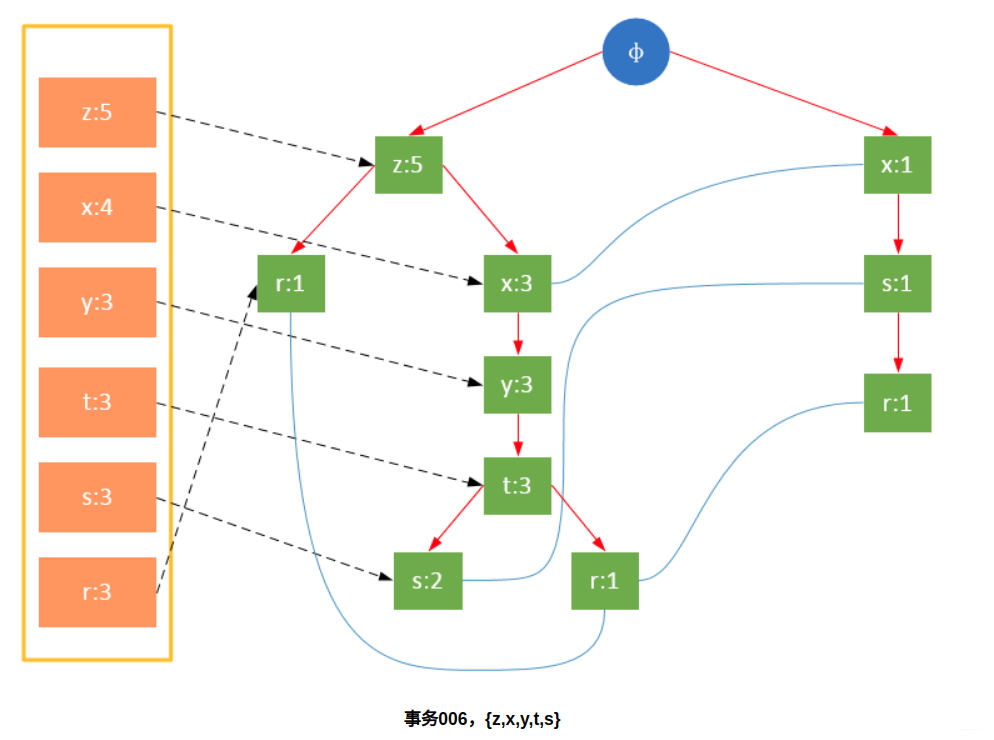
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023亚太杯数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录 算法介绍FP树表示法构建FP树实现代码 建模资料 ## 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,…...

Dart利用私有构造函数_()创建单例模式
文章目录 类的构造函数_()函数dart中构造函数定义 类的构造函数 类的构造函数有两种: 1)默认构造函数: 当实例化对象的时候,会自动调用的函数,构造函数的名称和类的名称相同,在一个类中默认构造函数只能由…...

简述如何使用Androidstudio对文件进行保存和获取文件中的数据
在 Android Studio 中,可以使用以下方法对文件进行保存和获取文件中的数据: 保存文件: 创建一个 File 对象,指定要保存的文件路径和文件名。使用 FileOutputStream 类创建一个文件输出流对象。将需要保存的数据写入文件输出流中…...
面向配电网韧性提升的移动储能预布局与动态调度策略(matlab代码)
欢迎关注威♥“电击小子程高兴的MATLAB小屋”获取更多资料 该程序复现《面向配电网韧性提升的移动储能预布局与动态调度策略》,具体摘要内容见下图,程序主要分为两大模块,第一部分是灾前预防代码,该部分采用两阶段优化算法&#…...
内网信息收集
目录 本机信息收集 查看系统配置信息 查看系统服务信息 查看系统登录信息 自动信息收集 域内信息收集 判断是否存在域 探测域内存主机&端口 powershell arp扫描 小工具 telnet 查看用户&机器&会话相关信息 查看机器相关信息 查看用户相关信息 免费领…...

windows cmd设置代理
https://blog.csdn.net/SHERLOCKSALVATORE/article/details/123599042...
)
English:small classified word(continuously update)
Distant family members(远亲) grandparents (外)祖父母 grandpa grandma grandchildren (外)孙女 aunt 姑姑 / 婶婶 / 姨 / 舅妈 uncle 叔叔 / 姑父 / 姨父/ 舅舅 niece 侄女 / 外甥女 nephew 侄子 / 外甥 cousin 堂 / 表兄弟姐妹 Appearance(外貌) …...
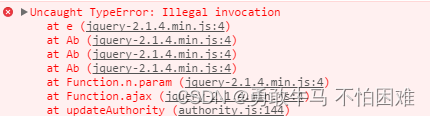
JQuery ajax 提交数据提示:Uncaught TypeError:Illegal invocation
JQuery ajax 提交数据提示:Uncaught TypeError:Illegal invocation 1 问题描述 用jQuery Ajax向DRF接口提交数据的时候,console提示:Uncaught TypeError:Illegal invocation(未捕获的异常:非法调用)。 这个问题可能有两种原因导…...
java实现选择排序
算法步骤 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。重复第二步,直到所有元素均排序完毕。 动图演…...

蓝桥杯 大小写转换
islower/isupper函数 islower和issupper是C标准库中的字符分类函数,用于检查一个字符是否为小写字母或大写字母 需要头文件< cctype>,也可用万能头包含 函数的返回值为bool类型 char ch1A; char ch2b; //使用islower函数判断字符是否为小写字母 if(islower(…...

在誉天学习华为认证,有真机吗
通过培训机构学习华为认证,特别是在HCIE的课程学习中,很多人关心的就是培训机构是否有真机能够进行华为认证的相关实验,今天我们一起来看看,在誉天学习华为认证,有真机吗? 誉天总部数据中心机房和誉天总部一…...
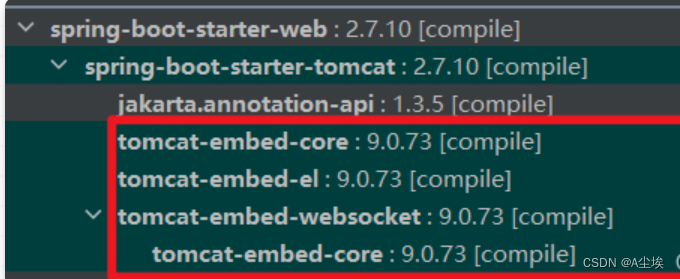
SpringBoot-配置文件properties/yml分析+tomcat最大连接数及最大并发数
SpringBoot配置文件 yaml 中的数据是有序的,properties 中的数据是无序的,在一些需要路径匹配的配置中,顺序就显得尤为重要(例如在 Spring Cloud Zuul 中的配置),此时一般采用 yaml。 Properties ①、位…...

07.智慧商城——商品详情页、加入购物车、拦截器封装token
01. 商品详情 - 静态布局 静态结构 和 样式 <template><div class"prodetail"><van-nav-bar fixed title"商品详情页" left-arrow click-left"$router.go(-1)" /><van-swipe :autoplay"3000" change"onCha…...

查看libc版本
查看libc库版本 查看系统libc版本 $ ldd --version ldd (Ubuntu GLIBC 2.27-3ubuntu1.2) 2.27 Copyright (C) 2018 Free Software Foundation, Inc. This is free software; see the source for copying conditions. There is NO warranty; not even for MERCHANTABILITY or …...

【电路笔记】-快速了解无源器件
快速了解无源器件 文章目录 快速了解无源器件1、概述2、电阻器作为无源器件3、电感器作为无源器件4、电容器作为无源器件5、总结 无源器件是电子电路的主要构建模块,没有它们,这些电路要么根本无法工作,要么变得不稳定。 1、概述 那么什么是…...
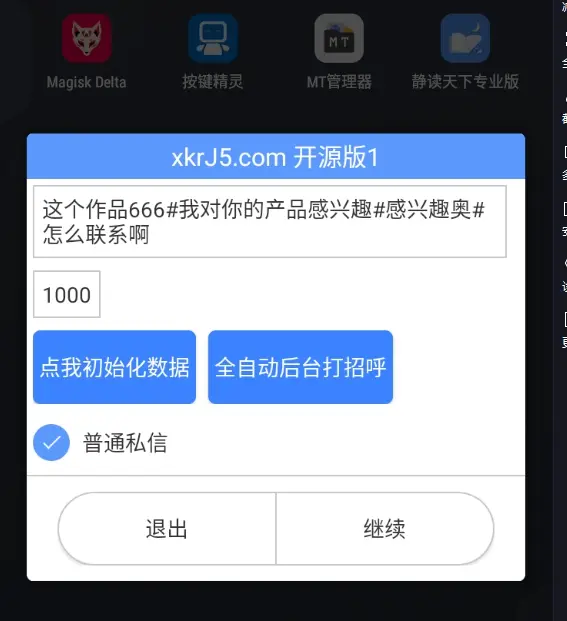
拼多多商家私信群发脚本,按键精灵版工具,源码分享
也是用按键精灵写的,实现的功能就是通过图色识别拼多多商品列表然后逐个对商家客服进行私信,私信内容可以在脚本里面提前配置好,代码怎么部署?回答:粘贴到你的按键精灵就行了,因为代码完全开源。 UI界面&a…...

在原生HTML页面发起axios请求
在原生html页面发起axios请求,首先需要先引入axios文件包,然后按照axios的请求方式发起请求即可,但如果页面在本地,那么请求一般会报错跨域问题,需要部署一下才能正确请求数据; 例子 <!DOCTYPE html&g…...

重看工厂模式
重看工厂模式 之前整个设计模式的专栏是看了李建忠老师的视频,并没有太多的自己的总结,今天来回看一下设计模式,重温设计模式的魅力 工厂模式我们介绍三个: 简单工厂 工厂方法 抽象工厂 简单工厂 我们举个例子,…...
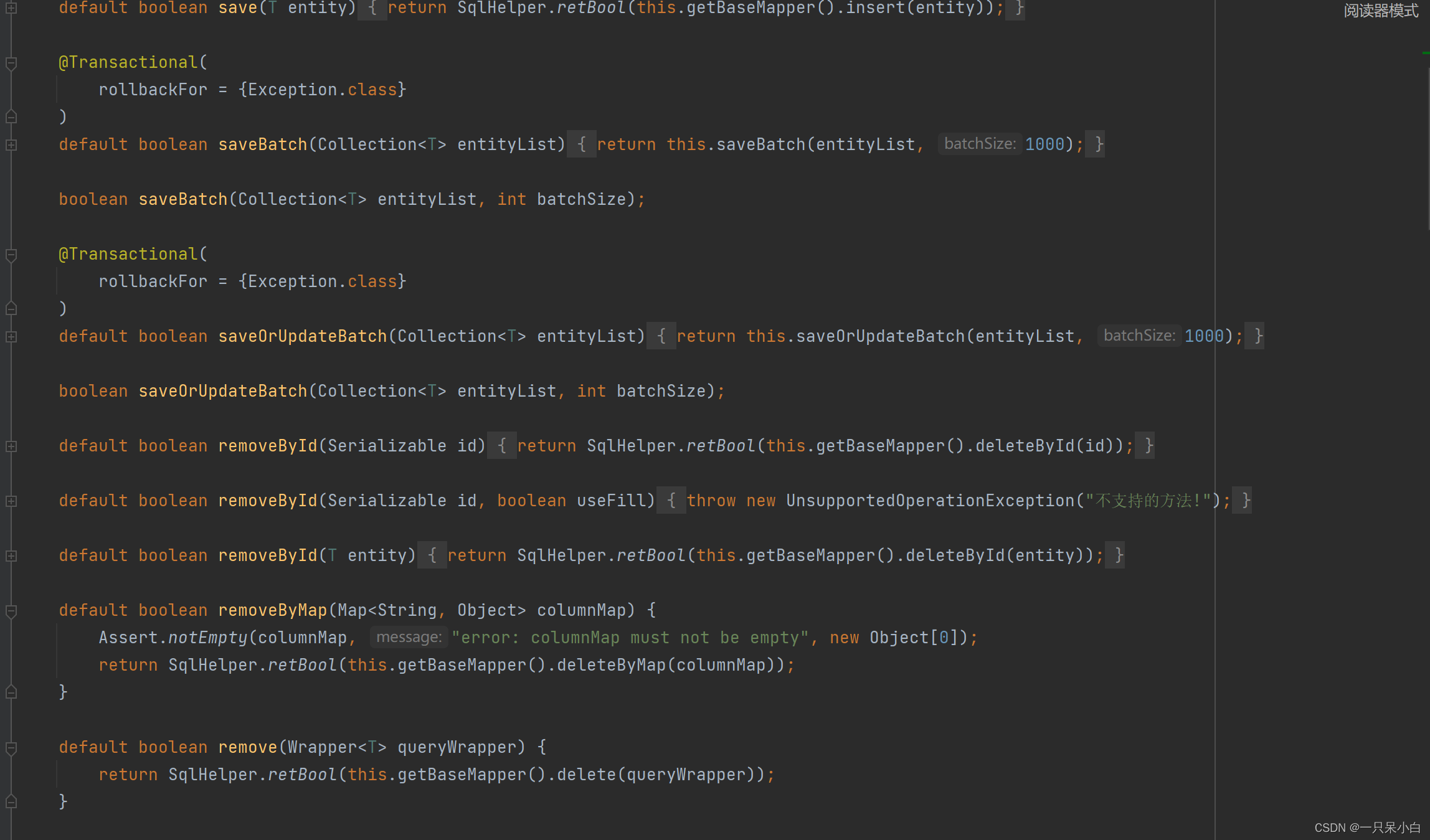
基于SpringBoot的SSMP整合案例(业务层基础开发与快速开发)
业务层基础开发 接口类public interface BookService {boolean save(Book book);boolean update(Book book);boolean delete(Integer id);Book getById(Integer id);List<Book> getAll();IPage<Book> getByPage(int currentPage,int pageSize);IPage<Book> …...

[Android]创建TabBar
创建一个包含“首页”、“分类”和“我的”选项卡的TabBar并实现切换功能,通常可以通过使用TabLayout结合ViewPager或ViewPager2来完成。以下是一个基本的示例,展示了如何使用Kotlin和XML来实现这个功能。 1.添加依赖项到build.gradle dependencies {/…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
