【算法与数据结构】前言
算法与数据结构是OI中不可或缺的一部分。
今天,让我们走进算法与数据结构独特世界。
性能
算法与数据结构都是完成任务的方法。
方法就要有性能。
有效率就有描述性能的语言。
这就是复杂度。
复杂度的描述
由于复杂度描述的是大致性能,所以采用的是近似的方法,将复杂度用一个函数和一个记号表示,记号称为渐进记号。
渐进记号有三种:(实际上有六种,在这里看,但一般只用这三种)
- f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n)),其中 f ( n ) , g ( n ) f(n),g(n) f(n),g(n) 为函数,下同
它表示 f ( n ) f(n) f(n) 在 g ( n ) g(n) g(n) 的两个常数倍之间。
形式化的, ∃ c 1 , c 2 , n 0 > 0 \exist c_1,c_2,n_0>0 ∃c1,c2,n0>0 使得 ∀ n ≥ n 0 \forall n\ge n_0 ∀n≥n0, 0 ≤ c 1 ⋅ g ( n ) ≤ f ( n ) ≤ c 2 ⋅ g ( n ) 0\le c_1\cdot g(n)\le f(n)\le c_2\cdot g(n) 0≤c1⋅g(n)≤f(n)≤c2⋅g(n) - f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n))
它表示 f ( n ) f(n) f(n) 在 g ( n ) g(n) g(n) 的某个常数倍以下。
形式化的, ∃ c , n 0 > 0 \exist c,n_0>0 ∃c,n0>0 使得 ∀ n ≥ n 0 \forall n\ge n_0 ∀n≥n0, 0 ≤ f ( n ) ≤ c ⋅ g ( n ) 0\le f(n)\le c\cdot g(n) 0≤f(n)≤c⋅g(n) - f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f(n)=Ω(g(n))
它表示 f ( n ) f(n) f(n) 在 g ( n ) g(n) g(n) 的某个常数倍以上。
形式化的, ∃ c , n 0 > 0 \exist c,n_0>0 ∃c,n0>0 使得 ∀ n ≥ n 0 \forall n\ge n_0 ∀n≥n0, 0 ≤ c ⋅ g ( n ) ≤ f ( n ) 0\le c\cdot g(n)\le f(n) 0≤c⋅g(n)≤f(n)
复杂度的计算简单来说如下:
- 舍去各项常数
- 舍去除最高次项外的其它项(若数据范围特殊可保留一定项)
- 余下的即为所求
对于OI来说,算法与数据结构需要达到一定的时间和空间性能,对应的,产生了时间复杂度和空间复杂度:
时间复杂度
时间复杂度是描述算法消耗时间的语言。
时间复杂度分为三种,最好时间复杂度,最坏时间复杂度,平均时间复杂度,顾名思义。
OI赛制下一般不考虑最好时间复杂度。
时间复杂度的计算
取某种情况,例如输入序列 a a a 按升序排序, ∀ n ≥ n 0 \forall n\ge n_0 ∀n≥n0,在该条件下,有执行次数始终为 n ( n + 1 ) 2 \frac{n(n+1)}2 2n(n+1),可以将这种情况下的时间复杂度表达为 n ( n + 1 ) 2 = Θ ( n 2 ) \frac{n(n+1)}2=\Theta(n^2) 2n(n+1)=Θ(n2)。
同理,我们可以在分析各种情况的基础下计算出三种时间复杂度,一般取平均时间复杂度和最坏时间复杂度来比较算法的速度。
空间复杂度
空间复杂度是描述算法消耗空间的语言。
空间复杂度直接定义对变量的数量计算即可。
空间复杂度非常简单,就不多说了。
N e x t : Next: Next:
算法前言
数据结构前言
相关文章:

【算法与数据结构】前言
算法与数据结构是OI中不可或缺的一部分。 今天,让我们走进算法与数据结构独特世界。 性能 算法与数据结构都是完成任务的方法。 方法就要有性能。 有效率就有描述性能的语言。 这就是复杂度。 复杂度的描述 由于复杂度描述的是大致性能,所以采用的是…...
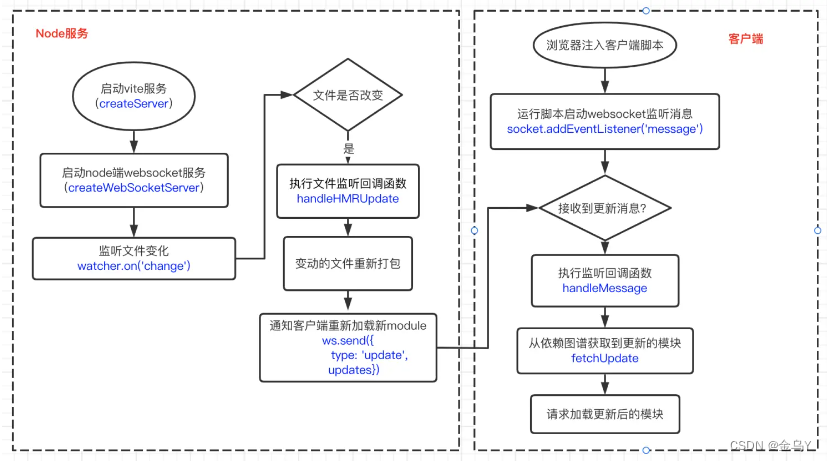
(六)什么是Vite——热更新时vite、webpack做了什么
vite分享ppt,感兴趣的可以下载: Vite分享、原理介绍ppt 什么是vite系列目录: (一)什么是Vite——vite介绍与使用-CSDN博客 (二)什么是Vite——Vite 和 Webpack 区别࿰…...
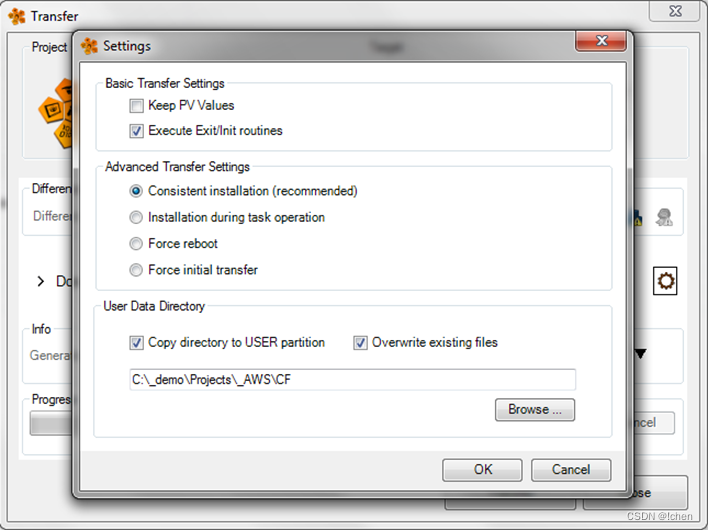
贝加莱MQTT功能
贝加莱实现MQTT Client端的功能库和例程 导入库和例程,AS Logical View中分别通过Add Object—Library,Add—Program插入MQTT库和例程。 将例程Sample放置于CPU循环周期中 定义证书存放路径,在AS Physical View 中,右击PLC—Con…...

基于JavaWeb+SSM+购物系统微信小程序的设计和实现
基于JavaWebSSM购物系统微信小程序的设计和实现 源码获取入口前言主要技术系统设计功能截图Lun文目录订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码获取入口 前言 第一章 绪 论 1.1选题背景 互联网是人类的基本需求,特别是在现代社会,…...

为什么需要Code Review?
1. Code Review 是什么? 代码审查(Code Review)是软件开发过程中对代码进行系统性检查和评审的一项活动。它是指团队成员之间相互检查彼此编写的代码,以确保代码质量、可读性和符合编码标准等。 2. Code Review 的必要性 ● 提…...
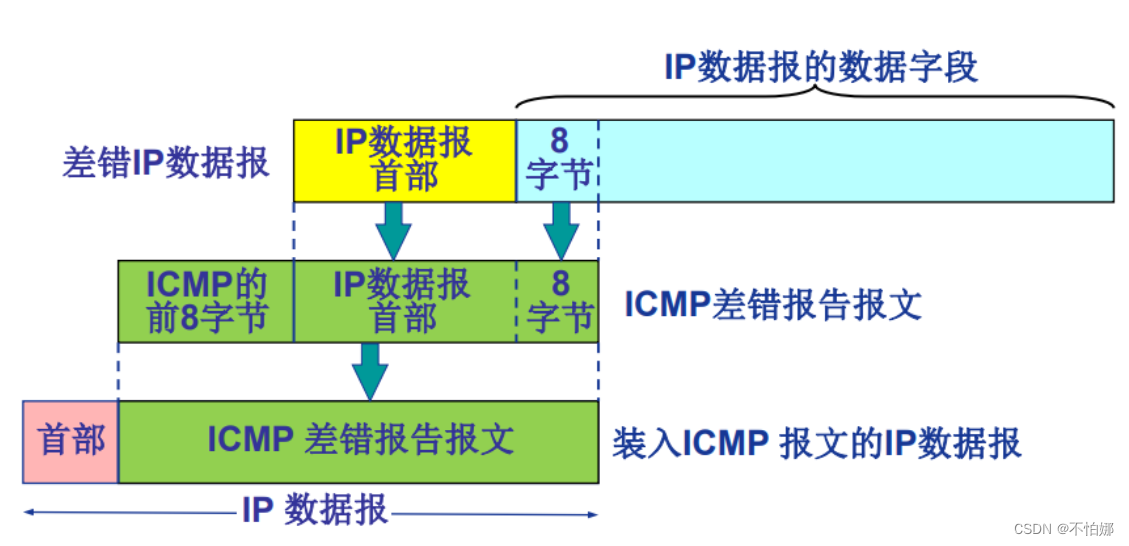
【计算机网络笔记】ICMP(互联网控制报文协议)
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

Git教程1:生成和提交SSH公钥到远程仓库
要生成 Git 的公钥并将其提交到远程仓库,你可以按照以下步骤进行操作: 打开命令行终端,并确保已经安装了 Git。在终端中输入以下命令来生成 SSH 密钥对:ssh-keygen -t rsa -b 4096 -C "your_emailexample.com"这将生成…...
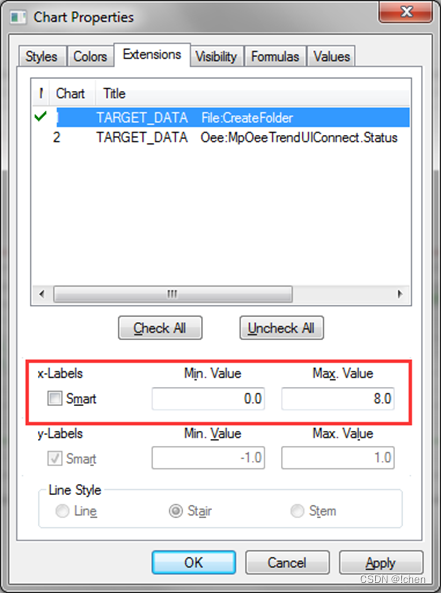
贝茄莱BR AS实时数据采集功能
实时数据采集功能在PLC系统调试过程中,有助于调试人员对变量变化进行监测,通过波形对比,反应不同变量间的相互作用。该测试目的在于验证贝加莱系统组态软件的实时数据采集功能。 贝加莱系统组态软件提供Trace功能,连接PLC&#x…...
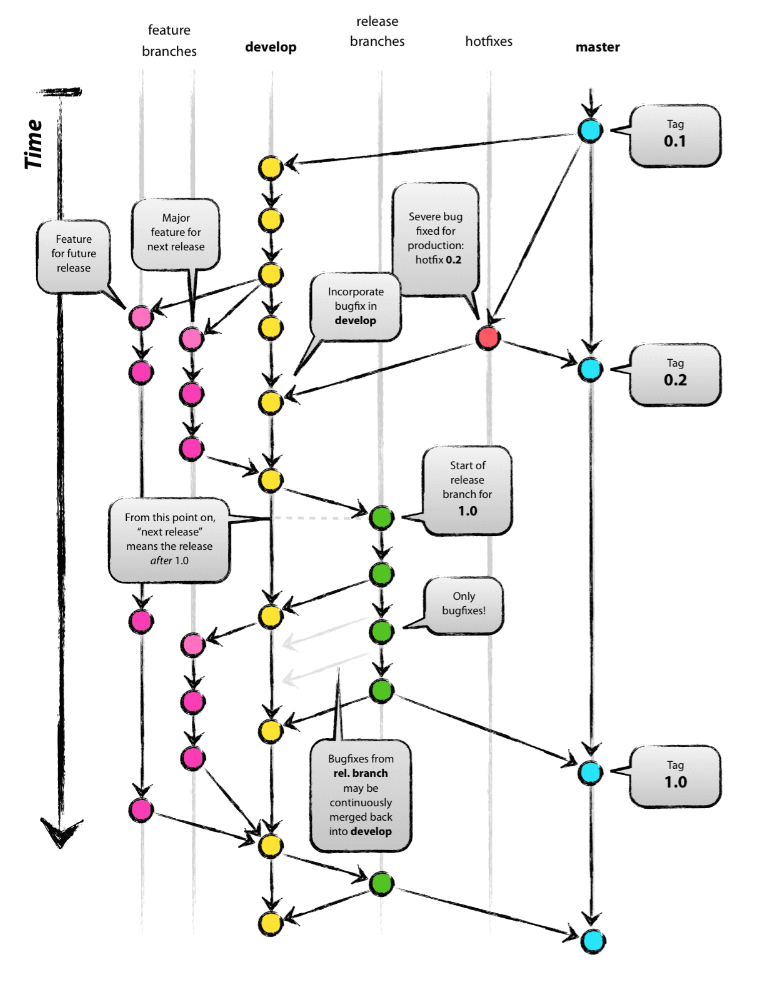
Git的基本操作以及原理介绍
文章目录 基本操作创建git仓库配置name和email .git目录的结构git add & git commit.git目录结构的变化 git追踪管理的数据git的版本回退回退的原理回退的三种情况 版本库中文件的删除git分支管理分支的删除合并分支时的冲突分支的合并模式分支策略git stash不要在master分…...

2023安全与软工顶会/刊中区块链智能合约相关论文
2023安全与软工顶会/刊中区块链智能合约相关论文 前言软工顶会ISSTAFSEASEICSE 软工顶刊TOSEMTSE 安全顶会S&PUSENIX SecurityCCSNDSS 前言 主要整理了2023年四大安全顶会、四大软工顶会和两个软工顶刊中,有关区块链智能合约的相关论文。 搜索方式是࿱…...
word文档转换为ppt文件,怎么做?
大家是否会遇到需要将word文档转换为ppt文件的情况?除了反反复复粘贴复制以外,还有其他方法可以转换文件格式,今天给大家分享word转换ppt方法。 首先我们先将word文件打开大纲模式 然后我们将文中的大标题设置为1级标题,副标题设…...

机器视觉选型-什么时候用远心镜头
物体厚 当被检测物体厚度较大,需要检测不止一个平面时,典型应用如食品盒,饮料瓶等。 物体位置变化 当被测物体的摆放位置不确定,可能跟镜头成一定角度时。 物体上下跳动 当被测物体在被检测过程中上下跳动,如生产线上下…...
quartz笔记
Quartz-CSDN博客 上面是Quartz的一些基本知识,如果对quartz的基本API不是很了解的话,建议先看下上面的 和Linux Crontab对比 1.执行粒度: Linux Crontab是进程级 quart是线程级 2.跨平台性: Crontab只能在Linxu运行 quart是java实现,可以跨平台 3.调度集上 Crontab的…...
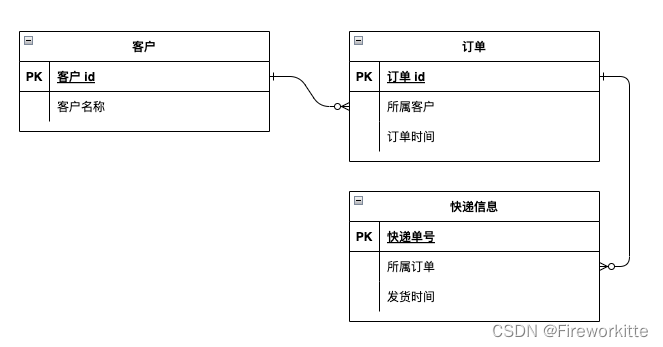
ER 图是什么
文章目录 前言什么是 ER图ER 图实例简化的 ER 图总结 前言 产品经理在梳理产业业务逻辑的过程中,非常重要的一项工作就是梳理各个业务对象之间的关系。如果涉及对象很对的时候,没有工具支持的话很难处理清楚。今天我们就来介绍一个梳理业务对象关系的工…...
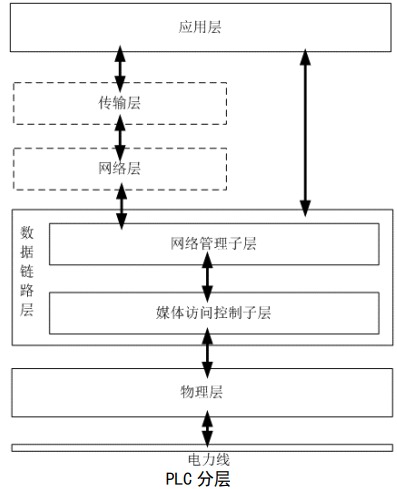
PLC电力载波通讯,一种新的IoT通讯技术
前言: PLC-IoT 是 PLC 技术应用在物联场景的创新实践,有效解决电力线路信号干扰、衰减问题,支持 IP 化通信能力,使能终端设备智能化,构建智慧边缘联接。PLC让传统IoT有了更多的连接可能: 电力线通信技术适用的场景包括电力配用电网络、城市智慧路灯、交通路口信号灯、园…...

Elasticsearch:通过摄取管道加上嵌套向量对大型文档进行分块轻松地实现段落搜索
作者:VECTOR SEARCH 向量搜索是一种基于含义而不是精确或不精确的 token 匹配技术来搜索数据的强大方法。 然而,强大的向量搜索的文本嵌入模型只能按几个句子的顺序处理短文本段落,而不是可以处理任意大量文本的基于 BM25 的技术。 现在&…...
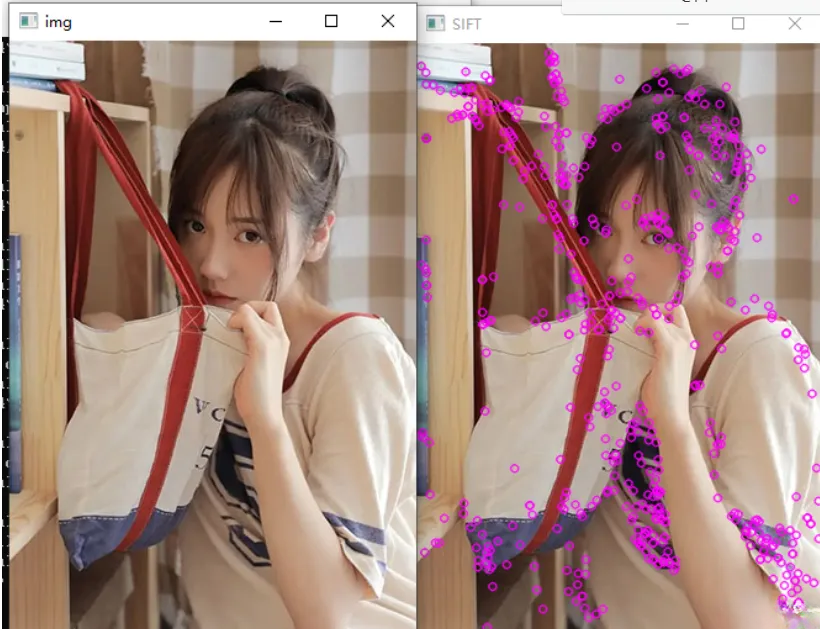
OpenCV图像纹理
LBP描述 LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikinen, 和D. Harwood 在1994年提出,用于纹理特征提取…...

自媒体写手提问常用的ChatGPT通用提示词模板
如何撰写一篇具有吸引力和可读性的自媒体文章? 如何确定自媒体文章的主题和受众群体? 如何为自媒体文章取一个引人入胜的标题? 如何让自媒体文章的开头更加吸引人? 如何为自媒体文章构建一个清晰、逻辑严谨的框架?…...

分类预测 | Matlab实现PSO-LSTM-Attention粒子群算法优化长短期记忆神经网络融合注意力机制多特征分类预测
分类预测 | Matlab实现PSO-LSTM-Attention粒子群算法优化长短期记忆神经网络融合注意力机制多特征分类预测 目录 分类预测 | Matlab实现PSO-LSTM-Attention粒子群算法优化长短期记忆神经网络融合注意力机制多特征分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1…...
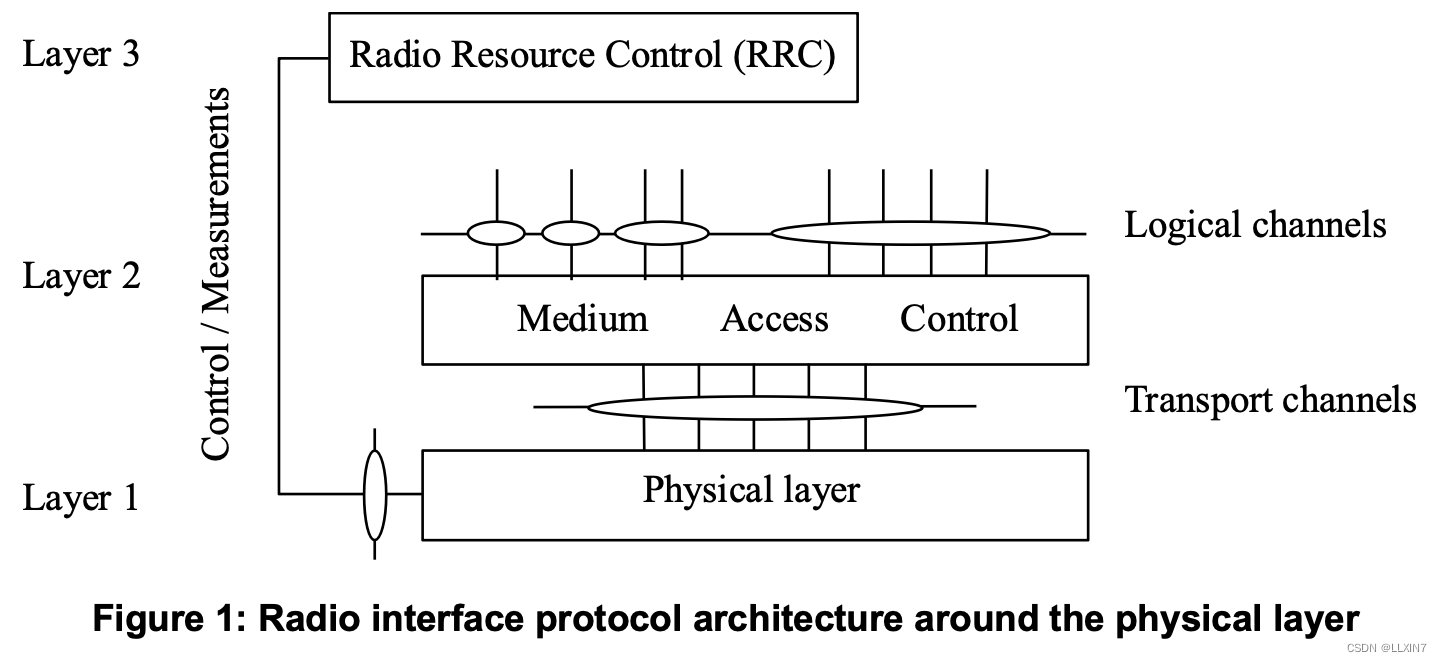
3GPP TS38.201 NR; Physical layer; General description (Release 18)
TS38.201是介绍性的标准,简单介绍了RAN的信道组成和PHY层承担的功能,下图是PHY层相关标准的关系。 文章目录 结构信道类型调制方式PHY层支持的过程物理层测量其他标准TS 38.202: Physical layer services provided by the physical layerTS 38.211: Ph…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
