【PTA题目】6-20 使用函数判断完全平方数 分数 10
6-20 使用函数判断完全平方数
分数 10
全屏浏览题目
切换布局
作者 张高燕
单位 浙大城市学院
本题要求实现一个判断整数是否为完全平方数的简单函数。
函数接口定义:
int IsSquare( int n );其中n是用户传入的参数,在长整型范围内。如果n是完全平方数,则函数IsSquare必须返回1,否则返回0。
裁判测试程序样例:
#include <stdio.h>
#include <math.h>int IsSquare( int n );int main()
{int n;scanf("%d", &n);if ( IsSquare(n) ) printf("YES\n");else printf("NO\n");return 0;
}/* 你的代码将被嵌在这里 */输入样例1:
90输出样例1:
NO输入样例2:
100
输出样例2:
YES
鸣谢安阳师范学院段晓云老师、用户黄凯涵修正数据~
代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB
参考答案
int IsSquare( int n ){for(int i=1;i<=n;i++){if(n/i==i)return 1;}if(n==0)return 1;return 0;
}相关文章:

【PTA题目】6-20 使用函数判断完全平方数 分数 10
6-20 使用函数判断完全平方数 分数 10 全屏浏览题目 切换布局 作者 张高燕 单位 浙大城市学院 本题要求实现一个判断整数是否为完全平方数的简单函数。 函数接口定义: int IsSquare( int n ); 其中n是用户传入的参数,在长整型范围内。如果n是完全…...
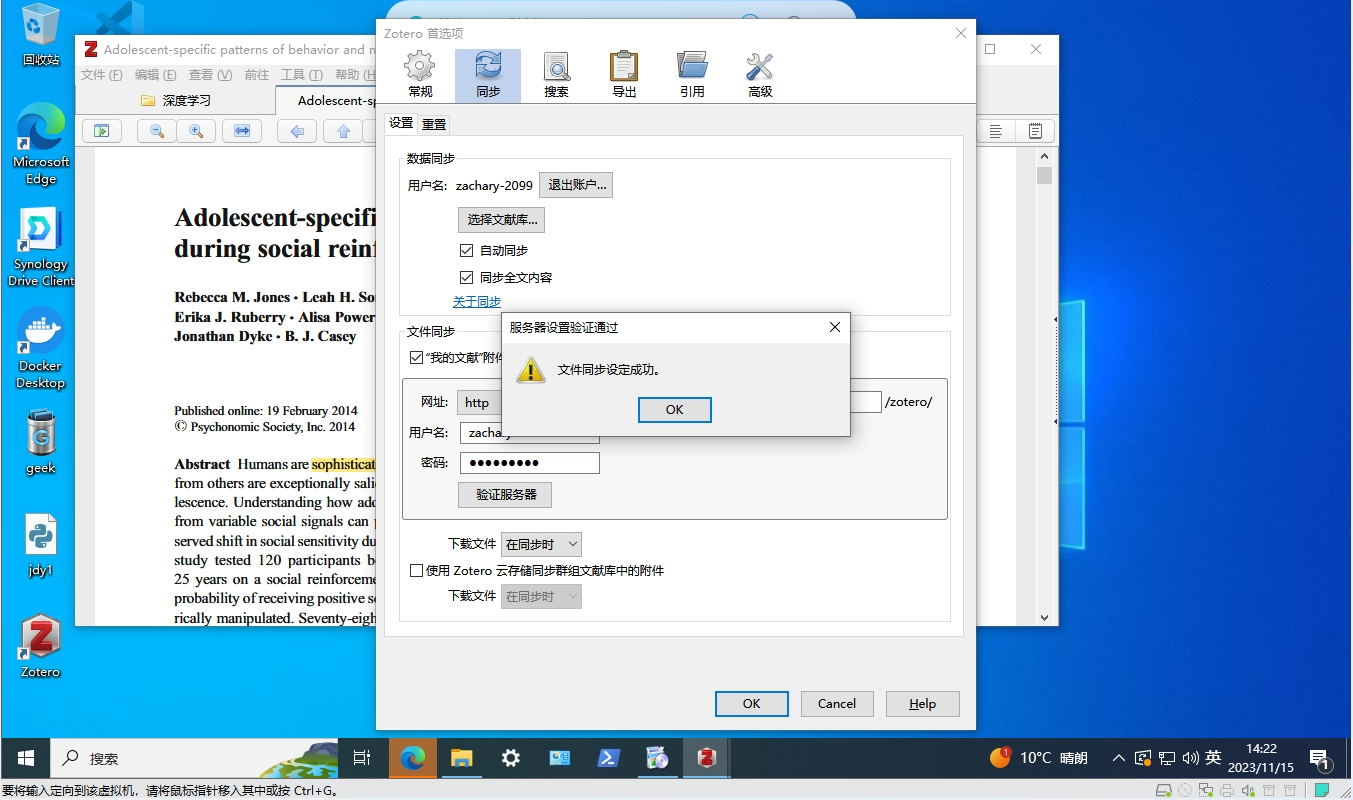
Nas搭建webdav服务器并同步Zotero科研文献
无需云盘,不限流量实现Zotero跨平台同步:内网穿透私有WebDAV服务器 文章目录 无需云盘,不限流量实现Zotero跨平台同步:内网穿透私有WebDAV服务器一、Zotero安装教程二、群晖NAS WebDAV设置三、Zotero设置四、使用公网地址同步Zote…...

一句话总结敏捷实践中不同方法
敏捷实践是指一组优先考虑灵活性、协作和客户满意度的软件开发和项目管理原则和方法。 不同方法论的敏捷实践: 1、敏捷: Sprints:限时迭代(通常 2-4 周),在此期间创建潜在的可交付产品增量。每日站立会议…...

【数据结构】线段树(点修区查)
数据结构-线段树(点修区查) 前置知识 分治递归二叉树 思路 我们需要维护一个支持单点修改,区间查询的数据结构,并且要求在线,一般使用线段树解决。 线段树是一个二叉树形的数据结构。 线段树的思想很简单,…...
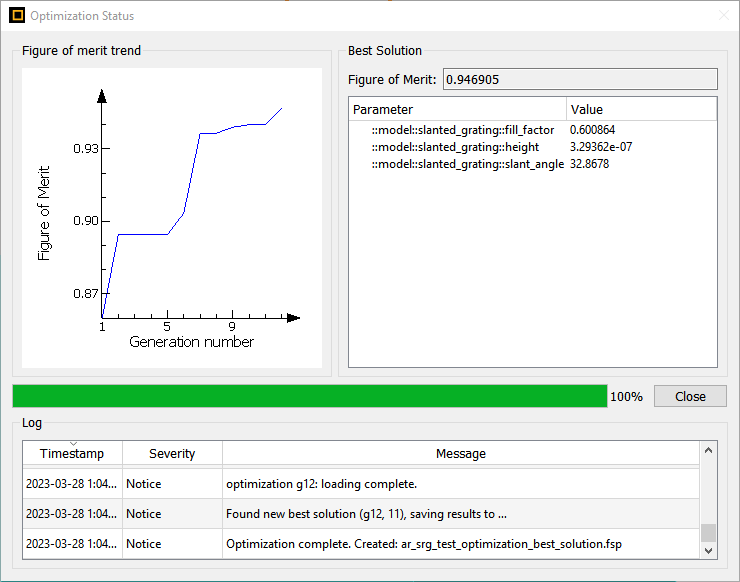
Ansys Lumerical | 用于增强现实系统的表面浮雕光栅
在本示例中,我们使用 RCWA 求解器设计了一个斜面浮雕光栅 (SRG),它将用于将光线耦合到单色增强现实 (AR) 系统的波导中。光栅的几何形状经过优化,可将正常入射光导入-1 光栅阶次。 然后我们将光栅特性导出为 Lumerical Sub-Wavelength Model …...

QT day3作业
1.思维导图 2、 完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到其他界面 如果账号和密…...
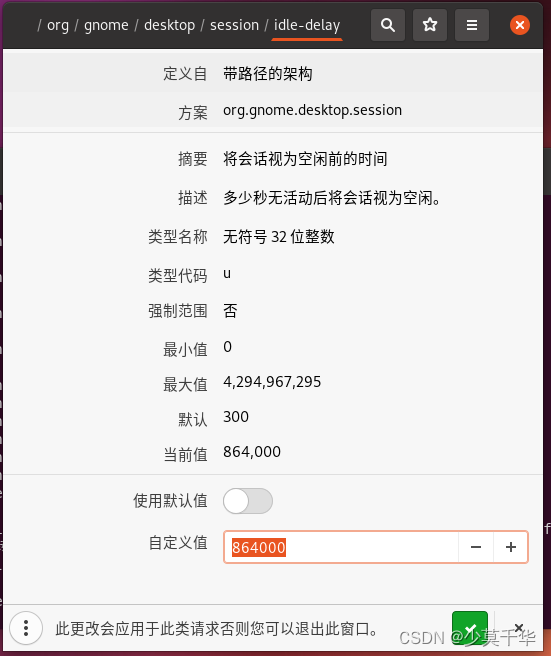
【Ubuntu】设置永不息屏与安装 dconf-editor
方式一、GUI界面进行设置 No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 20.04.6 LTS Release: 20.04 Codename: focal打开 Ubuntu 桌面环境的设置菜单。你可以通过点击屏幕右上角的系统菜单,然后选择设置。在设置菜单中,…...
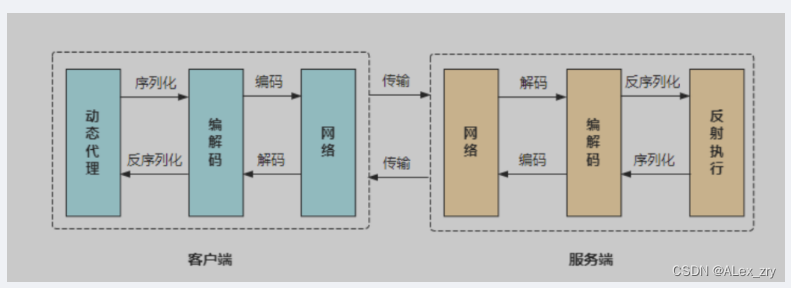
gRPC 的原理 介绍带你从头了解gRPC
gRPC 的原理 什么是gRPC gRPC的官方介绍是:gRPC是一个现代的、高性能、开源的和语言无关的通用 RPC 框架,基于 HTTP2 协议设计,序列化使用PB(Protocol Buffer),PB 是一种语言无关的高性能序列化框架,基于 HTTP2PB 保…...
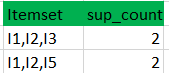
Apriori算法
Apriori算法由R. Agrawal和R. Srikant于1994年在数据集中寻找布尔关联规则的频繁项集。该算法的名称是Apriori,因为它使用了频繁项集属性的先验知识。我们应用迭代方法或逐层搜索,其中k-频繁项集用于找到k1个项集。 为了提高频繁项集逐层生成的效率&…...

肖sir__linux讲解(2.1)
linux命令 cp 复制命令 a、cp 原文件名称 新文 件名称(不存在的文件) 案例:cp a k 截图: b.cp 原文件名称 原有文 件名称(存在的文件) 案例:cp a b 截图: c、cp 指定路径复制 格式ÿ…...

The ultimate UI kit and design system for Figma 组件库下载
Untitled UI 是世界上最大的 Figma UI 套件和设计系统。可以启动任何项目,为您节省数千小时,并祝您升级为专业设计师。 采用 100% 自动布局 5.0、变量、智能变体和 WCAG 可访问性精心制作。 900全局样式、变量:超级智能的全局颜色、排版和效…...

Selenium——利用input标签上传文件
Selenium利用input标签上传文件 完整流程 打开文件上传页面选择要上传的文件点击上传按钮确认文件上传成功介绍怎么方便的获取对应元素的Xpath或者Css 简单介绍 在使用Selenium进行浏览器自动化测试时,文件上传是一个常见的需求。而 标签就是实现文件上传功能的…...
C++初阶 日期类的实现(下)
目录 一、输入输出(>>,<<)重载的实现 1.1初始版 1.2友元并修改 1.2.1简单介绍下友元 1.2.2修改 1.3>>重载 二、条件判断操作符的实现 2.1操作符的实现 2.2!操作符的实现 2.3>操作符的实现 2.4>,<,<操作符的实现 三、日期-日期的实现 …...

大师学SwiftUI第16章 - UIKit框架集成
其它相关内容请见虚拟现实(VR)/增强现实(AR)&visionOS开发学习笔记 SwiftUI是一套新框架,因此并没有包含我们构建专业应用所需的所有工具。这意味着我们会需要求助于UIKit(移动设备)和AppKit(Mac电脑)等原…...
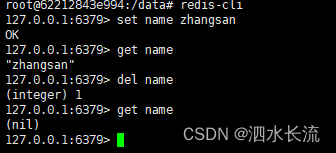
7.docker运行redis容器
1.准备redis的配置文件 从上一篇运行MySQL容器我们知道,需要给容器挂载数据卷,来持久化数据和配置,相应的redis也不例外。这里我们以redis6.0.8为例来实际说明下。 1.1 查找redis的配置文件redis.conf 下面这个网址有各种版本的配置文件供…...

unity教程
前言 伴随游戏行业的兴起,unity引擎的使用越来越普遍,本文章主要记录博主本人入门unity的相关记录大部分依赖siki学院进行整理。12 一、认识unity引擎? 1、Unity相关信息: Unity的诞生:https://www.jianshu.com/p/550…...

未定义与 ‘double‘ 类型的输入参数相对应的函数 ‘Link‘
报错 检查对函数"Link"得调用中是否缺失参数或参数数据类型不正确。 未定义与"double"类型的输入参数相对应的函数"Link"。 问题描述 网上搜了搜一般说是toolbox没有下载导致的,相当于调用的包本地没有。 但是我看看了 Robotics…...

为什么Transformer模型中使用Layer Normalization(Layer Norm)而不是Batch Normalization(BN)
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
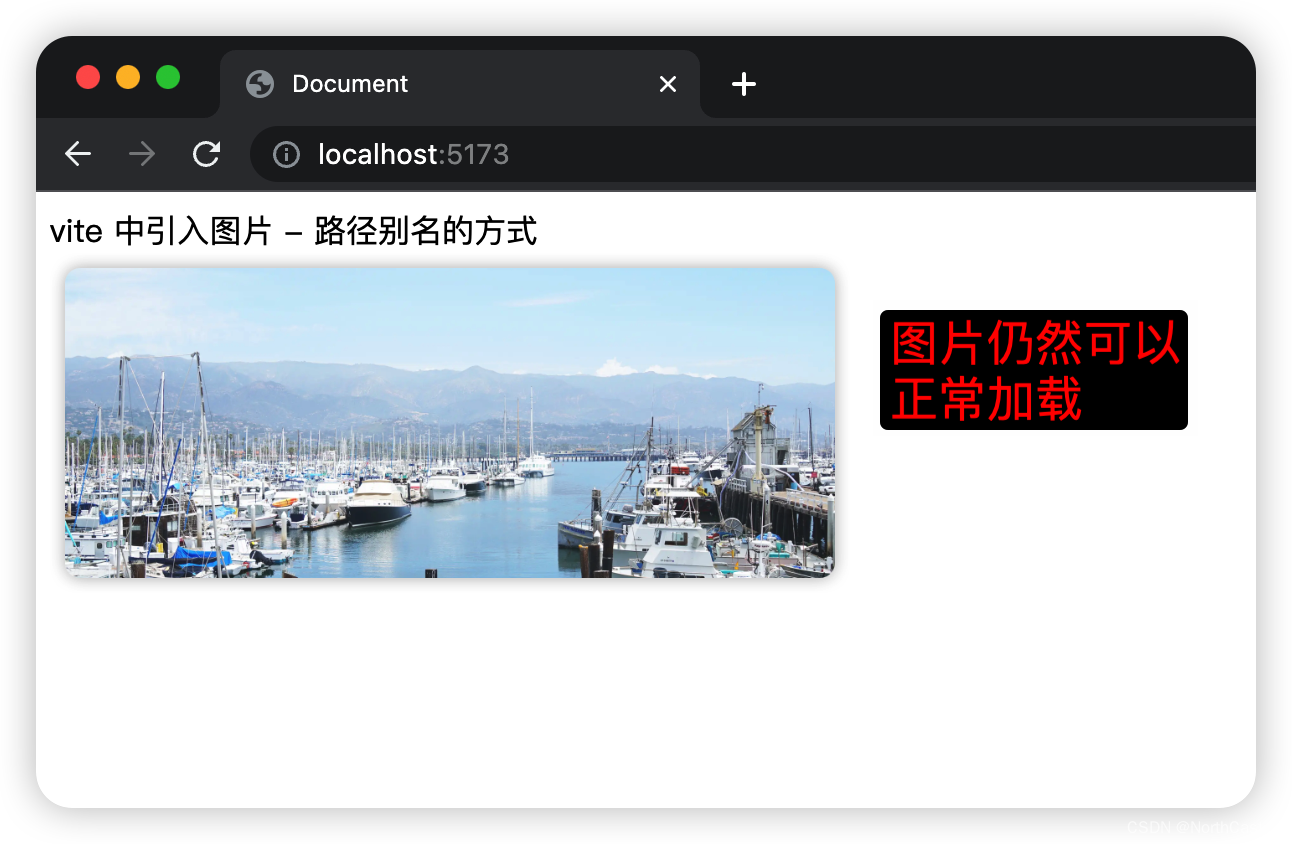
Vite - 配置 - 文件路径别名的配置
为什么要配置别名 别名的配置,主要作用是为了缩短代码中的导入路径。例如有如下的项目目录: project-name| -- src| -- a| --b| --c| --d| --e| -- abc.png| -- index.html| -- main.js如果想在 main.js 文件中使用 abc.png ,则使用的路径是 ࿱…...

phpStorm Xdebug调试 加FireFox浏览器
步骤1: [Xdebug] zend_extension“D:\phpstudy_pro\Extensions\php\php5.4.45nts\ext\php_xdebug.dll” xdebug.collect_params1 xdebug.collect_return1 xdebug.remote_enableOn xdebug.remote_hostlocalhost xdebug.remote_port9001 xdebug.remote_handlerdbgp ;…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
