数学小课堂:无穷小(以动态的眼光看待世界,理解无限的世界)
文章目录
- 引言
- I 芝诺四个著名的悖论
- 1.1 二分法悖论:从A点到B点是不可能的。
- 1.2 阿喀琉斯悖论:阿喀琉斯追不上乌龟。
- 1.3 飞箭不动悖论:射出去的箭是静止的。
- 1.4 基本空间和相对运动悖论
- II 回答芝诺的悖论
- 2.1 阿喀琉斯悖论
- 2.2 相对运动悖论
- III 无穷小
- 3.1 无穷小的定义
- 3.1 无穷小的本质
- 3.2 案例:弦论
引言
无穷小并不是一个确定的数,更不是零,它和无穷大一样,是一种趋势,一种帮助我们把握“动态”和“变化”的工具,也是一种新的认知世界的方式。
I 芝诺四个著名的悖论
严守逻辑的思维方式,才让数学和自然科学成体系地发展。
看似正确的逻辑,本身可能有问题,因为有概念的缺失,芝诺的这第三和第四个悖论就属于
相关文章:
)
数学小课堂:无穷小(以动态的眼光看待世界,理解无限的世界)
文章目录 引言I 芝诺四个著名的悖论1.1 二分法悖论:从A点到B点是不可能的。1.2 阿喀琉斯悖论:阿喀琉斯追不上乌龟。1.3 飞箭不动悖论:射出去的箭是静止的。1.4 基本空间和相对运动悖论II 回答芝诺的悖论2.1 阿喀琉斯悖论2.2 相对运动悖论III 无穷小3.1 无穷小的定义3.1 无穷…...
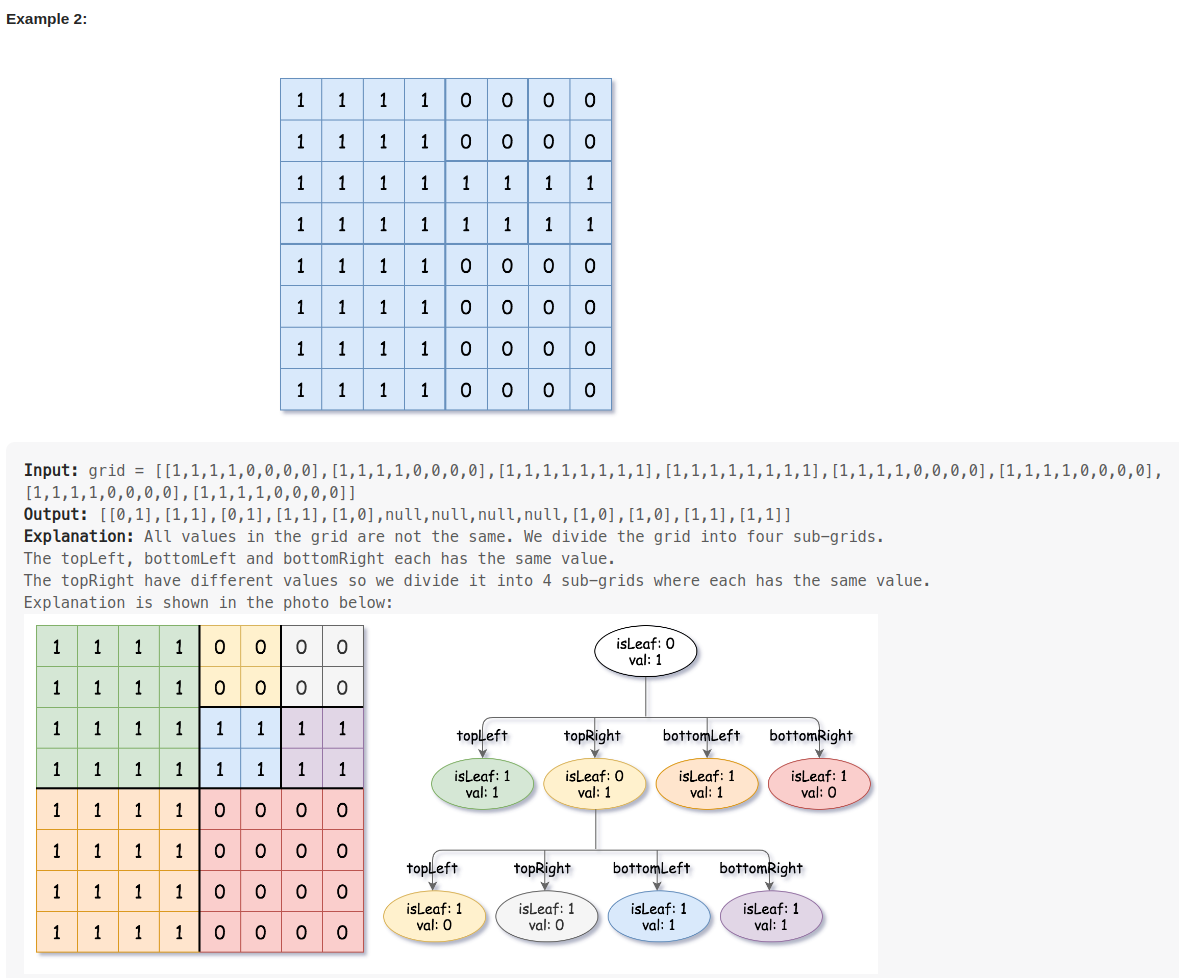
leetcode 427. Construct Quad Tree(构建四叉树)
刚看到题的时候是懵的,这也太长了。到底是要表达什么呢。 不妨把这个矩阵看成一个正方形的图片,想象你在处理图片,从整体逐步到局部。 刚开始看一整张图片,如果是全0或全1,这个就是叶子节点,怎么表达叶子节…...
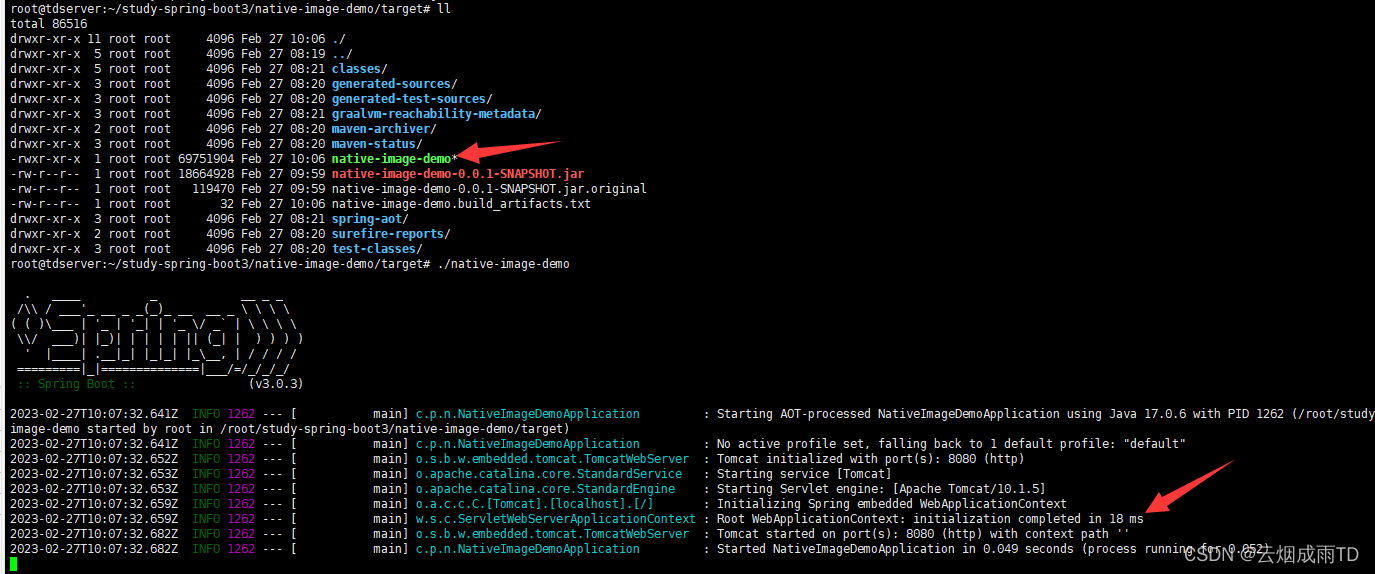
Spring Boot 3.0系列【2】部署篇之使用GraalVM构建原生镜像
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本2.7.0 文章目录概述JIT & AOTJIT (动态编译)AOT(静态编译)GraalVM简介运行模式Native Image(原生镜像)…...
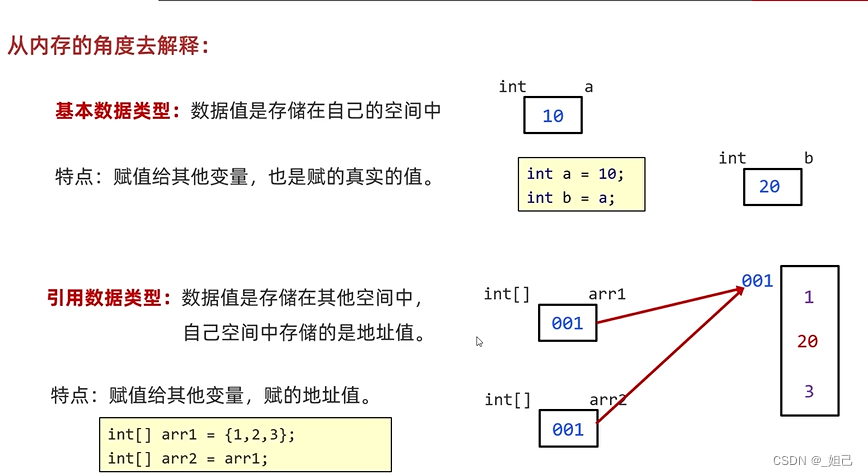
复习知识点十之方法的重载
目录 方法的重载 练习1: 练习1: 数组遍历 练习2: 数组的最大值 练习3: 练习4: 复制数组 基本数据类型和引用数据类型 方法的重载 Java虚拟机会通过参数的不同来区分同名的方法 练习1: public class Test4 {public static void main(String[] args) {//调用方法 // …...

火爆全网的ChatGPT 和AI 可以为项目经理做什么?
作为一款人工智能聊天机器人,ChatGPT因其逼真和人性化的特性而风靡全球,无疑是当今技术的新流行。人工智能 (AI) 有可能彻底改变许多行业,包括项目管理,及时了解最新技术以及它如何影响你的工作至关重要。于是,我们与C…...

前端面试题 —— HTML
目录 一、src 和 href 的区别 二、对 HTML 语义化的理解 三、DOCTYPE(⽂档类型) 的作⽤ 四、script 标签中 defer 和 async 的区别 五、常⽤的 meta 标签有哪些? 六、HTML5 有哪些更新 八、行内元素有哪些?块级元素有哪些? 空(void)元素…...

同为(TOWE)电源线让家用电器随心放置
如今,随着科技水平的不断发展,人们工作、生活中越来越离不开各类电子设备和电器产品。当用电器数量多了以后,由于电器设备原有电线长度的限制,常常需要通过连接接线板来延长电器设备的电能传输线路。电源线虽然看着是一件不起眼的…...
)
2023上半年数学建模竞赛汇总(报名时间、比赛时间、难易程度、含金量、竞赛官网)
1、美国大学生数学建模竞赛等级:国家级是否可跨校:否竞赛开始时间:2月17日~2月21日综合难度:⭐⭐⭐⭐ 竞赛含金量:⭐⭐⭐⭐⭐竞赛官网:https://www.comap.com/2、MathorCup高校数学建模挑战赛---大数据竞赛…...

RK3568平台开发系列讲解(驱动基础篇)SMP(Symmetrical Multi-Processing)
🚀返回专栏总目录 文章目录 一、linux SMP 和 AMP二、linux SMP的启动流程三、CPU的描述:cpumask四、CPU之间的关系沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将介绍 SMP(Symmetrical Multi-Processing)。 一、linux SMP 和 AMP 目前支持多核处理器的实时操…...

HIVE --- zeppelin安装
目录 把zeppelin压缩包拷贝到虚拟机里面 解压 改名 修改配置文件 编辑zeppelin-site.xml—将配置文件的ip地址和端口号进行修改 编辑 zeppelin-env.sh—添加JDK和Hadoop环境 配置环境变量 刷新环境变量 拷贝Hive文件 拷贝外部文件 启动zeppelin 启动Hadoop&Hi…...

数据分析中的变量解释
1.数值变量Numerical Variables 数值型变量(metric variable)是说明事物数字特征的一个名称,其取值是数值型数据。如“产品产量”、“商品销售额”、“零件尺寸”、“年龄”、“时间”等都是数值型变量,这些变量可以取不同的数值…...

django-博客(一)
一、 1、环境:pycharm,python3.6,django3,mysql8.0 2、创建项目 3、把html和css样式那些导入到文件夹中,然后配置这些文件夹的路径,再添加首页视图。 改成反向解析 python manage.py runserv…...
Shell高级——Linux中的文件描述符
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 前言 Linux中一切接文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上…...

洗地机哪个品牌最好用?家用洗地机十大名牌
这几年清洁类的小家电非常热门,无线吸尘器、扫地机器人、扫拖一体机、洗地机和擦窗机器人层出不穷,各个品牌百花齐放。这些清洁电器,确实为家庭卫生清洁带来了很大的便捷。但要把这些产品一次性买齐是一笔不小的开销,而且需要收纳…...
线程休眠)
java多线程(十)线程休眠
一、sleep()介绍 sleep() 定义在Thread.java中。 sleep() 的作用是让当前线程休眠,即当前线程会从“运行状态”进入到“休眠(阻塞)状态”。sleep()会指定休眠时间,线程休眠的时间会大于/等于该休眠时间;在线程重新被唤醒时,它会由…...

Leetcode20. 有效的括号
一、题目描述: 给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确…...
Android 项目必备(四十三)-->Android 开发者的 new 电脑
前言 作为 Android 开发者,当你新入职一家公司,拿到新发的电脑,你会对电脑干点啥? 安装开发环境?装软件?你是否还会铺天盖地到处找之前电脑备份的东西?又或者还想不起来有什么上一台电脑好用的…...

如何水平和垂直居中元素
跳到主内容 我试图将我的选项卡内容垂直居中,但是当我添加 CSS 样式时display:inline-flex,水平文本对齐消失了。 如何为每个选项卡同时对齐文本 x 和 y? * { box-sizing: border-box; } #leftFrame {background-color: green;position: a…...

Rust泛型Generics
泛型 泛型(Generics)是一种程序设计风格,它允许程序员在强类型语言(例如rust,c#,c)中编写代码时使用通用类型。以rust为例,如果你想实现一个通用的add函数,让其在u8, i3…...
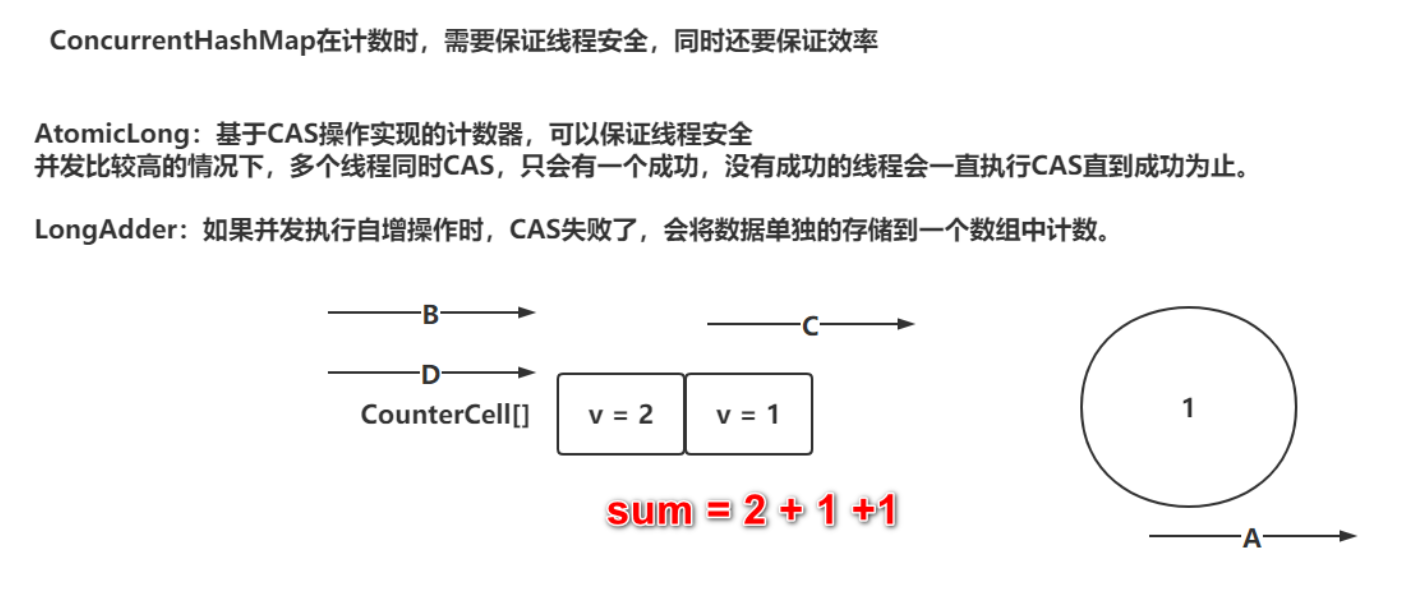
六、并发集合
文章目录并发集合ConcurrentHashMap存储结构存储操作put方法putVal方法-散列算法putVal方法-添加数据到数组&初始化数组putVal方法-添加数据到链表扩容操作treeifyBin方法触发扩容tryPreSize方法-针对putAll的初始化操作tryPreSize方法-计算扩容戳并且查看BUGtryPreSize方法…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
